Поиск кратчайших путей в графе. Алгоритм Дейкстры. Алгоритм Флойда

1.

Поиск кратчайших
путей в графе
Алгоритм Дейкстры
Алгоритм Флойда

2.

2
Большое количество практических задач формулируются как
задачи поиска фрагментов графа или каких-то его
характеристик, причем существует множество вариантов
решения.
Каждое решение оценивается числом. Среди множества решений
нужно найти такое, для которого оценка имеет экстремальное
значение –
минимальное
максимальное.
Чаще всего в качестве оценок используется сумма весов дуг или
ребер, входящих в решение.

3.

Задачи поиска путей
Пусть в графе заданы две вершины aн и aк, названные соответственно
начальной и конечной.
Выделим несколько задач, связанных с поиском путей в графе:
найти путь между начальной и конечной вершиной (эта задача
называется задачей поиска пути в лабиринте);
найти минимальный путь между заданными вершинами;
найти максимальный путь;
найти цикл Эйлера;
найти цикл Гамильтона.

4.

Кратчайший путь
Рассмотрим задачу поиска минимального пути между двумя заданными вершинами aн и aк в
графе при условии, что
каждой дуге (i, j) сопоставлен вес ci,j – неотрицательное число, задающее длину дуги,
и в качестве оценок путей используется сумма весов дуг.
Эта задача формулируется как задача нахождения кратчайшего пути
между заданными вершинами.
Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого
графом.
Существуют три наиболее эффективных алгоритма нахождения кратчайшего пути:
алгоритм Дейкстры (используется для нахождения оптимального маршрута между двумя
вершинами);
алгоритм Флойда (для нахождения оптимального маршрута между всеми парами вершин);
алгоритм Йена (для нахождения k-оптимальных маршрутов между двумя вершинами).
Указанные алгоритмы легко выполняются при малом количестве вершин в графе. При увеличении
их количества задача поиска кратчайшего пути усложняется. Здесь на помощь приходит современная
техника

5.

6.

Кратчайший путь: алгоритм Дейкстры
Алгори́тм Де́йкстры (англ. Dijkstra’s algorithm) — алгоритм на графах,
изобретённый нидерландским ученым Э. Дейкстрой в 1959 году.
Находит кратчайшее расстояние от одной из вершин графа до всех
остальных.
Алгоритм работает только для графов без рёбер отрицательного веса.
Тезис Дейкстры:
если кратчайший путь проходит через вершину ai, то длина части пути
от aн до ai должна быть минимально возможной.
Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой
вершины до a.
Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается
уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

7.

Кратчайший путь: алгоритм Дейкстры
Инициализация. Метка самой вершины a полагается равной 0, метки остальных
вершин — бесконечности. Это отражает то, что расстояния от a до других вершин
пока неизвестны. Все вершины графа помечаются как непосещённые.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В
противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая
минимальную
метку.
Мы
рассматриваем
всевозможные
маршруты,
в
которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u,
назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных
как посещённые, рассмотрим новую длину пути, равную сумме значений текущей
метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение
длины меньше значения метки соседа, заменим значение метки полученным
значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и
повторим шаг алгоритма.

8.

Кратчайший путь: алгоритм Дейкстры
Пример
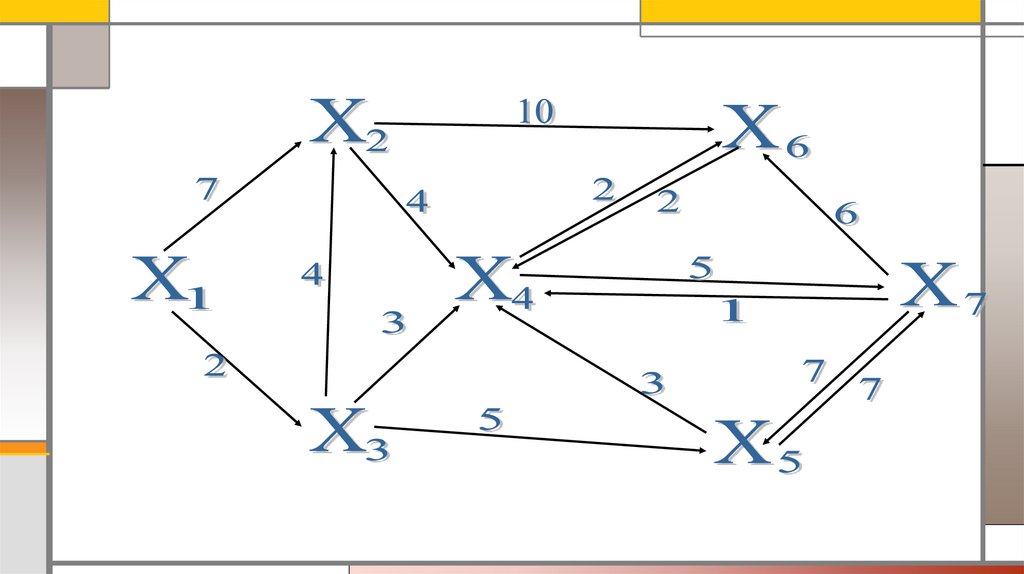
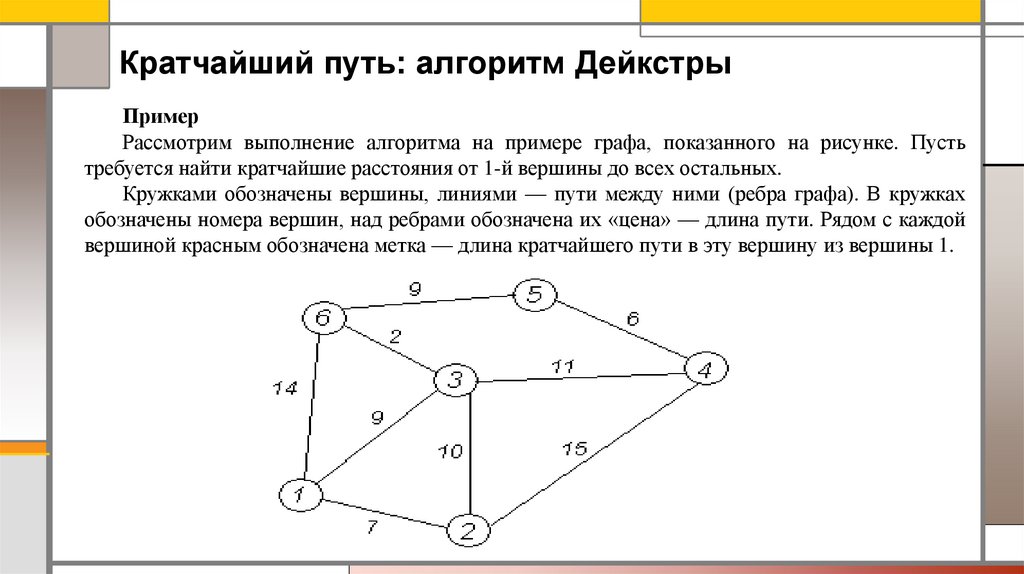
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть
требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках
обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой
вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.

9.

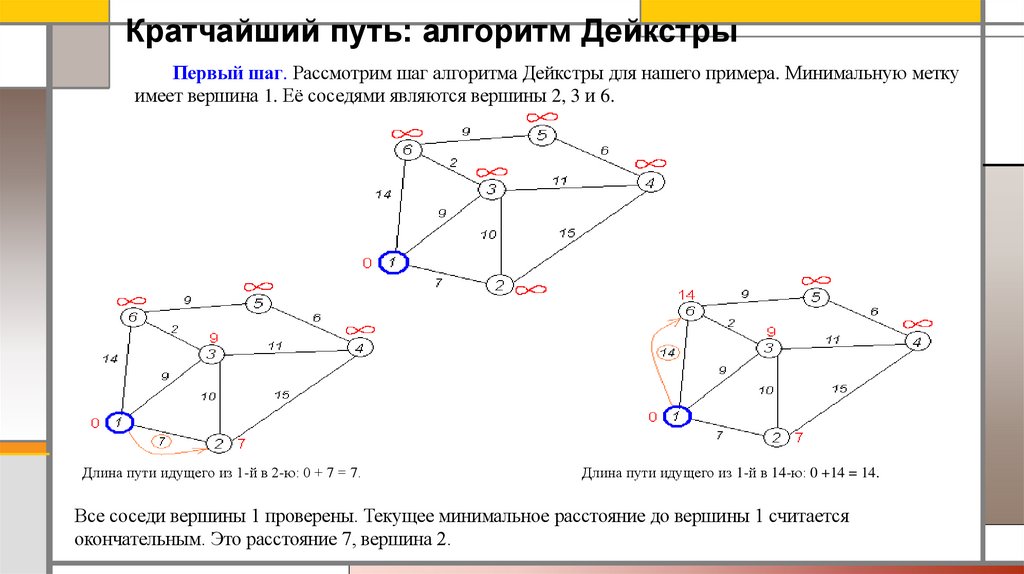
Кратчайший путь: алгоритм Дейкстры
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку
имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
Длина пути идущего из 1-й в 2-ю: 0 + 7 = 7.
Длина пути идущего из 1-й в 14-ю: 0 +14 = 14.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается
окончательным. Это расстояние 7, вершина 2.

10.

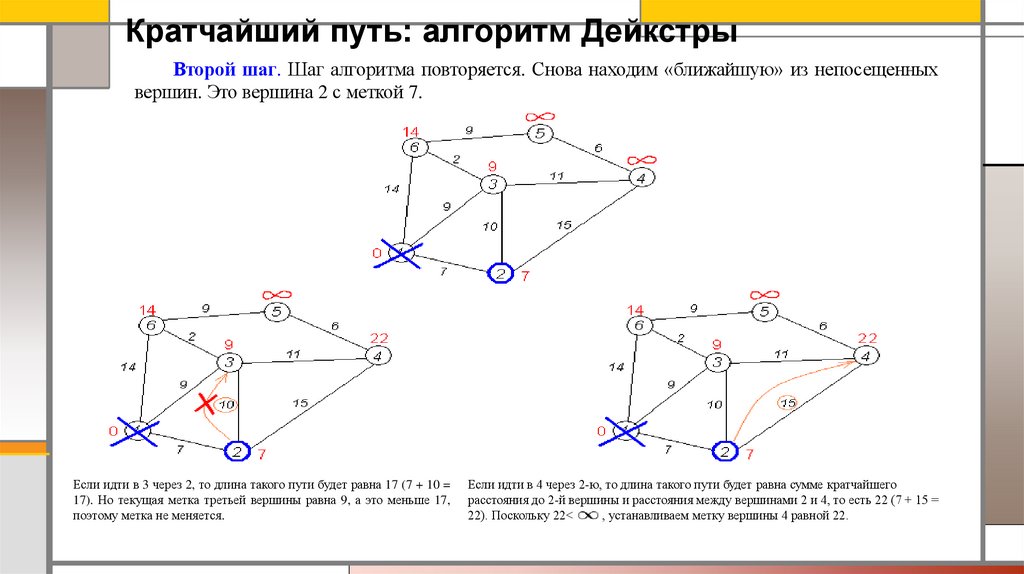
Кратчайший путь: алгоритм Дейкстры
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных
вершин. Это вершина 2 с меткой 7.
Если идти в 3 через 2, то длина такого пути будет равна 17 (7 + 10 =
17). Но текущая метка третьей вершины равна 9, а это меньше 17,
поэтому метка не меняется.
Если идти в 4 через 2-ю, то длина такого пути будет равна сумме кратчайшего
расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 =
22). Поскольку 22<
, устанавливаем метку вершины 4 равной 22.

11.

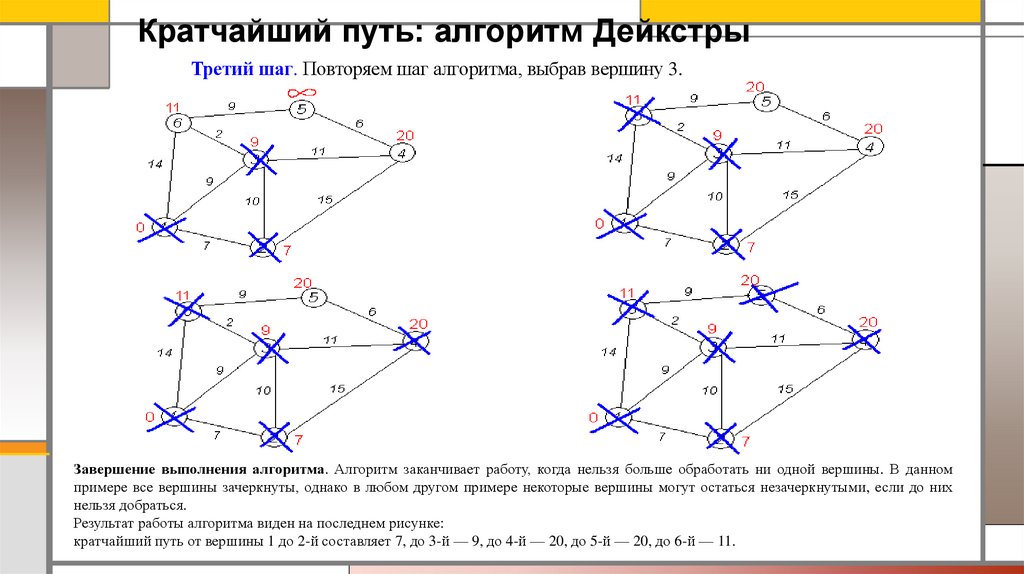
Кратчайший путь: алгоритм Дейкстры
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном
примере все вершины зачеркнуты, однако в любом другом примере некоторые вершины могут остаться незачеркнутыми, если до них
нельзя добраться.
Результат работы алгоритма виден на последнем рисунке:
кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.

12.

Кратчайший путь: алгоритм Дейкстры
1. Начальные присваивания.
Каждой вершине, кроме начальной, сопоставим вес l(ai)= ,
назовем этот вес временным.
Начальной вершине сопоставим вес l(aн)=0,
этот вес назовем постоянным,
вершину aн назовем текущей и обозначим как p.
2. Обновление весов.
Всем вершинам, связанным с текущей по исходящим дугам и имеющим
временные веса, изменим веса по правилу
l(аi)=min(l(аi), l(p)+сp,i)
3. Смена текущей вершины.
Среди вершин с временной оценкой найдем вершину с минимальным
весом.
Назовем ее текущей и обозначим как p,
а ее вес назовем постоянным.
Если это есть вершина aк, то перейдем к пункту 4, иначе – к пункту 2.

13.

Кратчайший путь: алгоритм Дейкстры
4. Выделение пути обратным ходом.
Определим конечную вершину как текущую.
1 способ:
в столбце p таблицы решения находим строку, в которой
текущая вершина впервые получила свой постоянный вес;
вершину, записанную в столбце p таблицы, назовем
текущей, и отнесем ее к пути.
2 способ:
для каждой вершины, связанной с ней по заходящим дугам,
определим разность между весом текущей вершины и
весом дуги;
вершину, вес которой совпадает с этой разностью, назовем
текущей, а дугу отнесем к пути.
повторим эту процедуру до тех пор, пока текущей не станет
начальная вершина.

14.

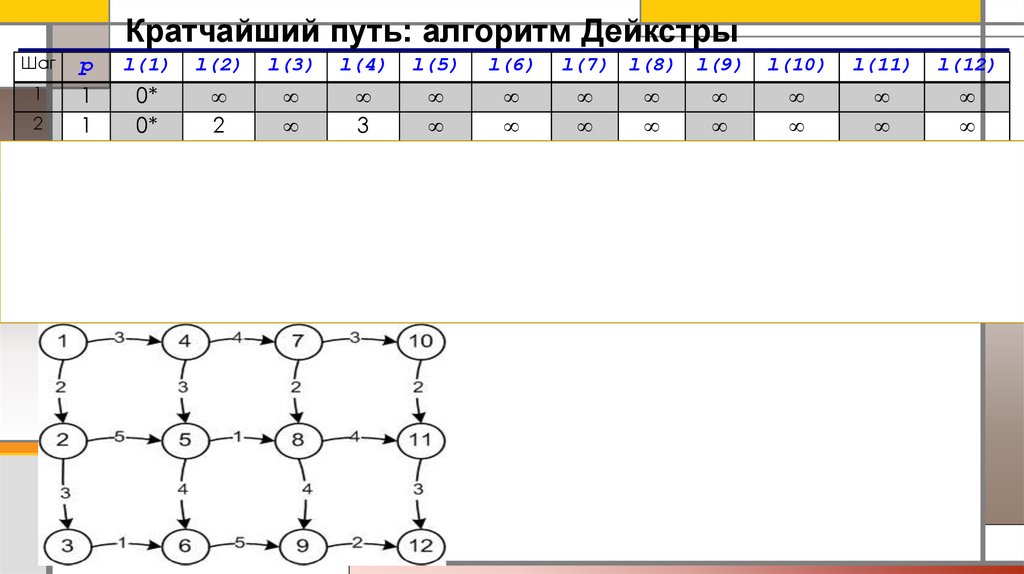
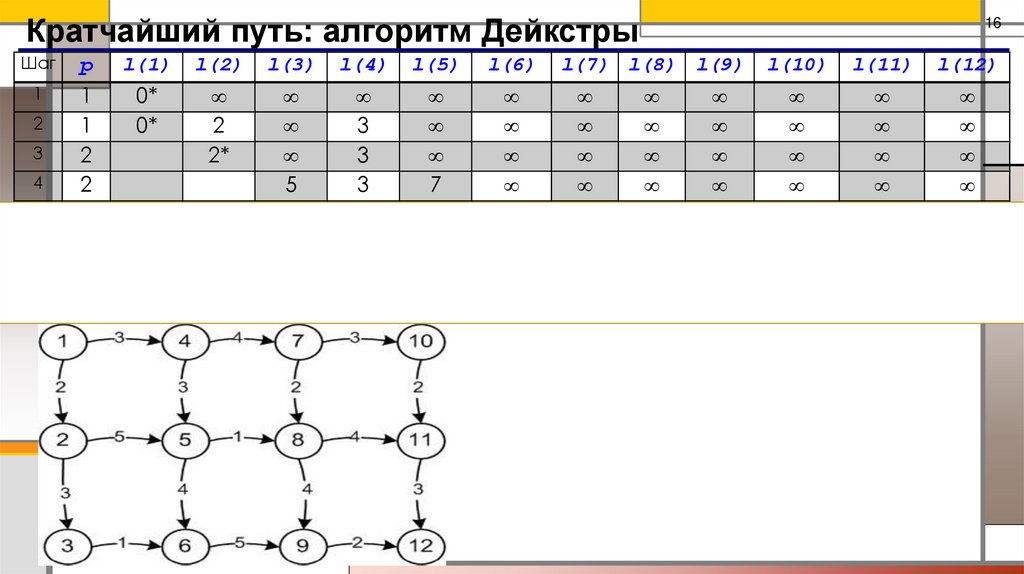
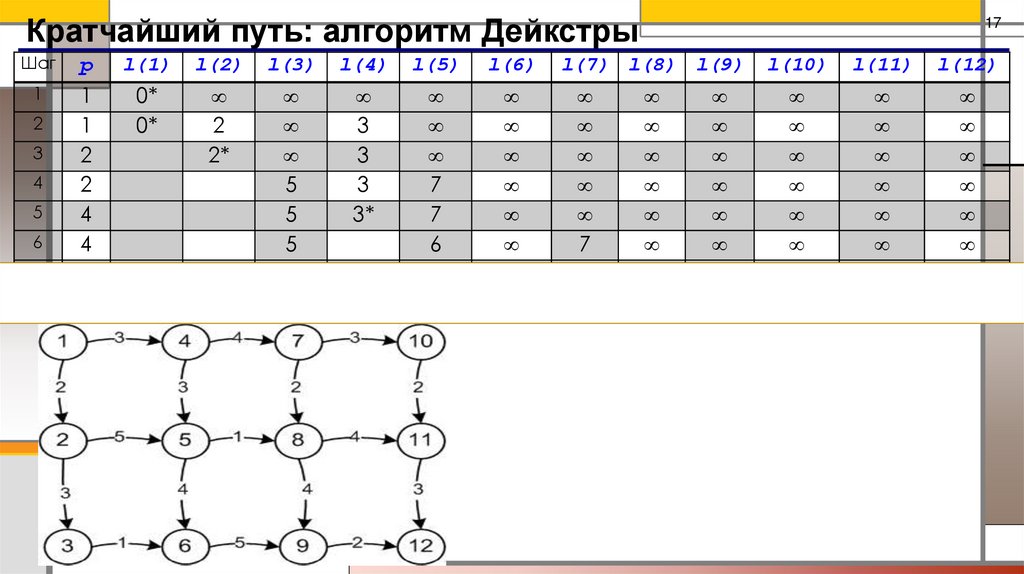
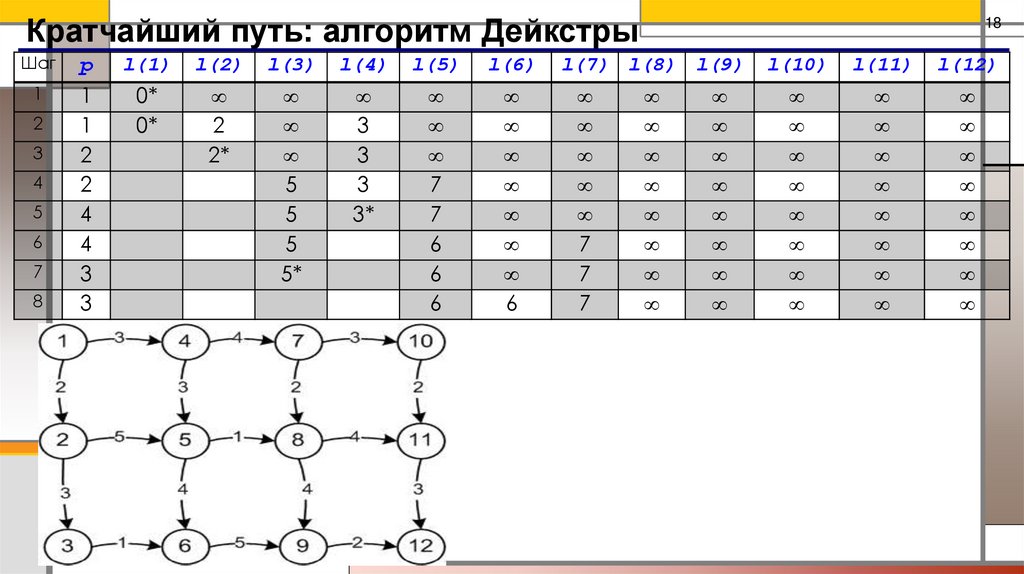
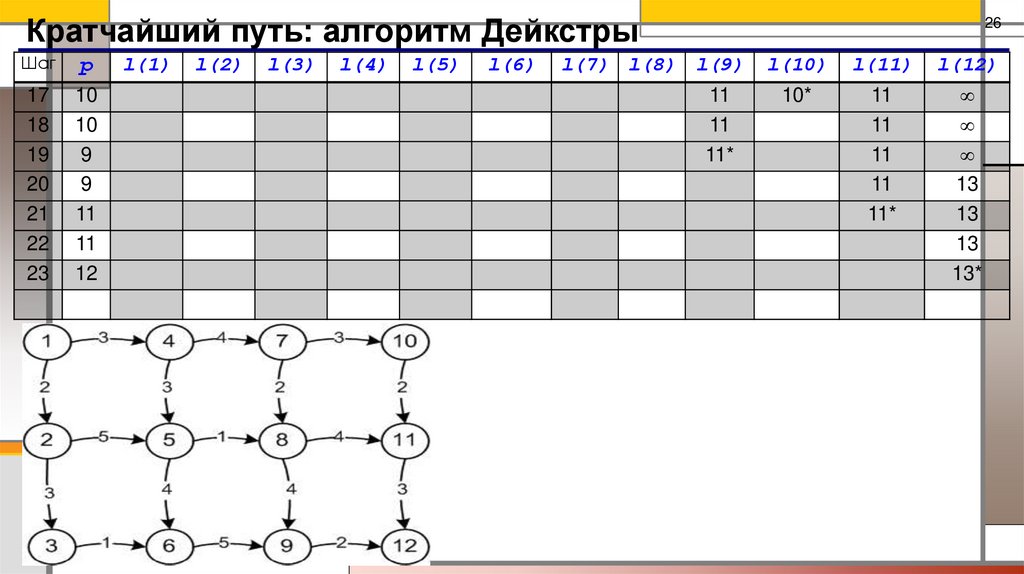
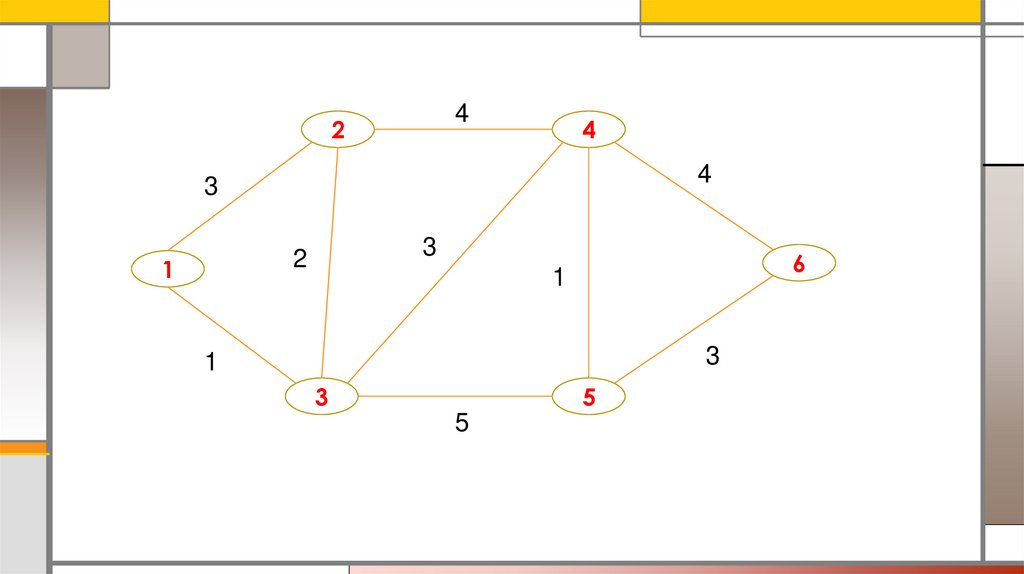
Кратчайший путь: алгоритм Дейкстры
Пример. Задан граф. Найти кратчайший путь между вершиной 1 и 12.

15.

Кратчайший путь: алгоритм Дейкстры
Шаг
1
2
3
2
3
2
3
2
p
1
1
2
2
4
4
3
3
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
0*
0*
2
2*
5
5
5
5*
3
3
3
3*
7
7
6
6
6
6
l(7) l(8) l(9)
7
7
7
l(10)
l(11)
l(12)

16.

Кратчайший путь: алгоритм Дейкстры
Шаг
1
2
3
4
3
2
3
2
p
1
1
2
2
4
4
3
3
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
0*
0*
2
2*
5
5
5
5*
3
3
3
3*
7
7
6
6
6
6
16
l(7) l(8) l(9)
7
7
7
l(10)
l(11)
l(12)

17.

Кратчайший путь: алгоритм Дейкстры
Шаг
1
2
3
4
5
6
3
2
p
1
1
2
2
4
4
3
3
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
0*
0*
2
2*
5
5
5
5*
3
3
3
3*
7
7
6
6
6
6
17
l(7) l(8) l(9)
7
7
7
l(10)
l(11)
l(12)

18.

Кратчайший путь: алгоритм Дейкстры
Шаг
1
2
3
4
5
6
7
8
p
1
1
2
2
4
4
3
3
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
0*
0*
2
2*
5
5
5
5*
3
3
3
3*
7
7
6
6
6
6
18
l(7) l(8) l(9)
7
7
7
l(10)
l(11)
l(12)

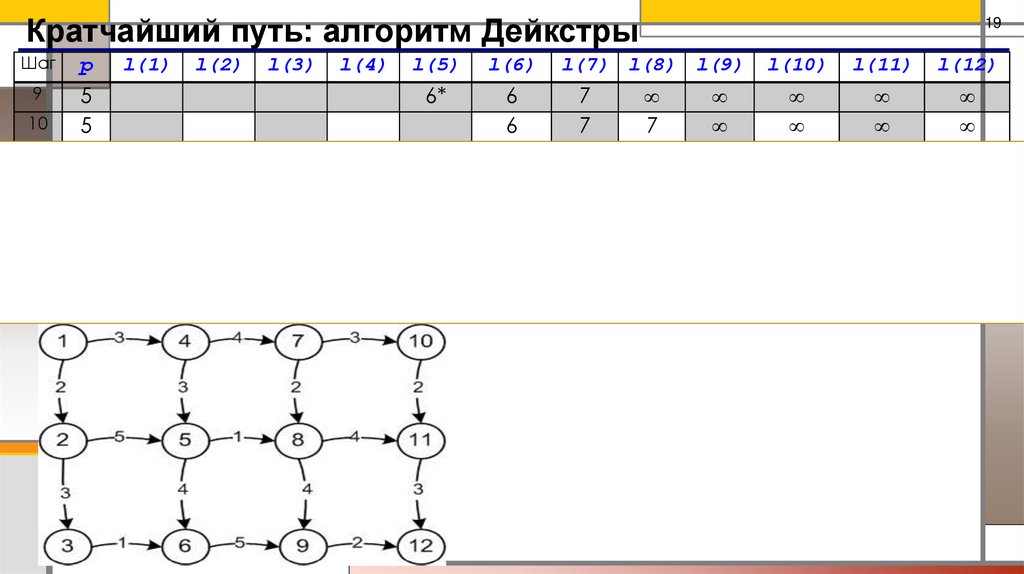
19.

Кратчайший путь: алгоритм Дейкстры
Шаг
3
p
5
5
6
2
3
2
3
2
6
7
7
8
8
9
10
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
6*
6
6
6*
19
l(7) l(8) l(9)
l(10)
l(11)
l(12)
7
7
7
7
7
7
7*
7
7
7
7*
11
11
11
11
11
10
10
10
11

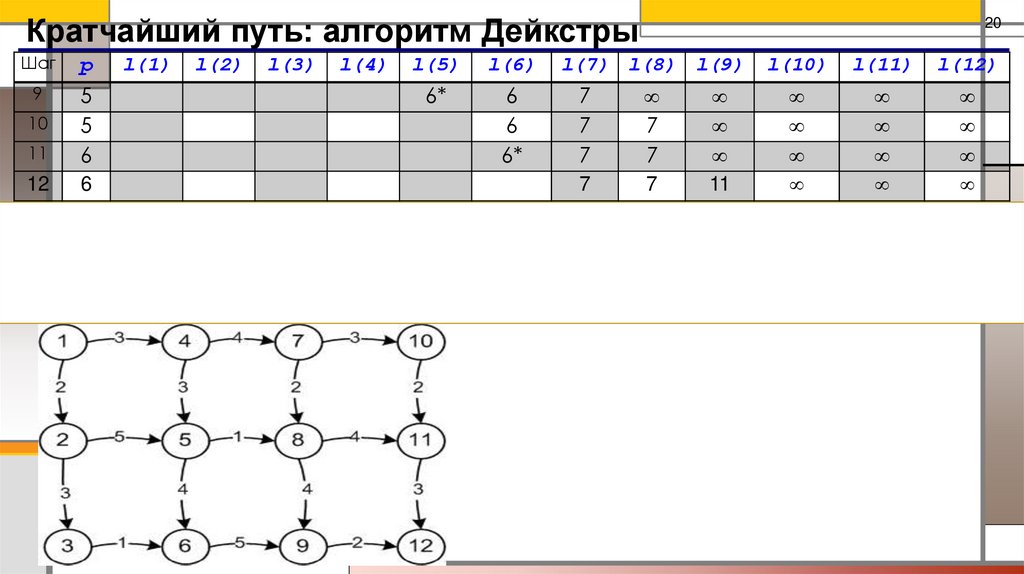
20.

Кратчайший путь: алгоритм Дейкстры
Шаг
11
p
5
5
6
12
3
2
3
2
6
7
7
8
8
9
10
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
6*
6
6
6*
20
l(7) l(8) l(9)
l(10)
l(11)
l(12)
7
7
7
7
7
7
7*
7
7
7
7*
11
11
11
11
11
10
10
10
11

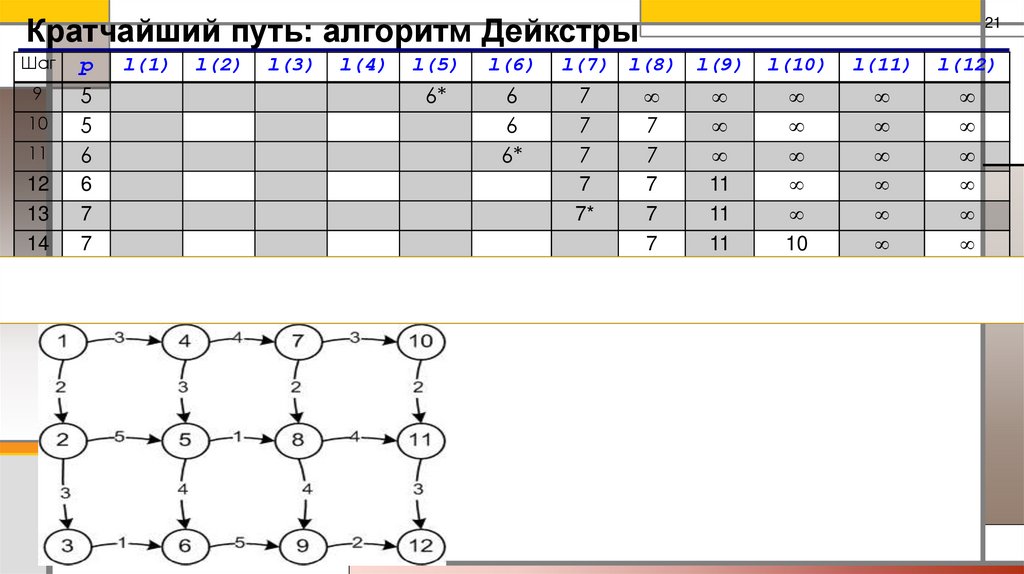
21.

Кратчайший путь: алгоритм Дейкстры
Шаг
11
p
5
5
6
12
13
14
3
2
6
7
7
8
8
9
10
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
6*
6
6
6*
21
l(7) l(8) l(9)
l(10)
l(11)
l(12)
7
7
7
7
7
7
7*
7
7
7
7*
11
11
11
11
11
10
10
10
11

22.

Кратчайший путь: алгоритм Дейкстры
Шаг
11
p
5
5
6
12
13
14
15
16
6
7
7
8
8
9
10
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
6*
6
6
6*
22
l(7) l(8) l(9)
l(10)
l(11)
l(12)
7
7
7
7
7
7
7*
7
7
7
7*
11
11
11
11
11
10
10
10
11

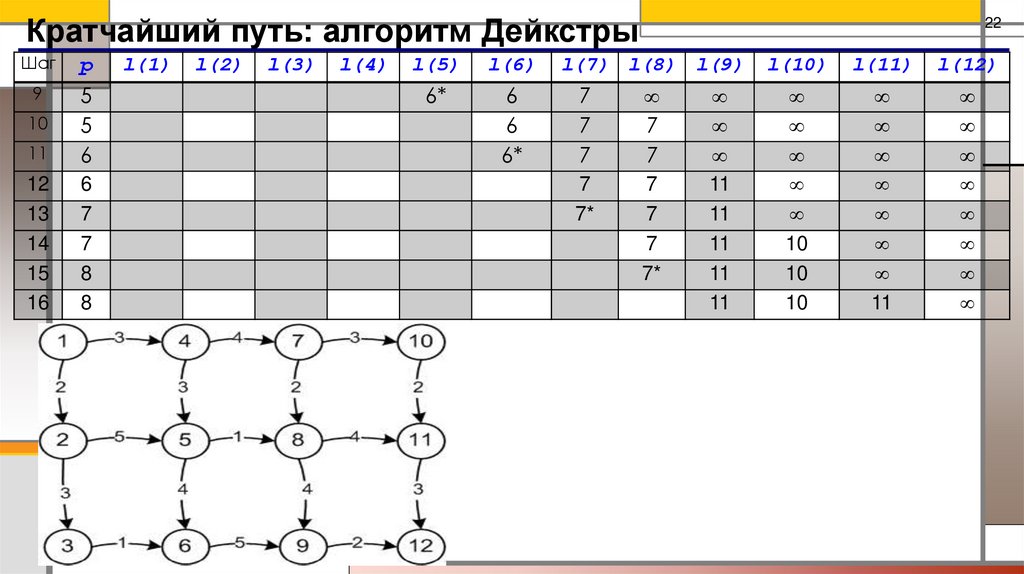
23.

Кратчайший путь: алгоритм Дейкстры
Шаг
p
17
18
3
2
3
2
3
4
10
10
9
9
11
11
12
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
23
l(7) l(8) l(9)
11
11
11*
l(10)
l(11)
l(12)
10*
11
11
11
11
11*
13
13
13
13*

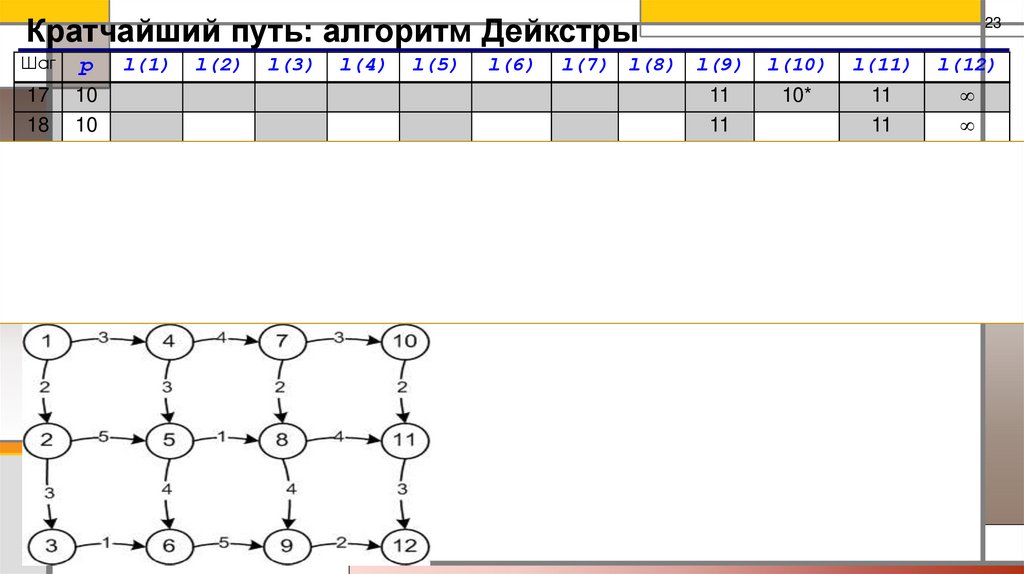
24.

Кратчайший путь: алгоритм Дейкстры
Шаг
p
17
18
19
20
3
2
3
4
10
10
9
9
11
11
12
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
24
l(7) l(8) l(9)
11
11
11*
l(10)
l(11)
l(12)
10*
11
11
11
11
11*
13
13
13
13*

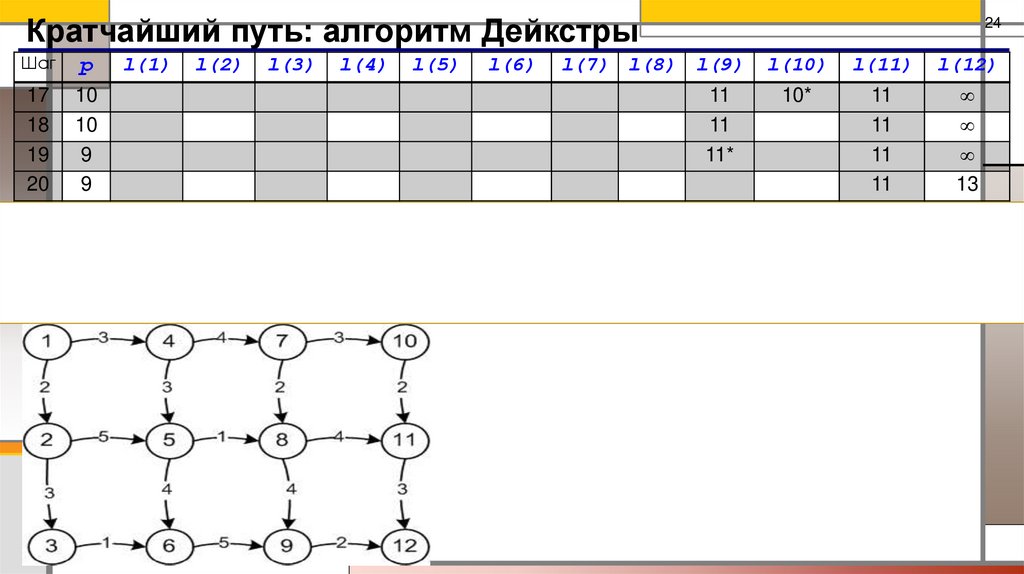
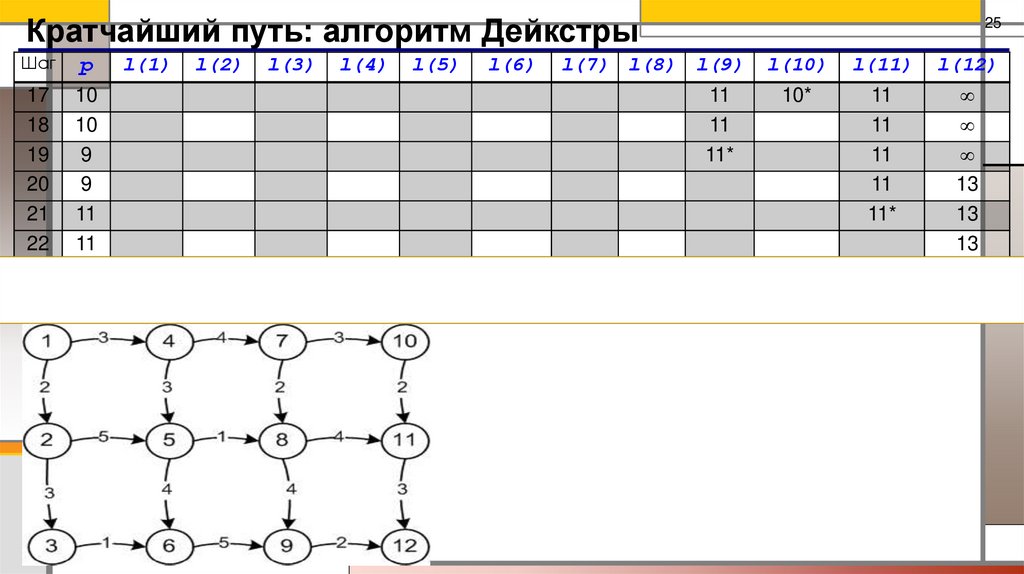
25.

Кратчайший путь: алгоритм Дейкстры
Шаг
p
17
18
19
20
21
22
3
4
10
10
9
9
11
11
12
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
25
l(7) l(8) l(9)
11
11
11*
l(10)
l(11)
l(12)
10*
11
11
11
11
11*
13
13
13
13*

26.

Кратчайший путь: алгоритм Дейкстры
Шаг
p
17
18
19
20
21
22
23
10
10
9
9
11
11
12
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
26
l(7) l(8) l(9)
11
11
11*
l(10)
l(11)
l(12)
10*
11
11
11
11
11*
13
13
13
13*

27.

Кратчайший путь: алгоритм Дейкстры
Шаг
p
17
18
19
20
21
22
23
10
10
9
9
11
11
12
l(1)
l(2)
l(3)
l(4)
l(5)
l(6)
27
l(7) l(8) l(9)
11
11
11*
l(10)
l(11)
l(12)
10*
11
11
11
11
11*
13
13
13
13*
Выполняя шаг 4 алгоритма, выделим путь
12 – 9 – 6 – 3 – 2 – 1.
Но существует еще один путь той же длины –
12 – 9 – 8 – 5 – 4 – 1,
т.к. для вершины 9 имеем два одинаковых по длине
пути к началу, проходящих через вершины 8 и 6.

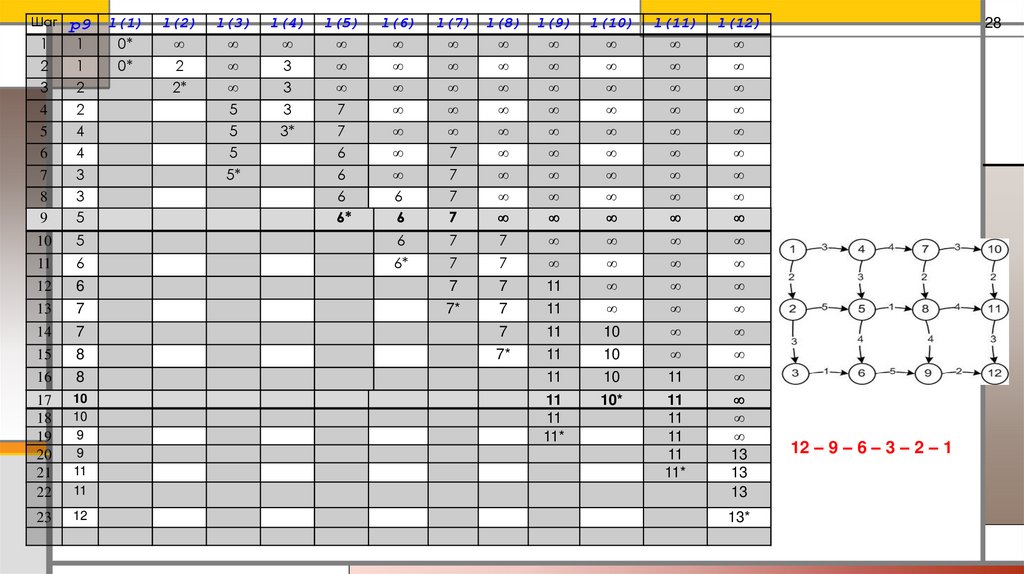
28.

Шаг
p9 l(1)
0*
0*
l(2)
2
2*
l(3)
5
5
5
5*
l(4)
3
3
3
3*
l(5)
7
7
6
6
6
6*
l(6)
6
6
l(7) l(8) l(9)
7
7
7
7
l(10)
l(11)
l(12)
1
2
3
4
5
6
7
8
9
1
1
2
2
4
4
3
3
5
10
5
6
7
7
11
6
6*
7
7
12
6
7
7
11
13
7
7*
7
11
14
7
7
11
10
15
8
7*
11
10
16
8
11
10
11
17
18
19
20
21
22
10
10
9
9
11
11
11
11
11*
10*
11
11
11
11
11*
13
13
13
23
12
13*
28
12 – 9 – 6 – 3 – 2 – 1

29.

4
2
4
4
3
3
2
1
6
1
3
1
3
5
5

30.

31.

Кратчайшие пути между парами вершин
Предположим, что
мы имеем взвешенный орграф, который содержит время полета по
маршрутам, связывающим определенные города,
и мы хотим построить таблицу, где приводилось бы минимальное
время перелета из одного (произвольного) города в любой другой.
В этом случае мы сталкиваемся с общей задачей нахождения
кратчайших путей,
т.е. нахождения кратчайших путей между всеми парами
вершин орграфа.

32.

Кратчайшие пути между парами вершин
Формулировка задачи
Есть ориентированный граф G=(V, U), каждой дуге (ребру) (i, j)
этого графа сопоставлен неотрицательный вес cij.
Общая задача нахождения кратчайших путей заключается в
нахождении для каждой упорядоченной пары вершин i, j любого
пути от вершины i в вершину j, длина которого минимальна
среди всех возможных путей от i к j.
Можно решать эту задачу, последовательно применяя алгоритм
Дейкстры для каждой вершины, объявляемой в качестве источника.
Но мы для решения поставленной задачи воспользуемся алгоритмом,
предложенным Флойдом (R.W.Floyd).

33.

Кратчайшие пути между парами вершин
Алгоритм Флойда
Пусть все вершины орграфа последовательно пронумерованы
от 1 до n.
Алгоритм Флойда использует матрицу An n, в которой находятся
длины кратчайших путей:
Aij = cij, если i j;
Aij = 0, если i=j;
Aij = , если отсутствует путь из вершины i в вершину j.

34.

Кратчайшие пути между парами вершин
34
Над матрицей A выполняется n итераций.
После k-й итерации Aij содержит значение наименьшей длины пути из
вершины i в вершину j,
причем путь не проходит через вершины с номерами большими k.
Вычисление на k-ой итерации выполняется по формуле:
Aij min
k
A , A A
k 1
k 1
k 1
ij
ik
kj
Верхний индекс k обозначает значение матрицы A после k-ой итерации.
k 1
k
Для вычисления Aij проводится сравнение величины Aij
• (т.е. стоимость пути от вершины i к вершине j без участия вершины k или другой
вершины с более высоким номером)
k 1
с величиной A
ik
k 1
Akj
• (т.е. стоимость пути от вершины i к вершине k плюс стоимость пути от вершины k до
вершины j).
k 1
k
Если путь через вершину k дешевле, чем Aij , то величина Aij изменяется.

35.

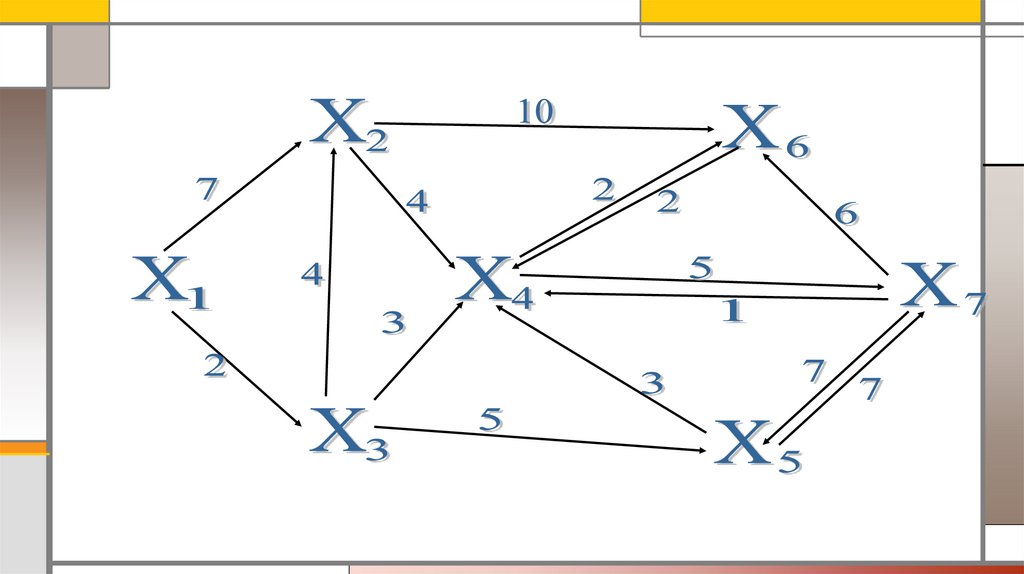
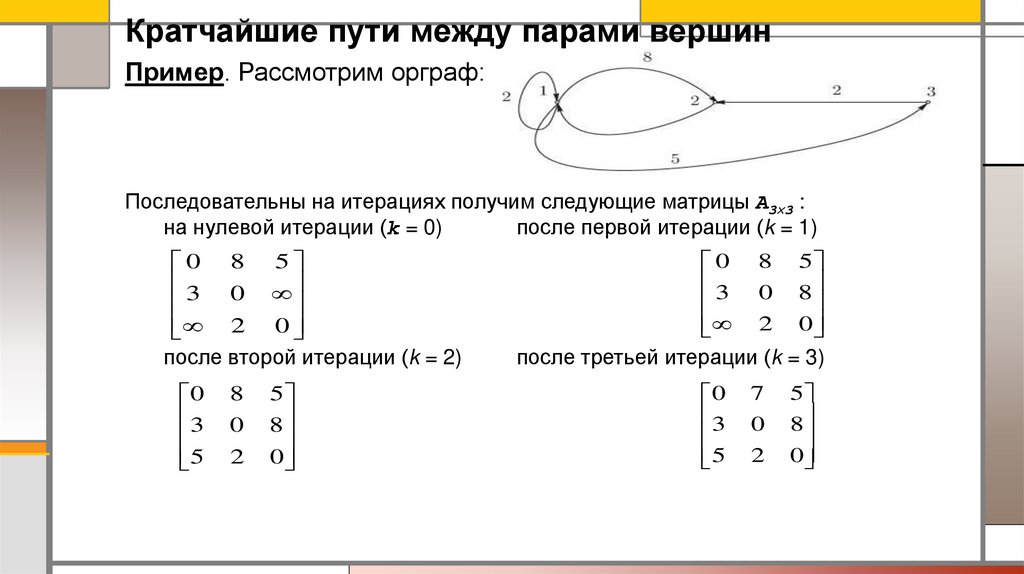
Кратчайшие пути между парами вершин
Пример. Рассмотрим орграф:
Последовательны на итерациях получим следующие матрицы A3 3 :
на нулевой итерации (k = 0)
после первой итерации (k = 1)
0 8 5
3 0
2 0
после второй итерации (k = 2)
0
3
5
8
0
2
5
8
0
0 8 5
3 0 8
2 0
после третьей итерации (k = 3)
0
3
5
7
0
2
5
8
0