Similar presentations:
Ориентированные графы. Нахождение кратчайших путей в орграфе. Алгоритм Дейкстры
1.
2.
Маршруты, цепи, циклыМаршрутом в графе называется чередующаяся последовательность
вершин и ребер, в которой любые два соседних элемента инцидентны:
v0 , e1 , v1 , e2 , v 2 ,..., ek , vk
Если v0 vk , то маршрут замкнут, в противном случае открыт.
Если все ребра различны, то маршрут называется цепью.
Если все вершины различны, то маршрут называется простой цепью. В
цепи v0 , e1 , v1 , e2 , v2 ,..., ek , vk вершины v0 и vk называются концами цепи,
т. е. цепь концами v0 и vk соединяет вершины v0 и vk. Цепь, соединяющая
вершины v0 и vk , обозначается (v0 и vk ).
Замкнутая цепь называется циклом, замкнутая простая – простым
циклом, число циклов обозначается z(G). Граф без циклов – ациклический.
Длинной маршрута называется количество ребер в нем (с повторениями).
Если маршрут M v0 , e1 , v1 , e2 , v2 ,..., ek , vk , то длина маршрута М равна k,
обозначается M k.
3.
Ориентированные графыЕсли элементы множества Е графа G(V, E) – упорядоченные пары, то
граф называется ориентированным или орграфом.
Ребро графа называется ориентированным, если одну вершину ребра
считают началом ребра а другую концом, на рисунке изображают стрелкой
между вершинами. Граф у которого все ребра ориентированы –
ориентированный.
Ориентированное ребро
Рис 1
Неориентированное ребро
Рис 2
Одна и та же вершина ориентированного графа может служить началом
для одних ребер и концом для других, поэтому различают две степени
вершины:
• Степенью выхода вершины орграфа – число выходящих из вершины
ребер;
• Степенью входа вершины орграфа – число входящих в вершину ребер.
4.
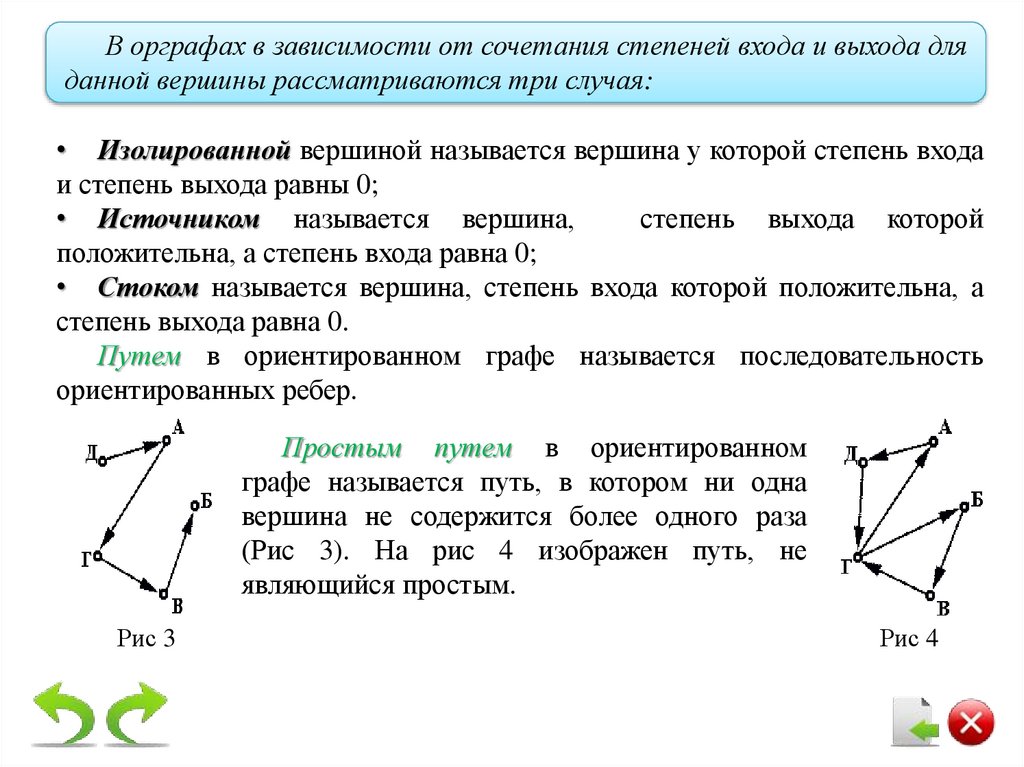
В орграфах в зависимости от сочетания степеней входа и выхода дляданной вершины рассматриваются три случая:
• Изолированной вершиной называется вершина у которой степень входа
и степень выхода равны 0;
• Источником называется вершина,
степень выхода которой
положительна, а степень входа равна 0;
• Стоком называется вершина, степень входа которой положительна, а
степень выхода равна 0.
Путем в ориентированном графе называется последовательность
ориентированных ребер.
Простым путем в ориентированном
графе называется путь, в котором ни одна
вершина не содержится более одного раза
(Рис 3). На рис 4 изображен путь, не
являющийся простым.
Рис 3
Рис 4
5.
Замкнутыйпуть
в
ориентированном
графе
называется
ориентированным циклом или контуром. Длиной пути называется число
ребер в этом пути.
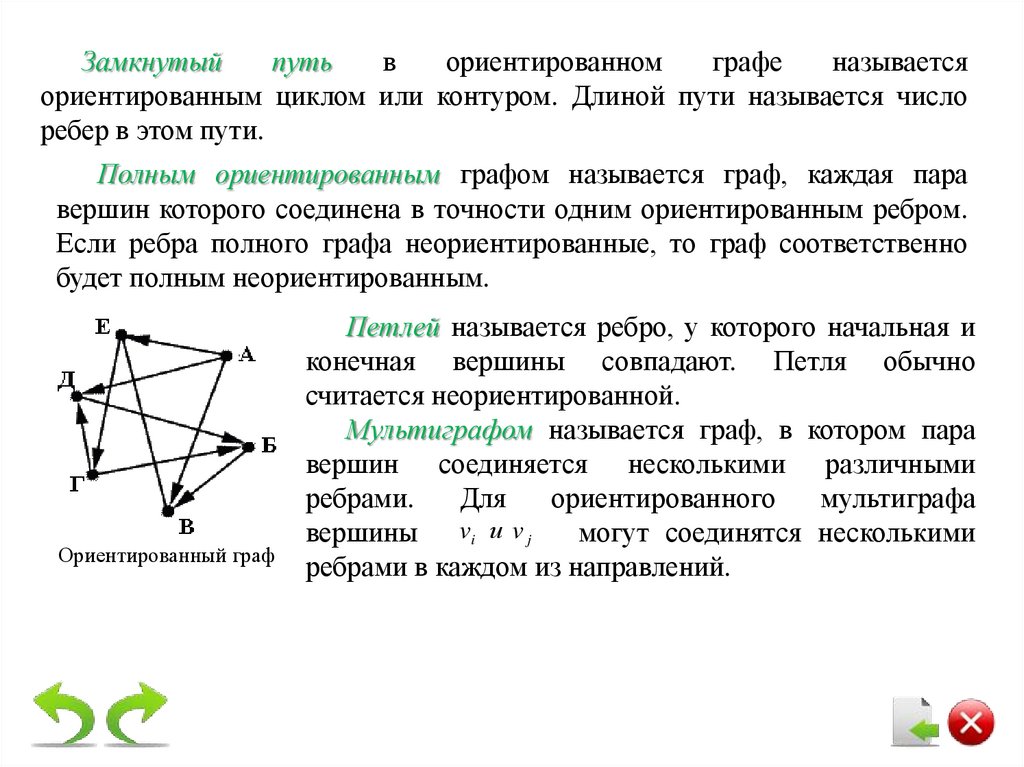
Полным ориентированным графом называется граф, каждая пара
вершин которого соединена в точности одним ориентированным ребром.
Если ребра полного графа неориентированные, то граф соответственно
будет полным неориентированным.
Ориентированный граф
Петлей называется ребро, у которого начальная и
конечная вершины совпадают. Петля обычно
считается неориентированной.
Мультиграфом называется граф, в котором пара
вершин соединяется несколькими различными
ребрами.
Для
ориентированного
мультиграфа
вершины vi и v j
могут соединятся несколькими
ребрами в каждом из направлений.
6.
КратчайшиеКратчайшие пути
пути вв орграфе
орграфе
Пусть G=(V, А) – взвешенный орграф, т.е. каждой его дуге e=(u,v)
поставлено в соответствие неотрицательное число (e) (u, v)
,
называемое весом. Расстоянием между произвольными вершинами s и t
орграфа назовем наименьший вес пути из s в t
d ( s, t ) min ( P),
P: s ... t
где ( P) (e) вес пути P
Вес тривиального пути равен 0. Если пути между вершинами не
существует, то полагаем, что путь равен
7.
ЗАДАЧА О КРАТЧАЙШЕМ ПУТИЗадача о кратчайшем пути— задача поиска самого короткого
пути (цепи) между двумя точками (вершинами) на графе, в
которой минимизируется сумма весов рёбер, составляющих
путь.
в GPS-навигаторах осуществляется поиск кратчайшего пути
между двумя перекрестками. В качестве вершин выступают
перекрестки, а дороги являются ребрами, которые лежат между
ними. Если сумма длин дорог между перекрестками
минимальна, тогда найденный путь самый короткий.
8.
ВАРИАНТЫ ПОСТАНОВКИ ЗАДАЧИЗадача о кратчайшем пути в заданный пункт назначения.
Требуется найти кратчайший путь в заданную вершину
назначения t, который начинается в каждой из вершин графа
(кроме t).
Задача о кратчайшем пути между заданной парой вершин.
Требуется найти кратчайший путь из заданной вершины u в
заданную вершину v.
Задача о кратчайшем пути между всеми парами вершин.
Требуется найти кратчайший путь из каждой вершины u в каждую
вершину v.
9.
НАИБОЛЕЕ ПОПУЛЯРНЫЕАЛГОРИТМЫ
Алгоритм Дейкстры находит кратчайший путь от одной из
вершин графа до всех остальных
Алгоритм Беллмана — Форда находит кратчайшие пути от одной
вершины графа до всех остальных во взвешенном графе. Вес
ребер может быть отрицательным
Алгоритм поиска A* находит маршрут с наименьшей стоимостью
от одной вершины (начальной) к другой (целевой, конечной),
используя алгоритм поиска по первому наилучшему совпадению
на графе
Алгоритм Флойда — Уоршелла находит кратчайшие пути между
всеми вершинами взвешенного ориентированного графа
10.
АЛГОРИТМ ДЕЙКСТРЫЗадан орграф G(V,A), каждой дуге (u,v) ставится в соответствие
число L(u,v) – длина дуги (расстояния, стоимости и т.п.)
В общем случае возможно L > 0, L < 0, L = 0.
Под длиной пути понимаем, как и прежде, сумму длин дуг,
составляющих путь.
Найти длины кратчайших путей и сами пути от вершины s до всех
остальных вершин графа vi.
Известна схема дорог. Требуется перевезти груз из одного пункта в
другой по маршруту минимальной длины.
Если в графе нет циклов с отрицательной длиной, то кратчайшие
пути существуют и любой кратчайший путь – это простая цепь.
11.
Эдсгер Дейкстра (Edsger Wybe Dijkstra) –нидерландский ученый (структурное
программирование, язык Алгол,
семафоры, распределенные вычисления)
Лауреат премии Тьюринга (ACM A.M.
Turing Award)
1. Дейкстра Э. Дисциплина
программирования = A discipline of
programming.
2. Дал У., Дейкстра Э., Хоор К. Структурное
программирование = Structured
Programming.
Алгоритм основан на приписывании вершинам vi временных
меток d(vi). Метка вершины дает верхнюю границу длины пути от
s к этой вершине
12.
Шаг 1 (начальная установка).Процесс построения дерева начинается с заданной вершины.
Положить d(s)=0, считать метку постоянной.
d(vi)=∞, i=1...n, считать метки временными. p=s.
Шаг 2 (общий шаг).
В дальнейшем на каждом шаге к дереву присоединяется одно
новое ребро (и одна вершина). Это ребро выбирается из
подходящих ребер, причем подходящим считается ребро,
соединяющее вершину дерева с вершиной, ему не
принадлежащей. Среди подходящих ребер выбирается ребро
наименьшего веса.
Повторяется n раз, пока не будут упорядочены все вершины.
13.
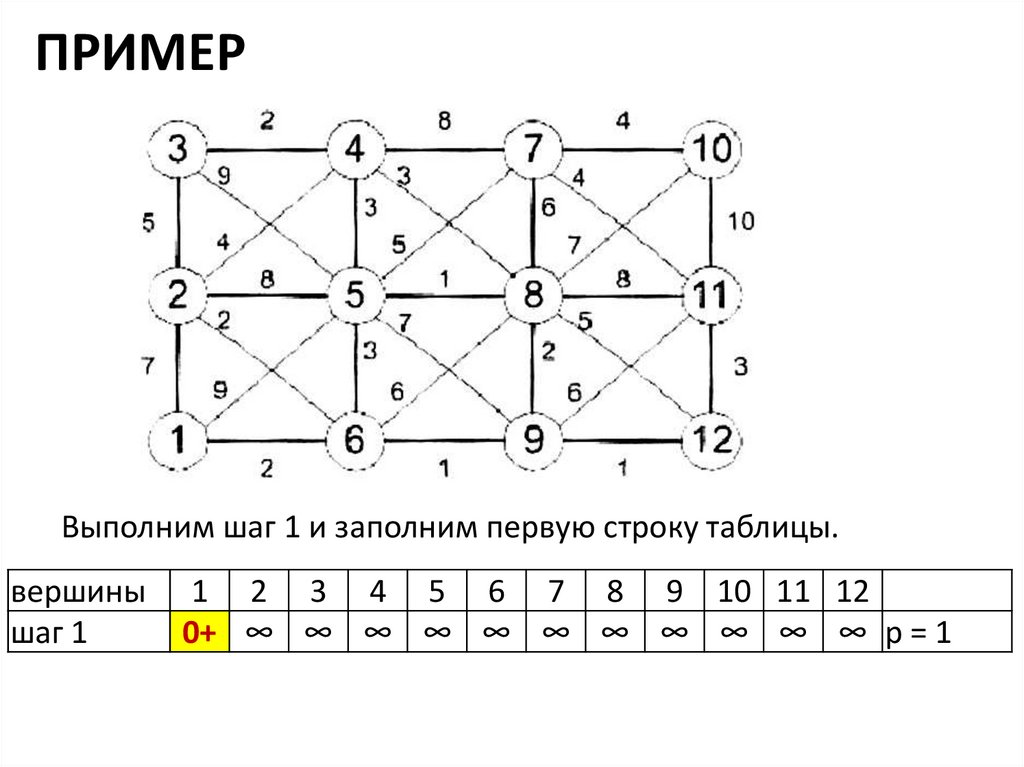
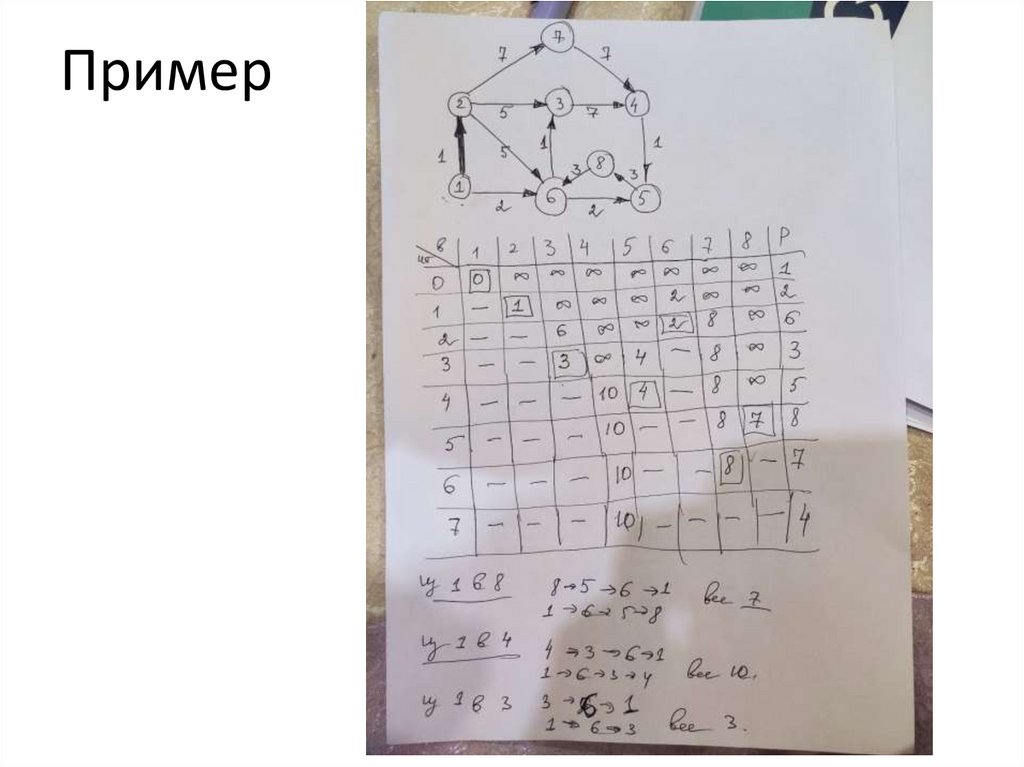
ПРИМЕРВыполним шаг 1 и заполним первую строку таблицы.
вершины
шаг 1
1 2 3 4 5 6 7 8 9 10 11 12
0+ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ p = 1
14.
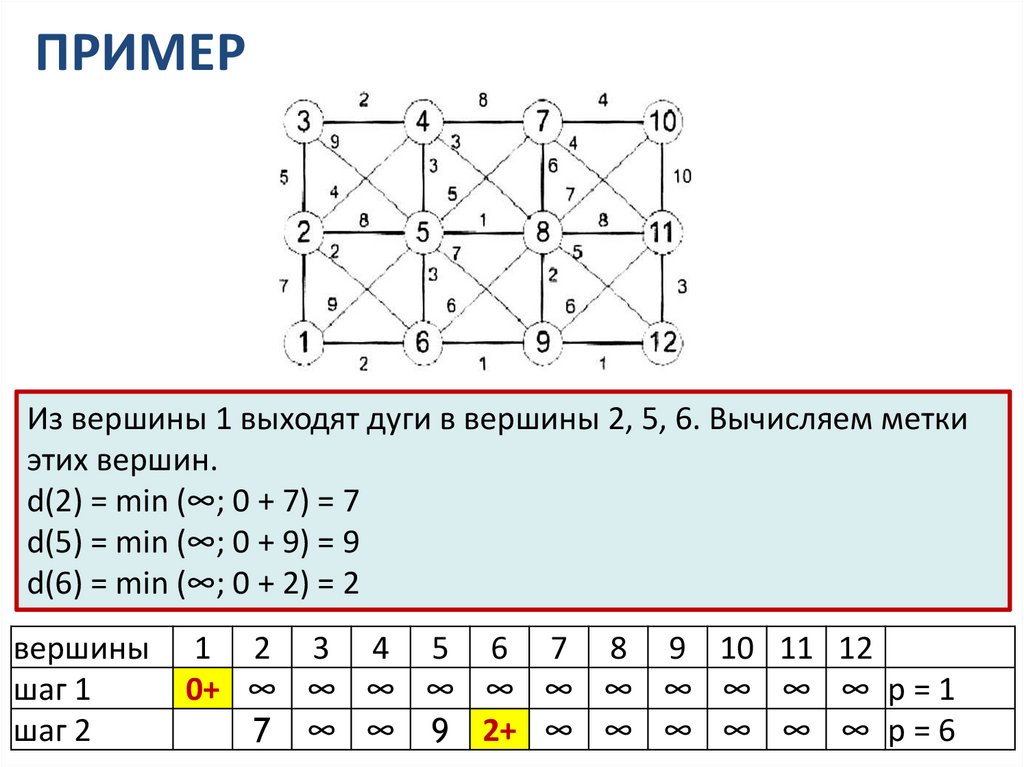
ПРИМЕРИз вершины 1 выходят дуги в вершины 2, 5, 6. Вычисляем метки
этих вершин.
d(2) = min (∞; 0 + 7) = 7
d(5) = min (∞; 0 + 9) = 9
d(6) = min (∞; 0 + 2) = 2
вершины
шаг 1
шаг 2
1 2 3 4 5 6 7 8 9 10 11 12
0+ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ p = 1
7 ∞ ∞ 9 2+ ∞ ∞ ∞ ∞ ∞ ∞ p = 6
15.
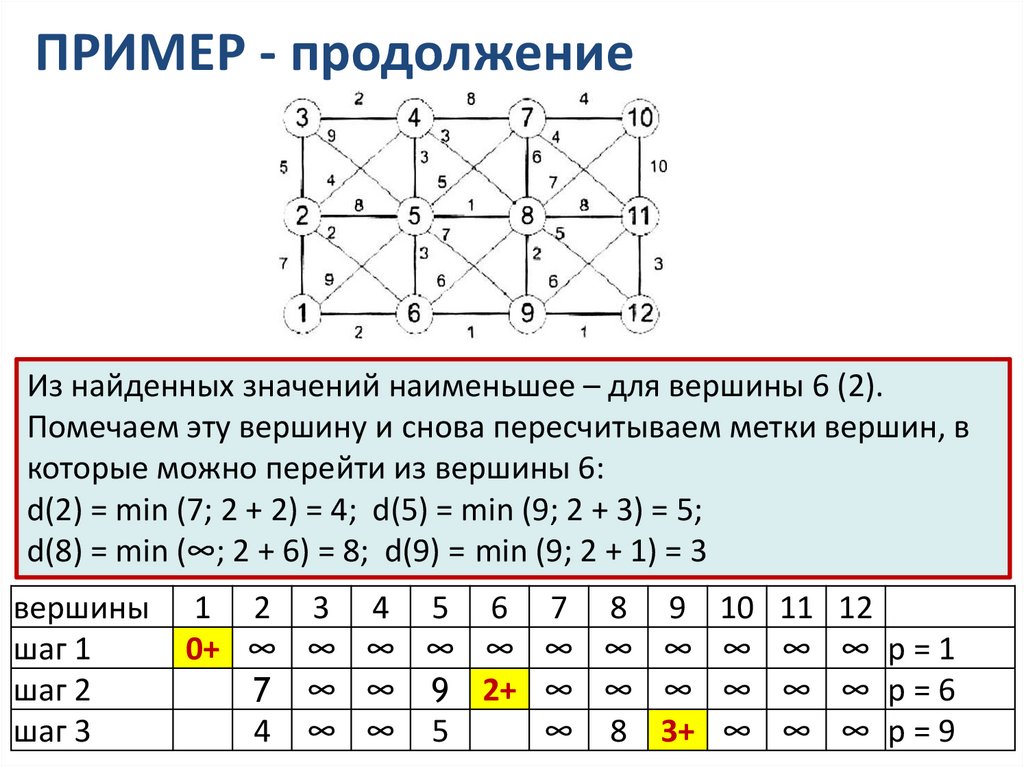
ПРИМЕР - продолжениеИз найденных значений наименьшее – для вершины 6 (2).
Помечаем эту вершину и снова пересчитываем метки вершин, в
которые можно перейти из вершины 6:
d(2) = min (7; 2 + 2) = 4; d(5) = min (9; 2 + 3) = 5;
d(8) = min (∞; 2 + 6) = 8; d(9) = min (9; 2 + 1) = 3
вершины
шаг 1
шаг 2
шаг 3
1 2 3 4 5 6 7 8 9 10
0+ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
7 ∞ ∞ 9 2+ ∞ ∞ ∞ ∞
4 ∞ ∞ 5
∞ 8 3+ ∞
11
∞
∞
∞
12
∞ p=1
∞ p=6
∞ p=9
16.
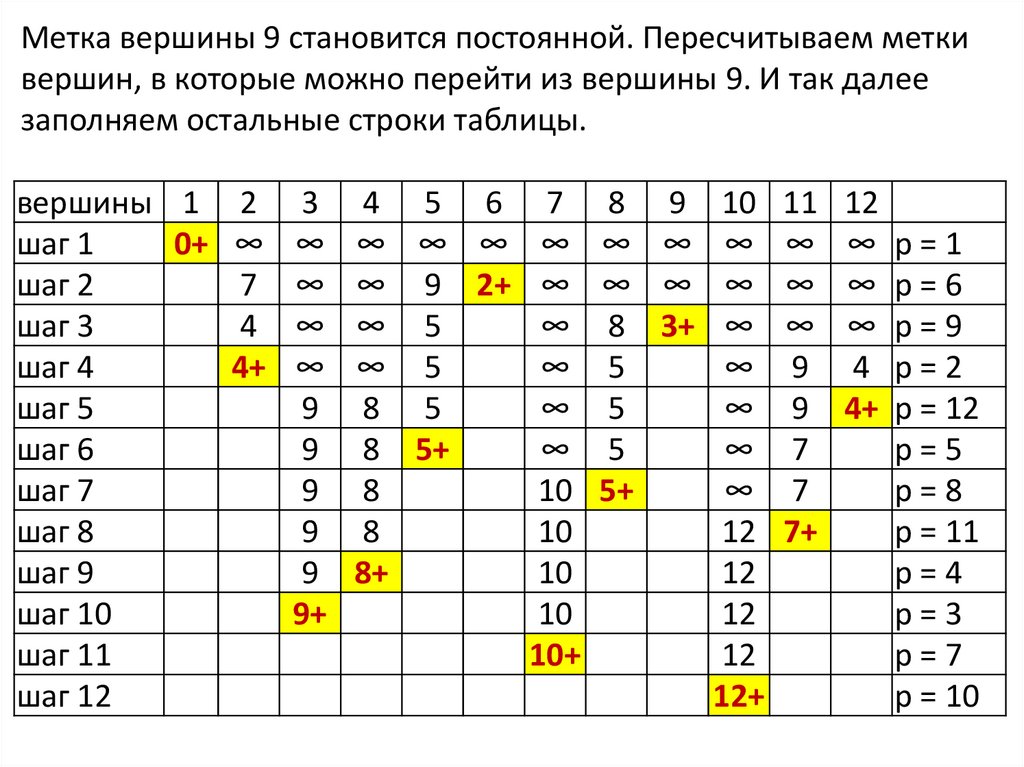
Метка вершины 9 становится постоянной. Пересчитываем меткивершин, в которые можно перейти из вершины 9. И так далее
заполняем остальные строки таблицы.
вершины 1 2
шаг 1
0+ ∞
шаг 2
7
шаг 3
4
шаг 4
4+
шаг 5
шаг 6
шаг 7
шаг 8
шаг 9
шаг 10
шаг 11
шаг 12
3
∞
∞
∞
∞
9
9
9
9
9
9+
4 5 6 7 8 9 10 11 12
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ p=1
∞ 9 2+ ∞ ∞ ∞ ∞ ∞ ∞ p = 6
∞ 5
∞ 8 3+ ∞ ∞ ∞ p = 9
∞ 5
∞ 5
∞ 9 4 p=2
8 5
∞ 5
∞ 9 4+ p = 12
8 5+
∞ 5
∞ 7
p=5
8
10 5+
∞ 7
p=8
8
10
12 7+
p = 11
8+
10
12
p=4
10
12
p=3
10+
12
p=7
12+
p = 10
17.
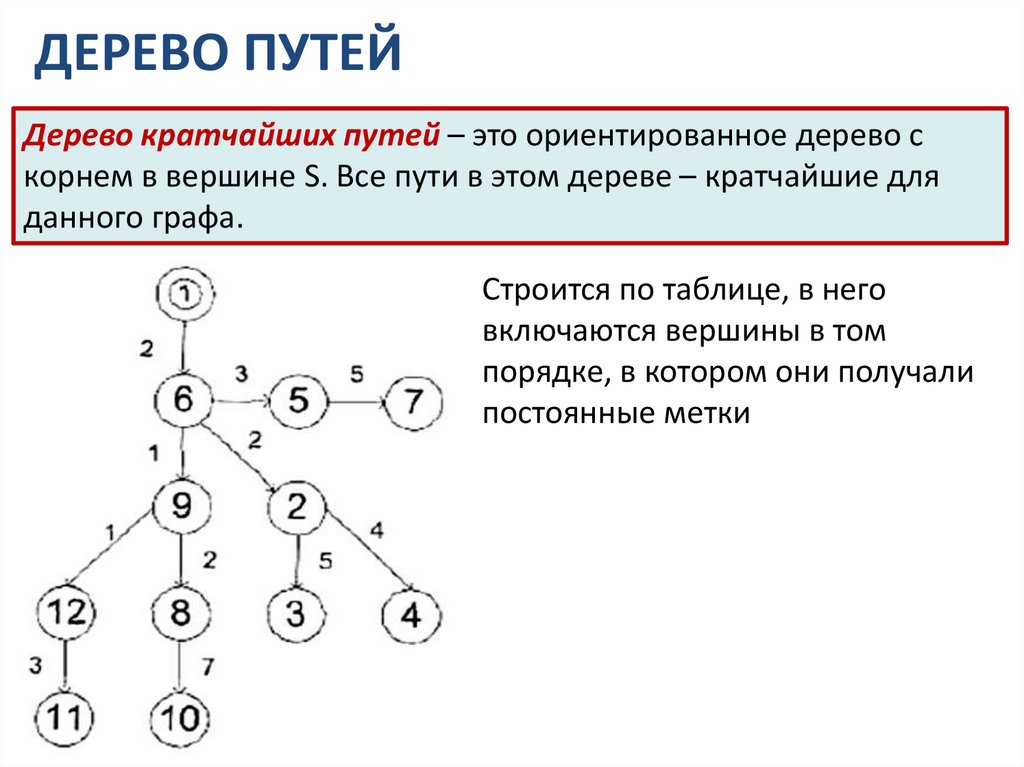
ДЕРЕВО ПУТЕЙДерево кратчайших путей – это ориентированное дерево с
корнем в вершине S. Все пути в этом дереве – кратчайшие для
данного графа.
Строится по таблице, в него
включаются вершины в том
порядке, в котором они получали
постоянные метки










 mathematics
mathematics








