Математические схемы моделирования

1.

Математические схемы
моделирования

2.

Математическая модель
• В общем случае математическую модель любой
динамической системы можно представить в
следующем виде:
y( t ) F(x,h ,t)
где - x совокупность входных воздействий на
систему,
- h совокупность внутренних параметров системы,
- y совокупность выходных характеристик
системы,
F - закон функционирования системы.

3.

Основные подходы
При построении математических моделей
процессов функционирования систем можно
выделить следующие основные подходы:
• непрерывно-детерминированный;
• дискретно-детерминированный;
• дискретно-стохастический;
• непрерывно-стохастический;
• Сетевой;
• обобщенный (или универсальный).
Соответственно этим подходам были
разработаны типовые математические схемы
создания моделей.

4.

Математическая схема
• Математическая схема – это звено
при переходе от содержательного к
формальному описанию процесса
функционирования системы с учётом
воздействия внешней среды
• Типовые математические схемы:
• D–схемы, F–схемы, P–схемы, Q–схемы
и A–схемы.

5.

D–схемы
• 1. Непрерывно-детерминированный
подход использует в качестве
математических моделей системы
дифференциальных уравнений.
• отсутствие случайностей при работе и
управлении объектом моделирования;
• - явления в объектах моделирования
рассматривают как непрерывные процессы,
то есть те, в которых основная переменная,
часто это время, является непрерывной
величиной.

6.

• Модели построенные по этой схеме
чаще всего ориентированы на изучение
динамики рассматриваемого объекта
(отсюда и название Д-схема). Поэтому
характерным примером использования
такого рода схемы являются
дифференциальные уравнения.
• Например, процесс малых колебаний
маятника описывается обыкновенным
дифференциальным уравнением:

7.

D–схемы
2
d
(t )
2
m l
m g l (t ) 0
2
dt
• Где m и l - масса и длина подвеса
маятника;
• g - ускорение свободного падения;
• ( t ) - угол отклонения маятника в
момент времени t.

8.

F - схемы
• Дискретно-детерминированный подход
реализуется с помощью математического
аппарата теории автоматов.
• Для модели данного класса характерны два
свойства:
• полное отсутствие случайностей
(детерминированность).
• рассмотрение явлений в объекте
моделирования как изменяющихся во
времени процессов (пошагово, т.е.
дискретно.

9.

F - схемы
• Математической моделью при этом подходе
является конечный автомат,
характеризующийся конечным множеством X
входных сигналов, конечным множеством Y
выходных сигналов, конечным множеством Н
внутренних состояний, начальным состоянием
h0 h; функцией переходов g(h,x); функцией
выходов v(h,x). Автомат функционирует в
дискретном автоматном времени, моментами
которого являются такты (примыкающие друг к
другу равные интервалы времени, каждому из
которых соответствуют постоянные значения
входного и выходного сигналов и внутренние
состояния).

10.

• Например: Контроллер в
определенные моменты времени
(такты) считывает информацию с
датчика и выдает управляющее
воздействие. Как только с датчика
придет вторая 1 (подряд или нет не
имеет значения). Он выдаст 1 (управл.
возд.) и будет выдавать 1 до тех пор
пока опять на придет 0.
• X {00010001110} входное множество
• Y {00000001110} выходное множество

11.

Существует несколько способов задания
работы F-автоматов, но наиболее
часто используются:
• табличный;
• графический;
• матричный.

12.

Дискретно-стохастические
модели (Р-схемы)
• P-схема ориентирована на объекты, для
которых характерно случайное
поведение. Для построения математической
модели вероятностного автомата
необходимо описать законы распределения
тех его сторон, которые характеризуются
стохастичностью. Обычно это вероятности
перехода из одного возможного состояния в
другое. (Например Марковские процессы)

13.

Непрерывно-стохастические модели
(Q–схемы)
• Q–схемы применяются в качестве типовых
математических схем систем массового
обслуживания
• Характерным для работы подобных объектов
является стохастический характер процесса
их функционирования, проявляющийся:
• в случайном появлении заявок (требований)
на обслуживание;
• в завершении обслуживания в случайные
моменты времени.

14.

• Элементы СМО.
• 1. Средства обслуживания –
обслуживающие аппараты (ОА) или
каналы обслуживания (К). Средства
обслуживания являются статическими
элементами Q–схем.
• 2. Обслуживаемые заявки – транзакты.
Являются динамическими элементами
Q–схем.
• 3. Очереди.

15.

Состояние СМО
характеризуется:
• 1. Состояниями всех обслуживающих
аппаратов, каждый из которых может
находиться в состоянии “занят” или
“свободен”.
• 2. Состояниями всех транзактов, каждый из
которых может находиться в состоянии
“обслуживание” или “ожидание”.
• 3. Состояниями всех очередей к
обслуживающим аппаратам, определяемыми
количеством находящихся в них транзактов.

16.

Переменные СМО. Переменные величины
разделяются на независимые и системные.
• Независимые величины СМО
характеризуются двумя случайными
переменными:
• а) интервал прибытия – интервал
времени между последовательными
моментами прибытия заявок в систему;
• б) время обслуживания – время,
требуемое обслуживающему аппарату
для выполнения обслуживания.

17.

• Системные величины СМО являются
предметом исследования системы и
назначаются исследователем, например:
• а) число заявок, прибывших на обслуживание
за заданный промежуток времени;
• б) число заявок, которые попали на
обслуживание сразу же по прибытии;
• в) среднее время пребывания заявок в
очереди;
• г) средние длины очередей;
• д) максимальная длина очереди;
• е) нагрузка обслуживающего аппарата

18.

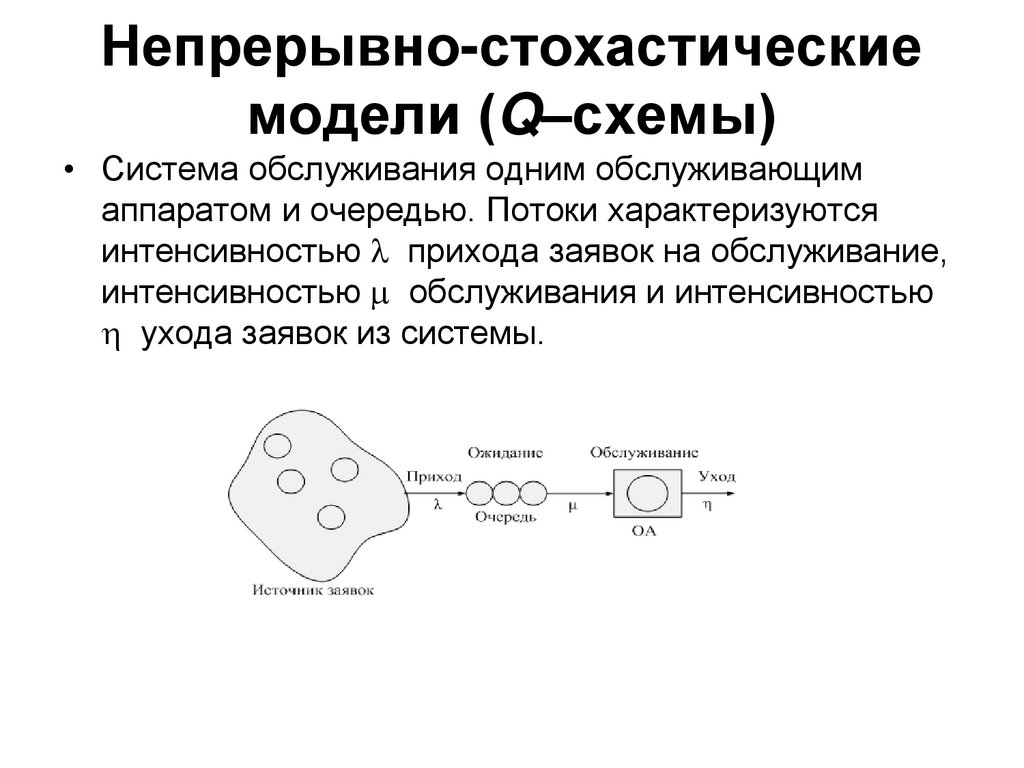
Непрерывно-стохастические
модели (Q–схемы)
• Система обслуживания одним обслуживающим
аппаратом и очередью. Потоки характеризуются
интенсивностью прихода заявок на обслуживание,
интенсивностью обслуживания и интенсивностью
ухода заявок из системы.

19.

Символика Q–схем
Источник заявок;
Материальные потоки (движение
транзактов);
Информационные потоки
Клапан;
Накопитель;
Канал обслуживания;
Узел

20.

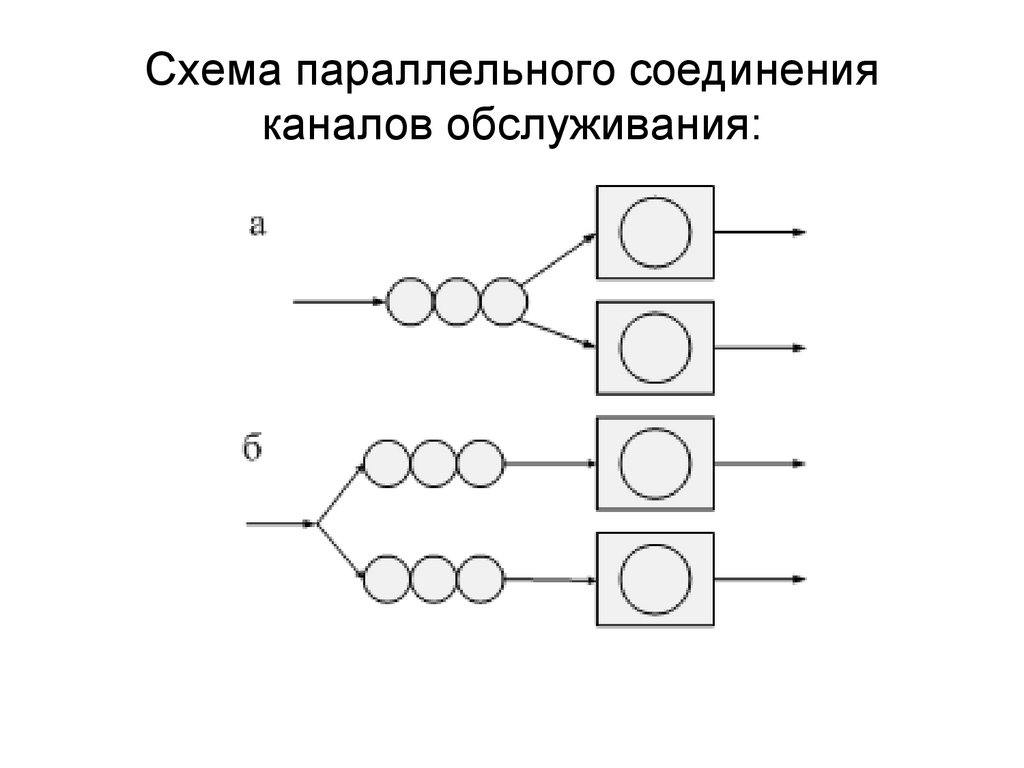
Схема параллельного соединения
каналов обслуживания:

21.

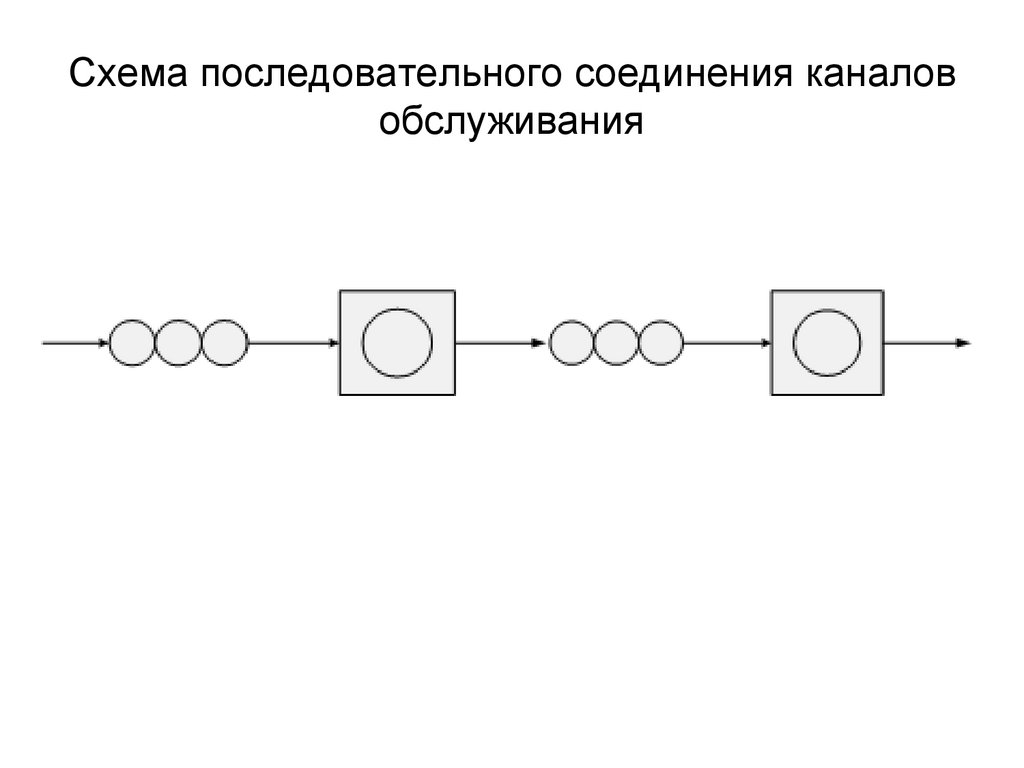
Схема последовательного соединения каналов
обслуживания

22.

Обобщенный подход (А схемы)
• Рассматриваемая система расчленяется на
отдельные подсистемы (агрегаты) таким
образом, чтобы каждая из них
удовлетворительно описывалась той или
иной типовой схемой.
• Если выделенная подсистема не может быть
удовлетворительно описана типовой схемой,
то она вновь подвергается очередному
разбиению на агрегаты и т.д. Важнейшим
моментом здесь является сохранение и
отображение связей между выделенными
подсистемами.