Similar presentations:
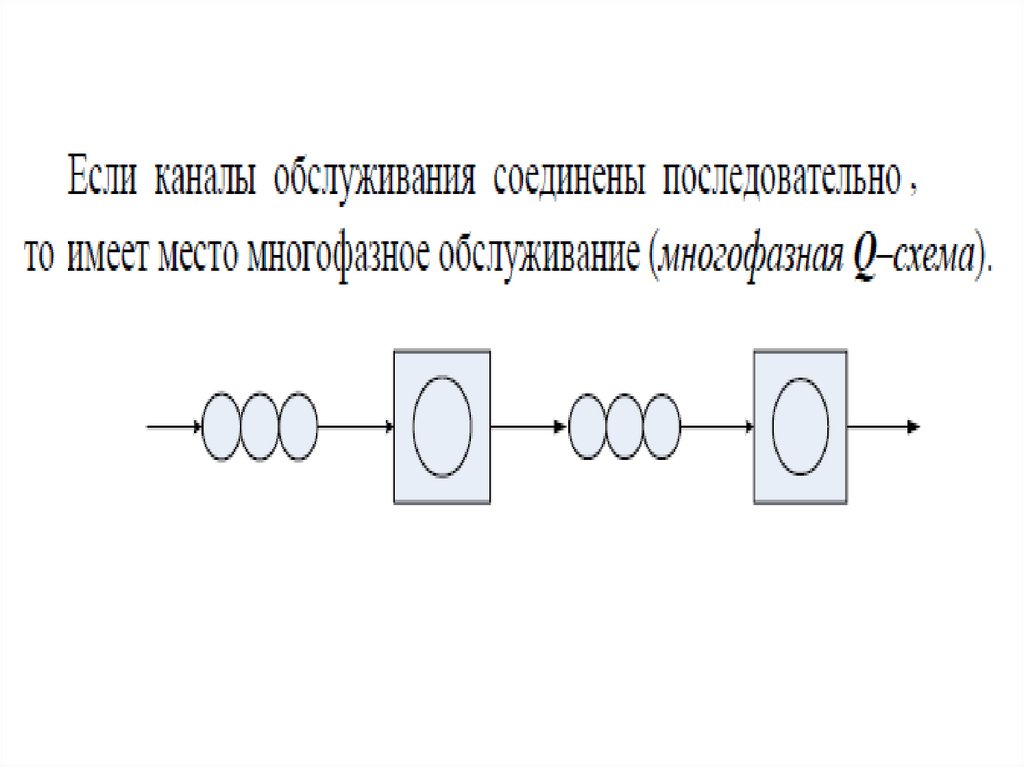
Q - схемы. Непрерывное и стохастическое
1.
Q-схемыНепрерывное
и
стохастическое
2.
3.
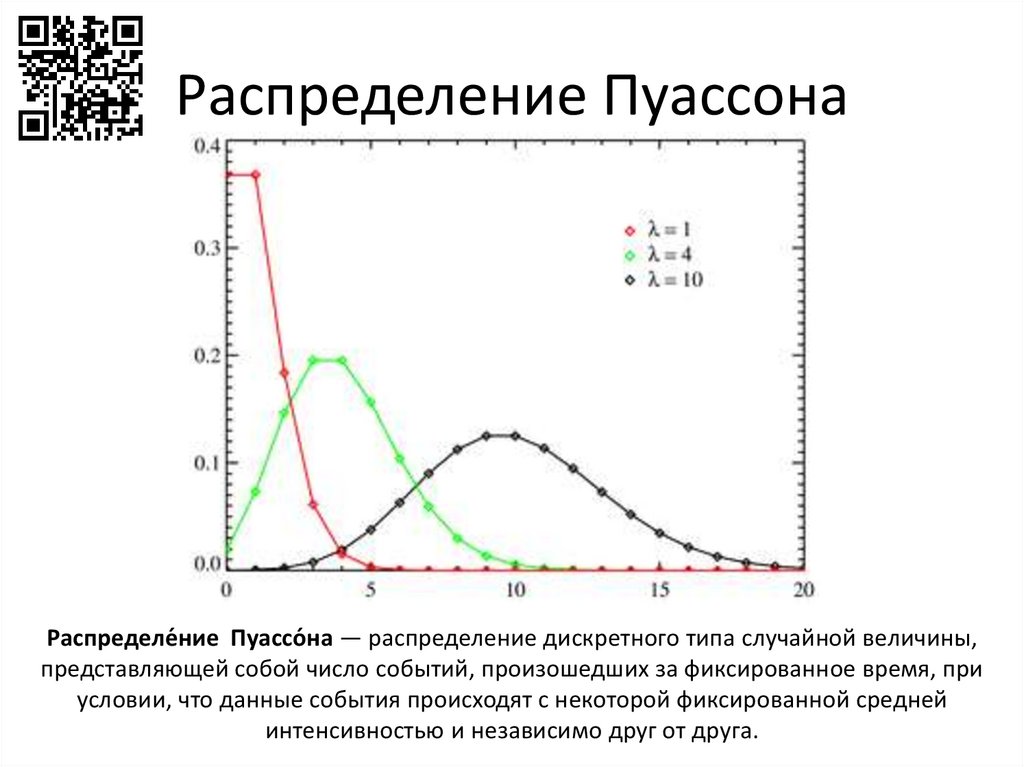
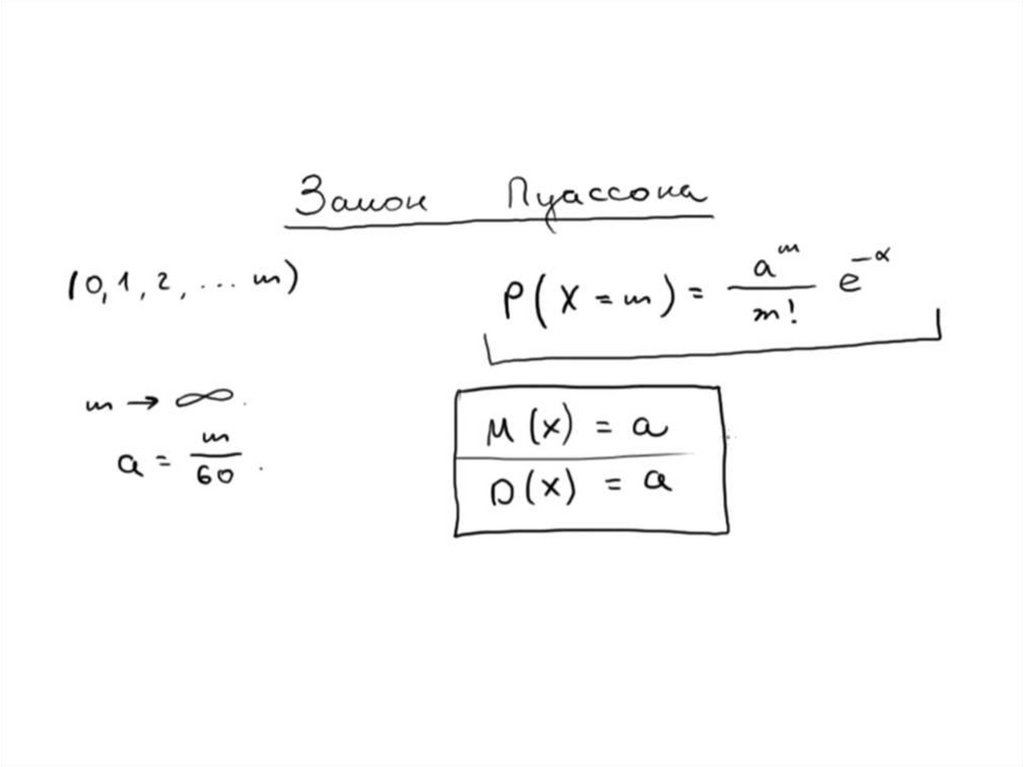
Распределение ПуассонаРаспределе́ние Пуассо́на — распределение дискретного типа случайной величины,
представляющей собой число событий, произошедших за фиксированное время, при
условии, что данные события происходят с некоторой фиксированной средней
интенсивностью и независимо друг от друга.
4.
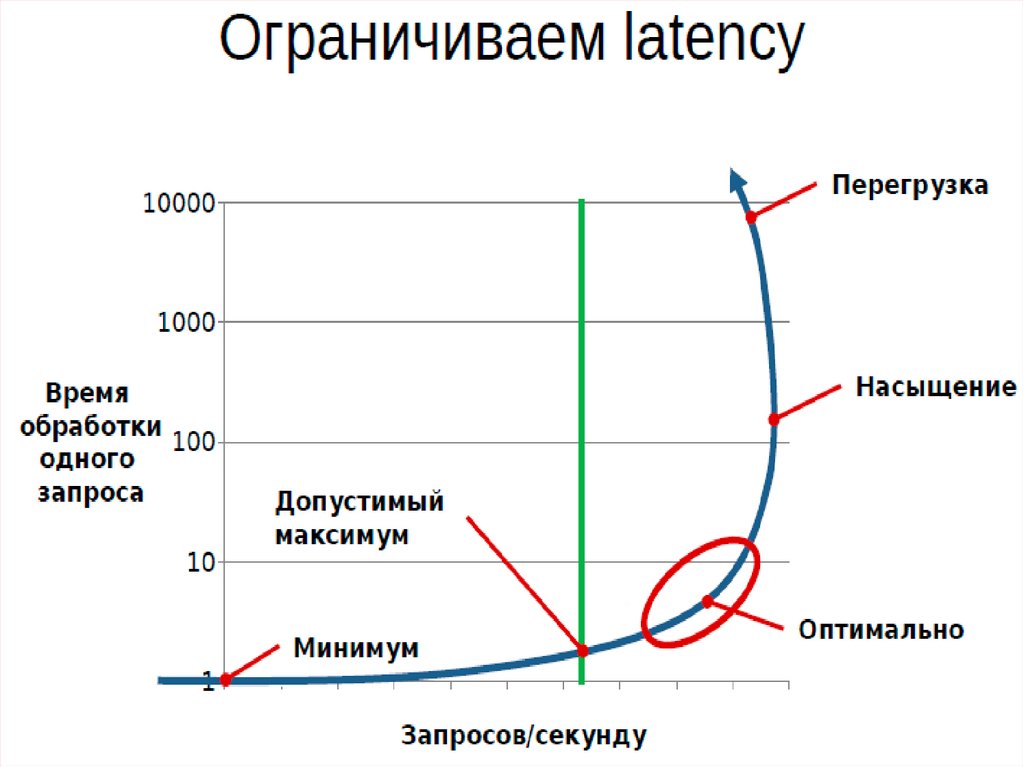
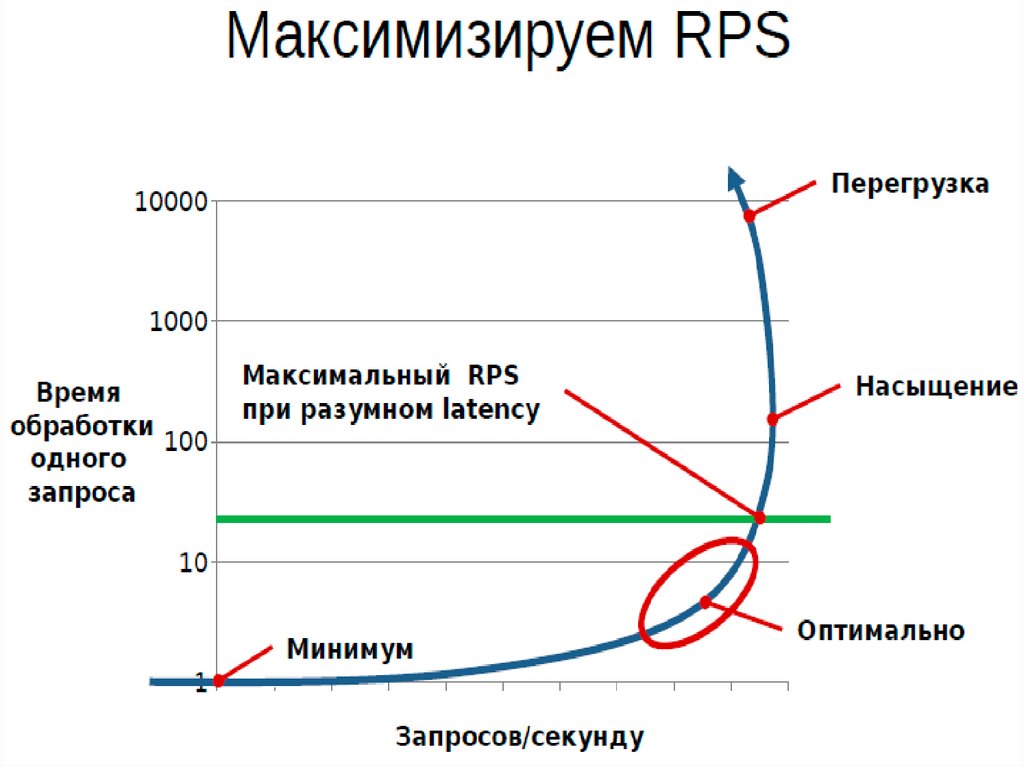
Latency (engineering)Латентность между причиной и
следствием
5.
Теорема ЛиттлаДолгосрочное среднее
количество L требований в стационарной
системе равно долгосрочной средней
интенсивности λ входного потока,
умноженной на среднее
время W пребывания заявки в системе.
L = λW
6.
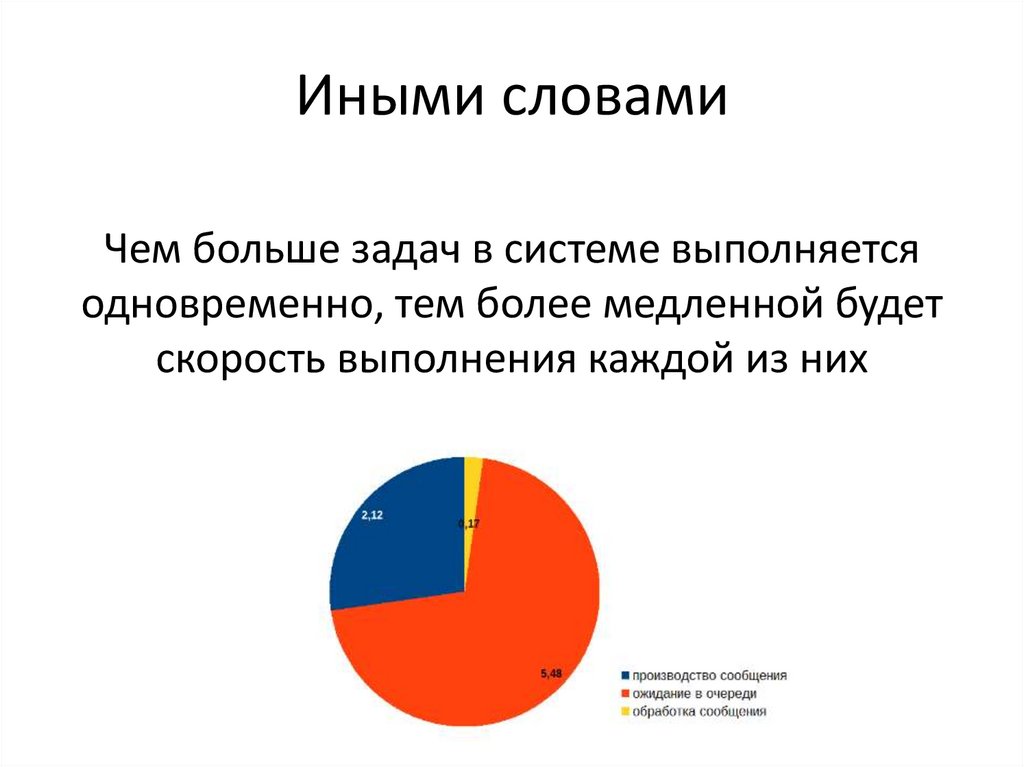
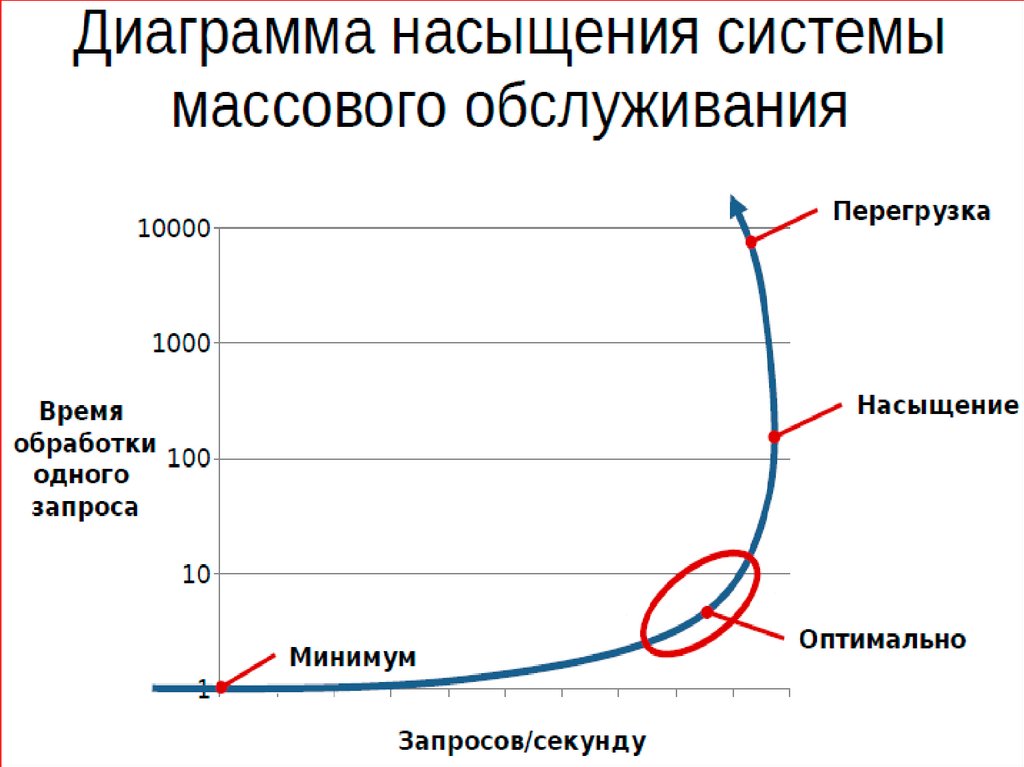
Иными словамиЧем больше задач в системе выполняется
одновременно, тем более медленной будет
скорость выполнения каждой из них
7.
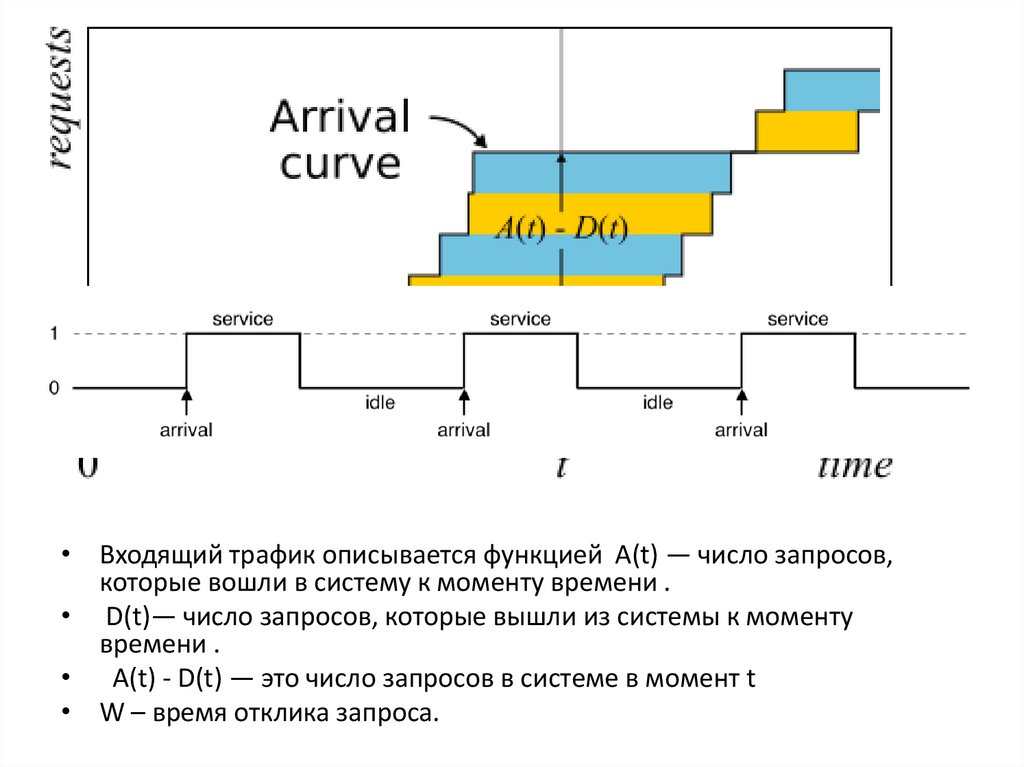
• Входящий трафик описывается функцией A(t) — число запросов,которые вошли в систему к моменту времени .
• D(t)— число запросов, которые вышли из системы к моменту
времени .
• A(t) - D(t) — это число запросов в системе в момент t
• W – время отклика запроса.
8.
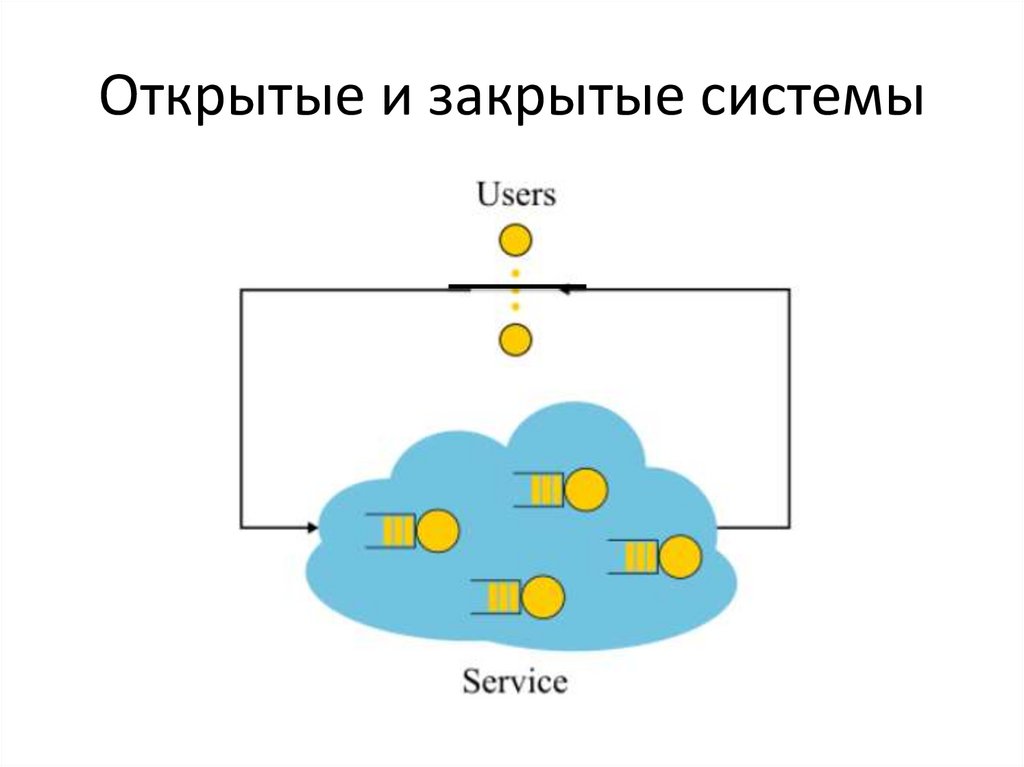
Открытые и закрытые системы9.
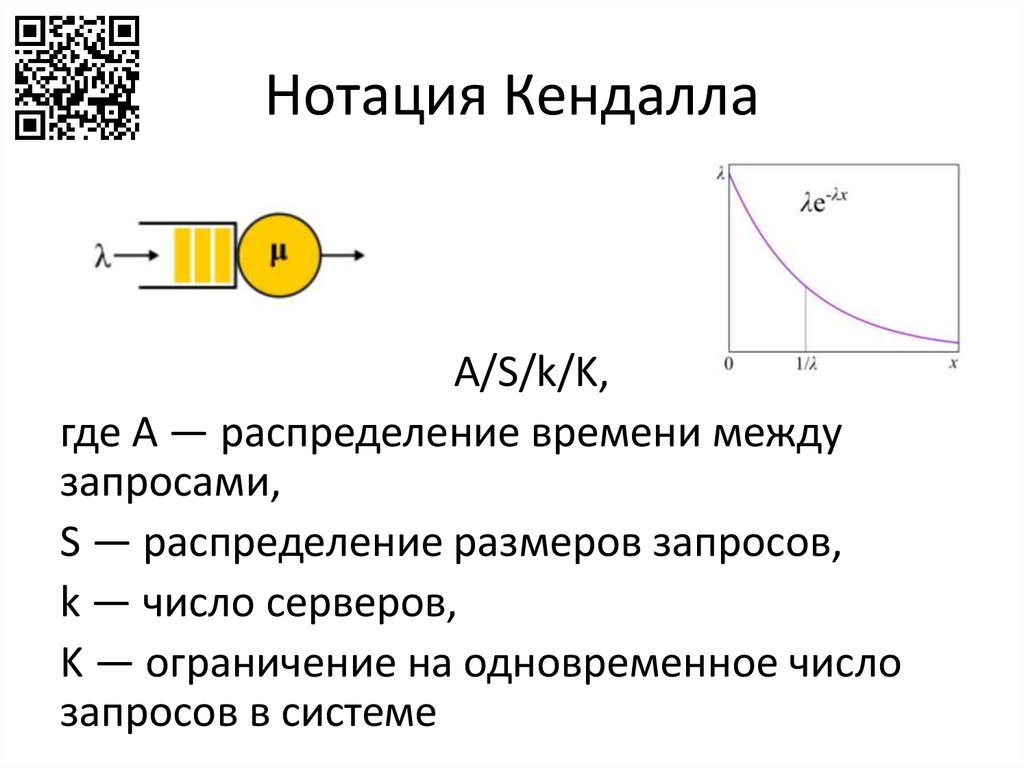
Нотация КендаллаA/S/k/K,
где A — распределение времени между
запросами,
S — распределение размеров запросов,
k — число серверов,
K — ограничение на одновременное число
запросов в системе
10.
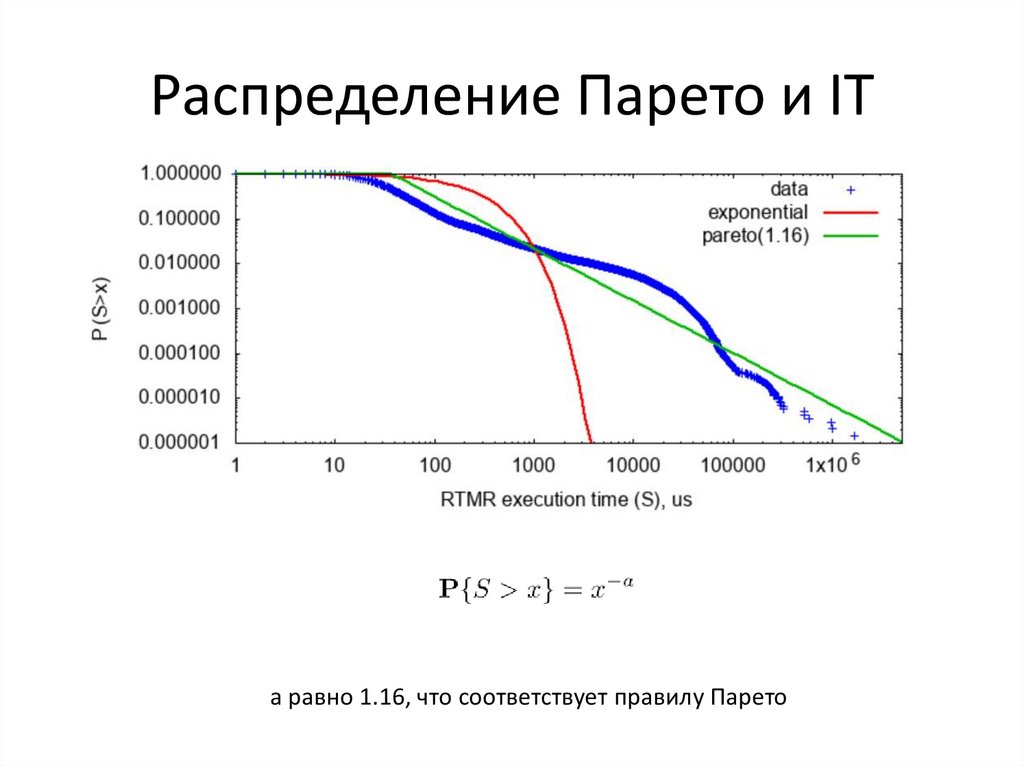
Распределение Парето и ITa равно 1.16, что соответствует правилу Парето
11.
«НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕМОДЕЛИ
(Q-СХЕМЫ)»
12.
13.
14.
15.
16.
17.
18.
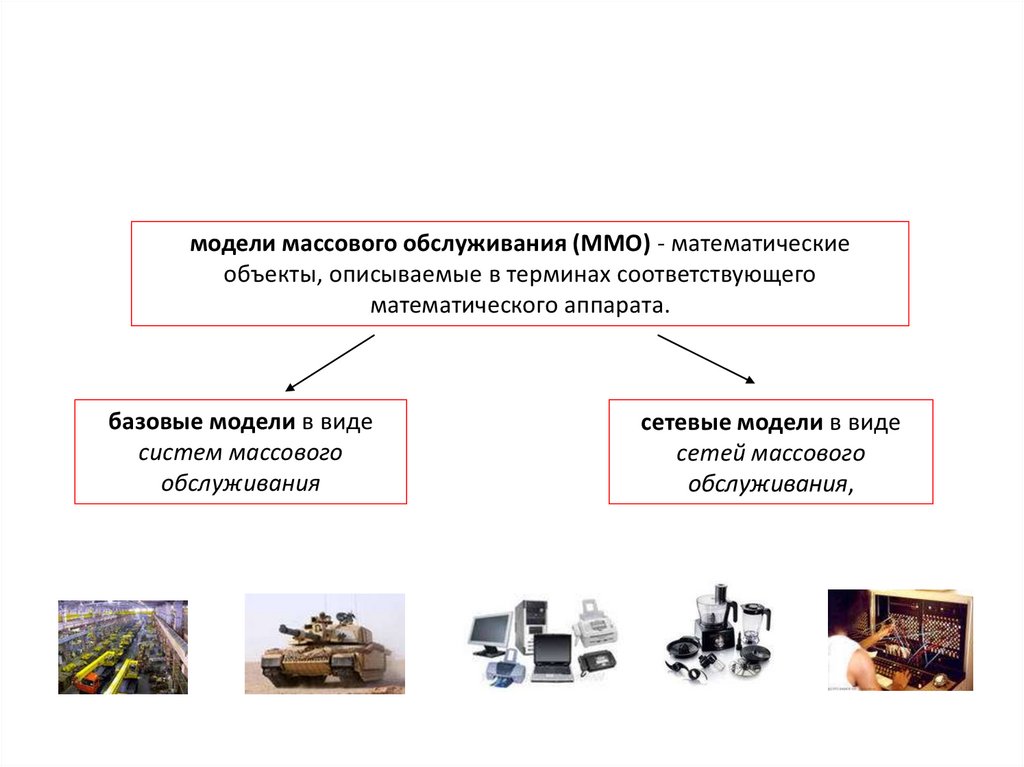
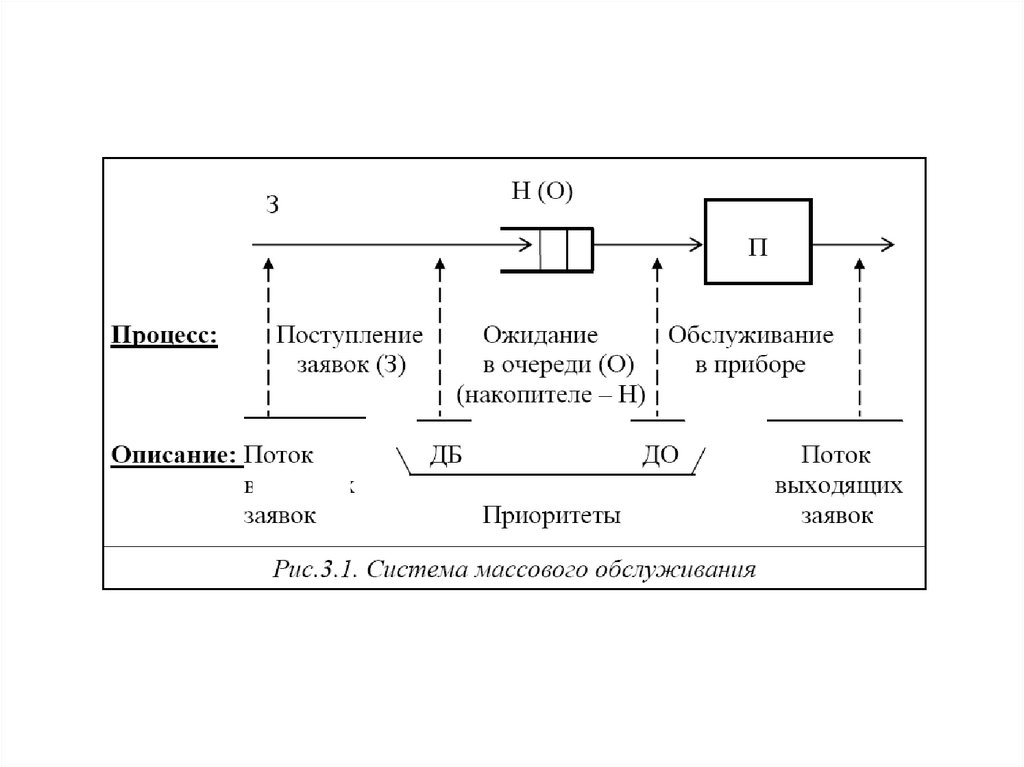
модели массового обслуживания (ММО) - математическиеобъекты, описываемые в терминах соответствующего
математического аппарата.
базовые модели в виде
систем массового
обслуживания
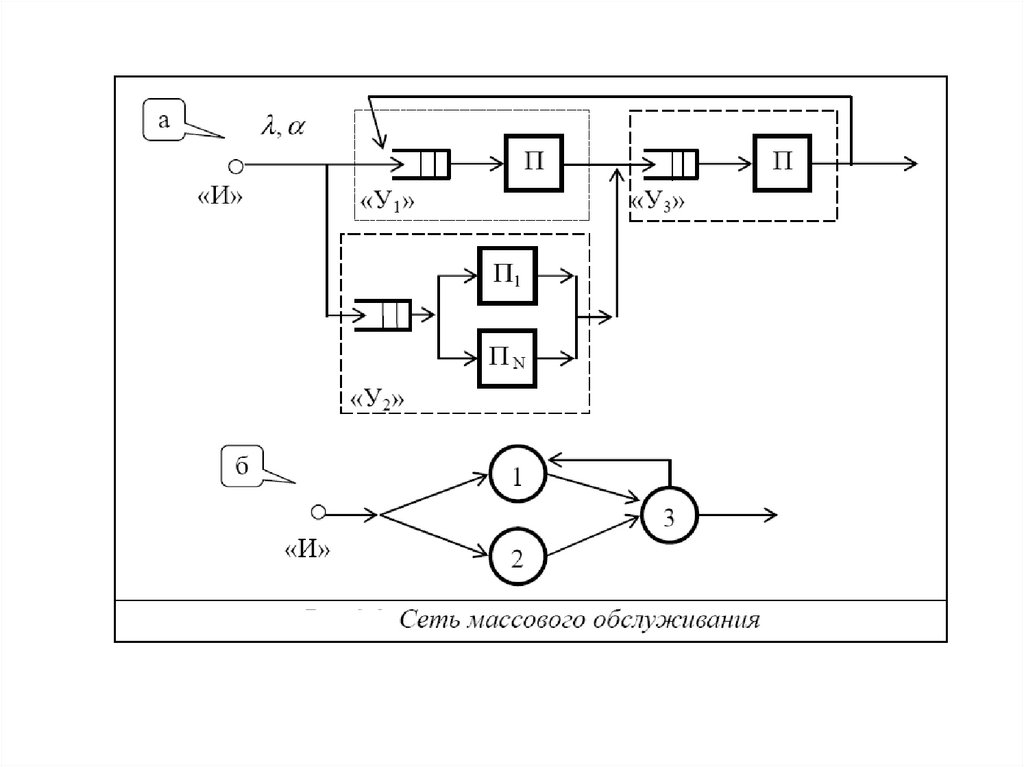
сетевые модели в виде
сетей массового
обслуживания,
19.
1920.
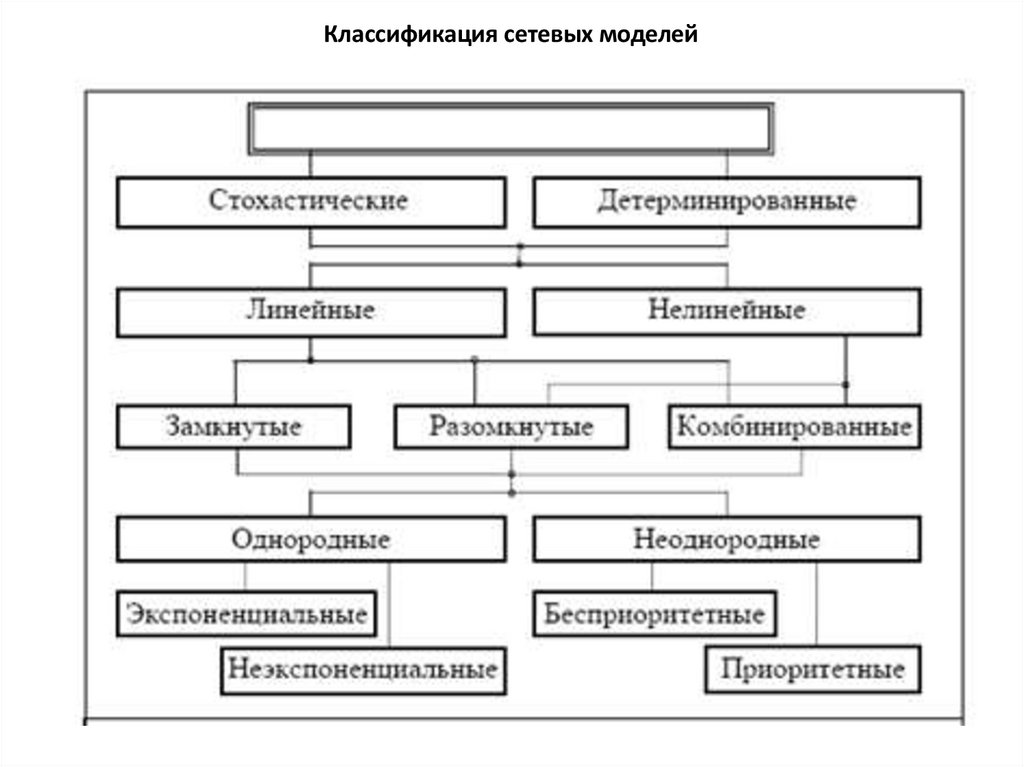
Классификация сетевых моделей20
21.
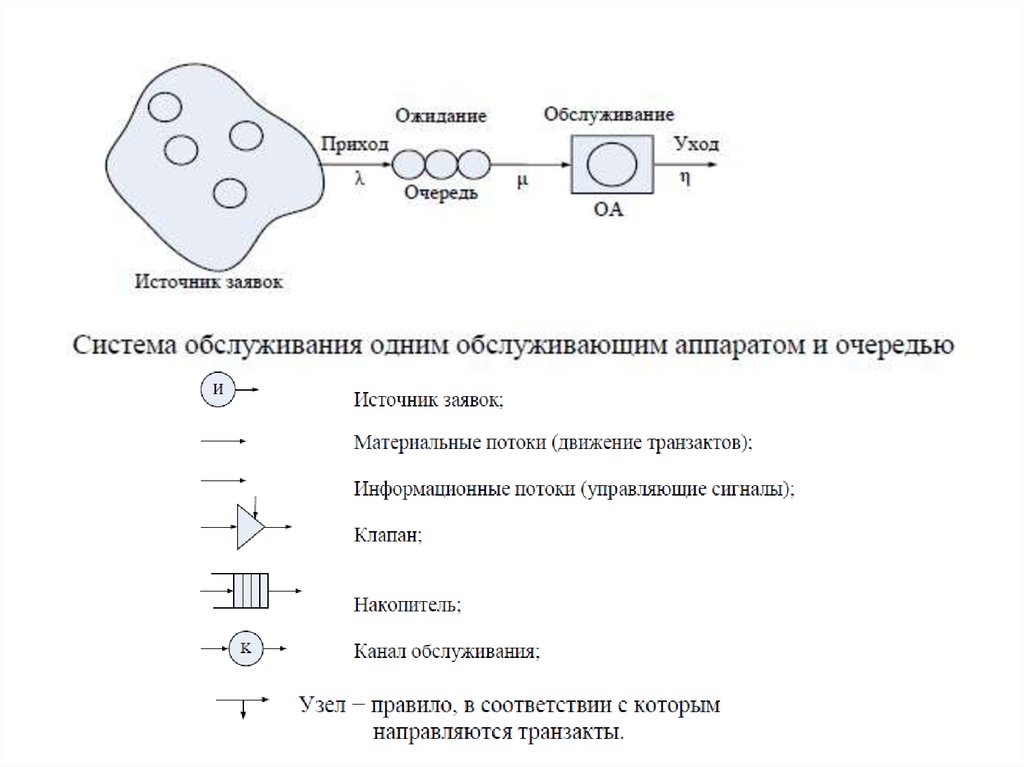
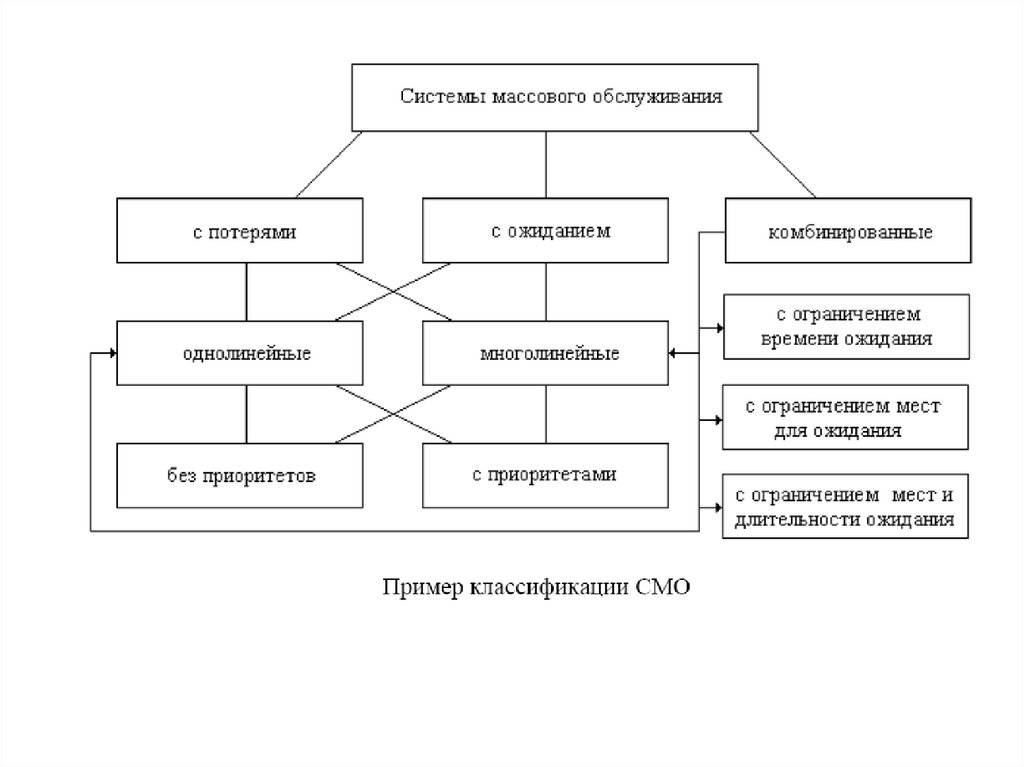
Системы массового обслуживания (СМО) системы специального вида, реализующие многократное выполнениеоднотипных задач.
22.
Задача: Какое количество телефонисток (приусловии их полной занятости) должно работать на
станции для того, чтобы потери требований были
минимальными.
Задача:
Определить
количество
врачей,
вспомогательного персонала, автомашин, для того
чтобы время ожидания вызова было для больных
оптимальным при условии минимизации затрат
на эксплуатацию системы и максимизации
качества обслуживания.
Задача: Обеспечить определенный объем
перевозок при минимальных расходах. При
этом сократить простои судов при погрузочноразгрузочных работах.
Задача: Обеспечить ускорение обработки
сигналов при заданной суммарной длине
очереди.
23.
24.
25.
«МАТЕМАТИЧЕСКИЕ МОДЕЛИПОТОКОВ СОБЫТИЙ»
1. Поток заявок
2. Свойства простейшего пуассоновского потока
3. Длительность обслуживания заявок
4. Стратегии управления потоками заявок
5. Простейший поток и решение практических задач.
26.
27.
28.
29.
30.
31.
1. Вероятность – численная мера степени объективной возможностинекоторого события. Вероятность может принимать только положительные
значения из интервала [0; 1].
Величина, принимающая значение, неизвестное заранее, называется
случайной. Различают дискретные (прерывные) и непрерывные
(аналоговые) случайные величины.
2. Закон распределения случайной величины – соотношение,
устанавливающее связь между возможными значениями случайной
величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины может быть
задан:
· аналитически в виде математического выражения;
· таблично в виде ряда распределения;
· графически в виде многоугольника распределения.
Закон распределения непрерывной случайной величины может быть
задан в виде:
· функции распределения F(x) случайной величины X, представляющей собой вероятность того, что случайная величина X примет значение
меньшее, чем некоторое заданное значение x: F(x) = P(X < x);
· плотности распределения f(x), определяемой как производная от
функции распределения F(x) по x: f (x) = F¢(x).
32.
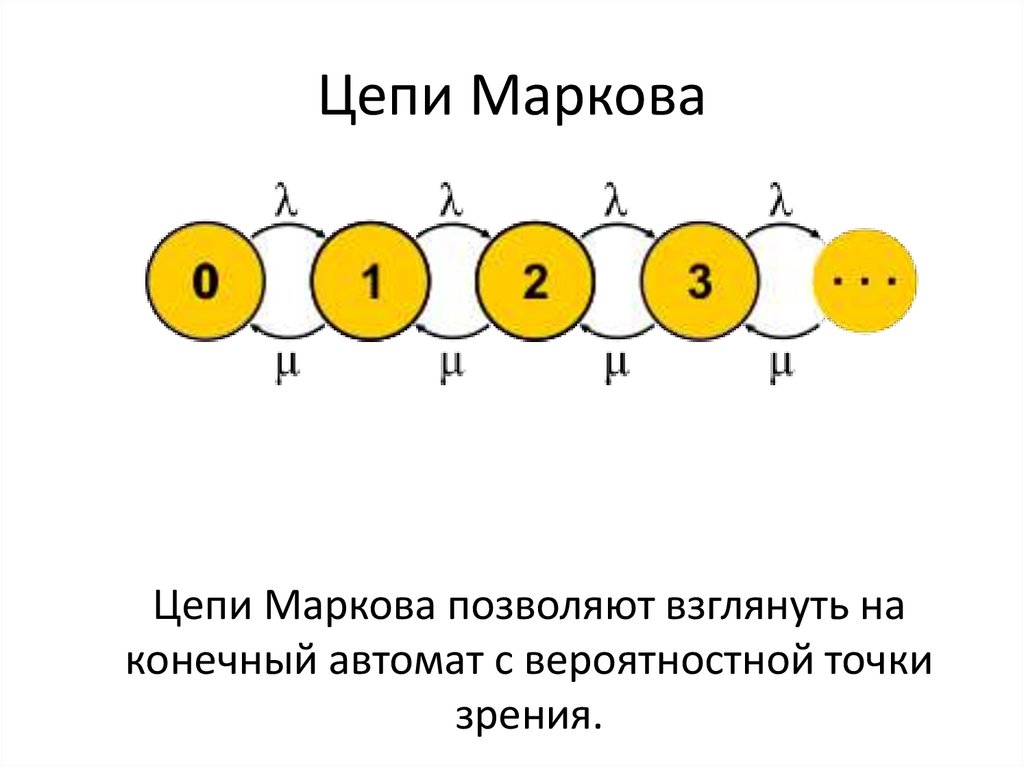
Цепи МарковаЦепи Маркова позволяют взглянуть на
конечный автомат с вероятностной точки
зрения.
33.
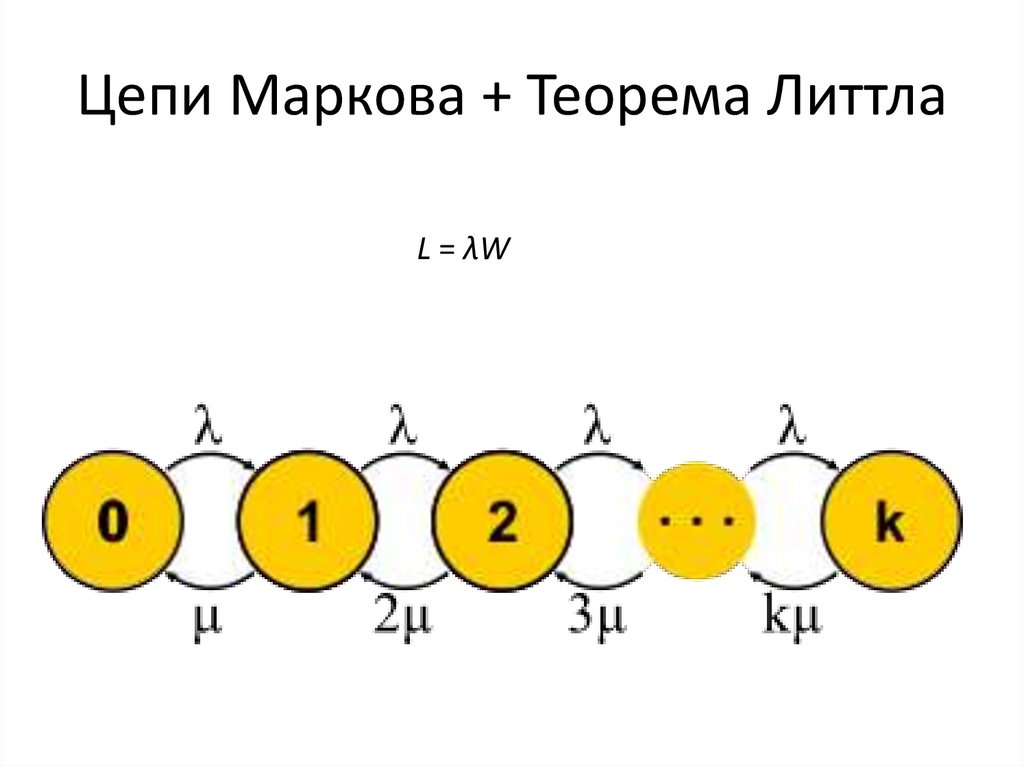
Цепи Маркова + Теорема ЛиттлаL = λW
34.
35.
36.
«Параметры ихарактеристика систем и
сетей массового
обслуживания»
37.
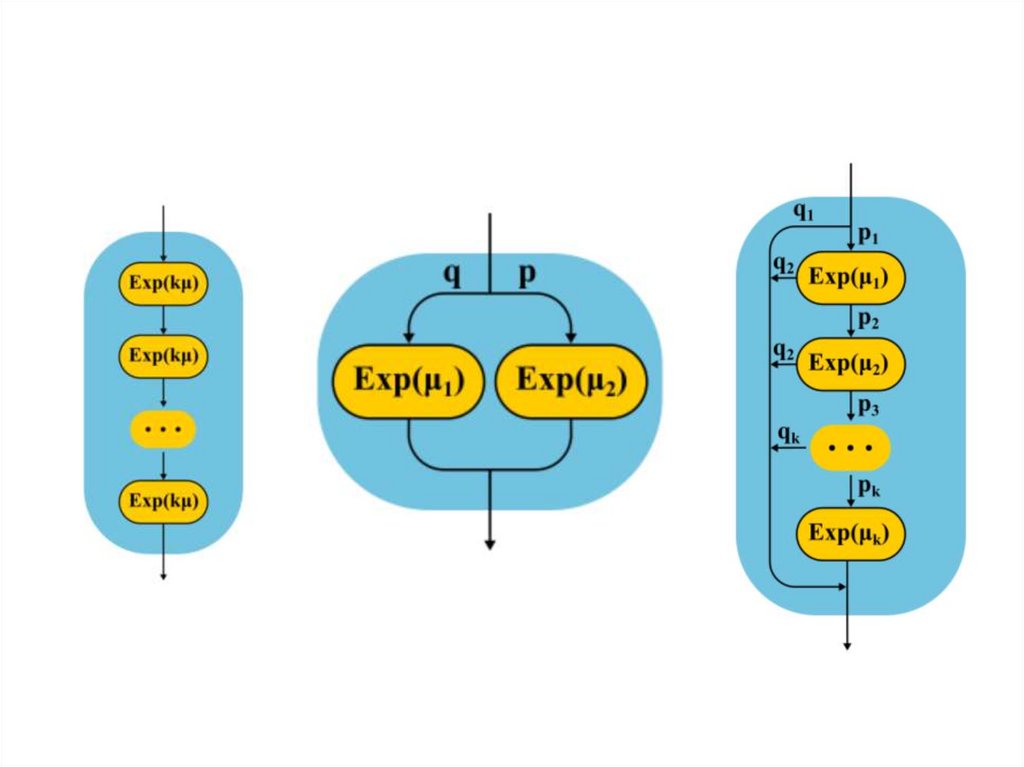
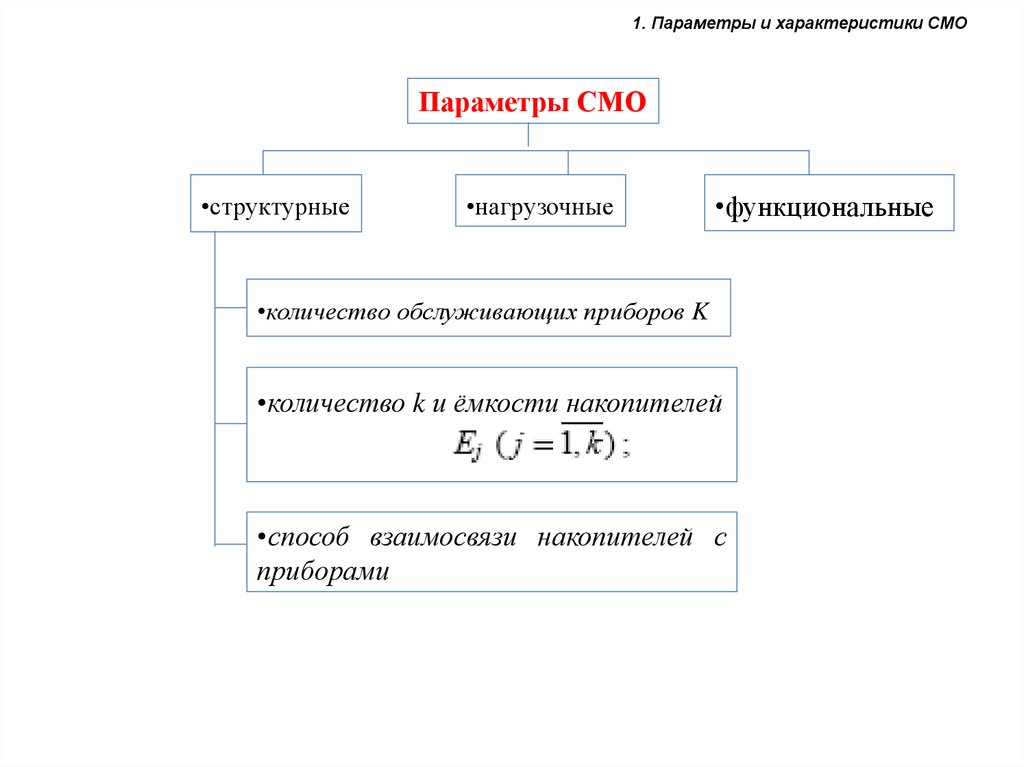
1. Параметры и характеристики СМОПараметры СМО
•структурные
•нагрузочные
•функциональные
•количество обслуживающих приборов K
•количество k и ёмкости накопителей
•способ взаимосвязи накопителей с
приборами
38.
1. Параметры и характеристики СМОПараметры СМО
•структурные
•нагрузочные
•функциональные
•количество поступающих в систему классов
заявок H
•закон распределения
интервалов
времени между поступающими в систему
заявками класса
, или первые два
момента распределения, задаваемые,
например, в виде интенсивности λi и
коэффициента вариации интервалов
•закон распределения
длительности
обслуживания заявок класса
или, как минимум, первые два момента
распределения, в качестве которых обычно
используются средняя длительность
или интенсивность
обслуживания и
коэффициент вариации
39.
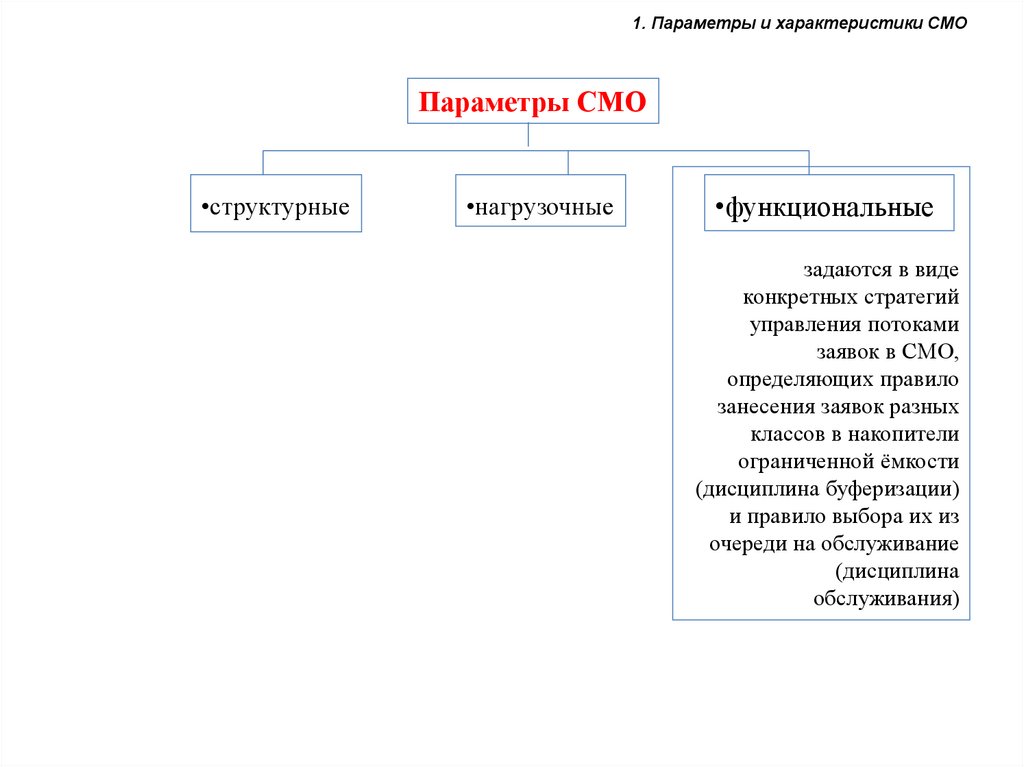
1. Параметры и характеристики СМОПараметры СМО
•структурные
•нагрузочные
•функциональные
задаются в виде
конкретных стратегий
управления потоками
заявок в СМО,
определяющих правило
занесения заявок разных
классов в накопители
ограниченной ёмкости
(дисциплина буферизации)
и правило выбора их из
очереди на обслуживание
(дисциплина
обслуживания)
40.
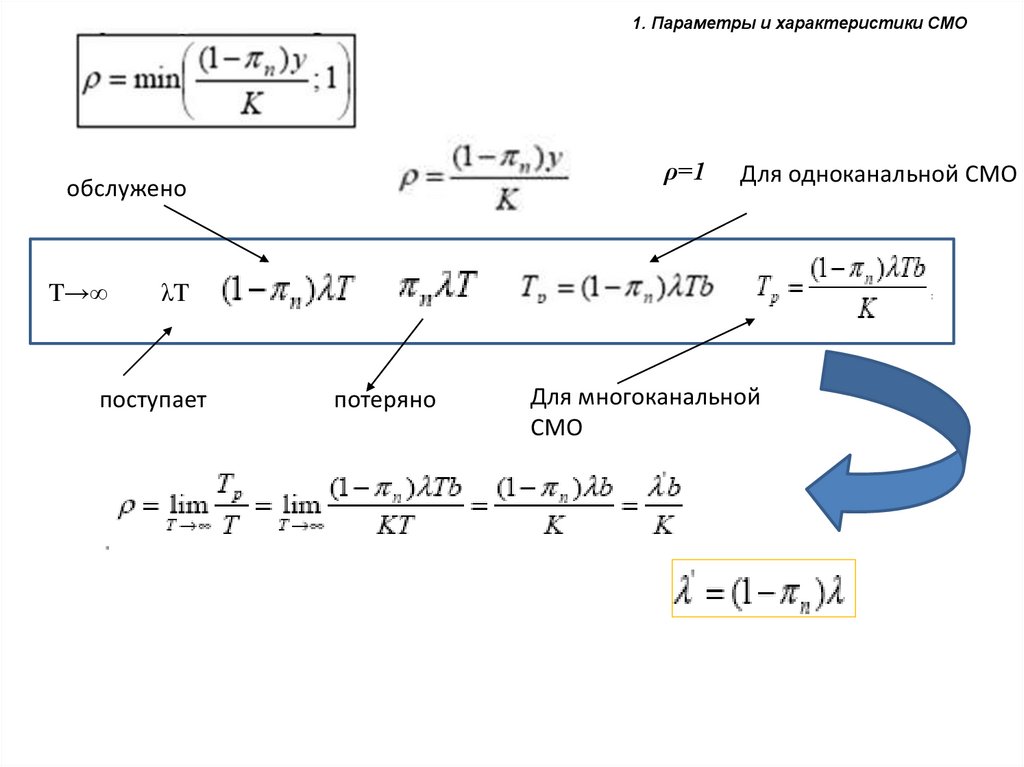
1. Параметры и характеристики СМОρ=1
обслужено
T→∞
Для одноканальной СМО
λT
поступает
потеряно
Для многоканальной
СМО
40
41.
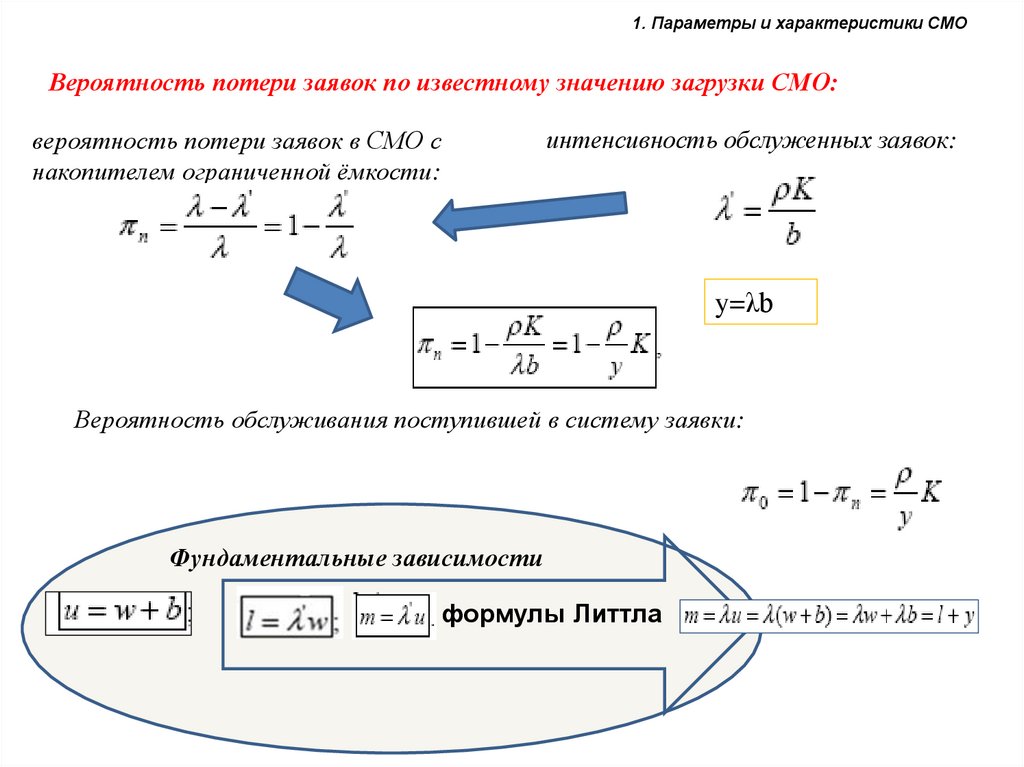
1. Параметры и характеристики СМОВероятность потери заявок по известному значению загрузки СМО:
интенсивность обслуженных заявок:
вероятность потери заявок в СМО с
накопителем ограниченной ёмкости:
y=λb
Вероятность обслуживания поступившей в систему заявки:
Фундаментальные зависимости
формулы Литтла
41
42.
1. Параметры и характеристики СМОХарактеристики СМО с неоднородным потоком заявок
СМО с неоднородным потоком заявок, в которую поступают H классов заявок
с интенсивностями
и средними длительностями обслуживания
характеристики по каждому классу (потоку) заявок;
характеристики объединённого (суммарного) потока заявок
Характеристики по каждому классу заявок
• нагрузка, создаваемая заявками класса
• вероятность потери заявок:
• вероятность обслуживания заявки:
• интенсивность потока обслуженных заявок (производительность по i-му
классу заявок):
• интенсивность потока потерянных заявок:
• загрузка системы, создаваемая заявками класса i:
• время ожидания заявок в очереди: wi
• время пребывания заявок в системе:
• длина очереди заявок:
• число заявок в системе (в очереди и на обслуживании):
42
43.
1. Параметры и характеристики СМОХарактеристики объединённого (суммарного) потока заявок
• суммарная интенсивность поступления заявок в систему
(интенсивность суммарного потока):
• суммарная нагрузка Y и суммарная загрузка R системы:
• коэффициент простоя системы:
• среднее время ожидания W и среднее время пребывания U заявок
объединённого потока в системе:
• суммарная длина очереди и суммарное число заявок в системе:
Фундаментальные соотношения
43
44.
«НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕМОДЕЛИ
(опять)»
45.
1. Одноканальная СМО без накопителя (M/M/1/0)2. Многоканальная СМО без накопителя (M/M/N/0)
3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r)
4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1)
46.
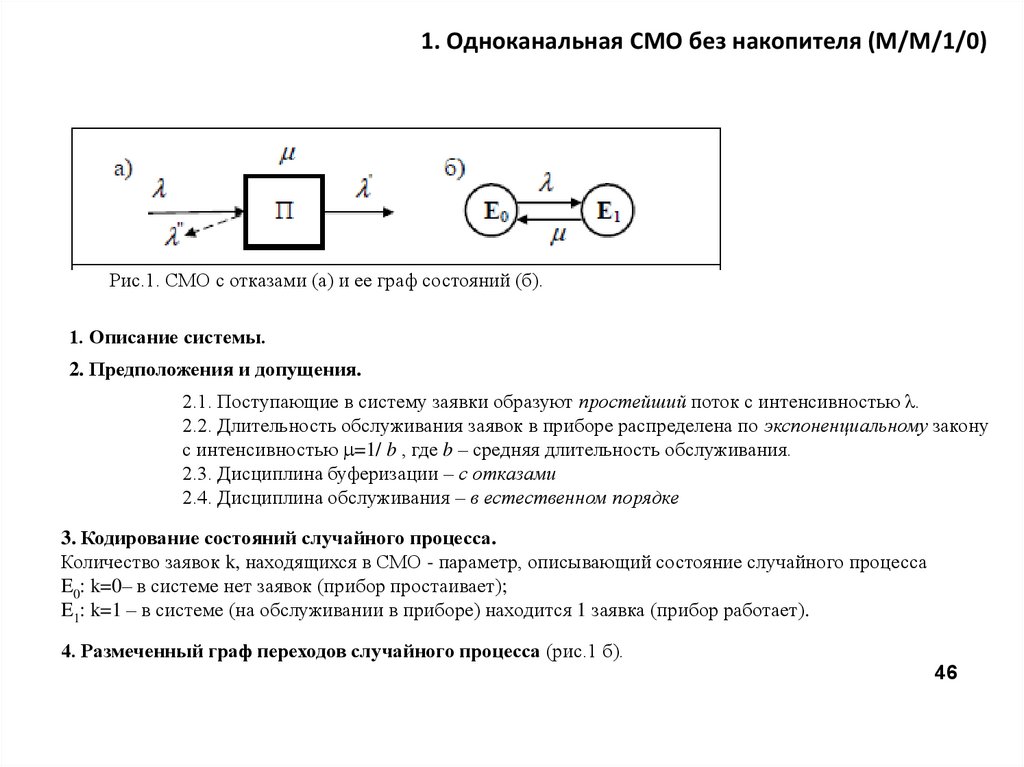
1. Одноканальная СМО без накопителя (M/M/1/0)Рис.1. СМО с отказами (а) и ее граф состояний (б).
1. Описание системы.
2. Предположения и допущения.
2.1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ.
2.2. Длительность обслуживания заявок в приборе распределена по экспоненциальному закону
с интенсивностью =1/ b , где b – средняя длительность обслуживания.
2.3. Дисциплина буферизации – с отказами
2.4. Дисциплина обслуживания – в естественном порядке
3. Кодирование состояний случайного процесса.
Количество заявок k, находящихся в СМО - параметр, описывающий состояние случайного процесса
E0: k=0– в системе нет заявок (прибор простаивает);
E1: k=1 – в системе (на обслуживании в приборе) находится 1 заявка (прибор работает).
4. Размеченный граф переходов случайного процесса (рис.1 б).
46
47.
1. Одноканальная СМО без накопителя (M/M/1/0)5. Диаграммы функционирования системы.
'Рис.2. Диаграммы процессов в СМО с отказами
а) поступления в СМО заявок, интервалы между которыми в случае простейшего потока распределены по
экспоненциальному закону;
б) перехода из состояния Е0 в состояние Е1 и обратно, в которых может находиться система;
в) выхода из системы обслуженных заявок в моменты времени
г) выхода из системы необслуженных заявок, получивших отказ из-за занятости прибора в моменты
времени '
д) формирования интервалов времени между соседними переходами случайного процесса.
47
48.
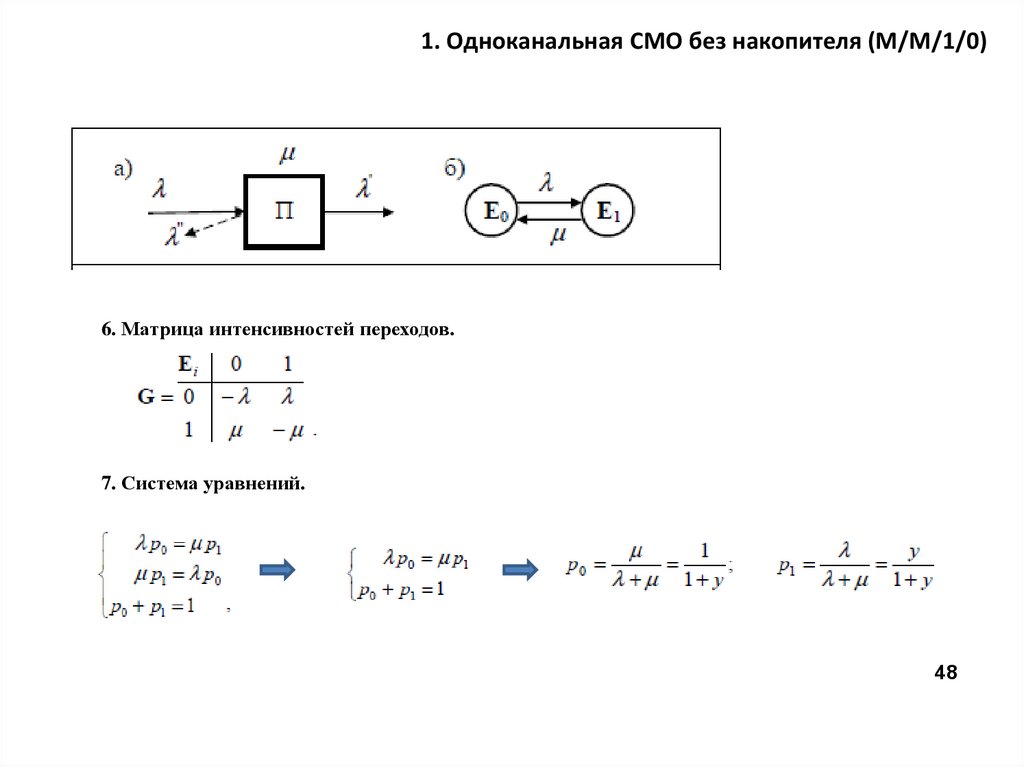
1. Одноканальная СМО без накопителя (M/M/1/0)6. Матрица интенсивностей переходов.
7. Система уравнений.
48
49.
,1. Одноканальная СМО без накопителя (M/M/1/0)
;
8. Расчет характеристик СМО.
1) нагрузка: y=λ/ =λb
2) загрузка определяется как вероятность работы прибора: ρ=p1 и не совпадает с нагрузкой
3) коэффициент простоя системы
4) среднее число заявок в системе: m=p1=ρ
5) вероятность потери заявок в результате отказа в обслуживании из-за занятости прибора
6) производительность системы:
7) интенсивность потока не обслуженных заявок, то есть получивших отказ:
8) среднее время пребывания заявок в системе:
9. Анализ свойств системы.
49
50.
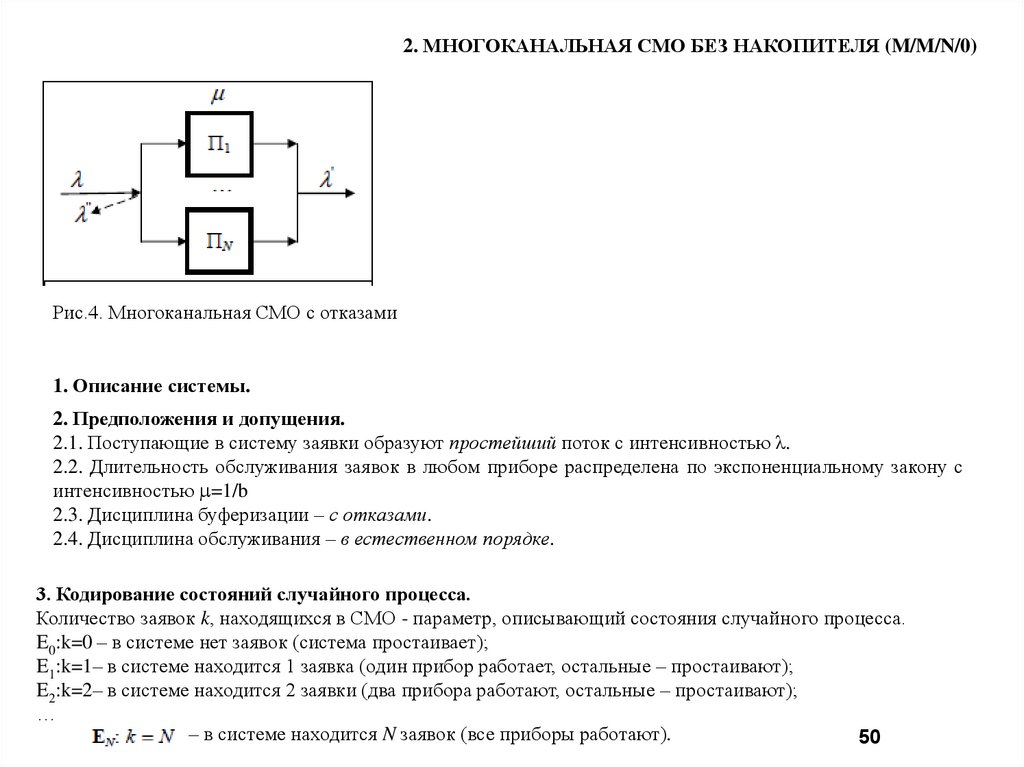
2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0)Рис.4. Многоканальная СМО с отказами
1. Описание системы.
2. Предположения и допущения.
2.1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ.
2.2. Длительность обслуживания заявок в любом приборе распределена по экспоненциальному закону с
интенсивностью =1/b
2.3. Дисциплина буферизации – с отказами.
2.4. Дисциплина обслуживания – в естественном порядке.
3. Кодирование состояний случайного процесса.
Количество заявок k, находящихся в СМО - параметр, описывающий состояния случайного процесса.
E0:k=0 – в системе нет заявок (система простаивает);
E1:k=1– в системе находится 1 заявка (один прибор работает, остальные – простаивают);
E2:k=2– в системе находится 2 заявки (два прибора работают, остальные – простаивают);
…
– в системе находится N заявок (все приборы работают).
50
51.
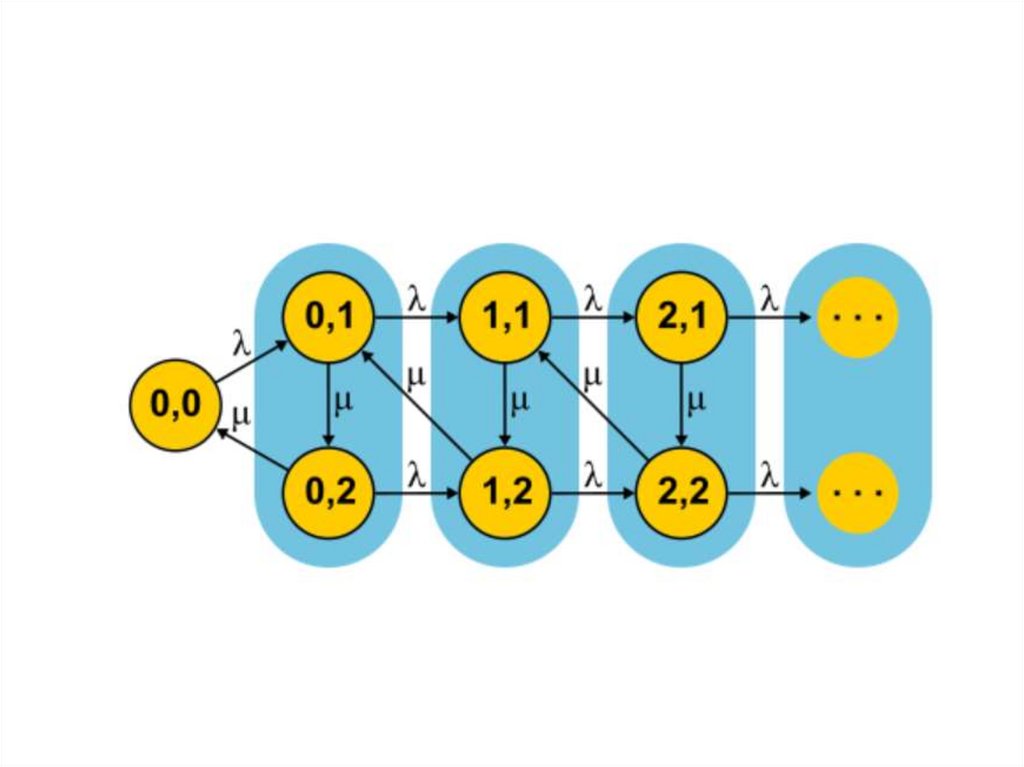
2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0)4. Размеченный граф переходов случайного процесса
5. Матрица интенсивностей переходов.
6. Система уравнений.
51
52.
2. МНОГОКАНАЛЬНАЯ СМО БЕЗ НАКОПИТЕЛЯ (M/M/N/0),
7. Расчет характеристик СМО.
1) нагрузка: y=λ/ =λb (по определению);
2) загрузка
3) коэффициент простоя системы:
4) среднее число заявок в системе
5) среднее число простаивающих приборов:
6) вероятность отказа в обслуживании
7) производительность системы
8) интенсивность потока не обслуженных заявок
9) среднее время пребывания заявок в системе
8. Анализ свойств системы.
52
53.
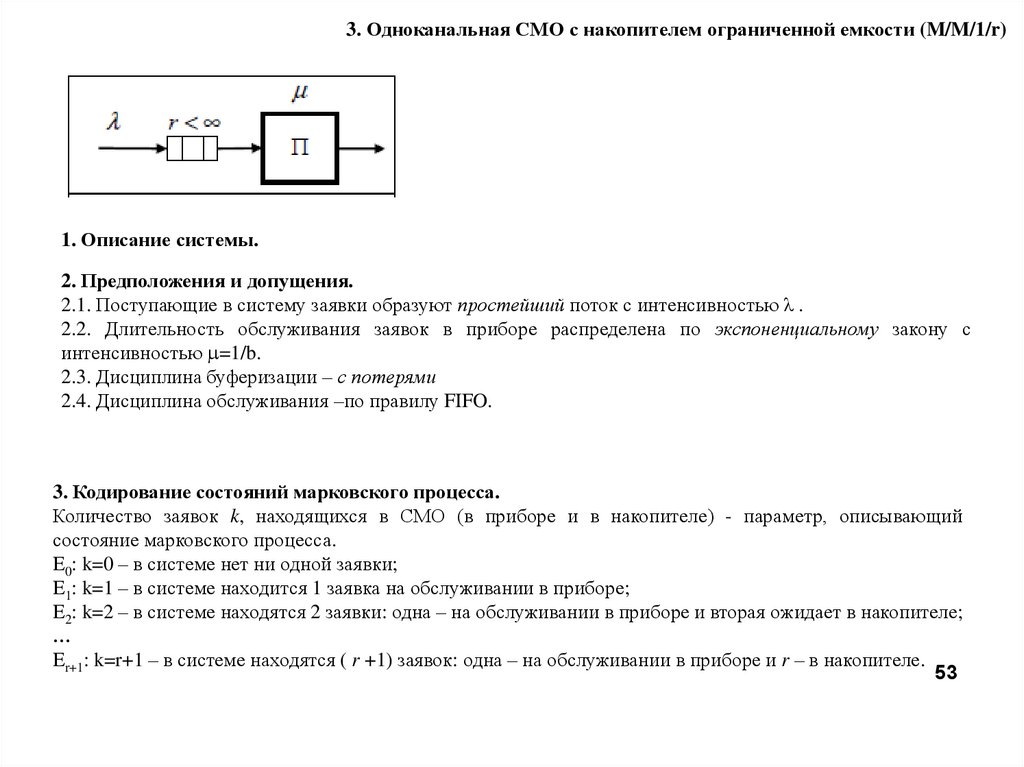
3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r)1. Описание системы.
2. Предположения и допущения.
2.1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ .
2.2. Длительность обслуживания заявок в приборе распределена по экспоненциальному закону с
интенсивностью =1/b.
2.3. Дисциплина буферизации – с потерями
2.4. Дисциплина обслуживания –по правилу FIFO.
3. Кодирование состояний марковского процесса.
Количество заявок k, находящихся в СМО (в приборе и в накопителе) - параметр, описывающий
состояние марковского процесса.
E0: k=0 – в системе нет ни одной заявки;
E1: k=1 – в системе находится 1 заявка на обслуживании в приборе;
E2: k=2 – в системе находятся 2 заявки: одна – на обслуживании в приборе и вторая ожидает в накопителе;
…
Er+1: k=r+1 – в системе находятся ( r +1) заявок: одна – на обслуживании в приборе и r – в накопителе.
53
54.
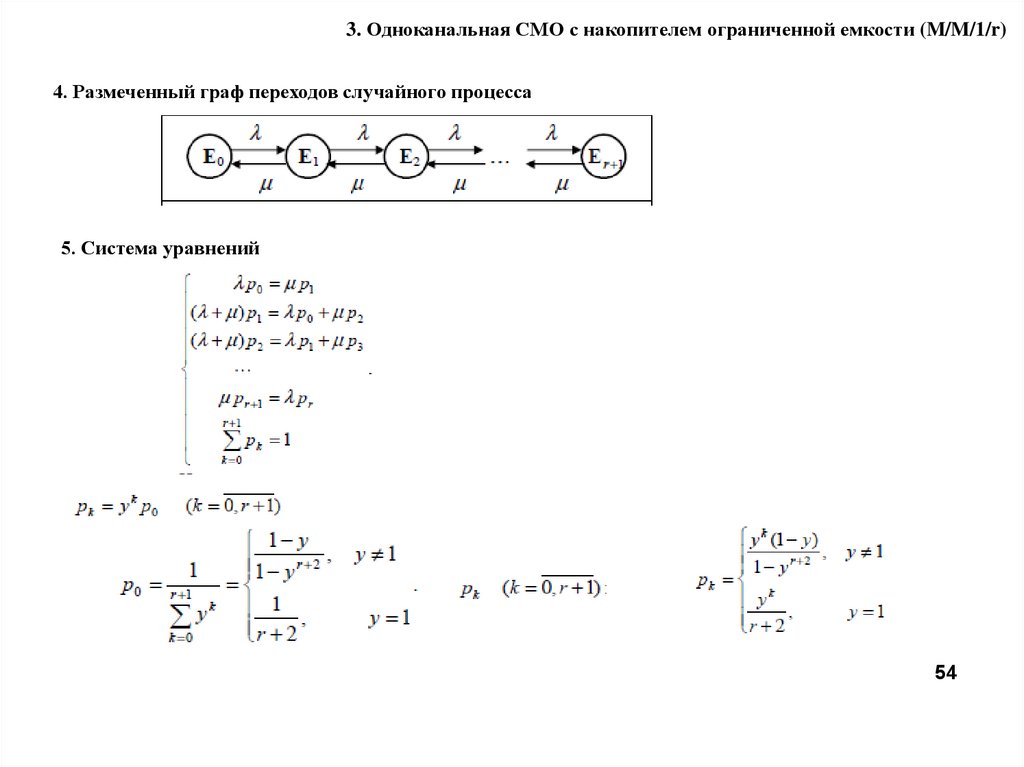
3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r)4. Размеченный граф переходов случайного процесса
5. Система уравнений
54
55.
3. Одноканальная СМО с накопителем ограниченной емкости (M/M/1/r)5. Расчет характеристик СМО.
.
1) нагрузка y=λ/ =λb;
2) загрузка
3) коэффициент простоя системы
4) среднее число заявок в очереди
5) среднее число заявок в системе
6) вероятность потери заявок
7) производительность системы (интенсивность потока обслуженных заявок)
8) интенсивность потока потерянных заявок
9) среднее время ожидания заявок
10) среднее время пребывания заявок
55
56.
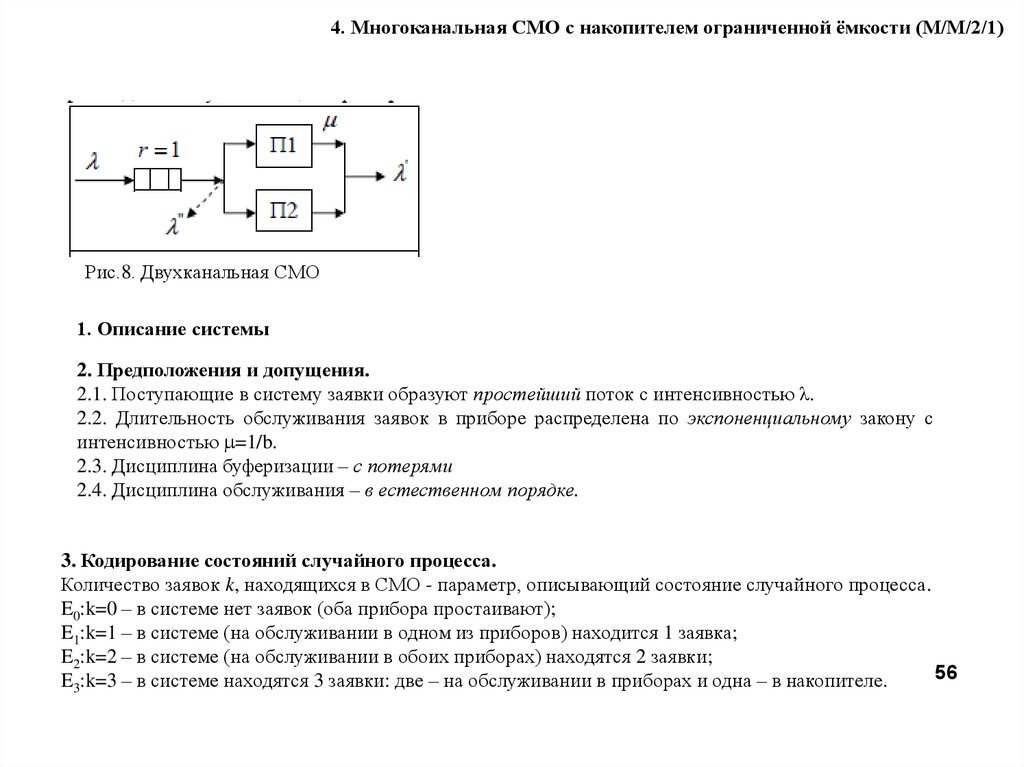
4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1)Рис.8. Двухканальная СМО
1. Описание системы
2. Предположения и допущения.
2.1. Поступающие в систему заявки образуют простейший поток с интенсивностью λ.
2.2. Длительность обслуживания заявок в приборе распределена по экспоненциальному закону с
интенсивностью =1/b.
2.3. Дисциплина буферизации – с потерями
2.4. Дисциплина обслуживания – в естественном порядке.
3. Кодирование состояний случайного процесса.
Количество заявок k, находящихся в СМО - параметр, описывающий состояние случайного процесса.
E0:k=0 – в системе нет заявок (оба прибора простаивают);
E1:k=1 – в системе (на обслуживании в одном из приборов) находится 1 заявка;
E2:k=2 – в системе (на обслуживании в обоих приборах) находятся 2 заявки;
56
E3:k=3 – в системе находятся 3 заявки: две – на обслуживании в приборах и одна – в накопителе.
57.
4. Многоканальная СМО с накопителем ограниченной ёмкости (M/M/2/1).
4. Размеченный граф переходов случайного процесса
5. Расчет характеристик СМО.
1) нагрузка: y=λ/ =λ/b
2) загрузка:
3) среднее число работающих приборов:
4) коэффициент простоя системы:
5) среднее число заявок в очереди:
6) среднее число заявок в системе:
7) вероятность потери заявок:
8) производительность системы (интенсивность потока обслуженных заявок):
9) интенсивность потока потерянных заявок:
10) среднее время ожидания заявок:
11) среднее время пребывания заявок:
57





















 mathematics
mathematics








