Анализ систем методами теории массового обслуживания

1.

Раздел 1.
Анализ систем методами теории
массового обслуживания
Тема 1.
Системы массового обслуживания
(СМО)

2.

Содержание лекции:
1. Основные понятия теории массового
обслуживания.
2. Классификация СМО, их основные элементы
и показатели.

3.

Вопрос 1.
Основные понятия
теории массового
обслуживания

4.

Системой массового обслуживания (СМО)
называется любая система, предназначенная для
обслуживания какого-либо потока заявок.
Примеры систем массового обслуживания:
посты технического обслуживания и ремонта
автомобилей;
билетные кассы;
справочные бюро;
магазины, поликлиники;
аудиторские фирмы;
телефонные станции и т. д.

5.

В CMО обслуживаемый объект называют заявкой
(требованием).
В общем случае под заявкой обычно понимают
запрос на удовлетворение некоторой потребности,
например, разговор с абонентом, посадка самолета,
покупка билета, ремонт (обслуживание) автомобиля,
получение материалов на складе, отдых в отпуске и т.п.
Средства, обслуживающие требования, называются
обслуживающими
устройствами
(каналами
обслуживания).
Например, это каналы телефонной связи, посадочные
полосы,
мастера-ремонтники,
билетные
кассиры,
погрузочно-разгрузочные точки на базах и складах, отели,
перевозчики и пр.

6.

Предметом
теории
массового
обслуживания
является
установление
зависимости
между
факторами,
определяющими
функциональные
возможности
СМО,
и
эффективностью
ее
функционирования.
Основной задачей теории СМО является изучение
режима функционирования обслуживающей системы
и исследование явлений, возникающих в процессе
обслуживания.
Пример. Одной из критических характеристик
обслуживающей системы является время пребывания
требования в очереди.
Как можно его сократить?

7.

Одним из вариантов является увеличение
количества обслуживающих устройств.
Однако каждое дополнительное устройство требует
определенных материальных затрат.
Т.О.,
в
теории
СМО
возникают
задача
оптимизации:
каким образом достичь определенного уровня
обслуживания (максимального сокращения очереди
или
потерь
требований,
не
дождавшихся
обслуживания) при минимальных затратах, связанных
как с самим процессом обслуживания, так и с
простоем обслуживающих устройств при отсутствии
требований.

8.

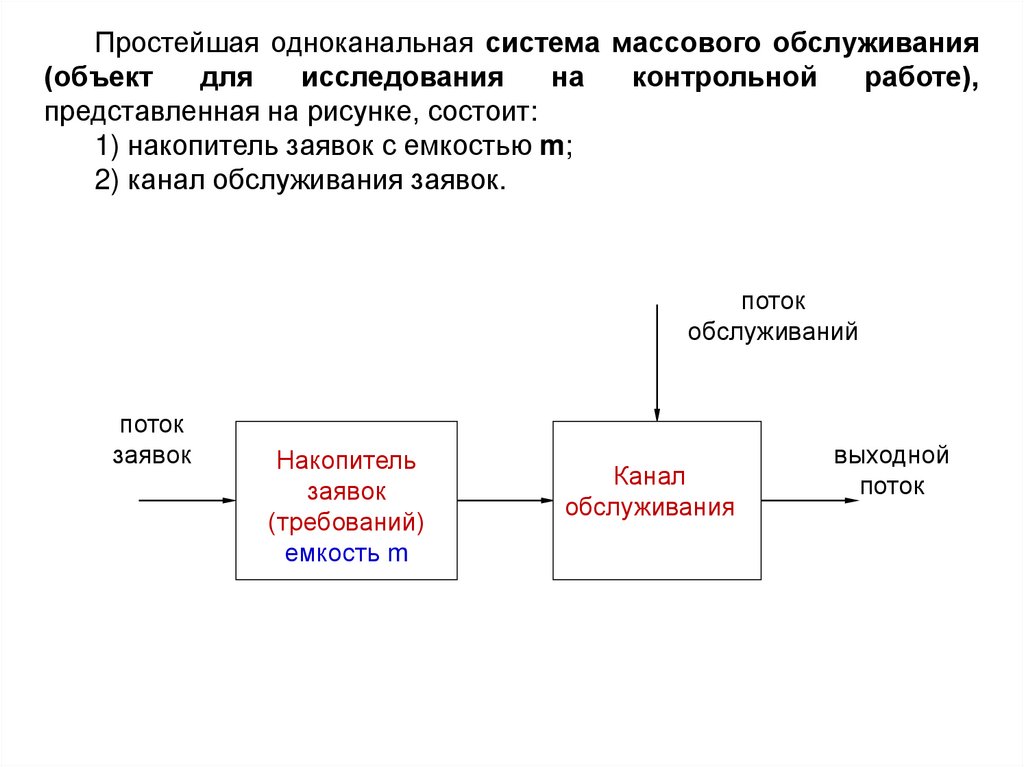
Простейшая одноканальная система массового обслуживания
(объект
для
исследования
на
контрольной
работе),
представленная на рисунке, состоит:
1) накопитель заявок с емкостью m;
2) канал обслуживания заявок.
поток
обслуживаний
V
U
(t)
поток
заявок
Накопитель
(запоминающее
Накопитель
устройство)
заявок
(требований)
емкость m
(t)
Канал
обслуживания
Канал
(процессор)
обслуживания
выходной
поток

9.

Вопрос 2.
Классификация СМО и
их основные элементы

10.

В
большинстве
случаев
все
параметры,
описывающие
СМО,
являются
случайными
величинами или случайными функциями, поэтому
эти системы относятся к классу стохастических
систем.
Случайный характер потока заявок (требований),
а также длительности обслуживания приводит к
тому, что в СМО происходит случайный процесс.
По характеру случайного процесса, происходящего
в СМО, различают системы:
марковские;
немарковские.

11.

Случайный процесс называется марковским, если
для любого момента времени t вероятностные
характеристики процесса в будущем зависят только от
его состояния в данный момент t и не зависят от того,
когда и как система пришла в это состояние.
Переходы системы из состояния в состояние
происходят под действием каких-то потоков событий
(поток заявок, поток отказов).
В
случае
немарковских
процессов
задачи
исследования СМО значительно усложняются и требуют
применения статистического моделирования, численных
методов с использованием ЭВМ.

12.

Андрей Андреевич Марков
2.06.1856 – 20.07.1922
Андрей Андреевич Марков русский математик, академик,
внёсший большой вклад в
теорию вероятностей, математический анализ и теорию
чисел.
А.
А.
Марков
является
первооткрывателем обширного
класса
стохастических
процессов с дискретной и
непрерывной
временно́й
компонентой, названных его
именем.
Теория
цепей
Маркова выросла в важную
область
научных
исследований - теорию марковских
случайных процессов,.

13.

По составу СМО бывают одноканальные (с одним
обслуживающим устройством) и многоканальными (с
большим числом обслуживающих устройств).
Многоканальные системы могут состоять из
обслуживающих устройств как одинаковой, так и разной
производительности.
По времени пребывания заявок в очереди до начала
обслуживания системы делятся на три группы:
• с ожиданием,
• с отказами,
• смешанного типа.
В СМО с ожиданием очередная заявка, застав все
устройства занятыми, становится в очередь и ожидает
обслуживания до тех пор, пока одно из устройств не
освободится.
Это – наиболее распространенные системы.

14.

СМО с ожиданием можно разбить на 2 большие
группы: замкнутые и разомкнутые.
К замкнутым относятся системы, в которых
поступающий поток заявок ограничен.
Например, мастер, задачей которого является
наладка станков в цехе, должен периодически их
обслуживать. Каждый налаженный станок становится в
будущем потенциальным источником требований на
наладку. В подобных системах общее число
циркулирующих заявок конечно и чаще всего
постоянно.
Если имеется бесконечное число заявок, то
системы называются разомкнутыми.
Примерами подобных систем могут служить
магазины, кассы вокзалов, портов и др.
Для этих систем поступающий поток требований
можно считать неограниченным.

15.

В системах с отказами поступившая заявка,
застав все обслуживающие устройства занятыми,
покидает систему.
Примером системы с отказами может служить
работа автоматической телефонной станции.
В системах смешанного типа поступившая
заявка, застав все устройства занятыми, становятся в
очередь и ожидают обслуживания в течение
ограниченного времени.
Не дождавшись обслуживания в установленное
время, например, до конца рабочего дня, заявка
покидает систему.
Такие
системы
еще
называют
СМО
с
ограниченным ожиданием.

16.

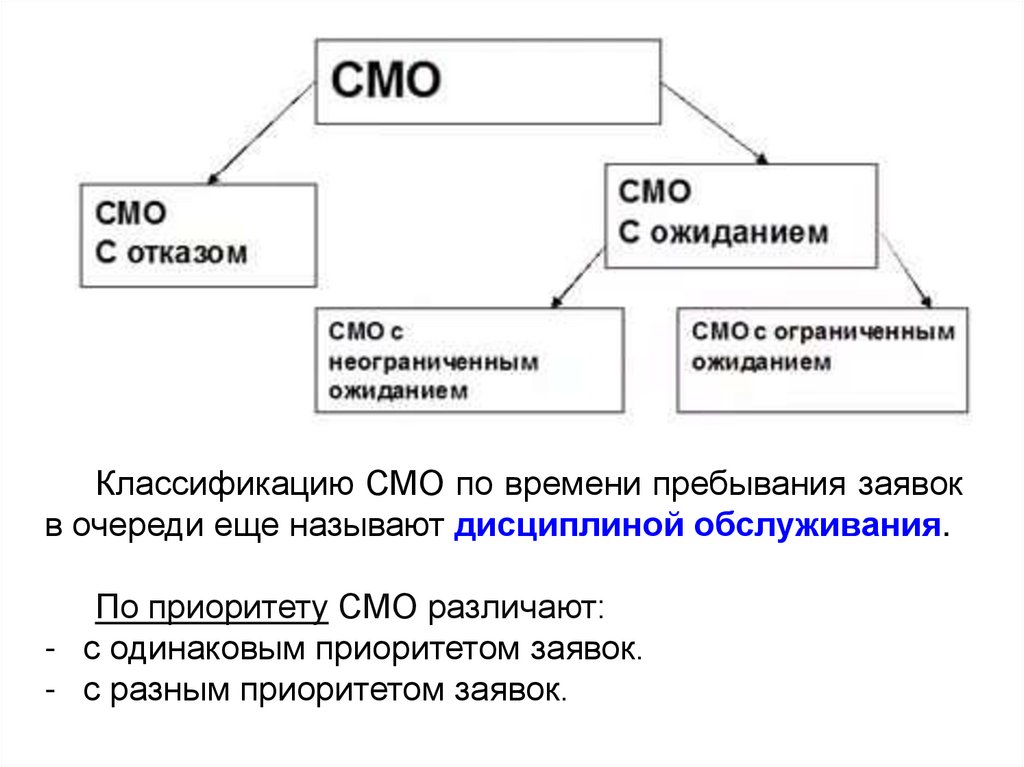
Классификацию СМО по времени пребывания заявок
в очереди еще называют дисциплиной обслуживания.
По приоритету СМО различают:
- с одинаковым приоритетом заявок.
- с разным приоритетом заявок.

17.

Т.О., основными элементами СМО являются:
входящий поток заявок;
очередь заявок;
каналы (устройства) обслуживания;
выходящий поток заявок.
Входящий поток заявок представляет собой
совокупность заявок, которые поступают в систему и
нуждаются в обслуживании.
Входящий поток заявок изучается с целью
установления закономерностей этого потока и
дальнейшего улучшения качества обслуживания.
В
большинстве
случаев
входящий
поток
неуправляем и зависит от ряда случайных факторов.
Число заявок, поступающих в единицу времени,
является случайной величиной.

18.

Случайной величиной является также интервал
времени между соседними поступающими заявками.
Однако среднее количество заявок, поступивших в
единицу времени, и средний интервал времени между
соседними поступающими заявками предполагаются
заданными.
Среднее число заявок, поступающих в систему
обслуживания за единицу времени, называется
интенсивностью
поступления
заявок,
и
определяется следующим соотношением:
1
.

19.

Для многих реальных процессов поток заявок
достаточно
хорошо
описывается
законом
распределения Пуассона.
( t )
t
Pm (t )
e .
m!
m
Данная
формула
поступления
на
определяет
обслуживание
вероятность
m
заявок
за
промежуток времени t.
e – основание натурального логарифма (2,7183…).
Такой
поток
(пуассоновским).
называется
простейшим

20.

Если количество испытаний n достаточно
велико,
а
вероятность
p
появления
события А в отдельно взятом испытании
весьма мала (p ≤ 0,05-0,1), то вероятность
того, что в данной серии испытаний
событие А появится ровно m раз, можно
приближенно
вычислить
по
формуле
Пуассона, где λ = n*p.

21.

Семион Пуассон - французский
математик, физик, механик
(21.06.1781 – 25.04.1840)
Работа
Семиона
Дени
Пуассона «Исследования о вероятности
приговоров в уголовных и гражданских
делах», в которой было введено данное
распределение, была опубликована в 1837 году.
Примеры других ситуаций, которые можно смоделировать,
применив это распределение:
1) поломки оборудования, длительность исполнения ремонтных
работ стабильно работающим сотрудником,
2) ошибка печати,
3) рост колонии бактерий,
4) дефекты в длинной ленте или цепи,
5) импульсы счётчика радиоактивного излучения,
6) количество забиваемых футбольной командой голов и др.

22.

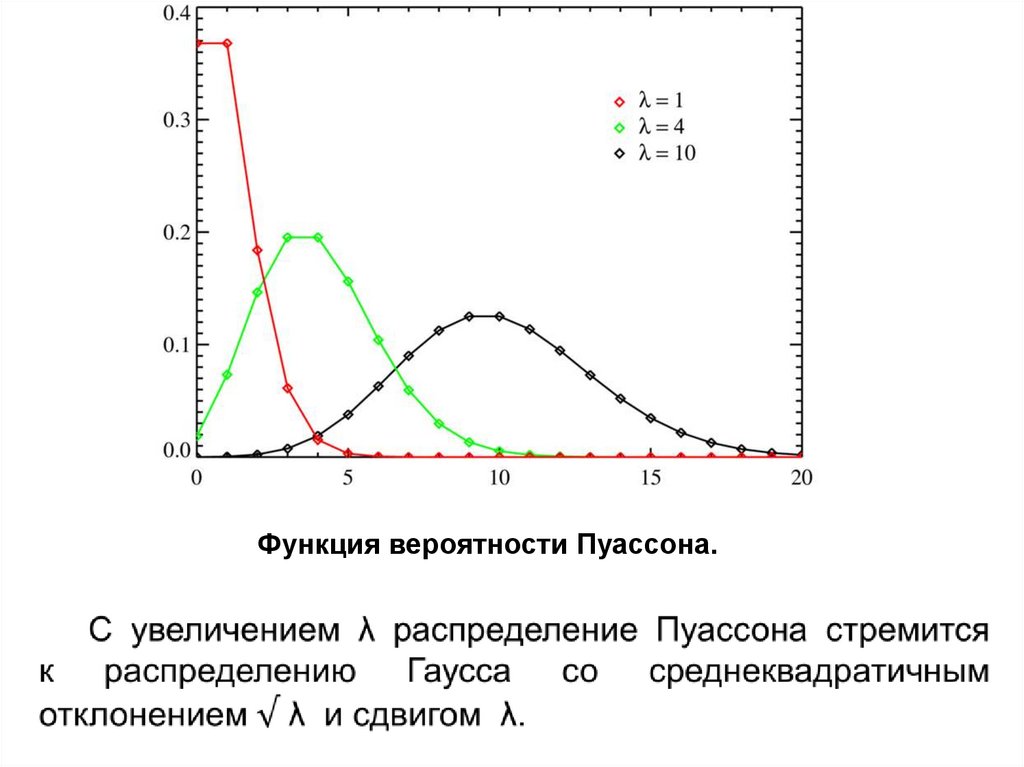
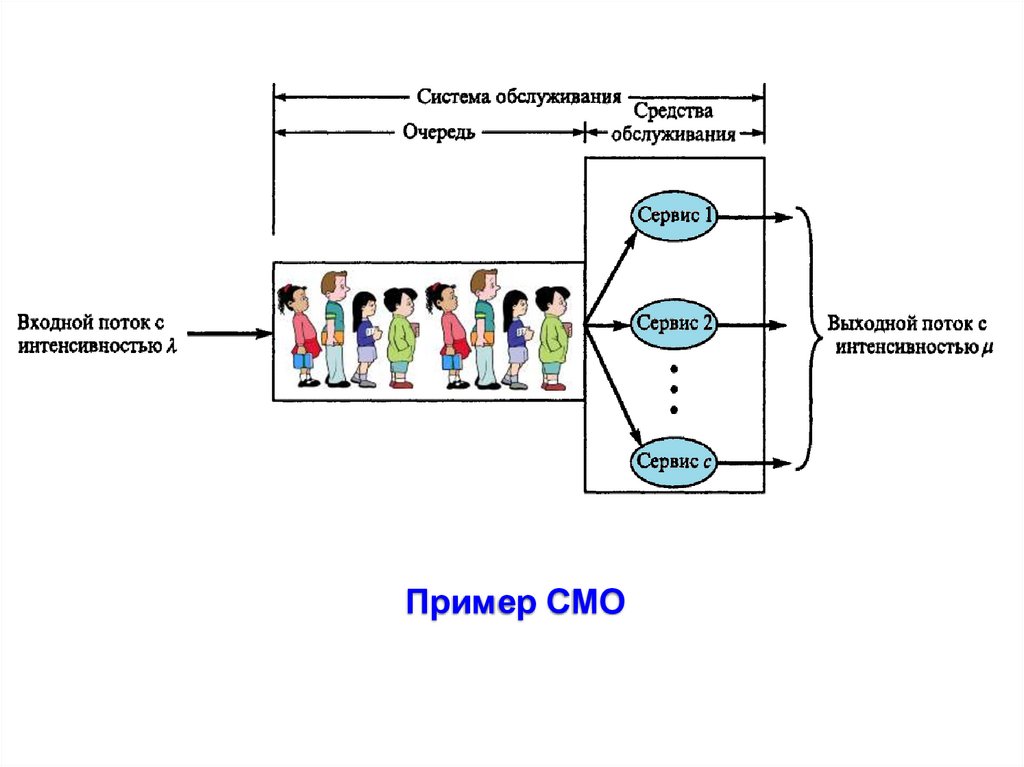
Функция вероятности Пуассона.

23. Пример СМО

24.

Простейший поток характеризуется
важными свойствами:
стационарностью;
отсутствием последействия;
ординарностью.
тремя
1. Стационарность выражает неизменность
вероятностного режима потока по времени.
Это значит, что число заявок, поступающих в
систему в равные промежутки времени, в среднем
должно быть постоянным, т.е.
λ = const
Например, число вагонов, поступающих под
погрузку в среднем в сутки должно быть одинаковым
для различных периодов времени.

25.

Для краткой характеристики СМО Д. Кендалл
ввел символику (нотацию):
A/B/m/n/k
где:
А – характеристика входного потока;
В – характеристика потока обслуживания;
m - число обслуживающих каналов;
n – количество мест ожидания (емкость
накопителя).
k – количество источников.
A
и
B
описываются
функциями
распределения интервалов между заявками во
входном потоке и распределения времен
обслуживания.

26.

2. Отсутствие последействия обуславливает
взаимную независимость поступления того или иного
числа заявок на обслуживание в непересекающиеся
промежутки времени.
Это значит, что число заявок, поступающих в
данный отрезок времени, не зависит от числа заявок,
обслуженных в предыдущем промежутке времени.
Например, число автомобилей, прибывших за
материалами в десятый день месяца, не зависит от
числа автомобилей, обслуженных в четвертый или
любой другой день данного месяца.

27.

3. Свойство ординарности выражает практическую
невозможность одновременного поступления двух или
более заявок.
На практике условия простейшего потока не всегда
строго
выполняются.
Часто
имеет
место
нестационарность процесса (например, в различные
часы дня и различные дни месяца поток заявок меняется,
он может быть интенсивнее утром или в последние дни
месяца).
Существует также наличие последействия, когда
количество заявок на отпуск товаров в конце месяца
зависит от их удовлетворения в начале месяца.
Наблюдается и явление неоднородности, когда
несколько клиентов одновременно пребывают на склад за
материалами.
Однако в целом пуассоновский закон распределения
с высоким приближением отражает многие процессы
массового обслуживания.

28.

Почему такое предположение в ряде важных случаев
оказывается верным, дает ответ общая теорема
А.Я.Хинчина, которая представляет исключительную
теоретическую и практическую ценность.
Эта теорема имеет место в случае, когда входящий
поток можно представить в виде суммы большого числа
независимых потоков, меньших по интенсивности с
суммарным потоком.
Формулировка теоремы А.Я.Хинчина:
«Если входящий поток представляет собой сумму
большого
числа
независимых
между
собой
стационарных и ординарных потоков, каждый из
которых вносит малый вклад в общую сумму, то при
одном дополнительном условии аналитического
характера (которое обычно выполняется на практике)
поток близок к простейшему».

29.

Александр Яковлевич Хи́нчин
(7.07.1894 – 18.11.1959)
советский математик,
профессор МГУ, доктор физикоматематических наук.
Является одним из создателей советской школы
теории вероятностей (им получены важные результаты
в области предельных теорем, открыт закон повторного
логарифма, дано определение случайного стационарного
процесса и заложены основы теории таких процессов).
Методы и результаты теории вероятностей Хинчин
широко использовал в качестве математического аппарата
статистической физики, им разработаны математические
методы теории массового обслуживания.

30. Основные показатели СМО:

Время между соседними заявками распределено по
показательному закону:
f (t ) e t .
Время
обслуживания заявок также подчиняется
показательному закону:
t
f (t ) e
,
где μ – интенсивность потока обслуживания (среднее число
заявок, обслуживаемых в единицу времени).
Отношение
интенсивности входящего потока к
интенсивности потока обслуживания называется
загрузкой системы – среднее число заявок,
приходящих за среднее время обслуживания одной
заявки.
.