Построение графика квадратичной функции

1.

Построение графика
квадратичной функции

2.

1 способ - выделение квадрата двучлена
Построить график функции
у = x2 +2x –1
2
2
у =x +2x–1 =(x + 2x+1)–1–1 =
= (х + 1)2 – 2
2
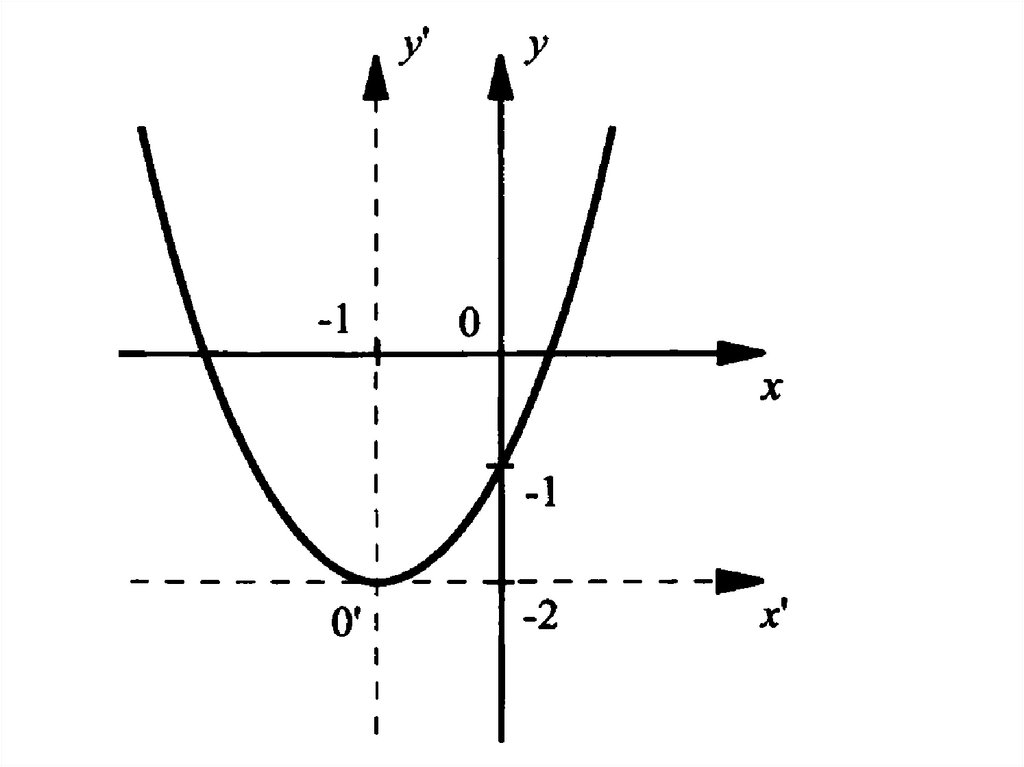
у =(х + 1) – 2

3.

Значит, график функции у = x2 +2x –1 можно
построит с помощью двух параллельных
переносов – сдвига вдоль оси ох на 1 единичный
отрезок влево и сдвига вдоль оси оу на 2
единичных отрезка вниз
Построим вспомогательные прямые:
x=m=-1, у=n=-2.
Они пересекутся в точке с координатой (-1; -2) –
это вершина параболы
Т.к. а >0, ветви параболы направлены вверх
Строим в новой системе координат график
функции у = x2

4.

5.

;
2 способ-алгоритм построения графика квадратичной
функции
1. Найти координаты вершины параболы (x0; y0) по формулам
x0=-b:2a. Вычислить y0 .
2. Отметить ее на координатной плоскости.
3. Провести через вершину параболы вспомогательные оси.
Ось x0- ось симметрии параболы.
4. Определить направление ветвей параболы (для а > 0 ветви
параболы направлены вверх, для а < 0 – вниз).
5. Найти точки пересечения параболы с осью абсцисс. Для этого
определить нули функции у(х), решив квадратное уравнение
у(х) = 0. Отметить эти точки на оси абсцисс.
6. Построить несколько точек, принадлежащих одной из ветвей
параболы (справа или слева от ее вершины).
7. Построить симметрично точки, принадлежащие другой ветви
параболы.
8. Соединить отмеченные точки плавной линией.

6.

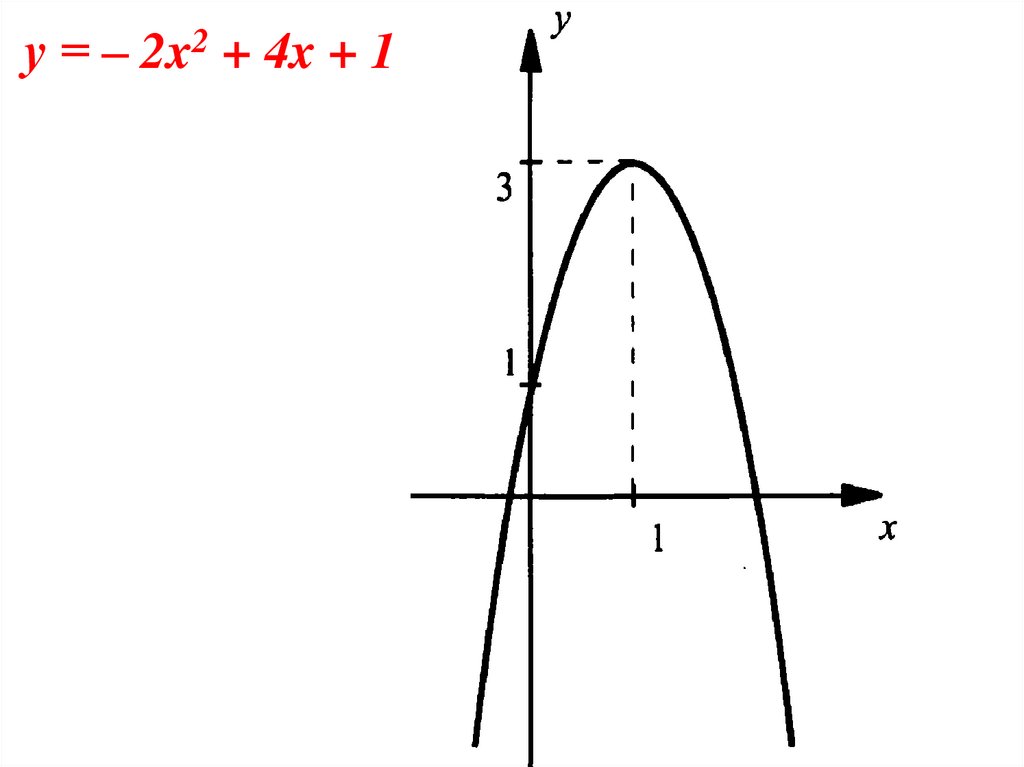
Построить график функции у = – 2x2 + 4x + 1
В.п.(1; 3)
х=1 – ось симметрии
а= -2, ветви параболы направлены вниз.
Нули функции: – 2x2 + 4x + 1=0
Дополнительные точки
х=0 у=1
х= -1 у= -5

7.

у = – 2x2 + 4x + 1

8.

Дополнительные задания
№ 1-доп
Постройте графики данных функций и найдите
координаты точек пересечения получившихся
парабол с осями координат:
а) y = x2 – 4x;
б) y = 2x2 – 2;
в) y = x2 – 2x – 3.
№ 2-доп
Зная координаты вершины параболы задайте
квадратичную функцию х0 = 2, у0 = -4