Геометрия. 9 класс

1.

ГЕОМЕТР
ИЯ
9 КЛАСС

2.

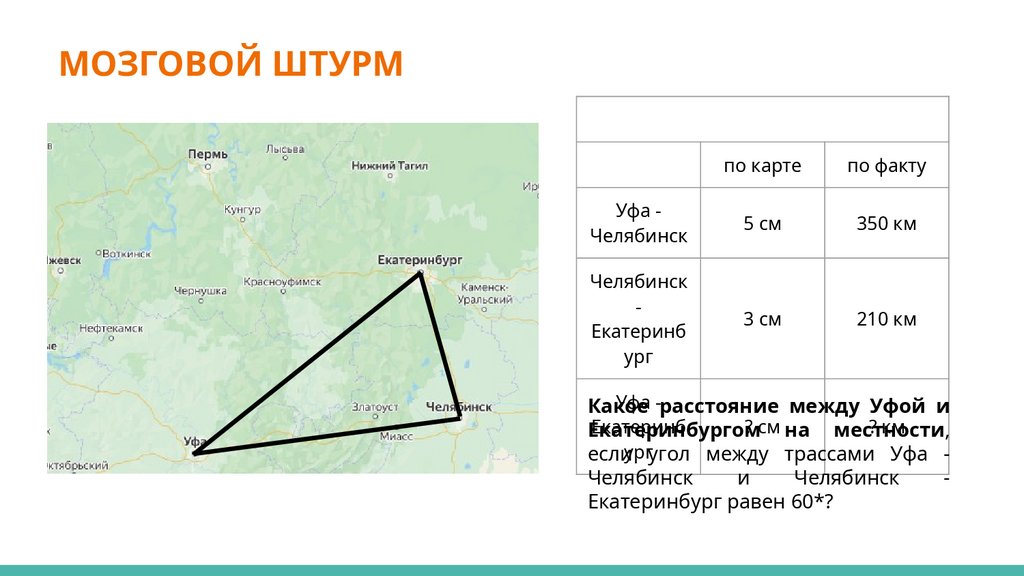
МОЗГОВОЙ ШТУРМ
по карте
по факту
Уфа Челябинск
5 см
350 км
Челябинск
Екатеринб
ург
3 см
210 км
Уфа -расстояние между Уфой и
Какое
Екатеринб
? см на местности,
? км
Екатеринбургом
еслиургугол между трассами Уфа Челябинск
и
Челябинск
Екатеринбург равен 60*?

3.

МОЗГОВОЙ ШТУРМ
1
2
3 см
3
5 см
H
Найдите фактическое расстояние между Уфой и
Екатеринбургом (в км), если масштаб карты 1 :
7000000. Результат округлите до целого числа.
4
5
Каким образом можно
решить задачу?
Что следует сделать в
первую очередь?
На что следует обратить
внимание? Почему? Что
можно применить и найти?
Какую длину отрезка можно
вычислить?
Каким образом это сделать?
Что еще можно определить?
Можно ли теперь сказать,
что ответ на вопрос задачи
получен? Какие знания были
применены чтобы получить
ответ на вопрос задачи?
Существует ли, на ваш
взгляд, более быстрый и
рациональный способ
решения данной задачи?

4.

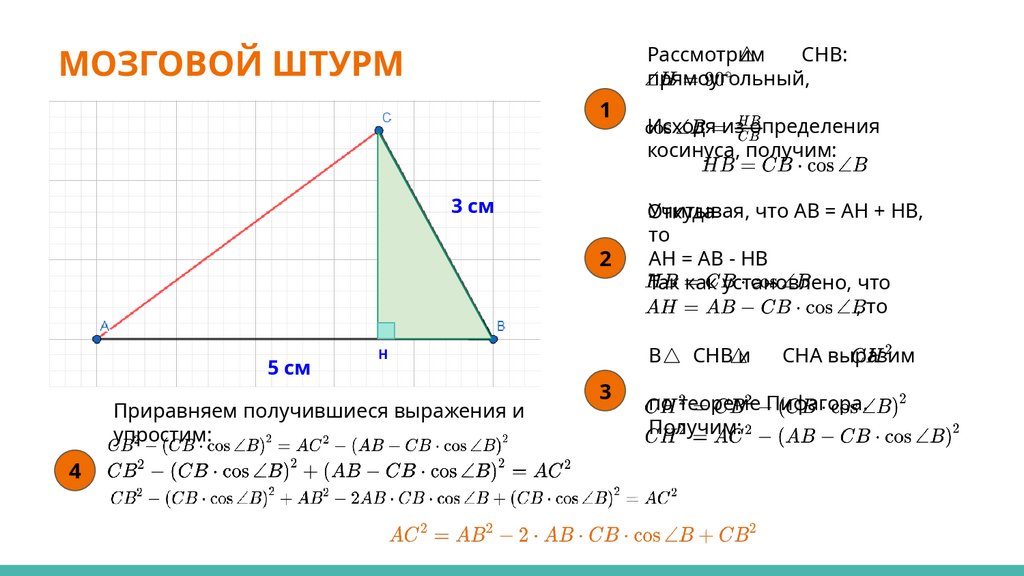
МОЗГОВОЙ ШТУРМ
Рассмотрим
CHB:
прямоугольный,
1
3 см
2
5 см
4
Учитывая, что AB = AH + HB,
Откуда
то
AH = AB - HB
Так как установлено, что
, то
В
H
Приравняем получившиеся выражения и
упростим:
Исходя из определения
косинуса, получим:
3
CHB и
CHA выразим
по теореме Пифагора.
Получим:

5.

МОЗГОВОЙ ШТУРМ
3 см
5 см
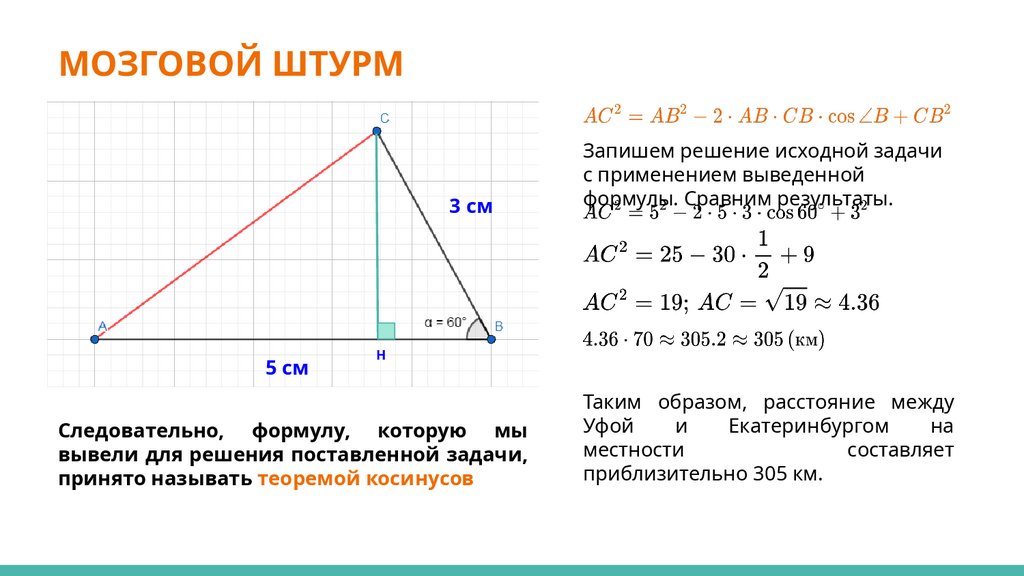
Запишем решение исходной задачи
с применением выведенной
формулы. Сравним результаты.
H
Следовательно, формулу, которую мы
вывели для решения поставленной задачи,
принято называть теоремой косинусов
Таким образом, расстояние между
Уфой
и
Екатеринбургом
на
местности
составляет
приблизительно 305 км.

6.

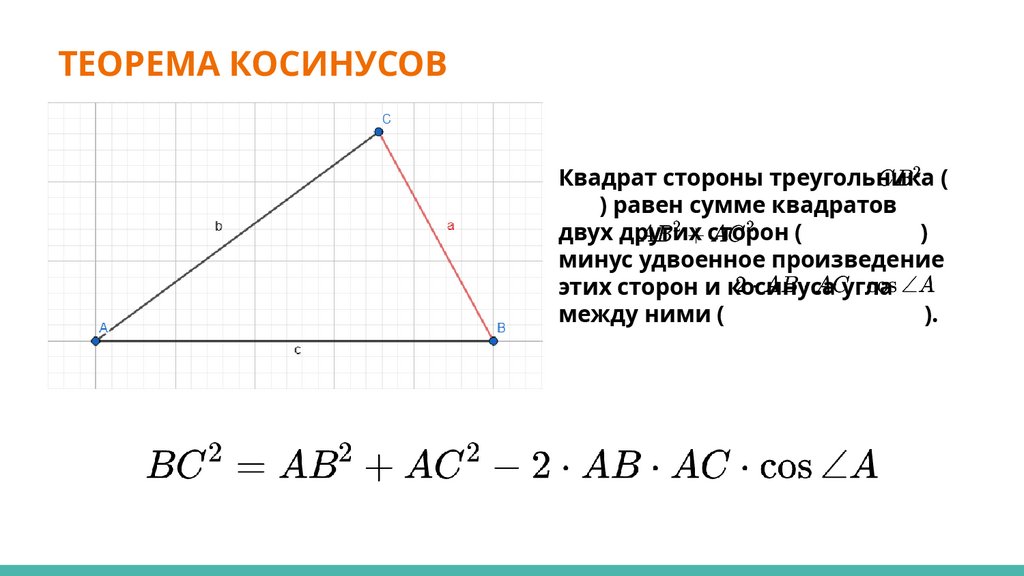
ТЕОРЕМА КОСИНУСОВ
Квадрат стороны треугольника (
) равен сумме квадратов
двух других сторон (
)
минус удвоенное произведение
этих сторон и косинуса угла
между ними (
).

7.

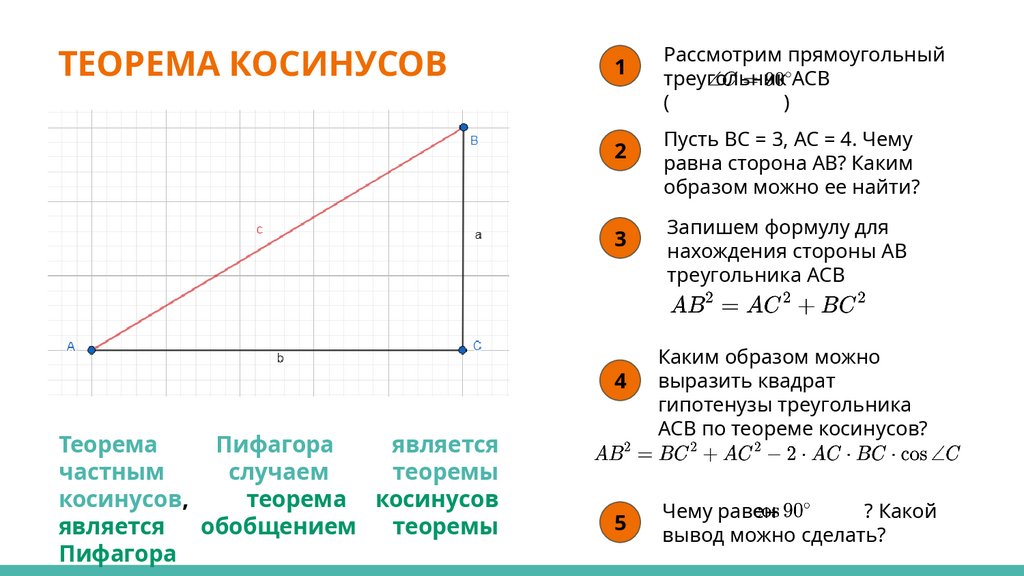
ТЕОРЕМА КОСИНУСОВ
1
2
3
4
Теорема
Пифагора
является
частным
случаем
теоремы
косинусов,
теорема косинусов
является
обобщением
теоремы
Пифагора
5
Рассмотрим прямоугольный
треугольник ACB
(
)
Пусть BC = 3, AC = 4. Чему
равна сторона АВ? Каким
образом можно ее найти?
Запишем формулу для
нахождения стороны АВ
треугольника АСВ
Каким образом можно
выразить квадрат
гипотенузы треугольника
АСВ по теореме косинусов?
Чему равен
? Какой
вывод можно сделать?

8.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Найдите сторону МК
треугольника MNK, если NK = 5,
MN =
,
Решение:
1) Так как угол N - угол между
сторонами NK и MN треугольника
MNK, то для решения поставленной
задачи применим теорему
косинусов, а именно:
1
2) Определим значение
.
Так
3) Подставим данные в формулу и
вычислим МК:
Ответ: МК =
Найдите основание
равнобедренного треугольника,
если боковая сторона - 4, а угол при
вершине Решение:
1) Пусть a - основание
равнобедренного треугольника, тогда
b - боковые стороны данного
треугольника.
По теореме косинусов:
2
2) Определим значение
.
3) Подставим данные в формулу и
вычислим основание:
Ответ: a =

9.

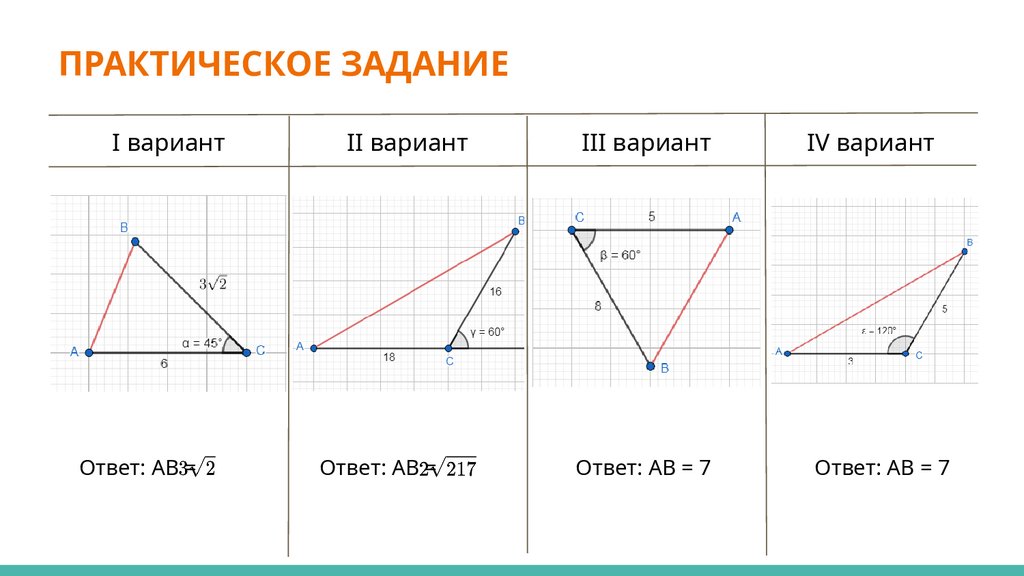
ПРАКТИЧЕСКОЕ ЗАДАНИЕ
I вариант
Ответ: АВ =
II вариант
Ответ: АВ =
III вариант
IV вариант
Ответ: АВ = 7
Ответ: АВ = 7

10.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Найти косинус меньшего угла треугольника, если АВ = 9, ВС
= 10, АС = 15
Решение:
1)
Учитывая,
что
в
треугольнике
напротив
меньшей
стороны
лежит
меньший угол, придем к
выводу, что необходимо найти
косинус угла С.
2) Согласно теореме косинусов:
3) Подставим данные значения
в формулу:
4) Упростим получившееся выражение:
5) Вычислим значение косинуса угла С:
Ответ:

11.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ
I вариант
II вариант
III вариант
Найдите
косинус
большего
по
величине
угла
треугольника,
стороны
которого
равны 5, 8 и 11
Найдите
косинус
среднего
по
величине
угла
треугольника,
стороны
которого
равны 6, 9 и 11
Найдите
косинус
меньшего
по
величине
угла
треугольника,
стороны
которого
равны 4, 7 и 10
Найдите
косинус
большего
по
величине
угла
треугольника,
стороны
которого
равны 4, 8 и
Ответ: 0.95
Ответ: -0.5
Ответ: -0.4
Ответ:
IV вариант

12.

ВИДЫ ТРЕУГОЛЬНИКОВ
Пусть a, b, c - стороны треугольника, причем a - его наибольшая сторона.
Треугольник
остроугольный, если
Треугольник
тупоугольный, если
Треугольник
прямоугольный, если

13.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ
I вариант
II вариант
III вариант
IV вариант
Установите
остроугольным,
прямоугольным или
тупоугольным
является
треугольник,
стороны
которого
равны 14, 10, 16
Установите
остроугольным,
прямоугольным или
тупоугольным
является
треугольник,
стороны
которого
равны 7, 24, 25
Установите
остроугольным,
прямоугольным или
тупоугольным
является
треугольник,
стороны
которого
равны 10, 8, 14
Установите
остроугольным,
прямоугольным или
тупоугольным
является
треугольник,
стороны
которого
равны 30, 40, 51
Ответ:
остроугольный
Ответ:
прямоугольный
Ответ:
тупоугольный
Ответ:
тупоугольный

14.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ
В треугольнике больший угол при
основании равен
, а высота делит
основание на отрезки, равные 20 и 21.
а) Найдите большую боковую сторону.
б) Установите остроугольным,
тупоугольным или прямоугольным
является данный треугольник. Ответ
обоснуйте.
Дано:
в) Решите задачу двумя
способами.
Найти:
а) большую
боковую сторону;
б) установить вид
треугольника.
Решение:
1)
Рассмотрим
_______.
Так
как
________________ (по условию) и __________,
то _________________________________
____________________________________________
_______________.
2) По условию задачи __________ и
Значит,
__________,
следовательно,
____________________________________________
__________________________________________.
______.
3)
По
теореме
косинусов
________________________________.
____________________________________________
________________
Зная
стороны треугольника, а именно,
____________________________________________
что
______________, ___________, __________,
_______________.
определим вид
.
Так как _______ - наибольшая сторона, то
________________
____________________________________________
_______________.
Получим
____________________________________________

15.

РЕШЕНИЕ ЗАДАЧ
1
Решите задачу на готовом чертеже,
где ABCD - параллелограмм
Рассмотрим
Решите задачу на готовом чертеже,
где ABCD - параллелограмм
Решение:
Решение:
АВСD параллелограмм
(по условию),
значит,
АВСD параллелограмм
(по условию),
значит,
. Применим
теорему
косинусов
Найдем значение диагонали
параллелограмма ABCD.
Таким образом,
2
.
. Ответ:
Рассмотрим
. Так как
т
о
Рассмотрим
.<B =
Применим теорему
поиска АС. косинусов
для
Ответ:

16.

ТЕОРЕМА КОСИНУСОВ В
ЖИЗНИ
В
небольших
домах
(особенно
с
неэксплуатируемой
мансардой)
для
устройства одно- и двускатной крыши
можно применить более дешевую и легкую
конструкцию - решетчатые стропила.
Данная конструкция нашла широкое
применение при строительстве домов и
мостовой архитектуре. Была изобретена
и запатентована Альбертом Финком немецким инженером - строителем в
1854 году.
Используя данные чертежа,
найдите длину балки АВ (по теореме
косинусов)

17.

ДОПОЛНИТЕЛЬНЫЙ
МАТЕРИАЛ
Ссылка на урок
в РЭШ
Онлайн тест