Случайная изменчивость (примеры)

1.

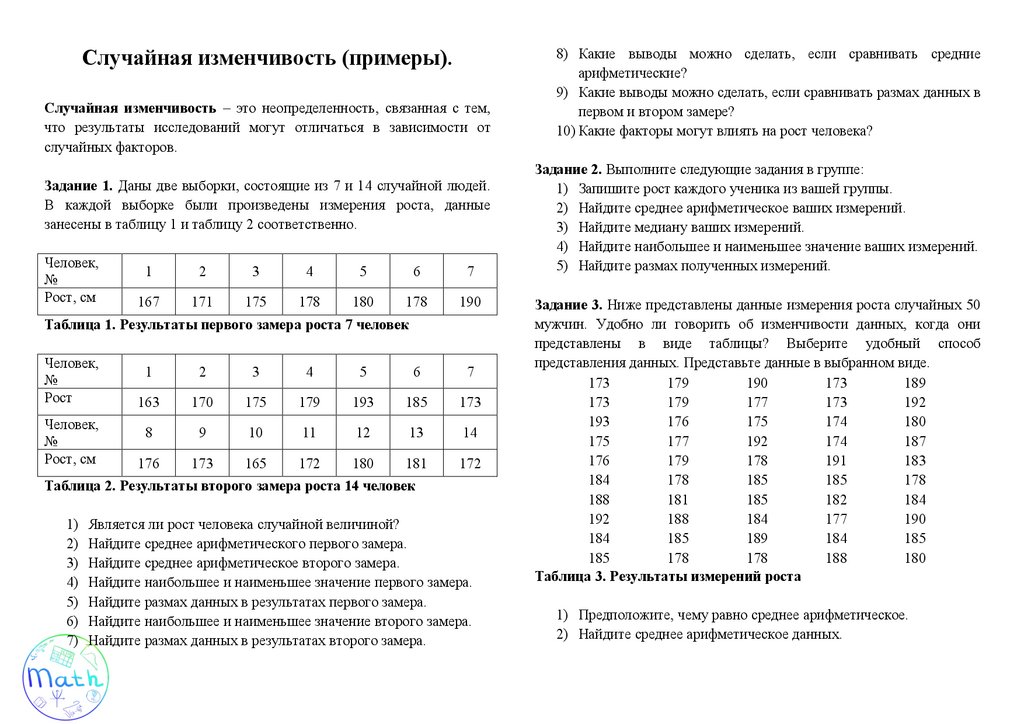
Случайная изменчивость (примеры).
Случайная изменчивость – это неопределенность, связанная с тем,
что результаты исследований могут отличаться в зависимости от
случайных факторов.
Задание 1. Даны две выборки, состоящие из 7 и 14 случайной людей.
В каждой выборке были произведены измерения роста, данные
занесены в таблицу 1 и таблицу 2 соответственно.
Человек,
№
Рост, см
1
2
3
4
5
6
7
167
171
175
178
180
178
190
Таблица 1. Результаты первого замера роста 7 человек
Человек,
№
Рост
Человек,
№
Рост, см
1
2
3
4
5
6
7
163
170
175
179
193
185
173
8
9
10
11
12
13
14
176
173
165
172
180
181
172
Таблица 2. Результаты второго замера роста 14 человек
1) Является ли рост человека случайной величиной?
2) Найдите среднее арифметического первого замера.
3) Найдите среднее арифметическое второго замера.
4) Найдите наибольшее и наименьшее значение первого замера.
5) Найдите размах данных в результатах первого замера.
6) Найдите наибольшее и наименьшее значение второго замера.
7) Найдите размах данных в результатах второго замера.
8) Какие выводы можно сделать, если сравнивать средние
арифметические?
9) Какие выводы можно сделать, если сравнивать размах данных в
первом и втором замере?
10) Какие факторы могут влиять на рост человека?
Задание 2. Выполните следующие задания в группе:
1) Запишите рост каждого ученика из вашей группы.
2) Найдите среднее арифметическое ваших измерений.
3) Найдите медиану ваших измерений.
4) Найдите наибольшее и наименьшее значение ваших измерений.
5) Найдите размах полученных измерений.
Задание 3. Ниже представлены данные измерения роста случайных 50
мужчин. Удобно ли говорить об изменчивости данных, когда они
представлены в виде таблицы? Выберите удобный способ
представления данных. Представьте данные в выбранном виде.
173
179
190
173
189
173
179
177
173
192
193
176
175
174
180
175
177
192
174
187
176
179
178
191
183
184
178
185
185
178
188
181
185
182
184
192
188
184
177
190
184
185
189
184
185
185
178
178
188
180
Таблица 3. Результаты измерений роста
1) Предположите, чему равно среднее арифметическое.
2) Найдите среднее арифметическое данных.

2.

3) Почему среднее арифметическое сильно отличается от среднего
арифметического полученного в задание 1?
Задание 4. В таблице представлена температура днём в ноябре 2023
года в городе Санкт-Петербург.
День
1
2
3
4
5
6
7
8
9
10
Температура,
11
4
4
5
6
6
8
7
7
7
С°
Таблица 4. Среднесуточная температура в Санкт-Петербурге в
ноябре 2023 года.
1) Изменчива ли температура днём в Санкт-Петербурге?
2) Является ли изменчивость среднесуточной температуры
случайной?
3) Какие факторы могут влиять на это?
Задание 5. Друзья решили узнать, как номинальная масса шоколадки
отличается от реальной массы. В таблице представлены результаты
замеров массы 10 купленных шоколадок. Номинальная масса 200
грамм.
Шоколадка,
1
2
3
4
5
6
7
8
9
10
№
Вес, гр
202 203 201 198 200 197 200 201 196 202
Таблица 5. Результаты 10 измерений массы шоколадки
1) Определите среднее арифметическое для полученных данных.
2) Найдите наибольшее и наименьшее значение.
3) Найдите размах данных
4) Сколько
полученных
измерений
равны
среднему
арифметическому? А больше? А меньше?
5) Какие выводы мы можем сделать?
Для каждого товара существует допустимое отклонение, в
зависимости от качества стандарта производства, это называется
допустимой погрешностью. Погрешность обозначается с помощью
знака «±».
Погрешность может быть абсолютная, то есть величина,
выраженная в единицах измерения, и относительная погрешность,
величина, выраженная в процентах.
Если изменение массы изделия превышает допустимую
погрешность, то оно считается бракованным.
Задание 6. При покупке мешка риса был указан вес: 5 кг ± 0,05 кг.
Выберите варианты с массой риса, которые находятся в рамках
допустимой погрешности.
1) 4950 г
2) 5,1 кг
3) 4050 г
4) 5,03 кг
Задание 7. У Дмитрий в машине сломался спидометр, у него
получилось определить, что его спидометр показывает на 6 км/ч
меньше, чем есть на самом деле. Штраф приходит если скоростной
режим был превышен на 20 км/ч от разрешенного на данном участке.
Определите в каких случаях Дмитрию придет штраф?
Скорость на спидометре
Разрешенная скорость
1
104
90
2
25
20
3
128
110
Таблица 6. Скорость Дмитрия на различных участках

3.

Задание 8. Рассмотрим с вами производство шин для машин.
Номинальный вес, установленный компанией, равен 8,2 кг.
Допустимая погрешность согласно стандарту качества производства
составляет ±0,05 кг. На производстве произвели замеры 20 случайно
выбранных шин. Результаты замеров представлены в таблице 7.
Шина,
1
2
3
4
5
6
7
8
9
10
№
Вес,
8,0 8,23 8,22 8,21 8,27 8,16 8,2 8,18 8,22 8,16
кг
Шина,
11
12
13
14
15
16
17
18
19
20
№
Вес,
8,15 8,23 8,2 8,21 8,19 8,16 8,25 8,21 8,17 8,19
кг
Таблица 7. Результаты замера 20 случайно выбранных шин
1) Найдите среднее арифметическое.
2) Определите рамки допустимого веса с учетом погрешности.
Входит ли в них среднее арифметическое? Можем ли мы
сделать вывод, что все шины проходят по стандарту качества?
Почему?
3) Какие номера шин будут считаться бракованными?
4) Какой процент шин удовлетворяет стандарту качества?
Задание 9. В таблице 8 представлены данные урожайности зерновых
культур в регионе P за последние 20 лет. На упаковке с семенами было
указано, что масса, полученных семян, составляет 350 ц ± 7%. Все 20
лет высаживались одни и те же семена.
Год,
1
2
3
4
5
6
7
8
№
Масса,
367 356 349 355 350 320 378 382
ц
Год,
11
12
13
14
15
16
17
18
№
Масса,
328 357 334 381 300 367 332 378
ц
Таблица 8. Урожайность зерновых культур в городе P.
9
10
348
332
19
20
351
341
1) Какой может быть номинальная масса семян, которые взойдут?
2) Найдите среднее значение урожайности зерновых культур.
Можно ли на основе данных о среднем значении сказать, что во
все года всхожесть семян была в рамках допустимых
погрешностей?
3) В какие года реальная масса урожайности зерновых культура
была не в рамках допустимых погрешностей? Чем это можно
объяснить?
4) Какой процент лет урожайность семян удовлетворяла
погрешностям?