Многогранники и тела вращения

1.

Многогранники и тела
вращения
Понарьина Евгения Валентиновна
МБОУ СОШ №43
2016 год
г.Воронеж

2.

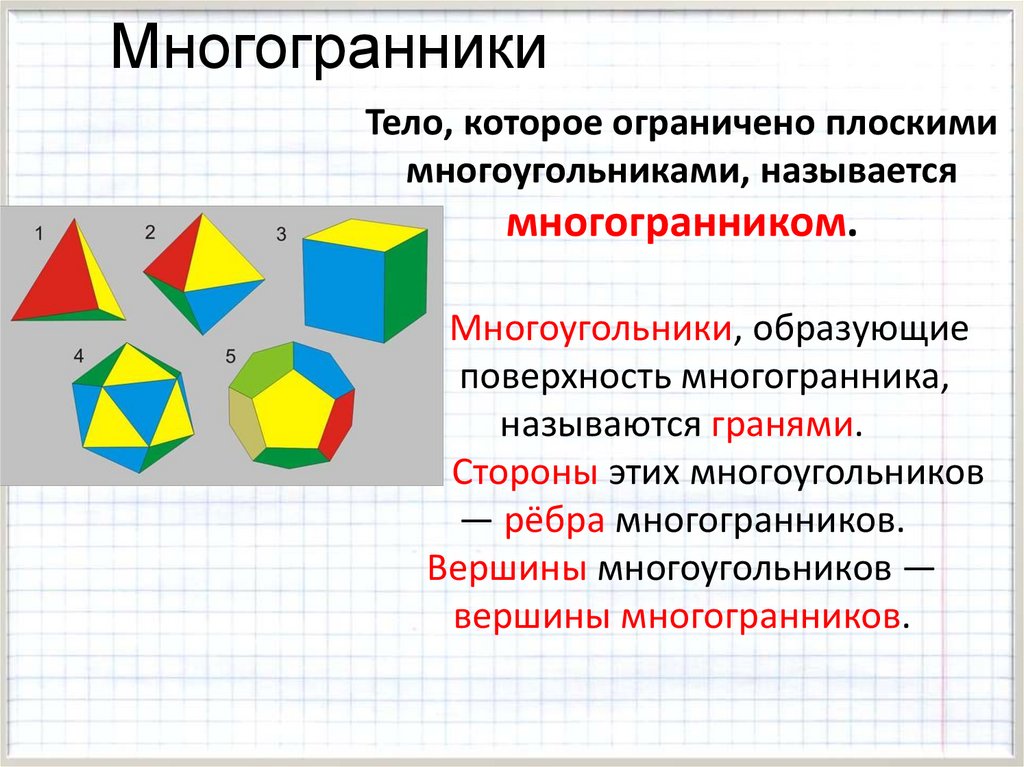
Многогранники
Тело, которое ограничено плоскими
многоугольниками, называется
многогранником.
Многоугольники, образующие
поверхность многогранника,
называются гранями.
Стороны этих многоугольников
— рёбра многогранников.
Вершины многоугольников —
вершины многогранников.

3.

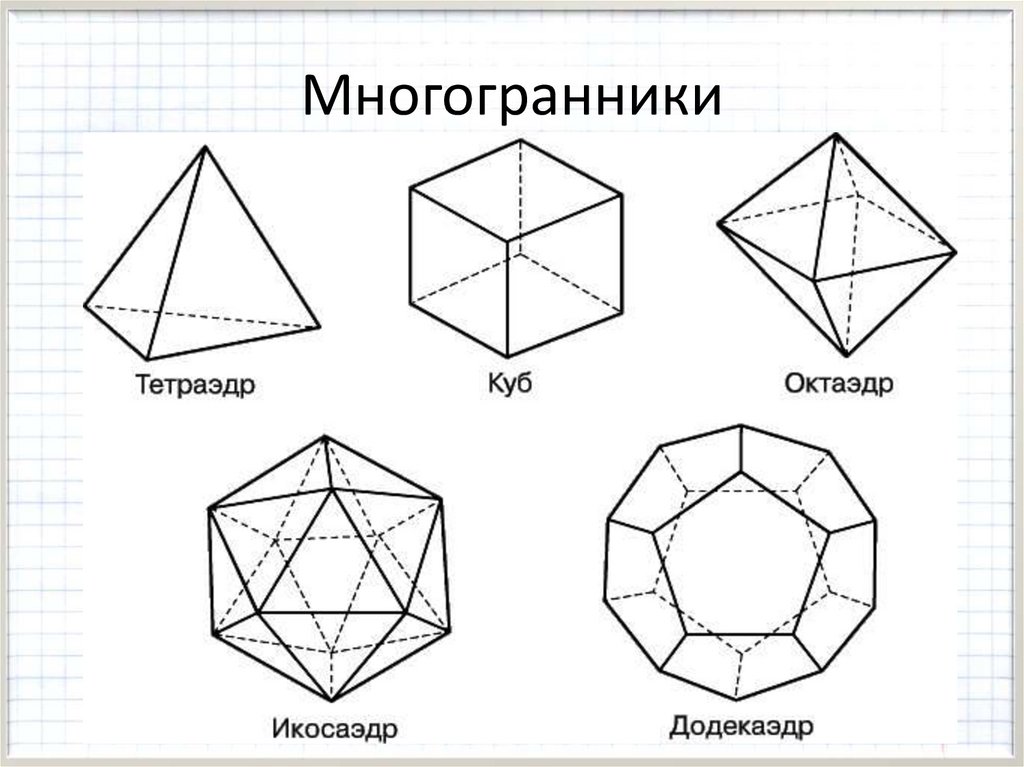
Многогранники

4.

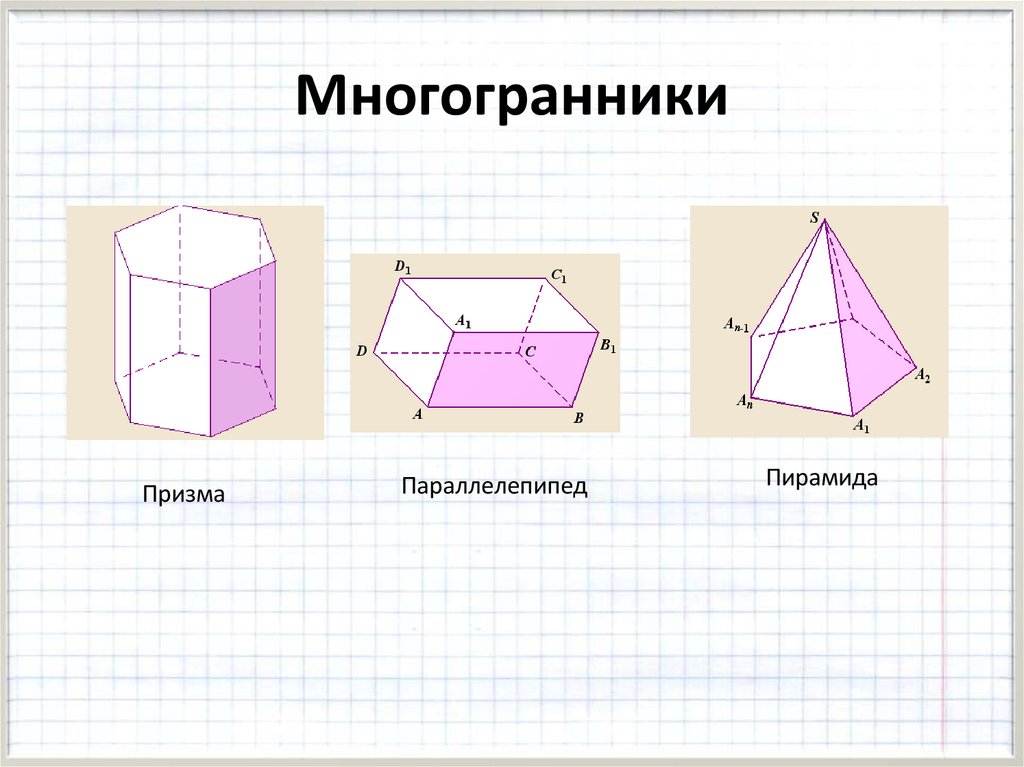
Многогранники
Призма
Параллелепипед
Пирамида

5.

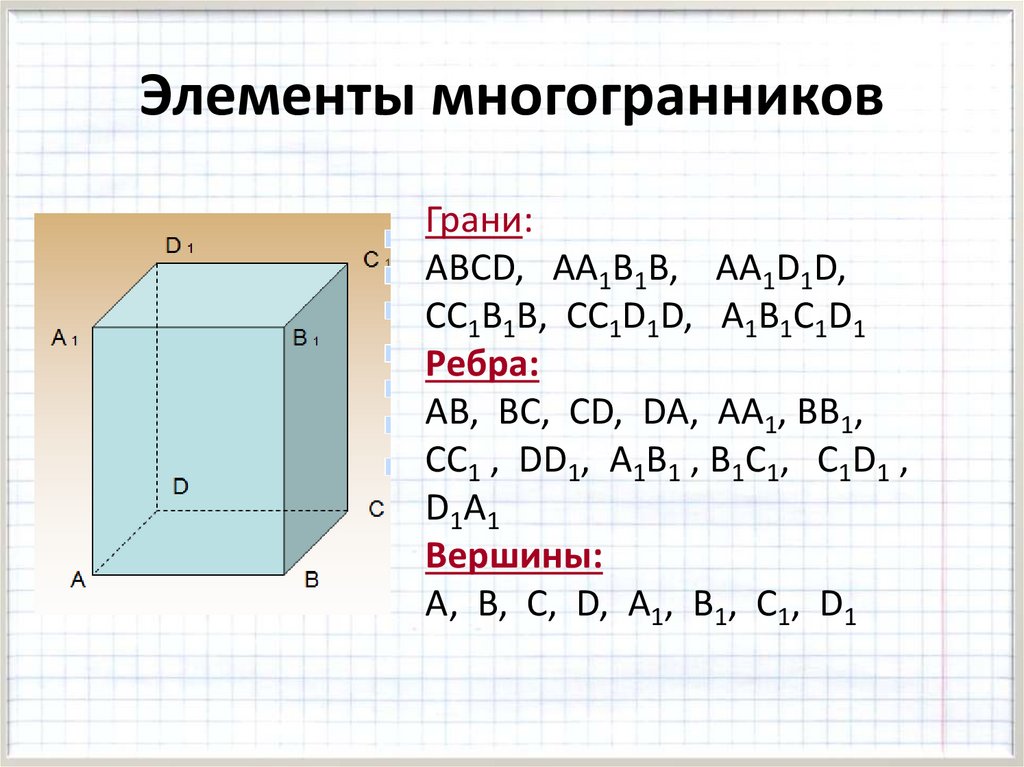
Элементы многогранников
Грани:
АBСD, АА1В1В, АА1D1D,
СС1В1В, СС1D1D, А1В1С1D1
Ребра:
АB, ВС, СD, DA, АА1, ВВ1,
СС1 , DD1, А1В1 , В1С1, С1D1 ,
D1A1
Вершины:
А, B, С, D, А1, В1, С1, D1

6.

Призма
Опр: Призмой называется многогранник, состоящий из
двух равных многоугольников, расположенных в
параллельных плоскостях и n параллелограммов.
Многоугольники – основания призмы
Параллелограммы – грани призмы
Параллельные отрезки, соединяющие вершины
многоугольников – боковые ребра призмы

7.

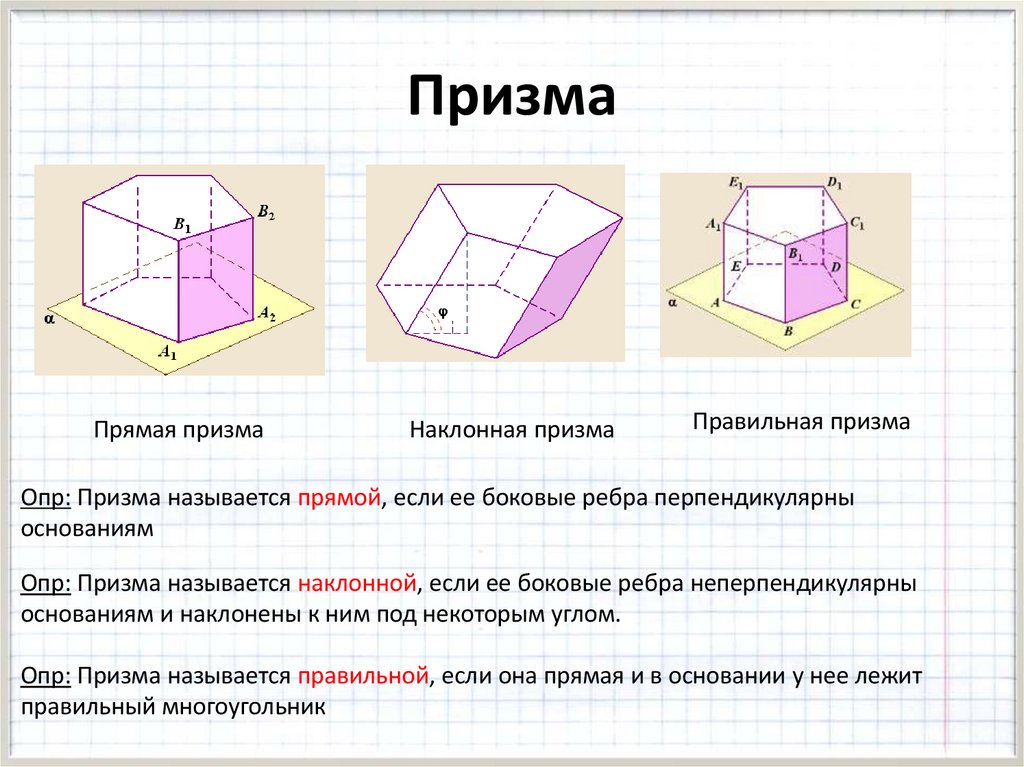
Призма
Прямая призма
Наклонная призма
Правильная призма
Опр: Призма называется прямой, если ее боковые ребра перпендикулярны
основаниям
Опр: Призма называется наклонной, если ее боковые ребра неперпендикулярны
основаниям и наклонены к ним под некоторым углом.
Опр: Призма называется правильной, если она прямая и в основании у нее лежит
правильный многоугольник

8.

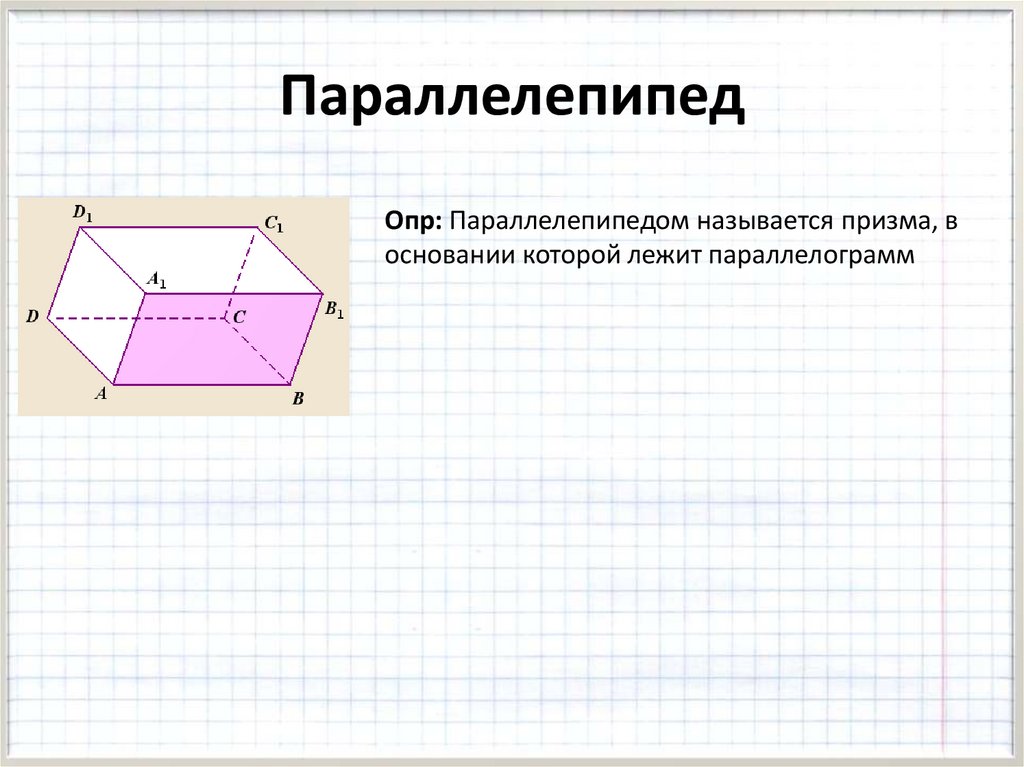
Параллелепипед
Опр: Параллелепипедом называется призма, в
основании которой лежит параллелограмм

9.

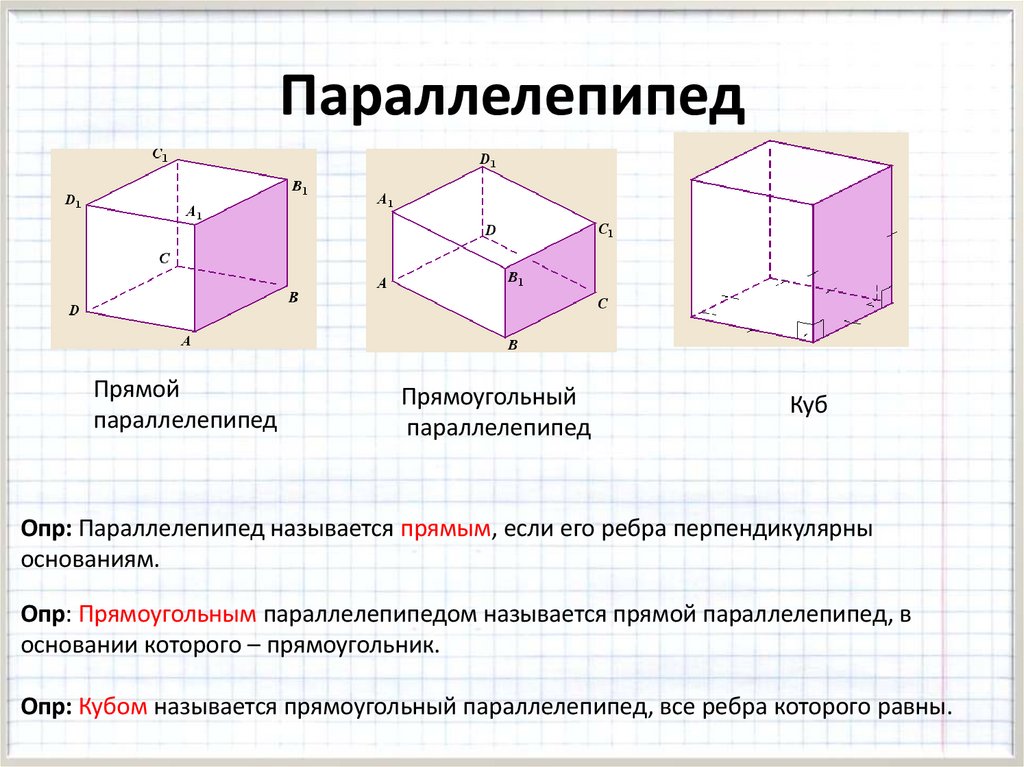
Параллелепипед
Прямой
параллелепипед
Прямоугольный
параллелепипед
Куб
Опр: Параллелепипед называется прямым, если его ребра перпендикулярны
основаниям.
Опр: Прямоугольным параллелепипедом называется прямой параллелепипед, в
основании которого – прямоугольник.
Опр: Кубом называется прямоугольный параллелепипед, все ребра которого равны.

10.

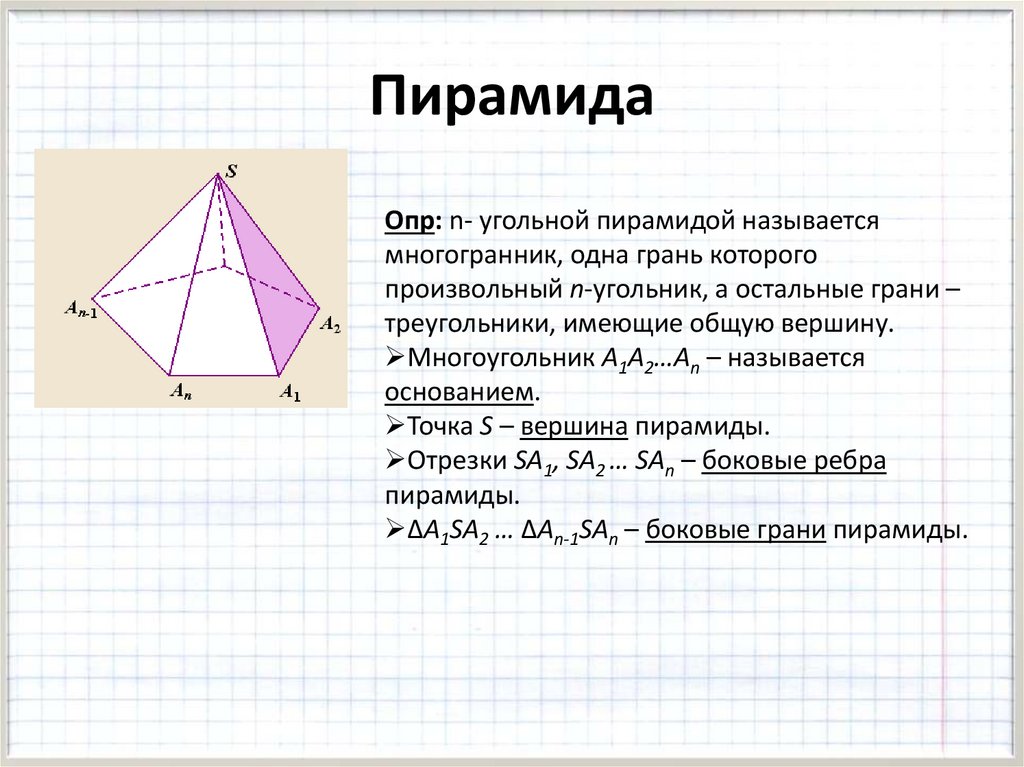
Пирамида
Опр: n- угольной пирамидой называется
многогранник, одна грань которого
произвольный n-угольник, а остальные грани –
треугольники, имеющие общую вершину.
Многоугольник А1А2…Аn – называется
основанием.
Точка S – вершина пирамиды.
Отрезки SA1, SA2 … SAn – боковые ребра
пирамиды.
ΔA1SA2 … ΔAn-1SAn – боковые грани пирамиды.

11.

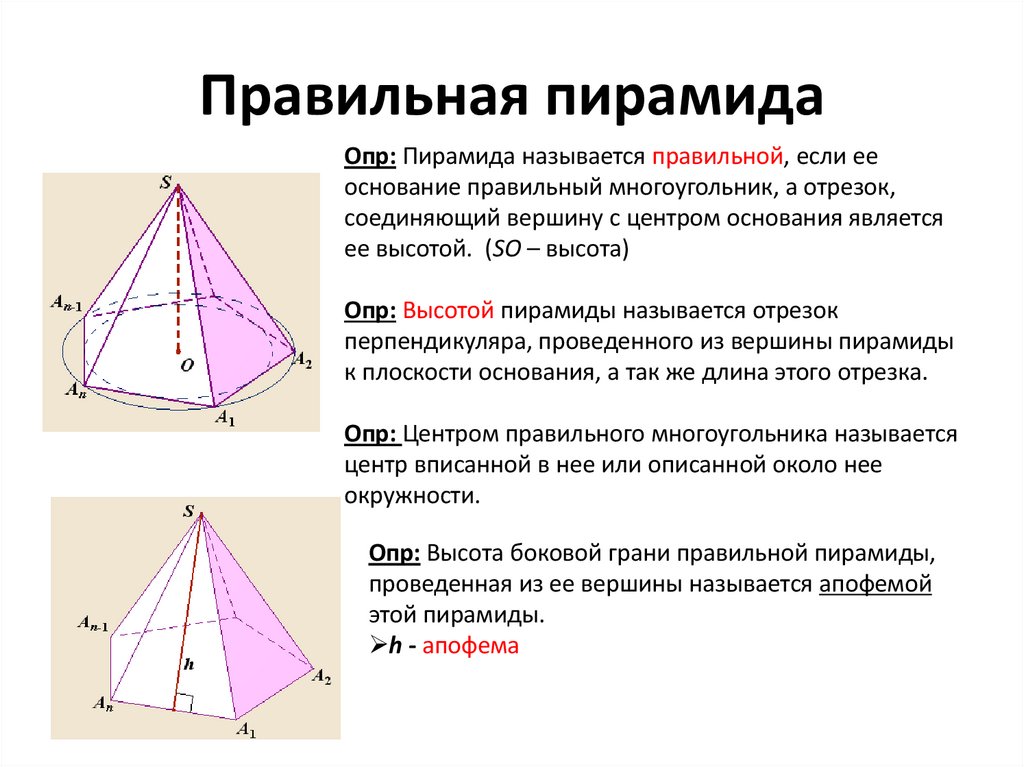
Правильная пирамида
Опр: Пирамида называется правильной, если ее
основание правильный многоугольник, а отрезок,
соединяющий вершину с центром основания является
ее высотой. (SO – высота)
Опр: Высотой пирамиды называется отрезок
перпендикуляра, проведенного из вершины пирамиды
к плоскости основания, а так же длина этого отрезка.
Опр: Центром правильного многоугольника называется
центр вписанной в нее или описанной около нее
окружности.
Опр: Высота боковой грани правильной пирамиды,
проведенная из ее вершины называется апофемой
этой пирамиды.
h - апофема

12.

13.

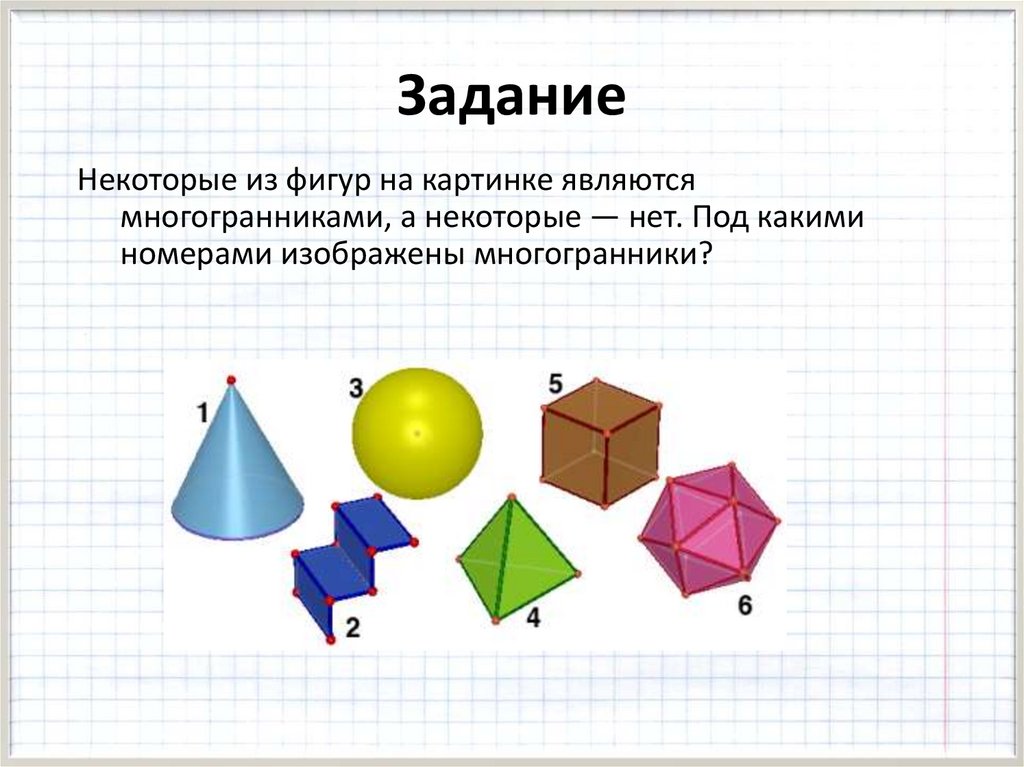
Задание
Некоторые из фигур на картинке являются
многогранниками, а некоторые — нет. Под какими
номерами изображены многогранники?

14.

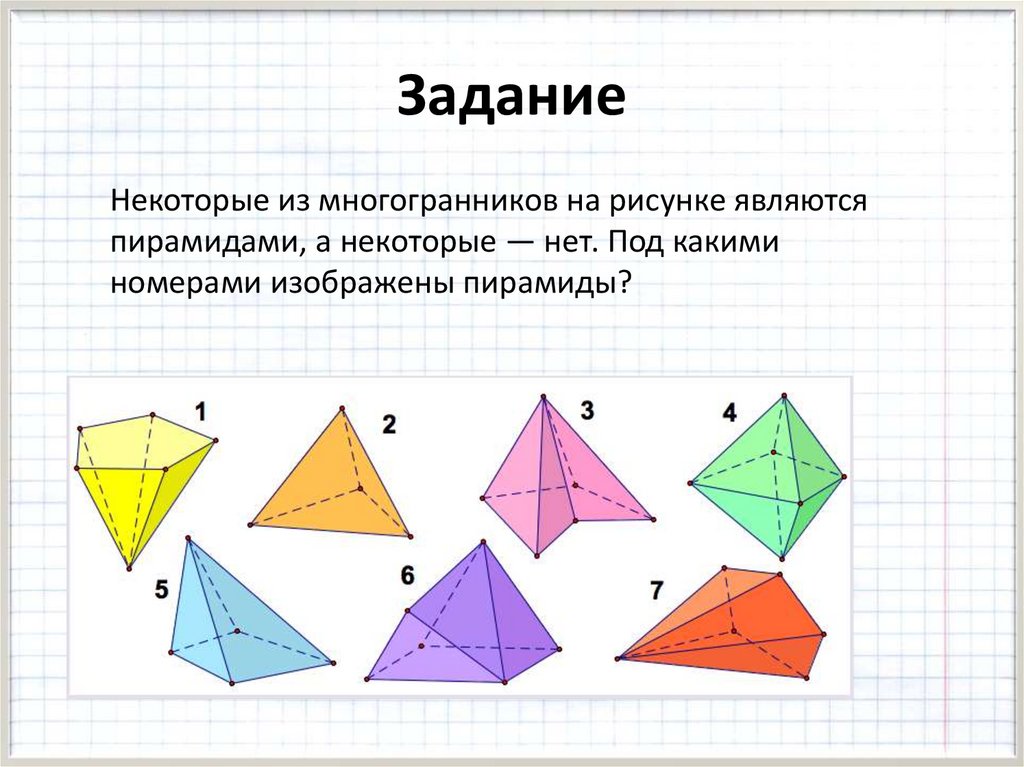
Задание
Некоторые из многогранников на рисунке являются
пирамидами, а некоторые — нет. Под какими
номерами изображены пирамиды?

15.

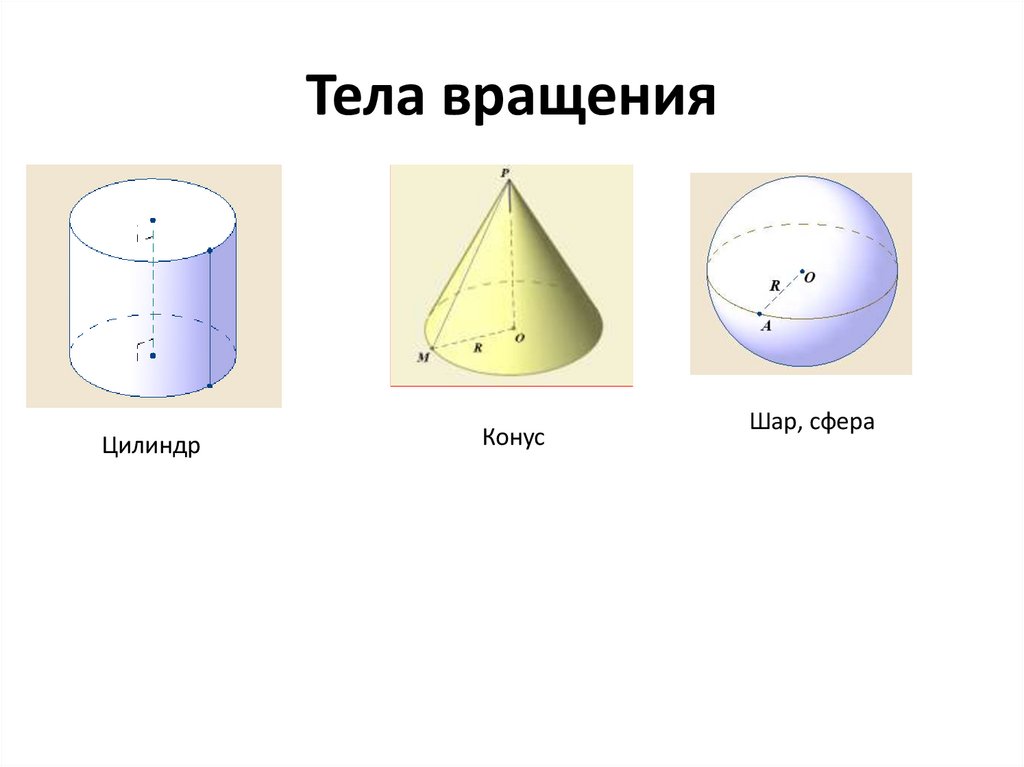
Тела вращения
Тело вращения- это фигура, полученная
вращением плоского многоугольника
вокруг оси.

16.

Тела вращения
Цилиндр
Конус
Шар, сфера

17.

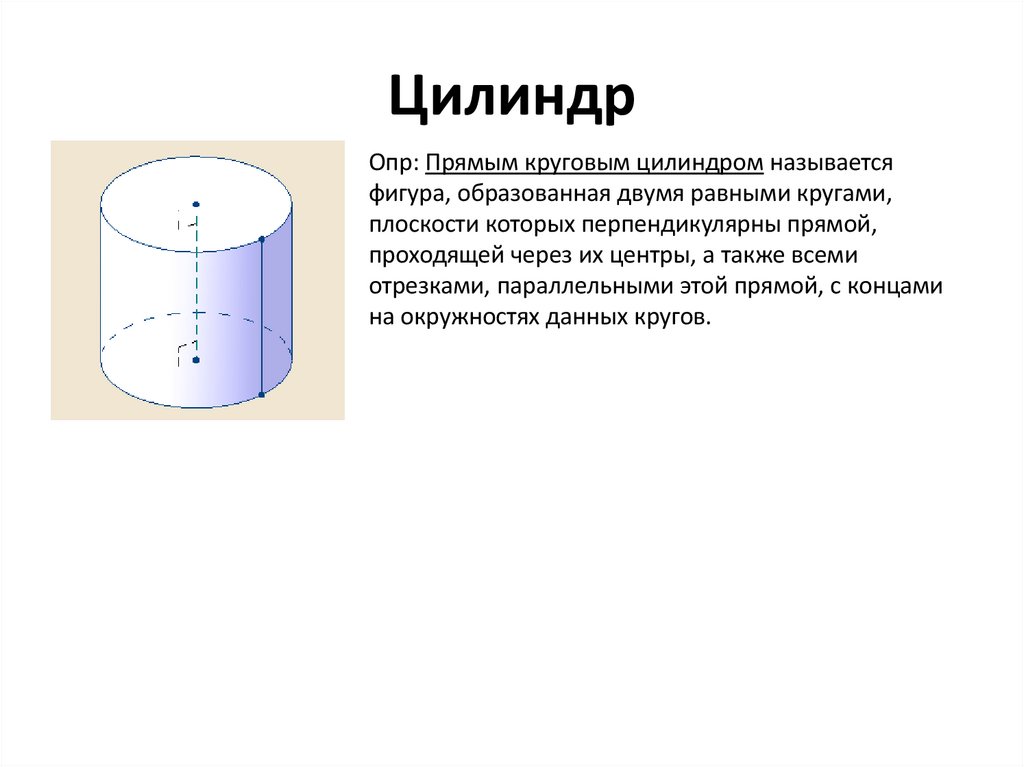
Цилиндр
Опр: Прямым круговым цилиндром называется
фигура, образованная двумя равными кругами,
плоскости которых перпендикулярны прямой,
проходящей через их центры, а также всеми
отрезками, параллельными этой прямой, с концами
на окружностях данных кругов.

18.

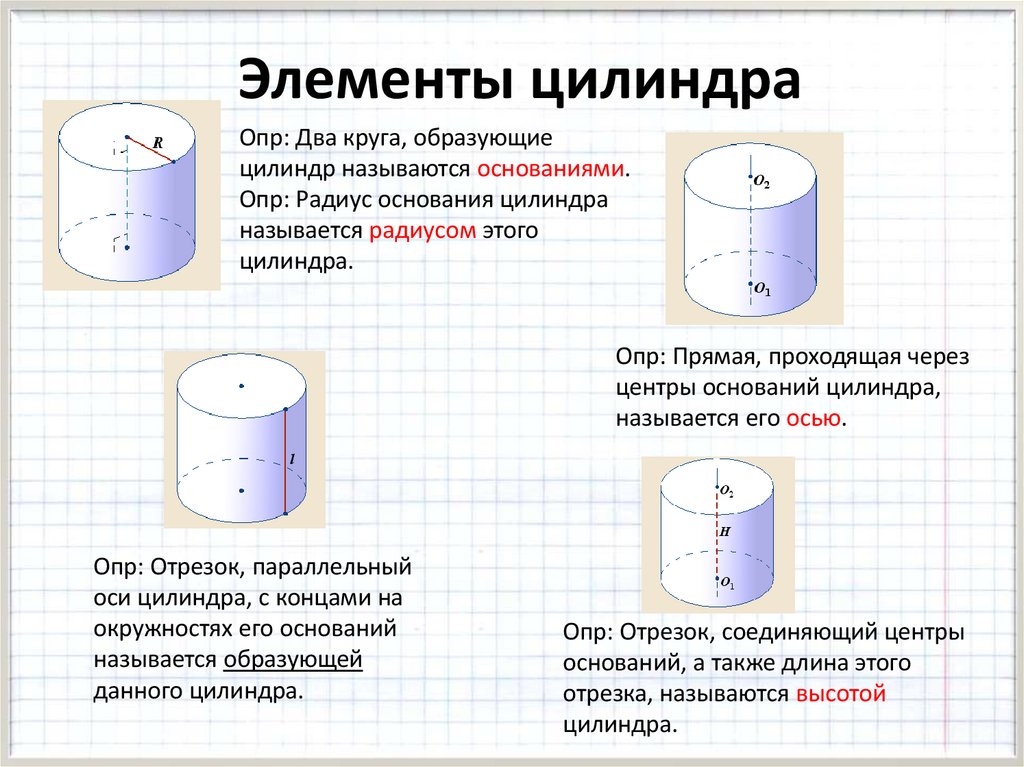
Элементы цилиндра
Опр: Два круга, образующие
цилиндр называются основаниями.
Опр: Радиус основания цилиндра
называется радиусом этого
цилиндра.
Опр: Прямая, проходящая через
центры оснований цилиндра,
называется его осью.
Опр: Отрезок, параллельный
оси цилиндра, с концами на
окружностях его оснований
называется образующей
данного цилиндра.
Опр: Отрезок, соединяющий центры
оснований, а также длина этого
отрезка, называются высотой
цилиндра.

19.

Сечения цилиндра

20.

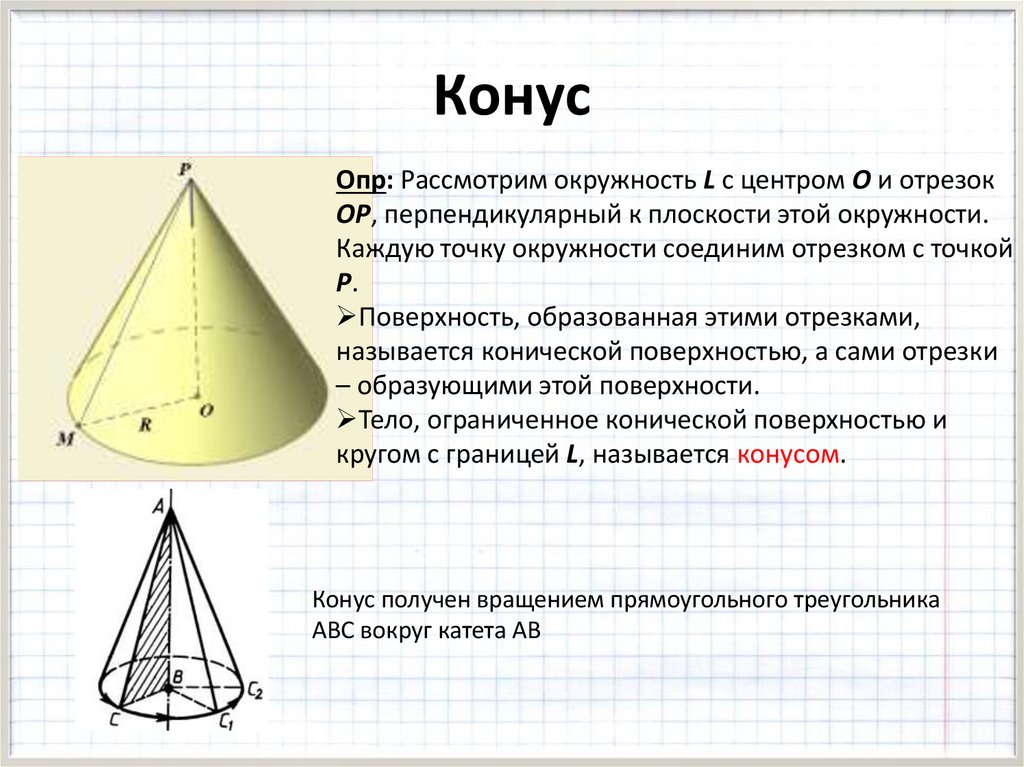
Конус
Опр: Рассмотрим окружность L с центром O и отрезок
OP, перпендикулярный к плоскости этой окружности.
Каждую точку окружности соединим отрезком с точкой
P.
Поверхность, образованная этими отрезками,
называется конической поверхностью, а сами отрезки
– образующими этой поверхности.
Тело, ограниченное конической поверхностью и
кругом с границей L, называется конусом.
Конус получен вращением прямоугольного треугольника
АВС вокруг катета АВ

21.

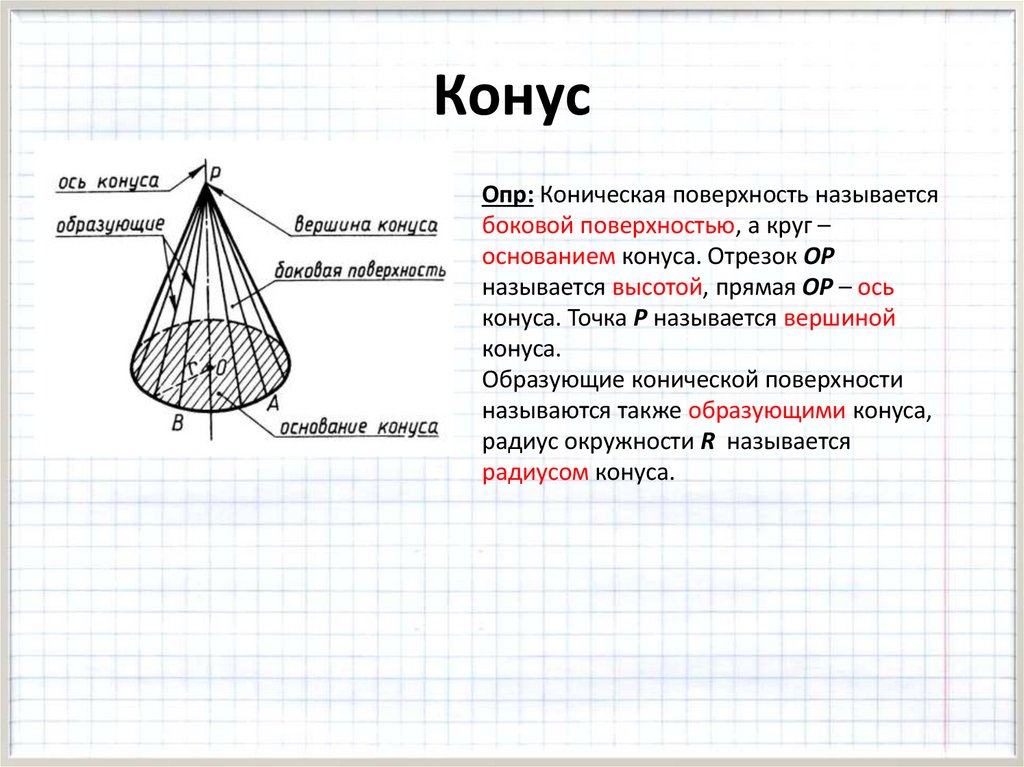
Конус
Опр: Коническая поверхность называется
боковой поверхностью, а круг –
основанием конуса. Отрезок OP
называется высотой, прямая OP – ось
конуса. Точка Р называется вершиной
конуса.
Образующие конической поверхности
называются также образующими конуса,
радиус окружности R называется
радиусом конуса.

22.

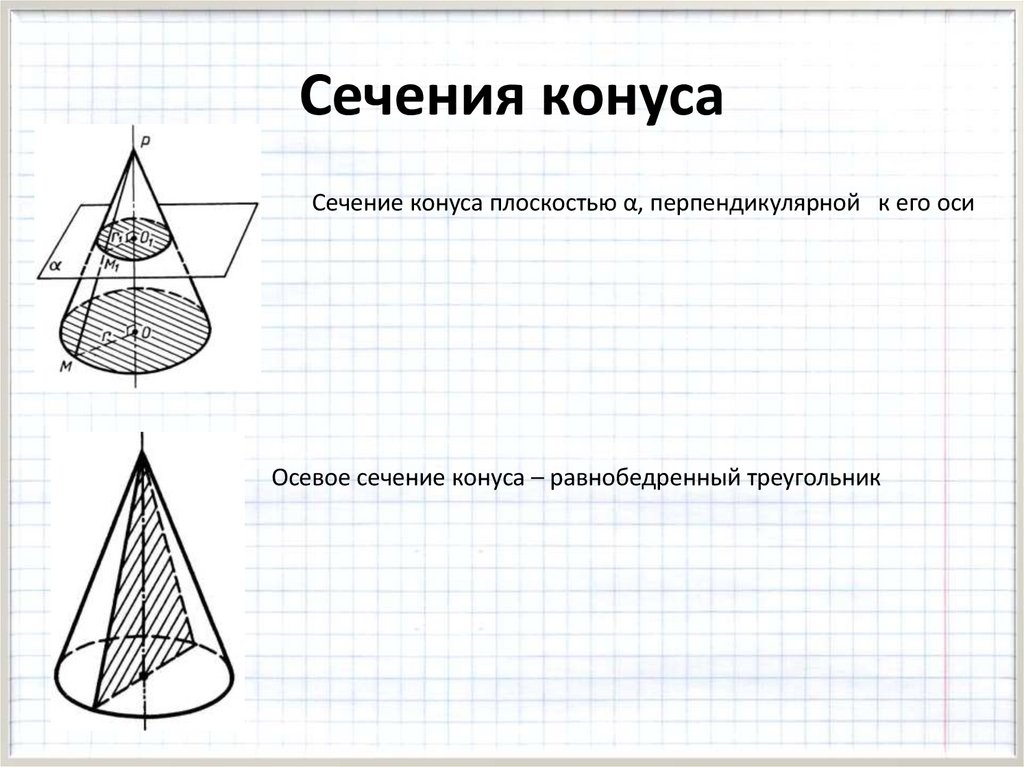
Сечения конуса
Сечение конуса плоскостью α, перпендикулярной к его оси
Осевое сечение конуса – равнобедренный треугольник

23.

Сфера
Опр: Сферой называется множество точек пространства,
равноудаленных от заданной точки. Эта точка называется
центром сферы.
Опр: Отрезок, соединяющий любую точку сферы и ее
центр, а также длина этого отрезка называются радиусом
сферы.
Шаром называется фигура, состоящая из сферы и множества всех ее
внутренних точек.
Сфера называется границей или поверхностью шара, а центр сферы
– центром шара.

24.

Сфера
Точки, расстояние от которых до центра сферы меньше
ее радиуса, называются внутренними точками сферы.
Точки, расстояние от которых до центра сферы
больше ее радиуса, называются внешними точками
сферы.

25.

Сфера
Отрезок, соединяющий две точки сферы, называется
хордой сферы (шара).
Любая хорда, проходящая через центр сферы,
называется диаметром сферы (шара).