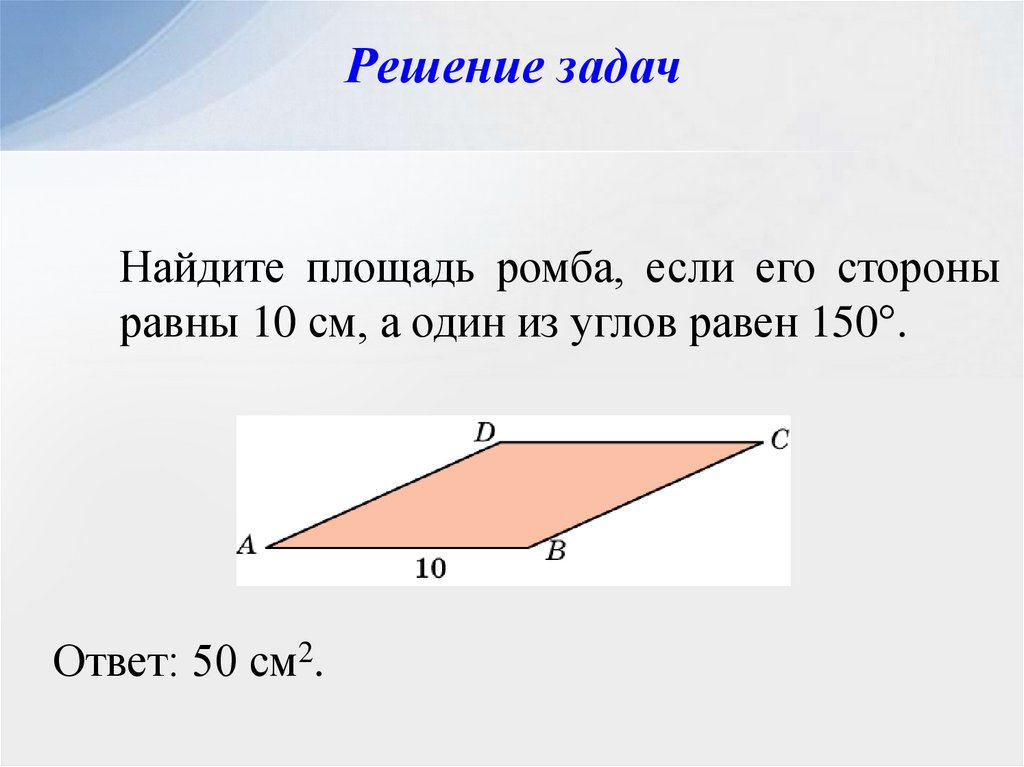
Площади параллелограмма и ромба

1.

21.01
Площади параллелограмма
и ромба

2.

Цели урока
Учащийся будет:
знать:
формулы площади параллелограмма, ромба.
уметь:
выводить и применять формулы площади
параллелограмма, ромба.

3.

Критерии оценивания
Учащийся:
знает:
формулы площади параллелограмма, ромба.
умеет:
выводить и применять формулы площади
параллелограмма, ромба.

4.

Проверка домашнего задания.
5. Дано: АВСД – параллелограмм.
АД=ВС=15, АВ=СД=10, ∠А=60°.
Найти S-?
Решение:
S=АВ*АД*sinA
3
S=10*15*sin60=150* = 75
2
2
Ответ: 75 3см
3
6. Дано: АВСД – параллелограмм.
АД=ВС=8, АВ=СД=5, АЕ=3, ВЕвысота
Найти S-?
Решение:
S=АД*ВЕ
ВЕ2 = АВ2 − АЕ2
ВЕ2 = 52 − 32 = 25 − 9 = 16
ВЕ=4
S=8*4=32см2
Ответ: 32см2
9. Дано: АВСД – ромб
АС=8, ВД=5.
Найти S-?
Решение:
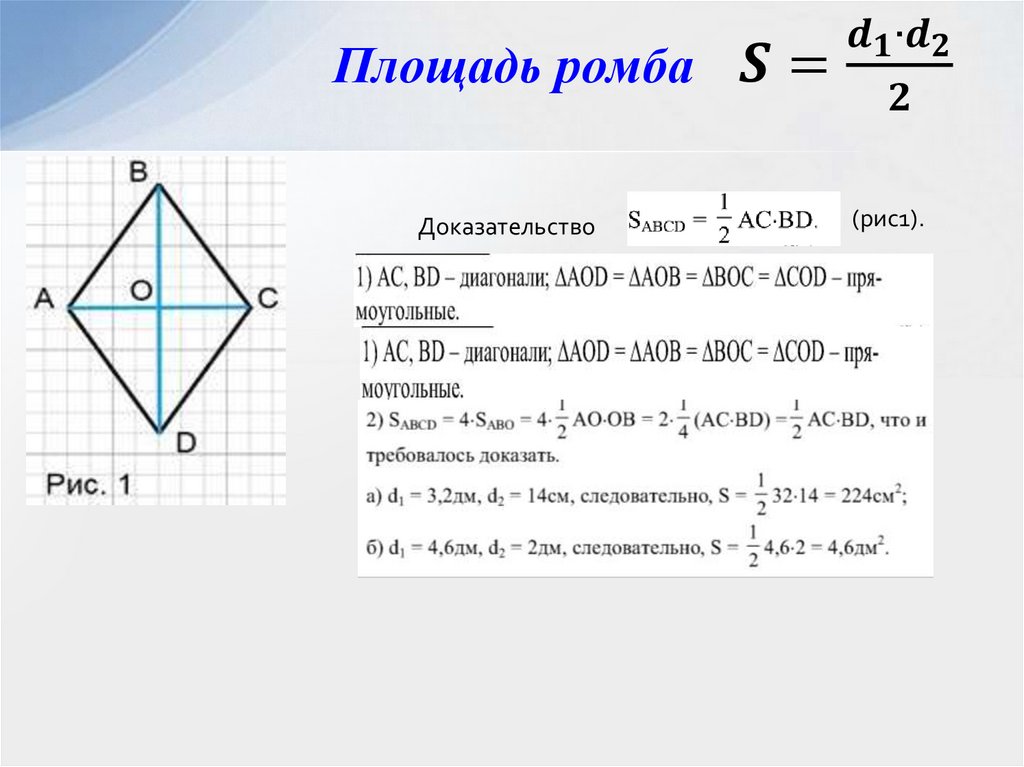
АС∗ВД
S=
2
8∗5
S= = 20 см2
2
Ответ: 20 см2
10. Дано: АВСД – параллелограмм.
АД=ВС=14, АВ=СД=5, АЕ=3, ВЕвысота
Найти S-?
Решение:
S=АД*ВЕ
ВЕ2 = АВ2 − АЕ2
ВЕ2 = 52 − 42 = 25 − 14 =9
ВЕ=3
S=14*3=42см2
Ответ: 42см2

5.

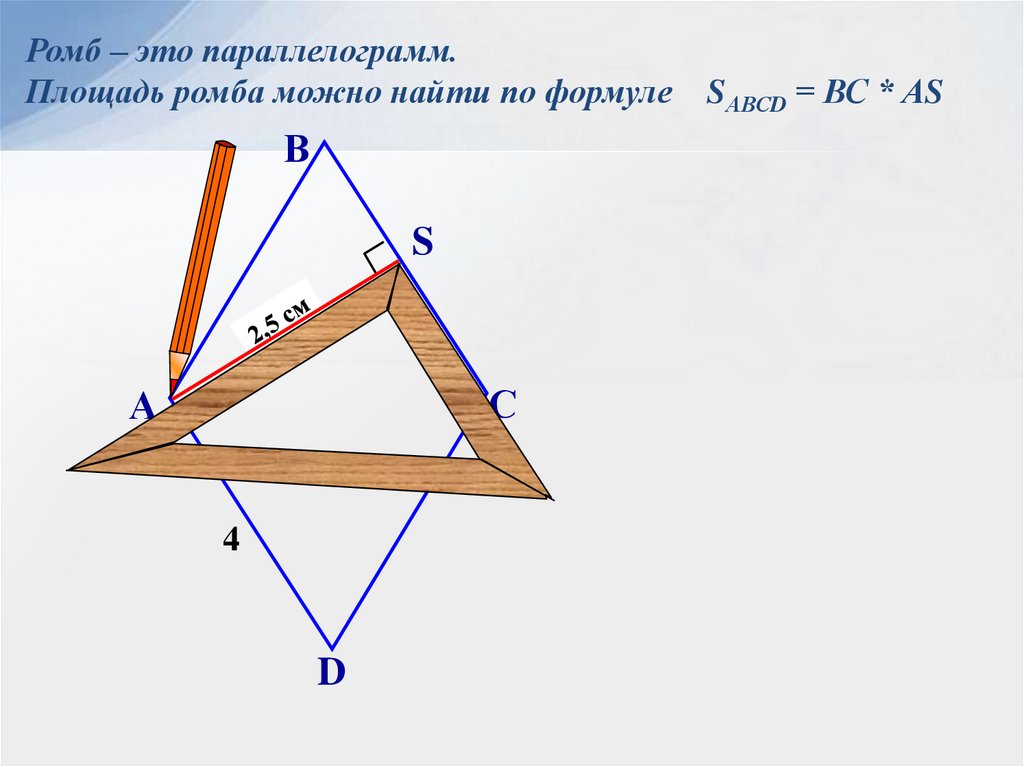
Ромб – это параллелограмм.
Площадь ромба можно найти по формуле
В
S
С
А
4
D
SАВСD = ВС * АS

6.

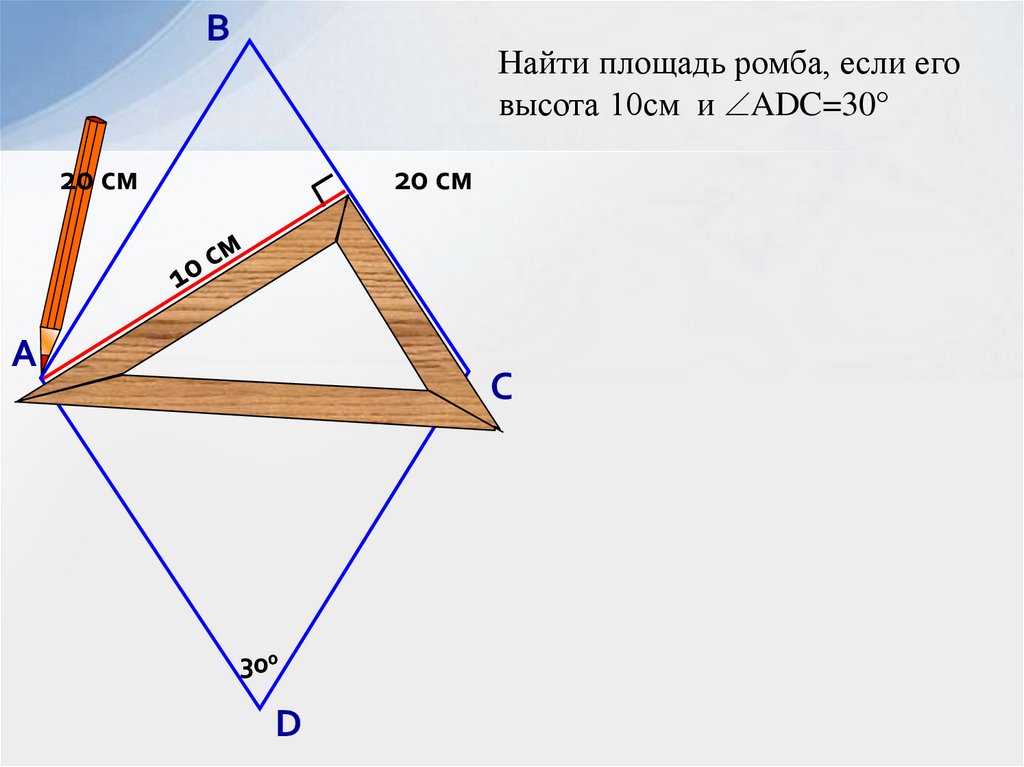
В
Найти площадь ромба, если его
высота 10см и ADC=30
20 см
20 см
А
С
300
D

7.

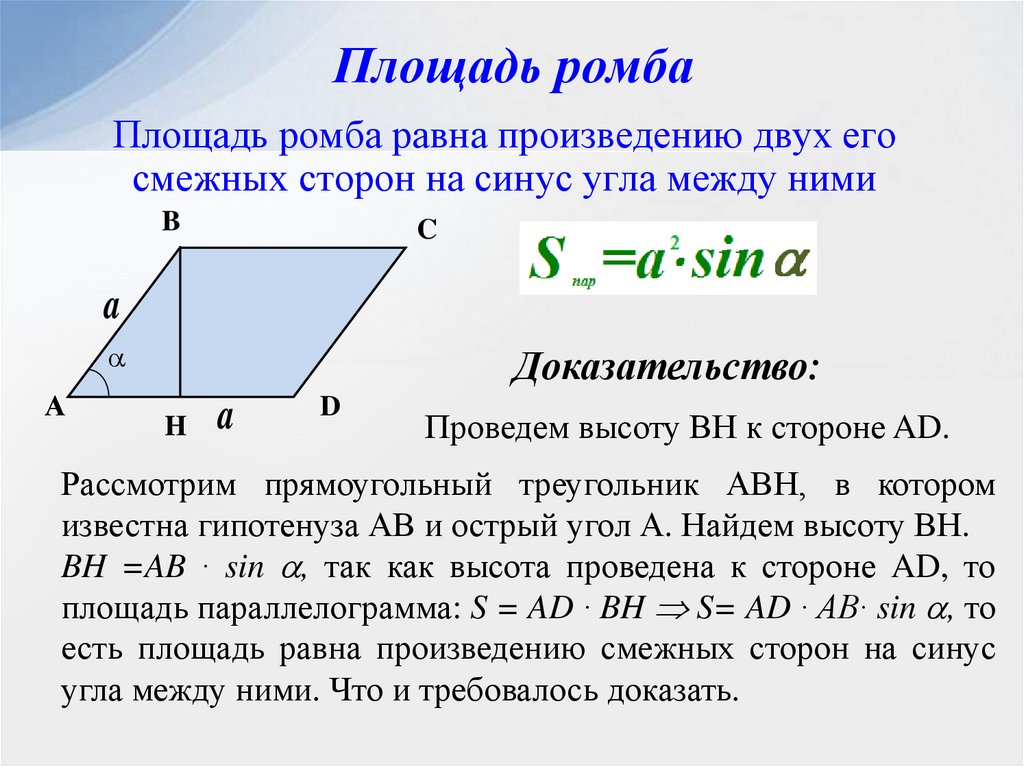
Площадь ромба
Площадь ромба равна произведению двух его
смежных сторон на синус угла между ними
B
C
a
А
Доказательство:
H
D
a
b
Проведем высоту ВН к стороне AD.
Рассмотрим прямоугольный треугольник АВН, в котором
известна гипотенуза
АВ и острый угол А. Найдем высоту ВН.
BH =AB ∙ sin , такbкак высота проведена к стороне AD, то
площадь параллелограмма: S = AD ∙ BH S= AD ∙ AB∙ sin , то
есть площадь равна произведению смежных сторон на синус
угла между ними. Что и требовалось доказать.

8.

Площадь ромба