Similar presentations:
Задачи и методы многомерного статистического анализа в экономике
1. Основной курс Тема 1. Задачи и методы многомерного статистического анализа в экономике .
1. Теоретические основы многомерногостатистического анализа.
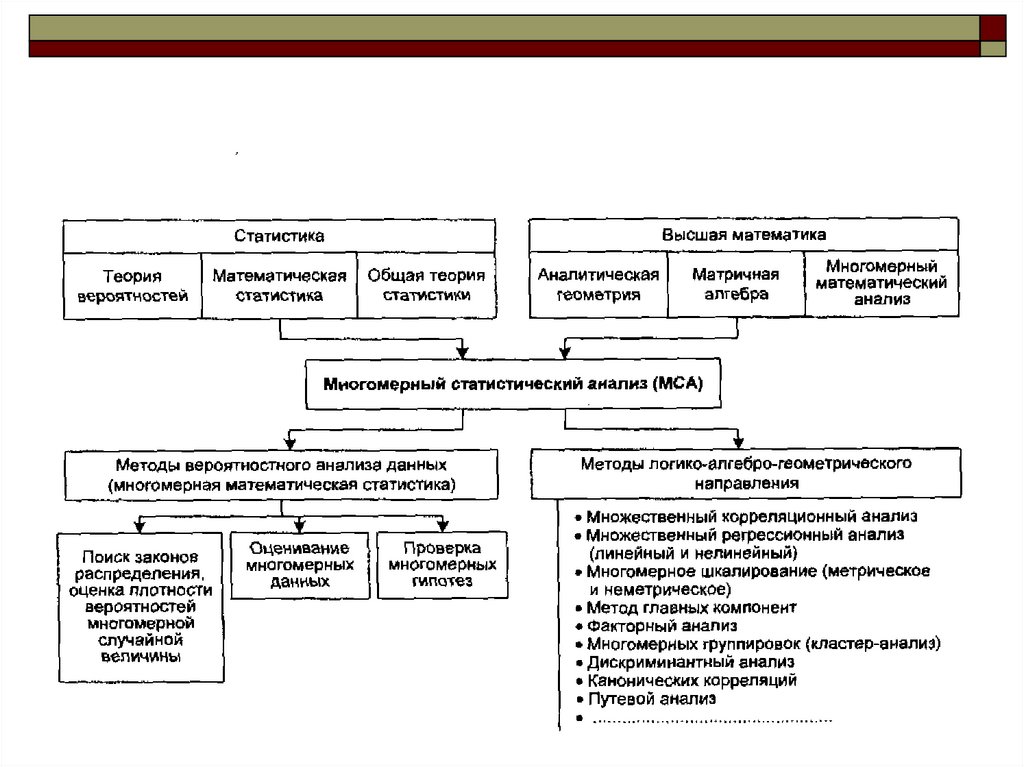
2. Методы многомерного статистического анализа.
3. Многомерное признаковое пространство.
Особенности обработки многомерных статистических
данных.
4. Выборочное наблюдение
2. 1. Теоретические основы многомерного статистического анализа.
Многомерный статистический анализ совокупность формализованных статистическихметодов, базирующихся на представлении исходной
информации в многомерном геометрическом
пространстве и позволяющих определять неявные
(латентные), но объективно существующие
закономерности в организационной структуре и
тенденциях развития изучаемых социальноэкономических явлений и процессов.
3.
Для МСА как самостоятельной области наукихарактерны следующие особенности:
Методы МСА в отличие от классической статистики появились
сравнительно недавно: факторный анализ — на рубеже XIX и XX вв.,
многомерное шкалирование — в конце 30-х — в 40-х годах нашего
столетия, кластер-анализ — 10—20-е годы и т.д. Основная часть
методов еще находится в стадии активной разработки, область их
применения четко не разграничена. Отсутствуют строгие рекомендации
по приложению этих методов в решении большого числа конкретных
ситуационных задач.
Для методов МСА характерны, формализация, сложная логикоматематическая конструкция.
Применение методов МСА требует нетрадиционного подхода к
решению аналитических задач.
4.
В МСА обрабатываются многомерные (многопризнаковые)совокупности данных. Число признаков (или размерность совокупности)
при этом может быть любым — от 1 до 100 и более.
Практическое применение методов МСА требует обязательного
использования вычислительной техники. Можно сказать, что эти методы
в силу сложности и трудоемкости нереализуемы без технических
средств.
5.
Американская школа — факторный анализ, многомерноешкалирование, концепции новейшей статистической теории:
размытых множеств, путевого анализа и т.п., многомерная
математическая статистика;
Английская школа — факторный анализ; дискриминантный
анализ, многомерный корреляционно-регрессионный анализ,
многомерная математическая статистика;
Французская школа — кластер-анализ.
6.
2. Методы многомерного статистического анализа.Предметом в МСА являются структура, закономерности
формирования и развития сложных социальных и экономических
явлений и процессов в их многоаспектной качественной
определенности в статике и динамике.
Объектом исследования в МСА могут быть отдельные
предприятия, отрасли и народное хозяйство в целом, социальноэкономические процессы или явления. Во всех случаях исходная
статистическая совокупность должна представлять массовую
категорию, измеренную и выраженную системой показателей.
Особенностью методологии МСА является необходимость
выполнения сложного шкалирования исходной статистической
совокупности,
соединения
методов
общей
теории
и
математической статистики, интерпретация результатов анализа.
7.
8.
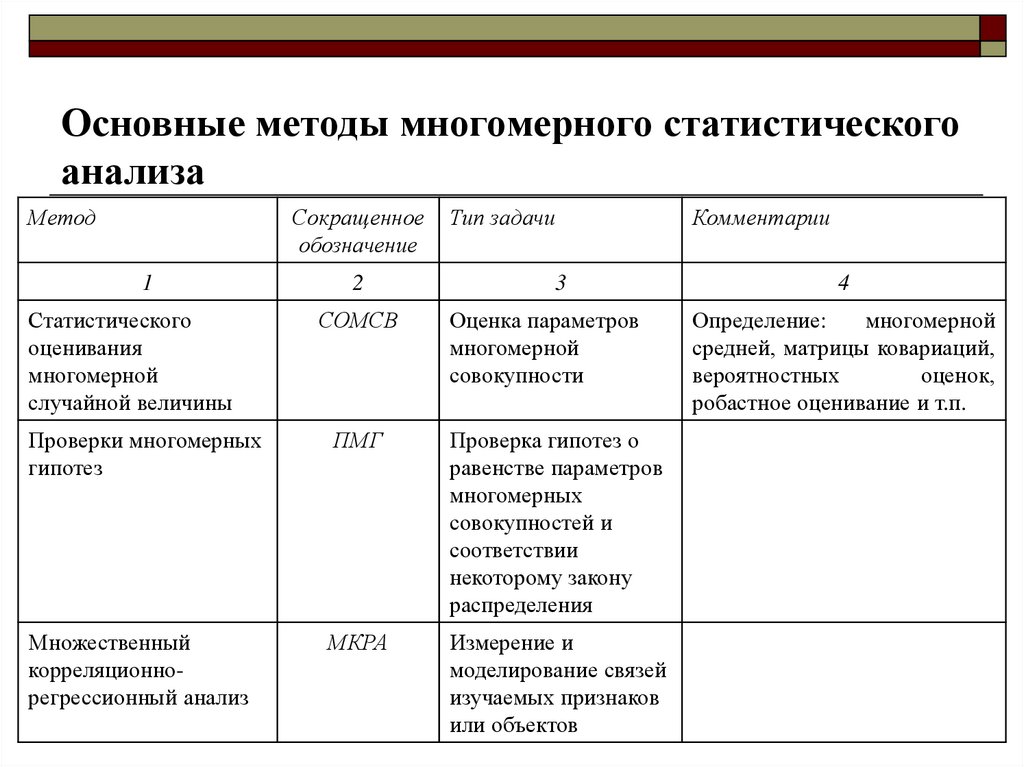
Основные методы многомерного статистическогоанализа
Метод
Сокращенное
обозначение
1
2
Тип задачи
3
Статистического
оценивания
многомерной
случайной величины
СОМСВ
Оценка параметров
многомерной
совокупности
Проверки многомерных
гипотез
ПМГ
Проверка гипотез о
равенстве параметров
многомерных
совокупностей и
соответствии
некоторому закону
распределения
Множественный
корреляционнорегрессионный анализ
МКРА
Измерение и
моделирование связей
изучаемых признаков
или объектов
Комментарии
4
Определение:
многомерной
средней, матрицы ковариаций,
вероятностных
оценок,
робастное оценивание и т.п.
9.
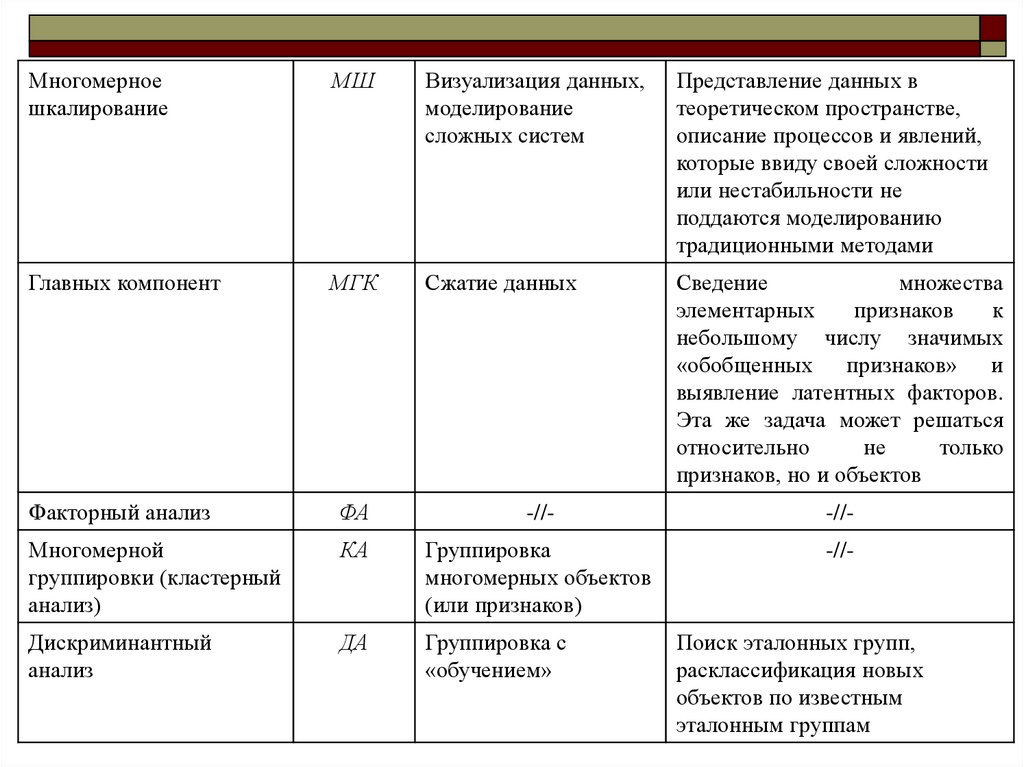
Многомерноешкалирование
МШ
Визуализация данных,
моделирование
сложных систем
Представление данных в
теоретическом пространстве,
описание процессов и явлений,
которые ввиду своей сложности
или нестабильности не
поддаются моделированию
традиционными методами
Главных компонент
МГК
Сжатие данных
Сведение
множества
элементарных
признаков
к
небольшому числу значимых
«обобщенных признаков» и
выявление латентных факторов.
Эта же задача может решаться
относительно
не
только
признаков, но и объектов
Факторный анализ
ФА
-//-
-//-
Многомерной
группировки (кластерный
анализ)
КА
Группировка
многомерных объектов
(или признаков)
-//-
Дискриминантный
анализ
ДА
Группировка с
«обучением»
Поиск эталонных групп,
расклассификация новых
объектов по известным
эталонным группам
10.
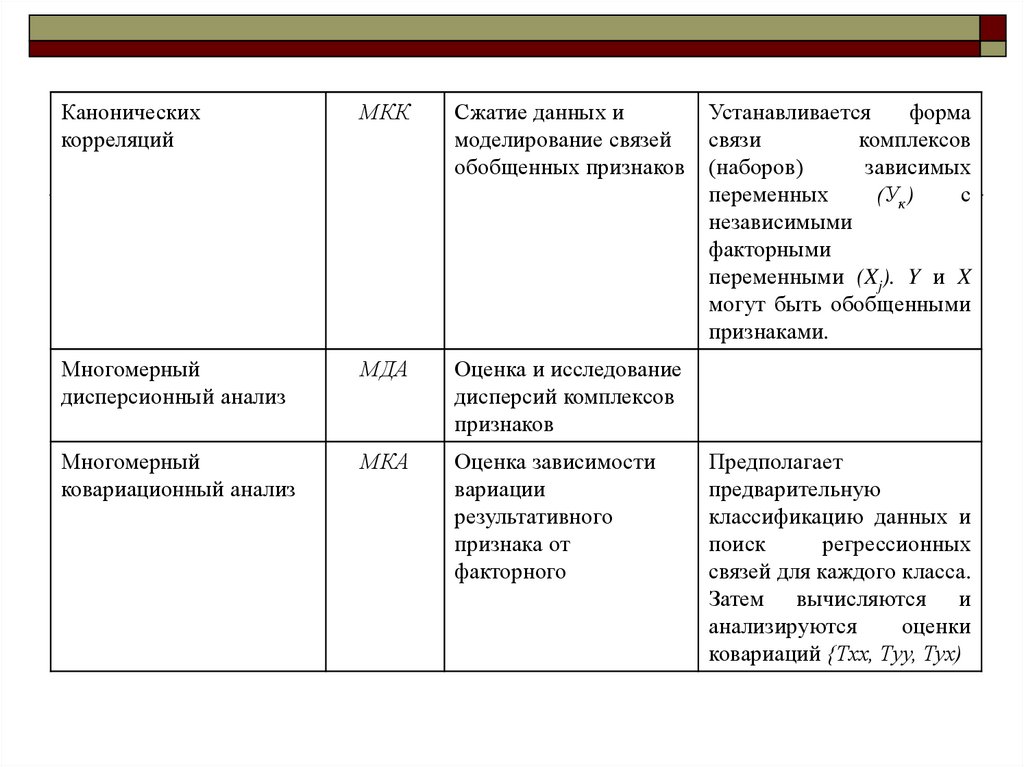
Каноническихкорреляций
МКК
Сжатие данных и
моделирование связей
обобщенных признаков
Многомерный
дисперсионный анализ
МДА
Оценка и исследование
дисперсий комплексов
признаков
Многомерный
ковариационный анализ
МКА
Оценка зависимости
вариации
результативного
признака от
факторного
Устанавливается
форма
связи
комплексов
(наборов)
зависимых
переменных
(Ук)
с
независимыми
факторными
переменными (Xj). Y и X
могут быть обобщенными
признаками.
Предполагает
предварительную
классификацию данных и
поиск
регрессионных
связей для каждого класса.
Затем вычисляются и
анализируются
оценки
ковариаций {Тхх, Туу, Тух)
11.
В основе практического применения методов МСА лежитряд основополагающих принципов:
1) эффекта существенной многомерности — изучению
подле жит не произвольный набор признаков или
объектов, а комплекс органично связанных и взаимно
дополняющих друг друга при знаков, которые позволяют
полно и всесторонне оценивать явление (процесс).
2) лаконичного описания наблюдаемых многомерных
объектов. Под этим понимается необходимость
максимально сжатого и строго структурированного
представления информации.
12.
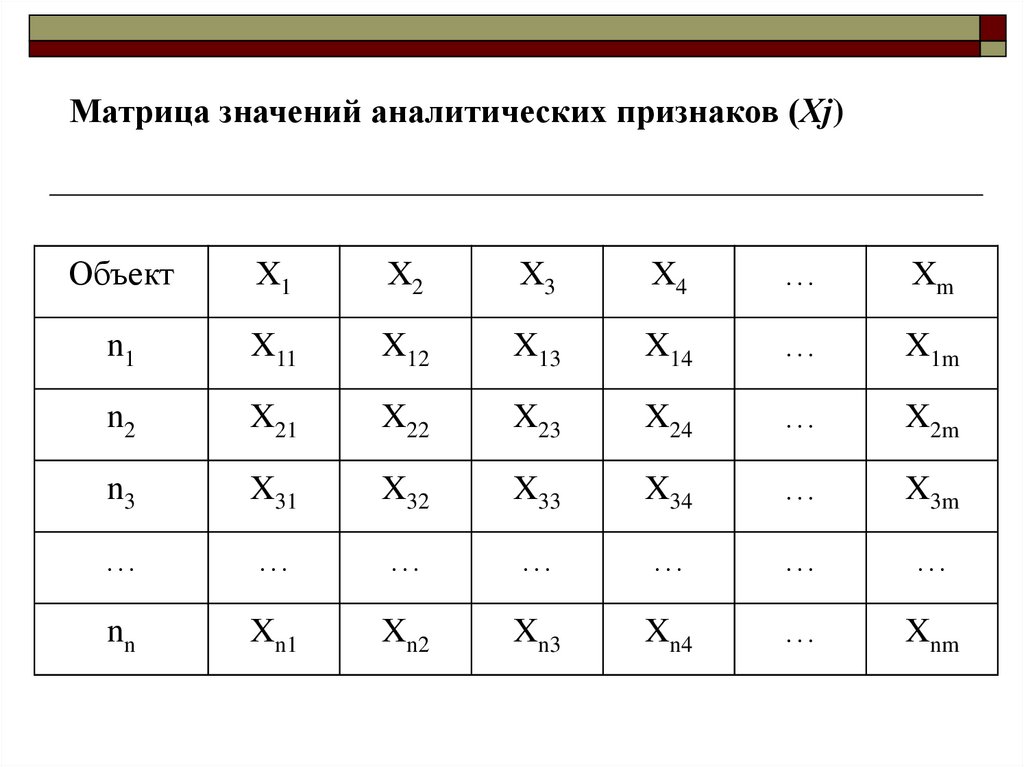
Матрица значений аналитических признаков (Хj)Объект
Х1
Х2
Х3
Х4
…
Хm
n1
X11
X12
X13
X14
…
X1m
n2
X21
X22
X23
X24
…
X2m
n3
X31
X32
X33
X34
…
X3m
…
…
…
…
…
…
…
nn
Xn1
Xn2
Xn3
Xn4
…
Xnm
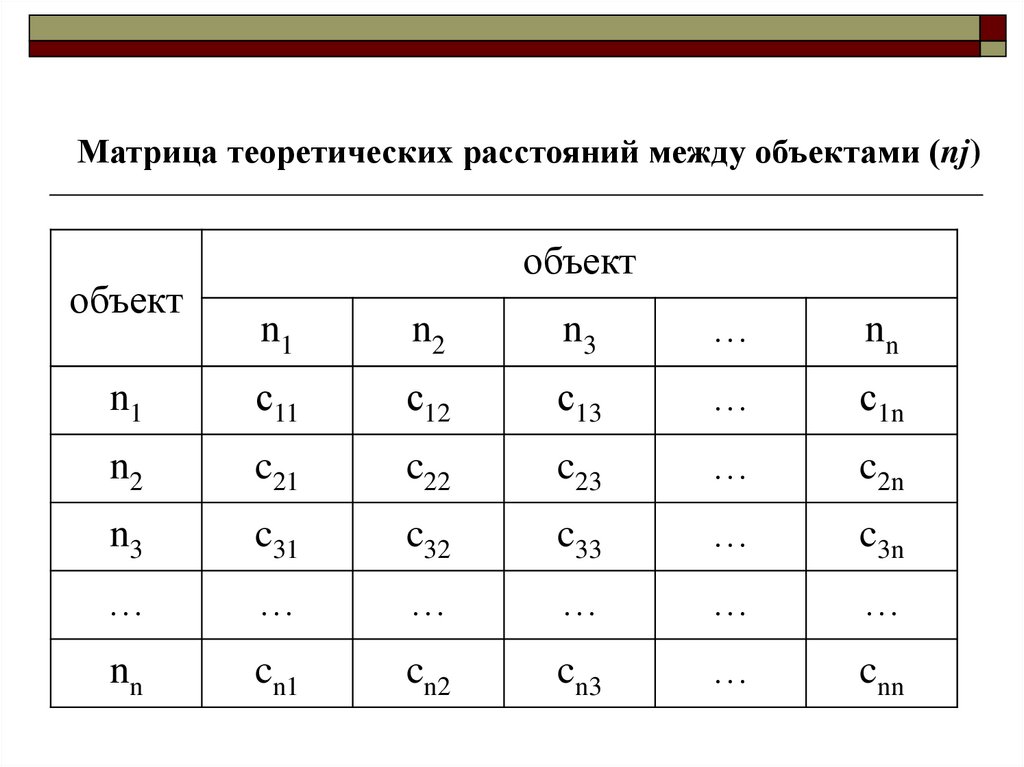
13.
Матрица теоретических расстояний между объектами (nj)объект
объект
n1
n2
n3
…
nn
n1
с11
с12
с13
…
с1n
n2
c21
c22
c23
…
c2n
n3
c31
c32
c33
…
c3n
…
…
…
…
…
…
nn
cn1
cn2
cn3
…
cnn
14.
3) максимального использования «обучения» в настройкематематических моделей, т.е. использование
информации, позволяющей наиболее точно
идентифицировать изучаемые объекты, соотнести их с
классом хорошо изученных явлений.
4) оптимизационной формулировки задач МСА. Имеется в
виду рациональный выбор из всего арсенала методов МСА
одного или нескольких дополняющих друг друга методов,
которые при минимуме вычислительной работы позволили
бы получить аналитические результаты с хорошей
интерпретируемостью, достаточно полно и достоверно
представляющие изучаемые явления (процессы).
15.
При реализации МСА можно выделить следующиеосновные этапы исследовательской работы::
формулировка задачи исследования на предметносодержательном уровне, определение объемов входной и
выходной информации, формы выходных данных;
определение последовательности обработки входной
информации методами МСА;
сбор и систематизация исходной информации для
последующей ее машинной обработки;
предварительный анализ данных: их однородности, соответствия
некоторым статистическим гипотезам, подчинения известным
законам распределения, содержания грубых ошибок и т.д ;
проведение вычислений ;
результаты анализа сводятся и оцениваются на адекватность при
помощи статистических критериев ;
обобщение и интерпретация результатов, формулировка
окончательных выводов и практических рекомендаций ;
16.
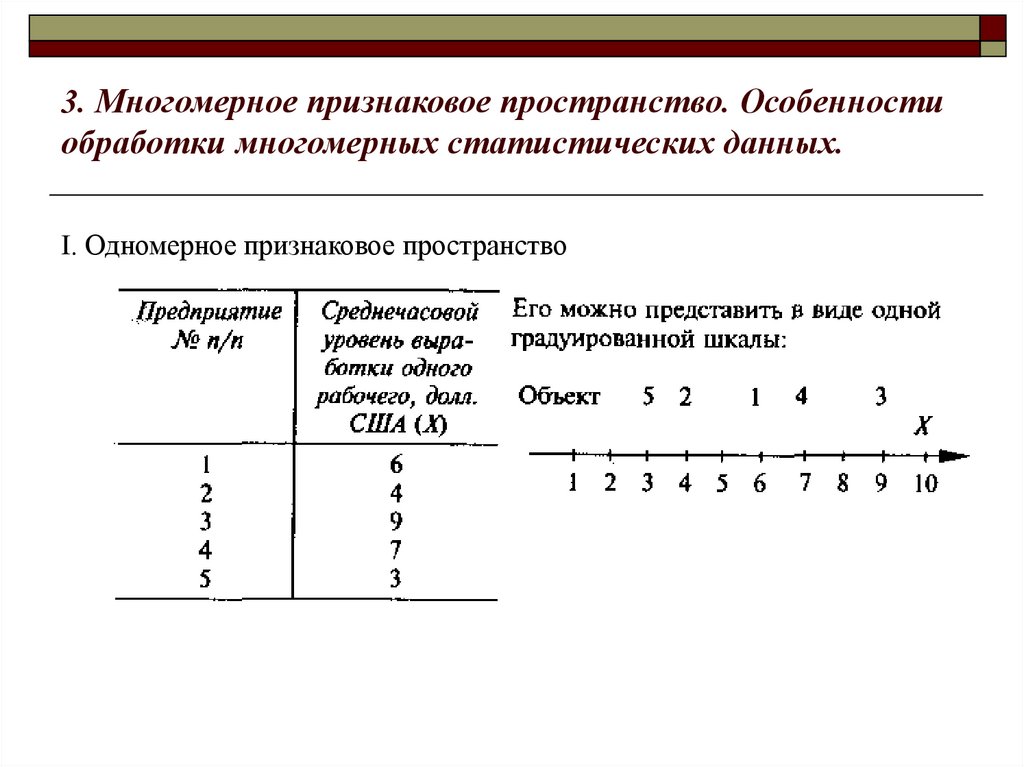
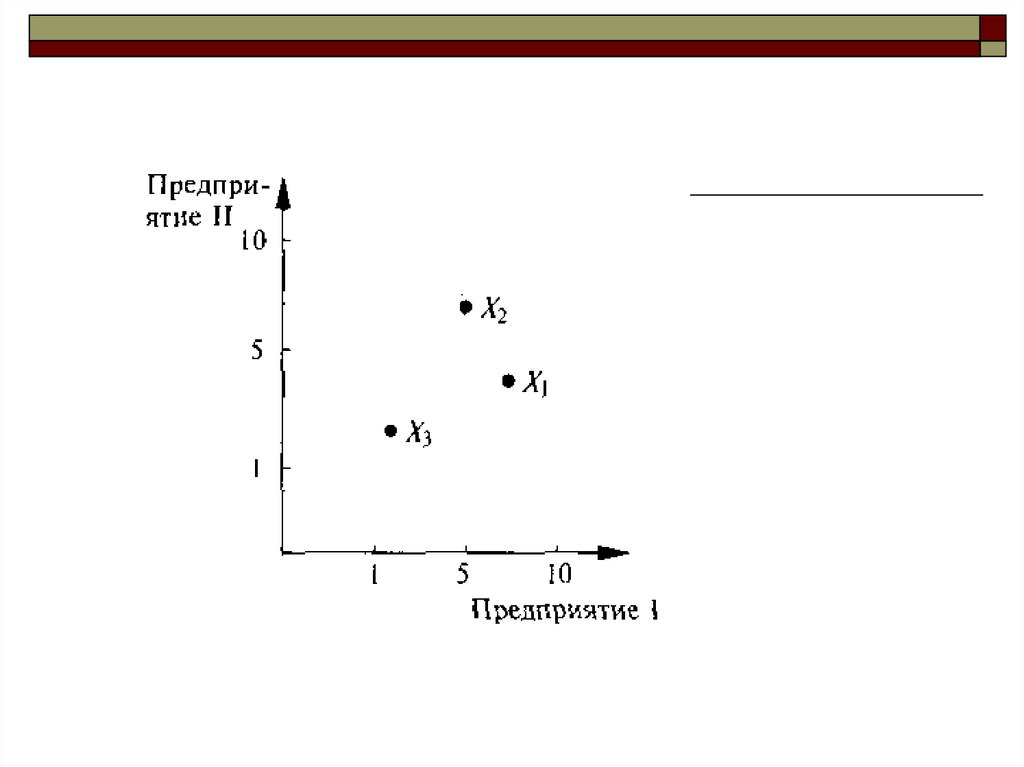
3. Многомерное признаковое пространство. Особенностиобработки многомерных статистических данных.
I. Одномерное признаковое пространство
17.
18.
III : Трехмерное признаковое пространствоНаблюдаемые объекты представляются в трехмерной системе координат
19.
20.
Размерность пространства описывается при помощисокращения французского слова dimension —
размерность, как dim U, т.е. размерность
пространства U.
21.
В аналитической работе при обращении к многомерномупространству признаков (объектов) принимаются во внимание
следующие особенности:
т-мерном пространстве сохраняют силу принципиальные
положения, аксиомы обычной евклидовой геометрии.
Например, в прямоугольной системе координат углы между
всеми парами осей составляют 90°, параллельные прямые,
плоскости и гиперплоскости не пересекаются, если квадрат
расстояния между двумя точками в двумерном пространстве
определяется по известной формуле Пифагора: с2=х12+х22, то в
многомерном пространстве — аналогичным
образом: с2=х12+х22+…+хр2
22.
пространство, размерность которого превышает три, ужене может быть представлено визуально, и все задачи в этом
случае решаются при помощи абстрактной логики и
алгебраических методов;
в многомерном анализе, как правило, используется
большое число признаков, разнородных по своей природе. В
связи с этим на первом этапе исследований обычно
возникает проблема приведения всех анализируемых
признаков к одному основанию — сопоставимому виду;
23.
обработка m-мерных совокупностей включает, как правило,большое число сложных и трудоемких для выполнения
арифметических операций, поэтому осуществляется на основе
пошаговых алгоритмов;
при работе с т-мерными данными совместно используются
чисто математические, абстрактные методы и методы
экономико-статистического анализа, ориентированные на
конкретные сферы приложения. Следует обращать внимание на
непротиворечивость результатов, получаемых различными
методами. Возникающие противоречия указывают на
нарушения логики решения экономической задачи и становятся
источником ошибочных выводов.
24.
4. Выборочное наблюдение.Причины использования выборочного
наблюдения:
Повышение точности данных.
Экономия материальных, трудовых,
финансовых ресурсов и времени..
Без выборки не обойтись, когда наблюдение
связано с порчей наблюдаемых объектов. На
выборке основаны маркетинговые
исследования, оценки качества поставок.
25.
Этапы выборочного обследования :1.
определение границ генеральной совокупности;
2.
разработка программы наблюдения и инструкций;
3.
определение основы для проверки выборки списка единиц генеральной совокупности,
сведений об их размещении и т.д.;
4.
установление допустимого размера погрешности
и определение объема выборки;
5.
определение выборочного наблюдения;
6.
установление сроков проведения наблюдения;
7.
определение потребности в кадрах для
проведения выборочного наблюдения, их
подготовка;
8.
оценка точности и достоверности данных
выборки, определение порядка их
распространения на генеральную совокупность.
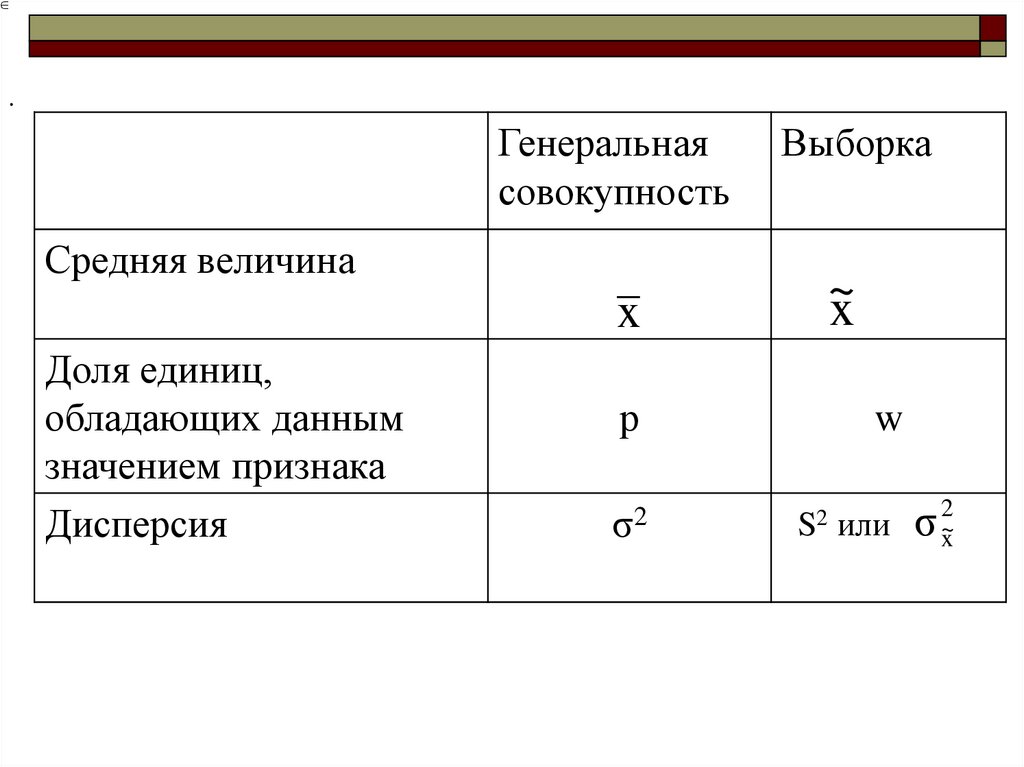
26.
.Генеральная
совокупность
Средняя величина
x
Доля единиц,
обладающих данным
значением признака
Дисперсия
Выборка
~
x
р
w
σ2
S2 или
σ
2
~
x
27.
.Способ отбора определяет конкретный
механизм или процедуру выборки единиц из
генеральной совокупности. В практике
используют следующие выборки:
• собственно случайная;
• механическая;
• типическая;
• серийная;
• комбинированная
28.
Ошибка выборки.
Теорема П.Л. Чебышева
n числа
При неограниченном увеличении
независимых наблюдений (
) в
генеральной совокупности с ограниченной
дисперсией с вероятностью сколь угодно
~
x
близкой к 1, можно ожидать,
что отклонение
выборочной средней
от генеральной
средней будет сколь угодно мало, т.е
~
P( x x ε) 1
29.
.Теорема А.М. Ляпунова
При достаточно большом числе независимых
наблюдений в генеральной совокупности с
конечной средней и ограниченной
дисперсией
~
x x
вероятность того, что
(расхождение между
выборочной средней и генеральной средней) не
превзойдет по абсолютной величине некоторую
величину t равно интегралу Лапласа:
~
P( x x tμ) Ф(t )
30.
t1
Ф(t )
e
2 π t
t2
2
t
2
dt
e
2π 0
t2
2
dt
31.
~εх х x
ε х2 σ σ
2
2
~
x
32.
με
f
2
i i
f
i
33.
μx2
~
(x i x) f i
f
i
34.
σμ
n
2
2
x
35.
σσ
μx
n
n
2
36.
~x x tμ
37.
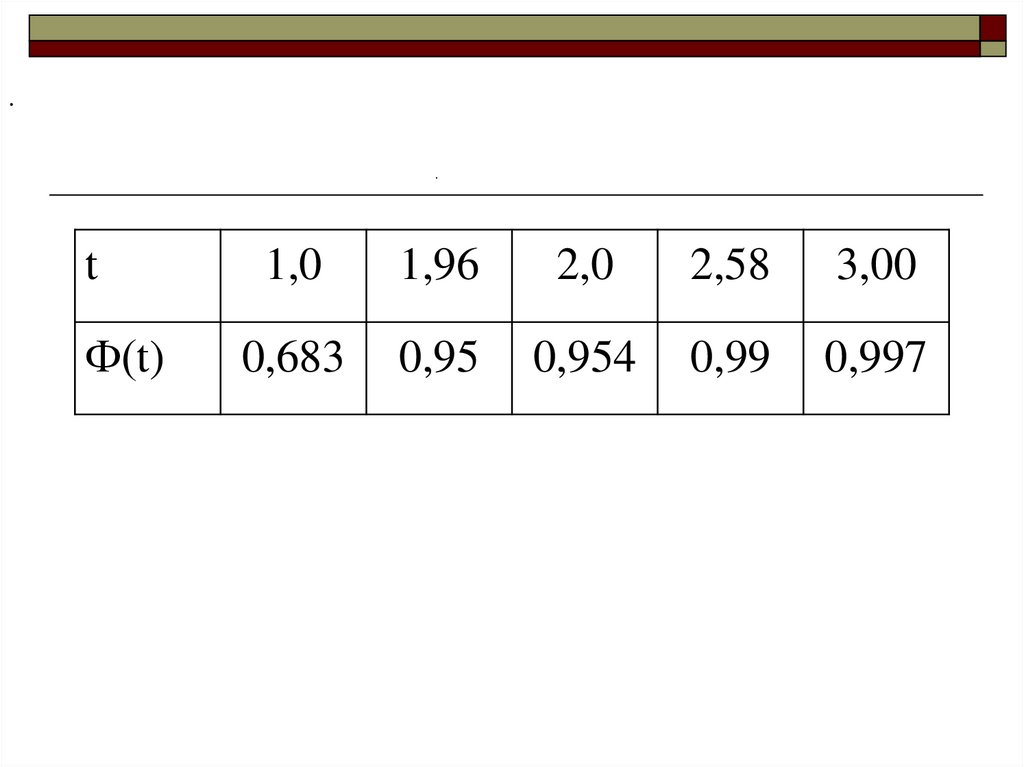
.t
1,0
1,96
2,0
2,58
3,00
Ф(t)
0,683
0,95
0,954
0,99
0,997
38.
n 1 2S
n
2
n
S
n 1
2
2
39.
2S
S
x
n 1
n 1
S
x
n
40.
Sx t x t
n
41.
w(1 w)μp
n
w (1 w)
p t μ p t
n
42.
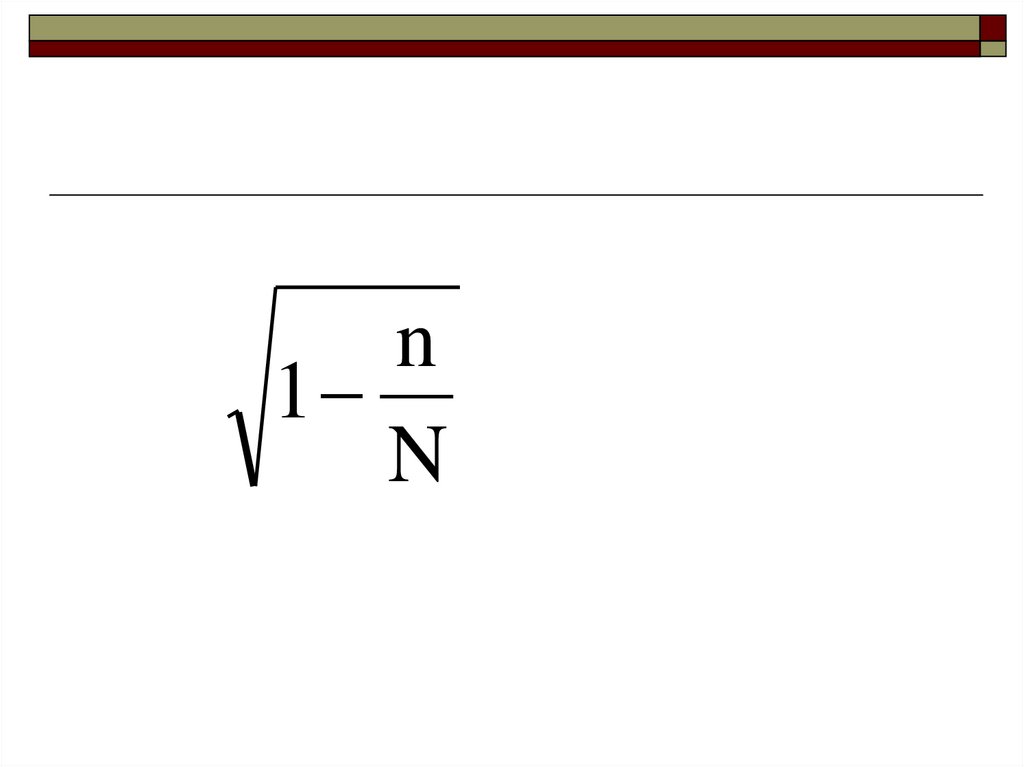
n1
N
43. Определение необходимой численности выборки.
tt
n
n
2
44.
tn 2
2
2
45.
σn
t
1
N
n
46.
Ntn
2
2 2
N t
2
2
47.
~~
x x x x x
p p p p p
48. Малая выборка
~x x
t
s /( n 1)
49.
sμ мв
n 1
50.
ns
2
~
(
x
x
)
i
i 1
n
51.
tS k (t , n) A 1
k
2
k 1
2
52.
k 1Г(
)
2
A
Г (k / 2) πk



















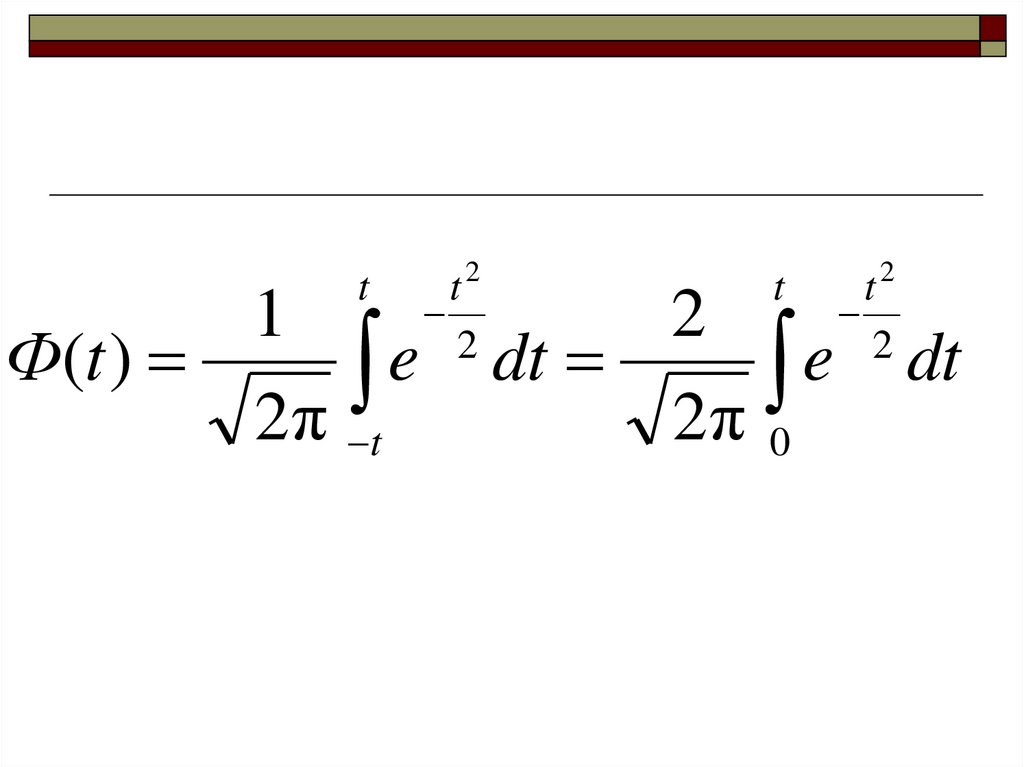
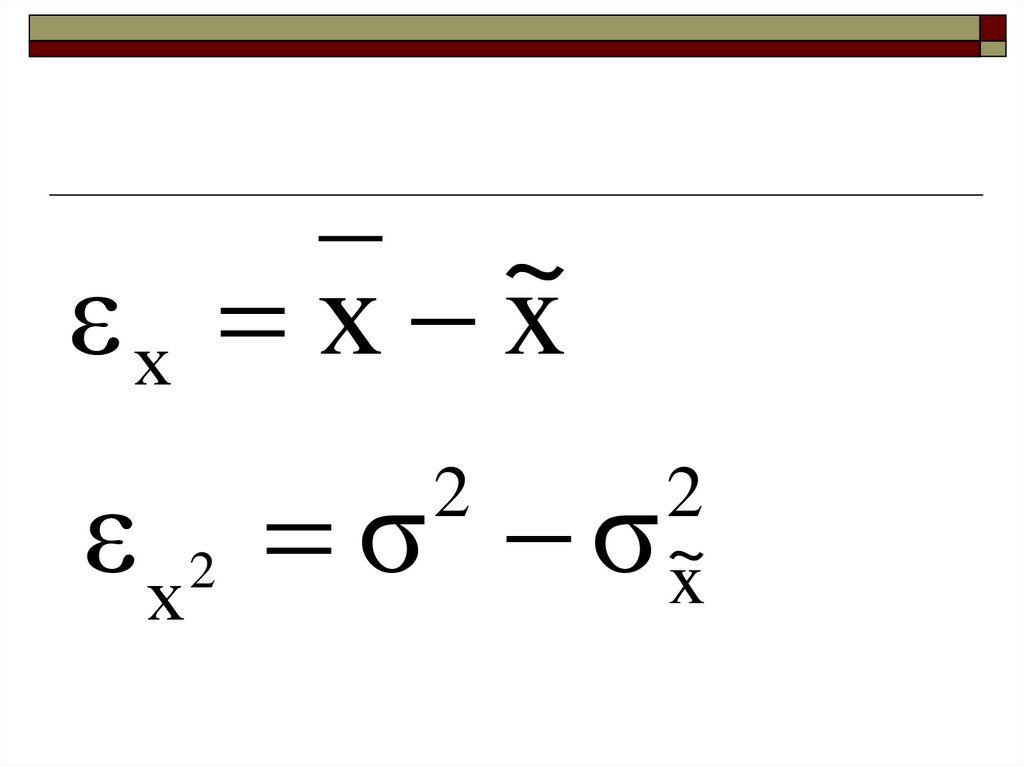
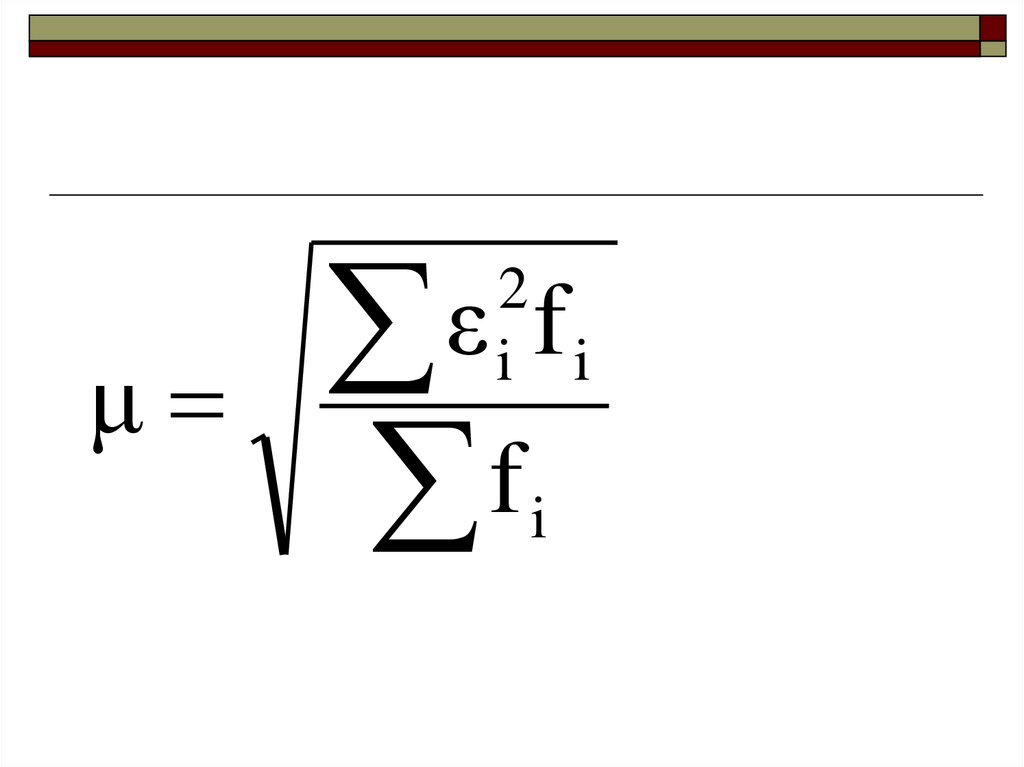
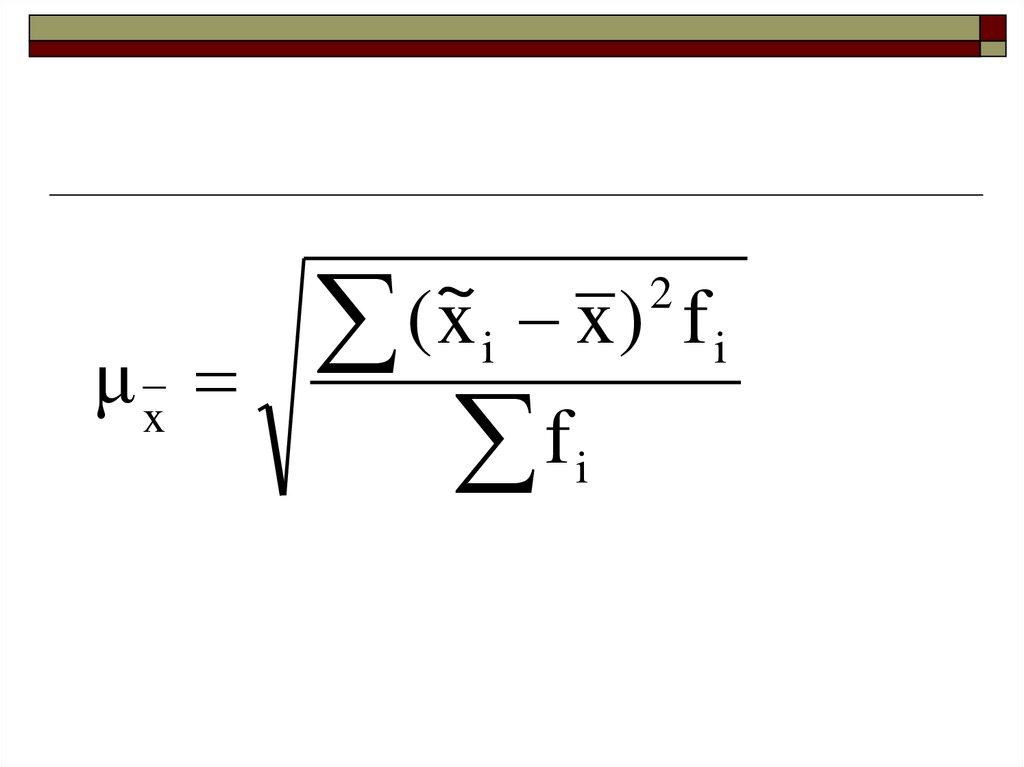
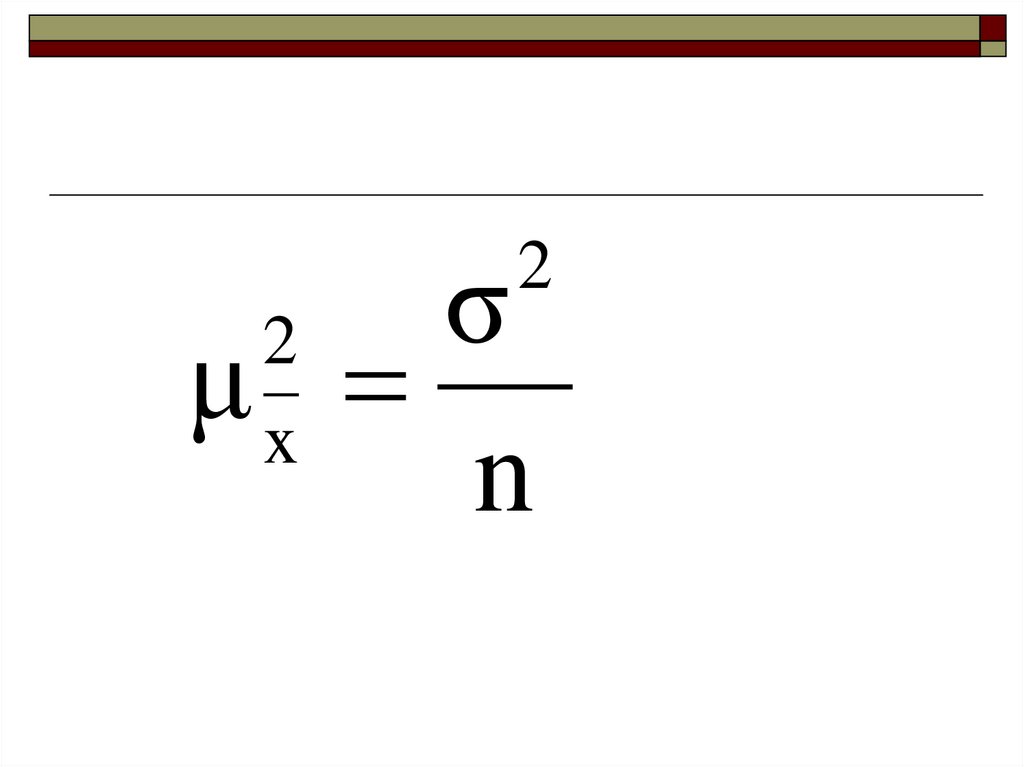
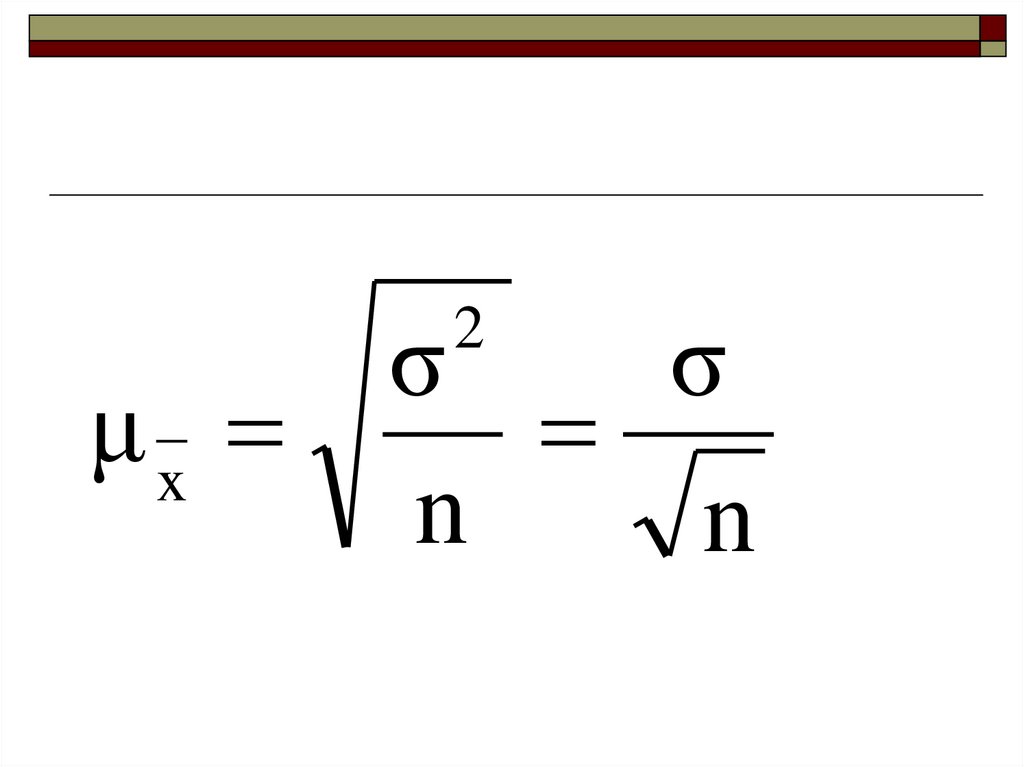
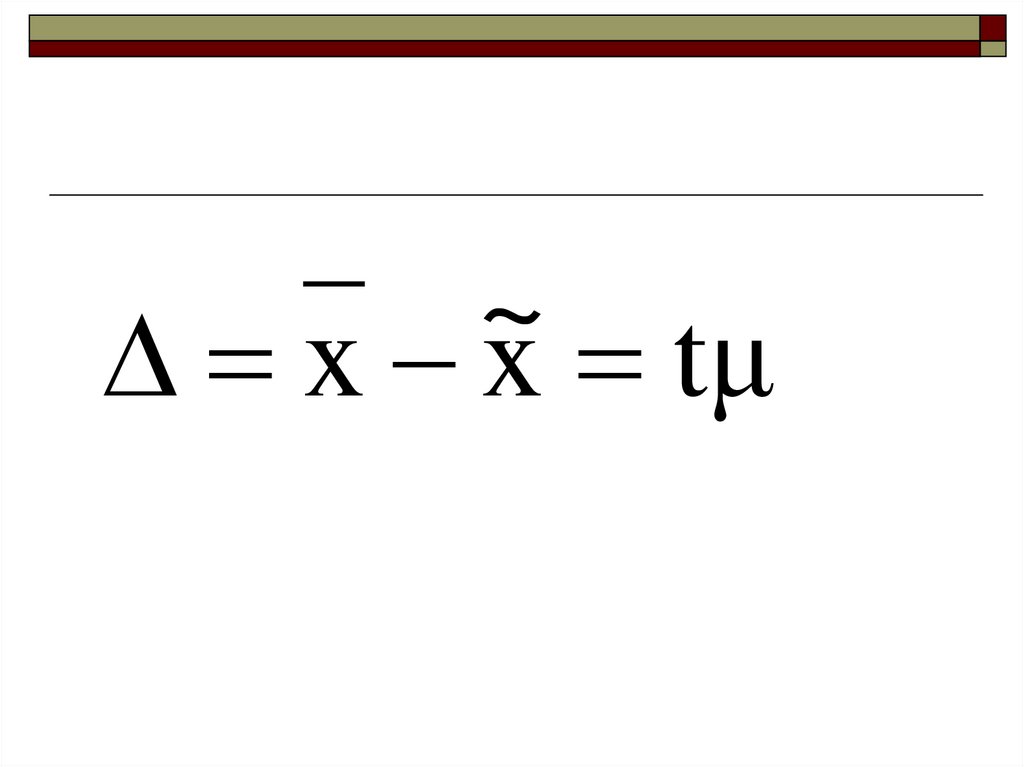
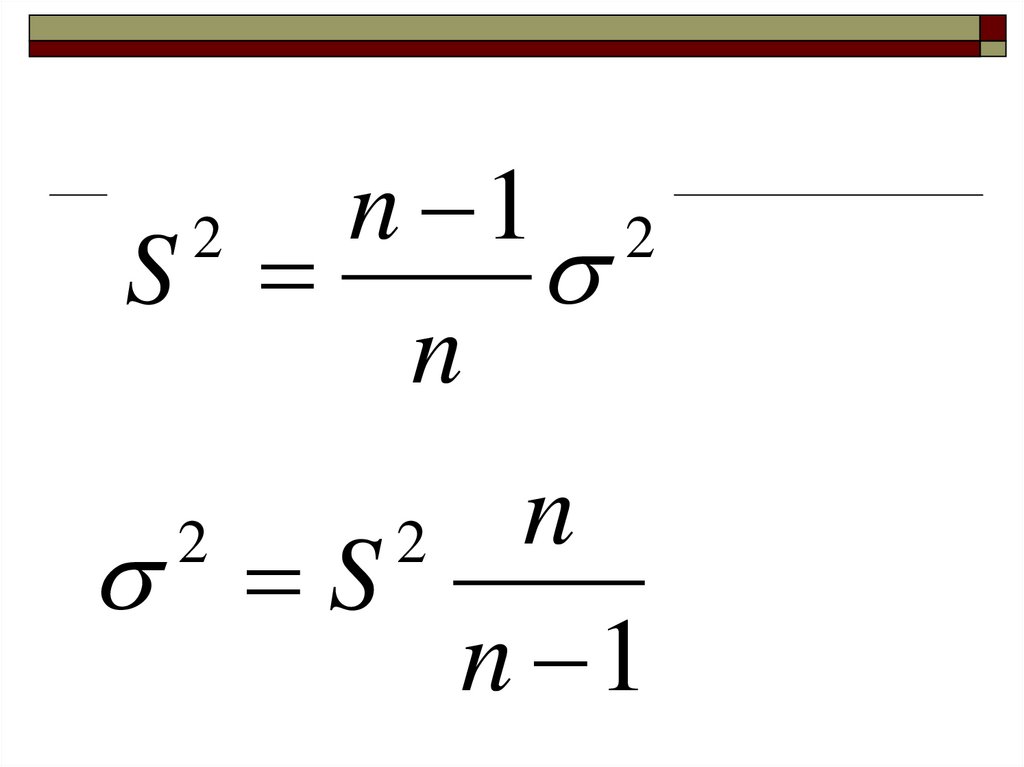
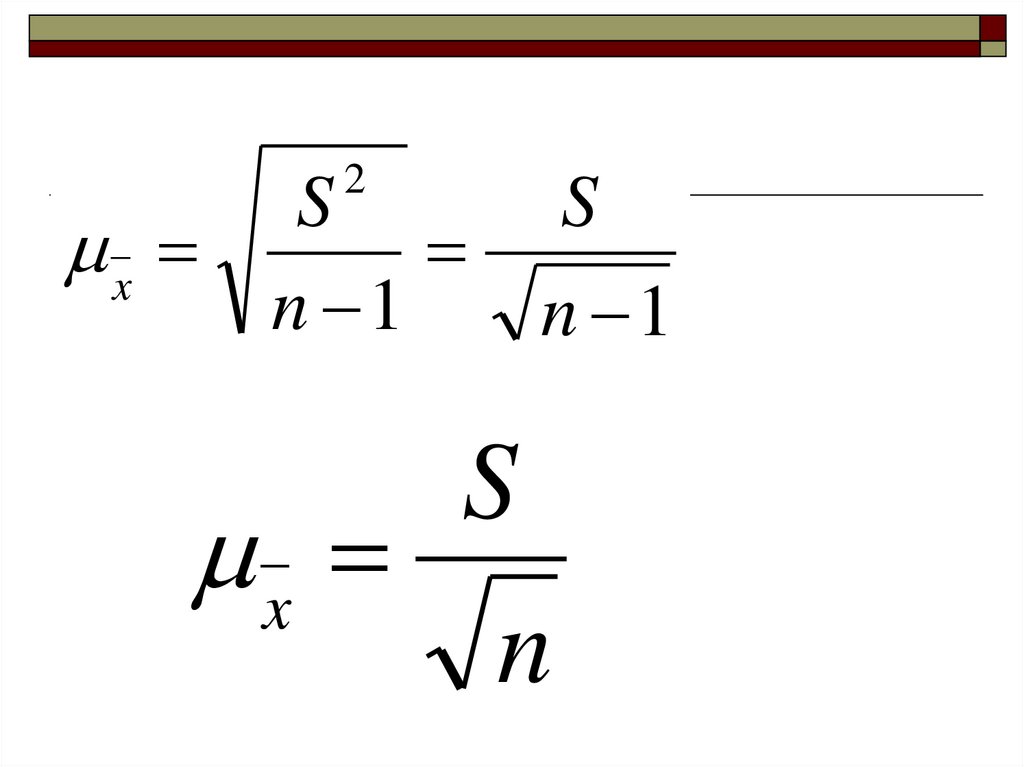
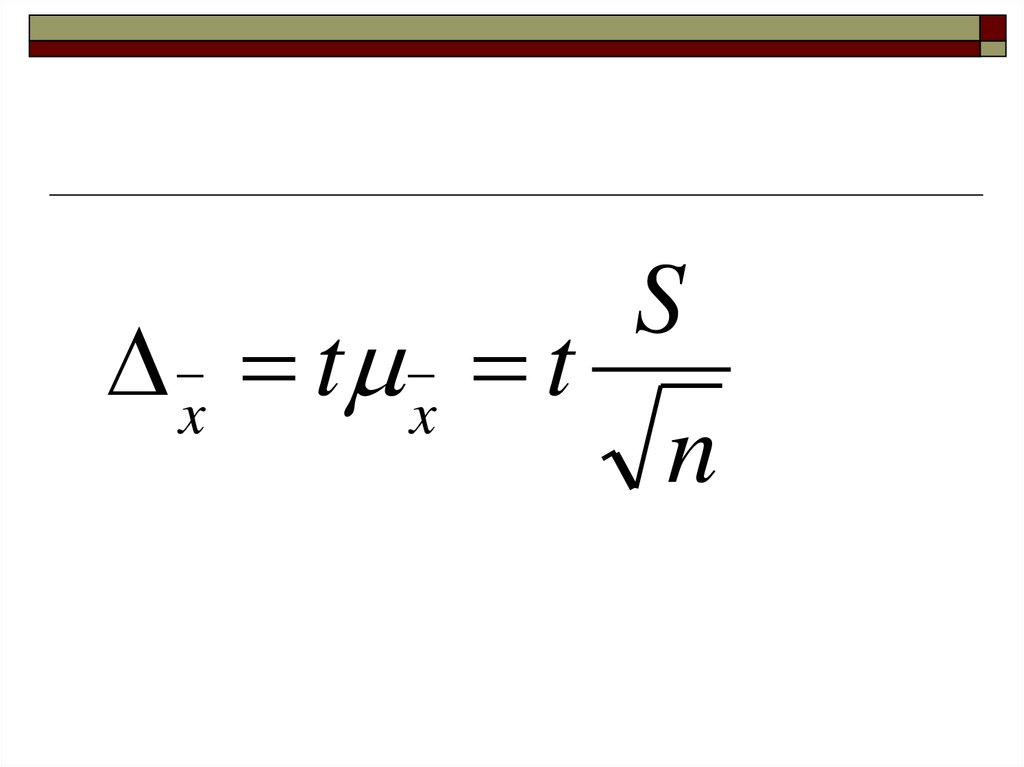
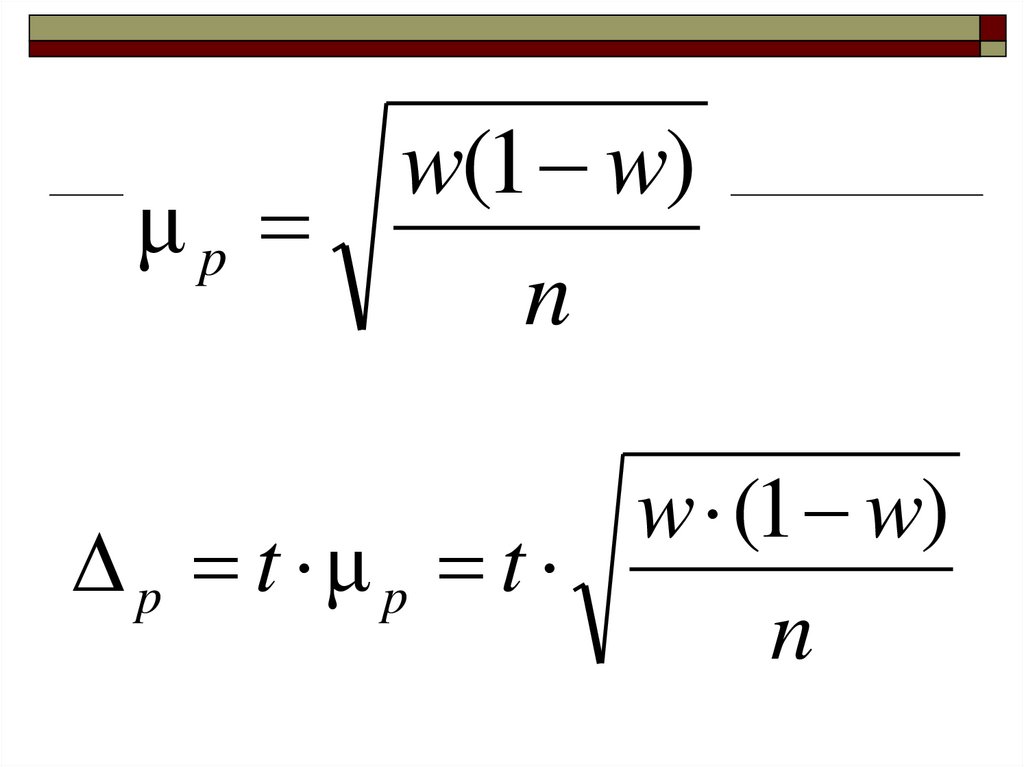

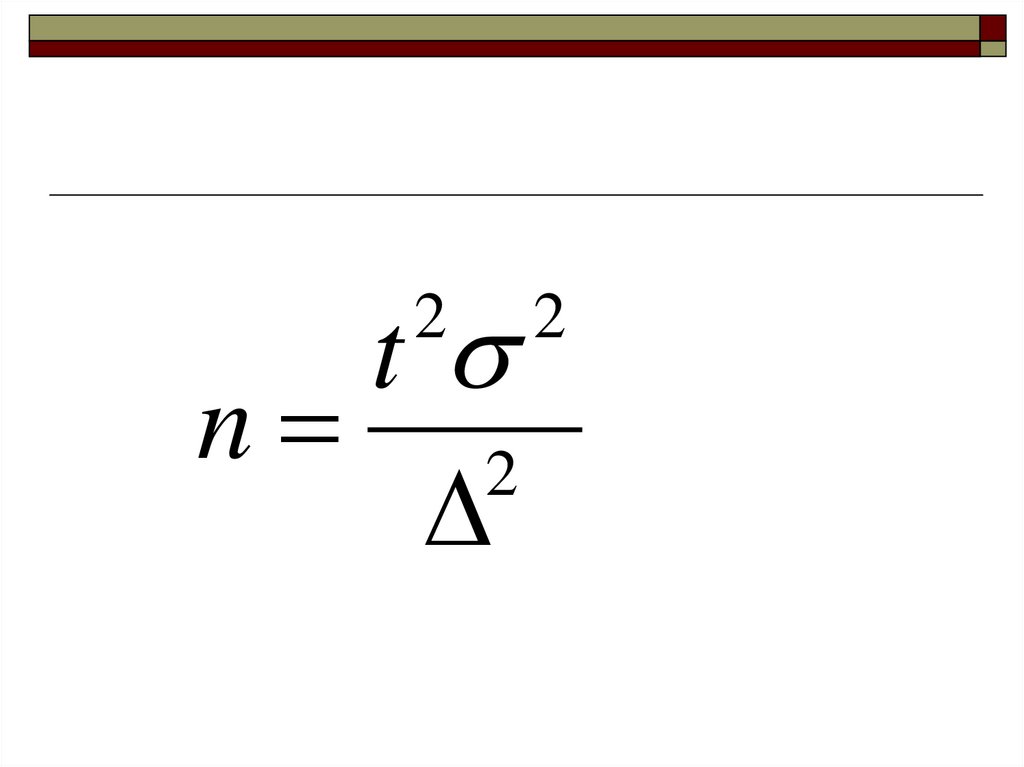
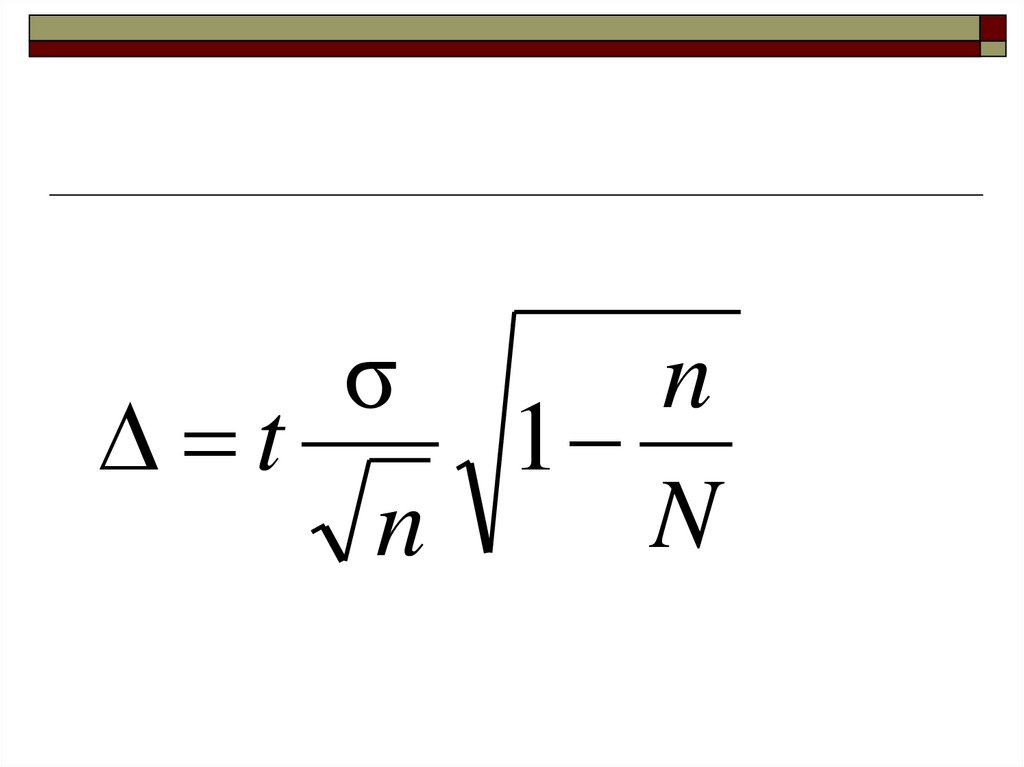
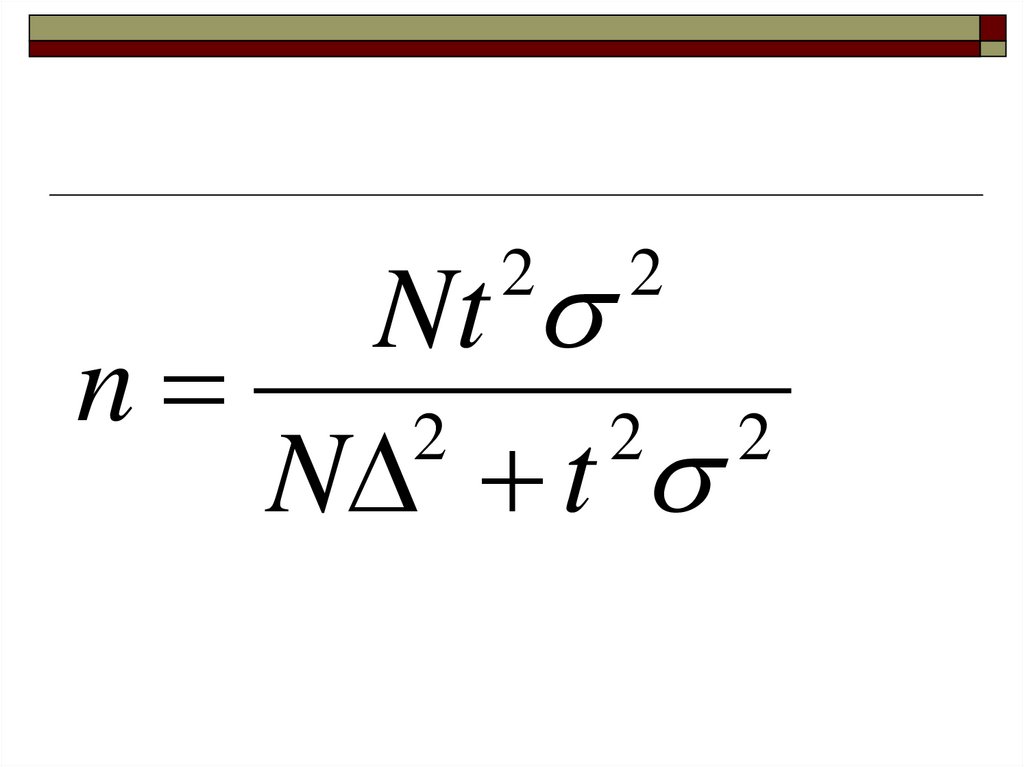
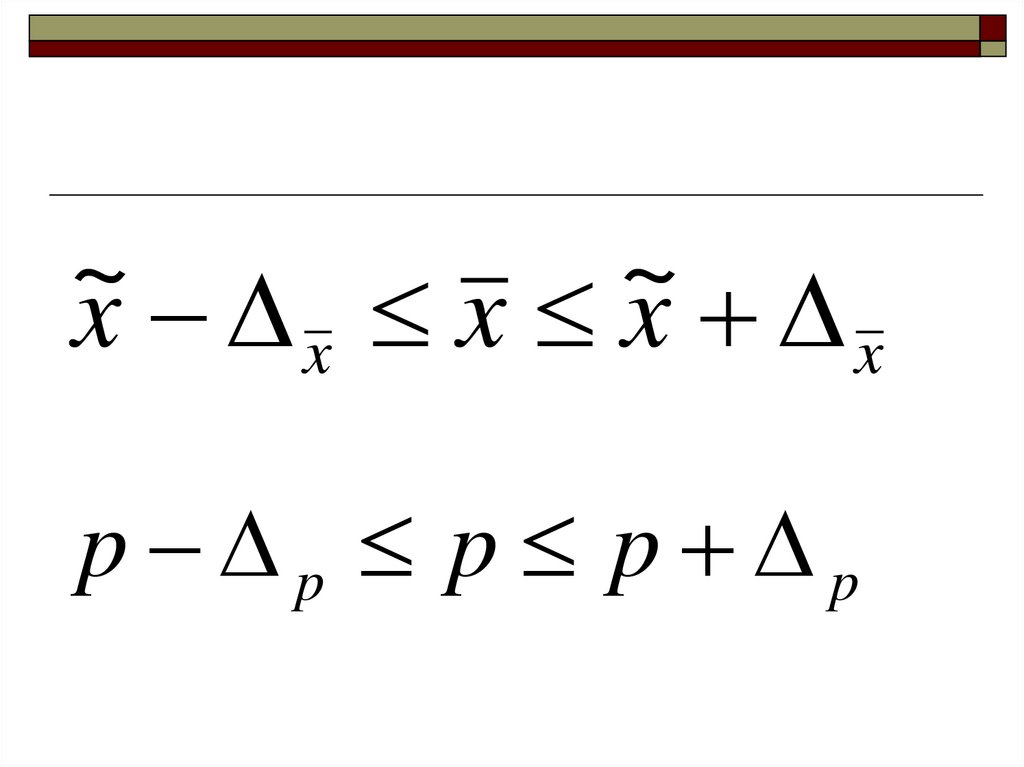

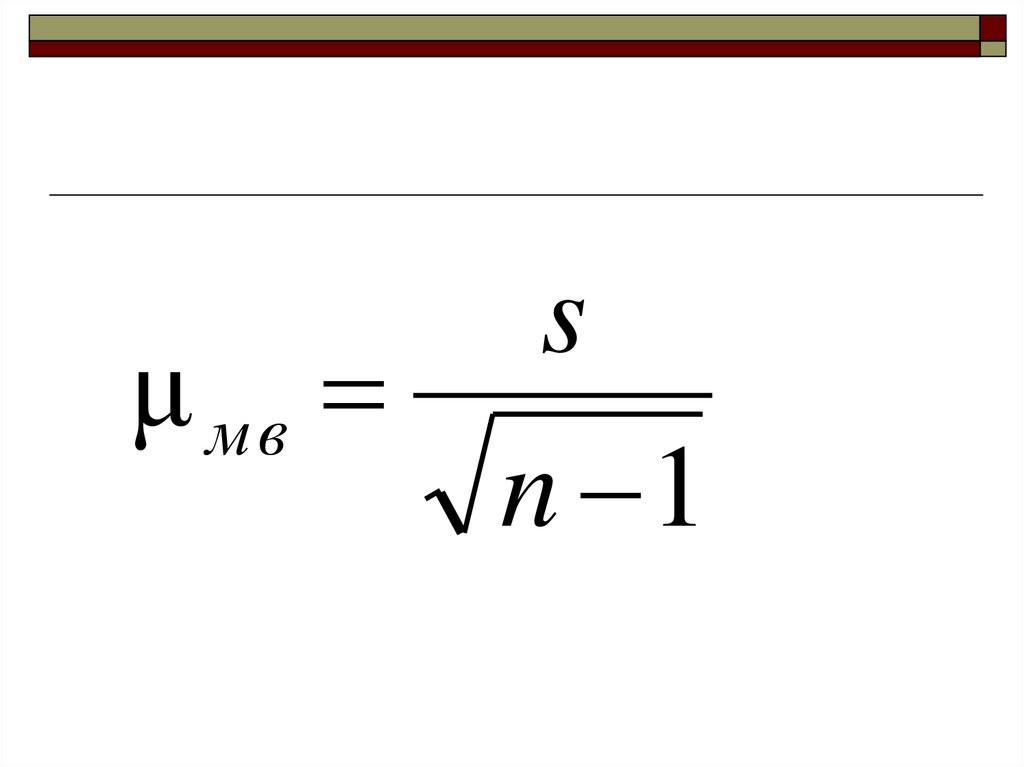

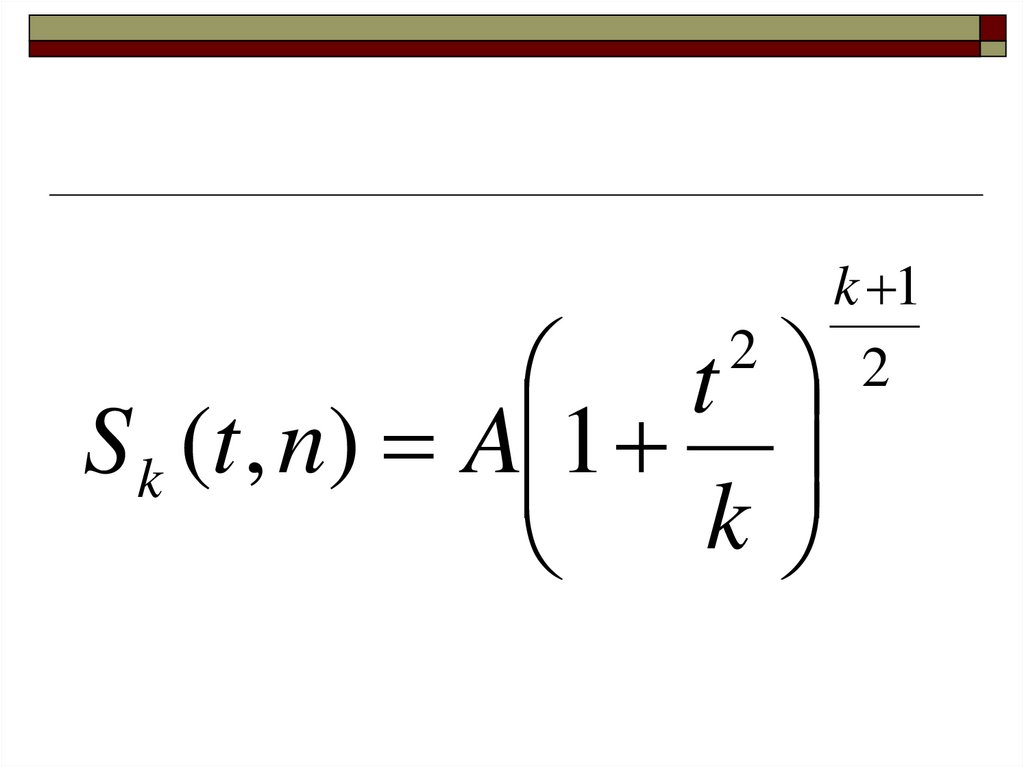

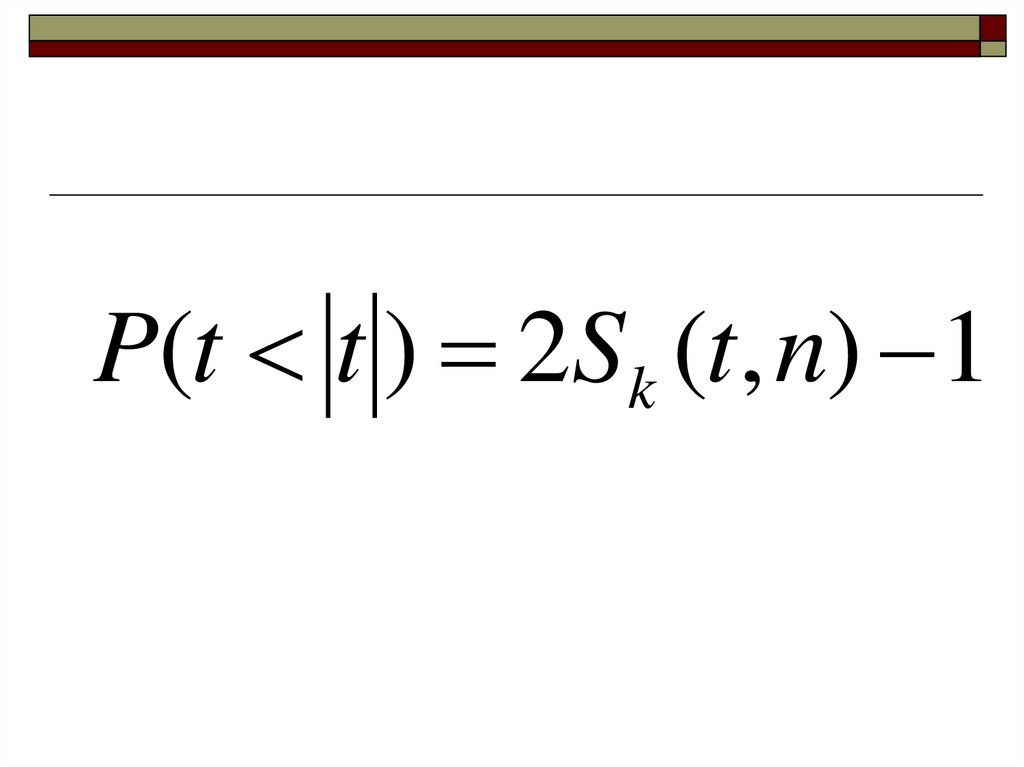
 mathematics
mathematics








