Представление числовой информации в ПК

1. Представление числовой информации в ПК

2. Представление числовой информации в ПК

Формат с
фиксированной
точкой:
1. Без знака
2. Со знаком
(только целые)
Формат с
плавающей
точкой
(вещественные)

3. Представление чисел в формате с фиксированной запятой без знака

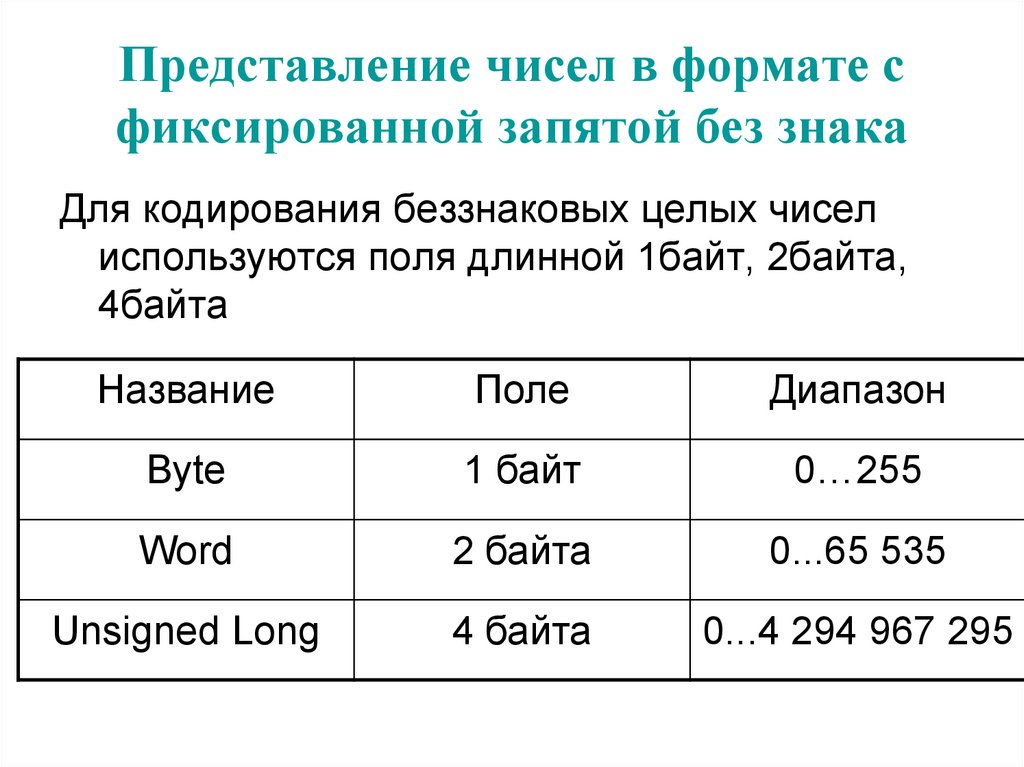
Для кодирования беззнаковых целых чисел
используются поля длинной 1байт, 2байта,
4байта
Название
Поле
Диапазон
Byte
1 байт
0…255
Word
2 байта
0...65 535
Unsigned Long
4 байта
0...4 294 967 295

4. Алгоритм записи чисел в формате с фиксированной запятой без знака

• Перевести исходное число в двоичную
систему счисления
• Поместить полученные цифры в
выбранное для кодирования поле

5. Пример 1. Получить внутреннее представление целого числа 1607 в 2-х байтовой ячейке.

Решение
1. N= 160710=110010001112
2. Внутреннее представление числа:
0000 0110 0100 0111
3. Шестнадцатеричная форма внутреннего
представления числа:
0647

6. Представление чисел в формате с фиксированной запятой со знаком

Название
Поле
Диапазон
Short
Integer
1 байт
-128…+127
Integer
2 байта
-32768...+32767
Long
Integer
4 байта
2147483648...+2147483647

7. Алгоритм записи кода целого числа со знаком:

1. Получаем двоичный код числа
2. Выбираем соответствующее поле для
кодирования
3. В старший бит выбранного поля записываем
знак числа (1- «-», 0- «+»), а остальные биты
справа налево помещаем в поле и дополняем
нулями до старшего бита

8. Пример 2. Получить внутреннее представление целого отрицательного числа -600 в 2-х байтовой ячейке.

Решение
1. N= -60010=-10010110002
2. Внутреннее представление числа:
1000 0010 0101 1000
3. Шестнадцатеричная форма
внутреннего представления числа:
8258

9. Алгоритм записи значения целого числа со знаком по его коду:

• Записать код числа в двоичной системе
счисления
• Отделить старший бит и записать знак
числа
• Оставшиеся биты дают модуль
искомого числа

10. Пример 3. Получить значение целого числа со знаком по его коду: 80А316

Решение
1. 80А316=1000 0000 1010 00112
2. Отделяем первый бит и записываем
знак «-»
3. По оставшемуся коду числа находим
его значение: 1010 00112 =16310
4. 80А316=-16310

11. Кодирование целых чисел со знаком с помощью комплиментарного кода

Рассмотрим пример:
Если выполнить обычное кодирование со
знаком и выполнить сложение двух
противоположных по знаку чисел, то
возникнет противоречие:
+410=0000 01002
-410=1000 01002
0000 01002+1000 01002=1000 10002
Система кодирования со знаком не
приемлема!!!

12. Алгоритм записи комплиментарного кода целых чисел со знаком:

1. Перевести модуль искомого числа в
двоичную систему счисления
2. Выбрать поле, длина которого гарантирует
возможность записи знакового кода
искомого числа
3. Если число «+», то записать полученный
двоичный код (прямой) в выбранное
поле(справа налево)
4. Если число «-», то в выбранное поле
необходимо записать дополнительный код,
который образуется по следующему
правилу:

13.

• Полученный прямой код инвертируется,
т.е. каждая цифра 0 заменяется на 1, а
1 на 0;
• Полученный таким образом обратный
код с дополнением 1 увеличиваем на 1;
• Полученный дополнительный код
записывается в выбранное поле.

14. Пример 3. Выполните кодирование чисел +77 и -77 с помощью комплиментарного кода и выполните действие сложения

Решение
1. +7710=10011012
2. SI: 0100 11012 = 4D16
3. -7710=-10011012
4. SI: 010011012=101100102
5. 101100102 + 000000012= 101100112
6. 101100112=B316
7. 010011012+101100112=1 000000002

15. Получение значения числа по его комплиментарному коду

1. По знаковому биту определить знак числа,
если число «+», то оставшиеся биты дают
прямой код значения числа
2. Если число «-», то в исходном поле
получают дополнительный код из которого
по формуле:
p= M(база)-α(доп.код)
Вычисляют модуль искомого числа
3. Полученный прямой код в виде двоичной
системы счисления необходимо перевести
в десятичную
4. Приписав знак числа получить искомое число

16. Пример 4.Найти значение числа по его комплиментарному коду FFE816

• FFE816=отрицательное число
• Т.к. поле двухбайтовое, то база=1000016
(в однобайтовом=10016, в
четырехбайтовом=10000000016)
1000016-FFE816=001816
• 1816=2410
• FFE816=2410

17. Достоинства представления чисел в формате с фиксированной точкой

• Простота
• Наглядность представления чисел
• Простота алгоритмов реализации
арифметических операций
Недостатки представления чисел в
формате с фиксированной точкой
• небольшой диапазон представления
величин, недостаточный для решения
математических, экономических и др. задач.

18. Представление чисел в формате с плавающей запятой

• Базируется на экспоненциальной форме записи числа:
A = ±m *q±n
m - мантисса числа
Q – основание СС
N – порядок числа
• Пример. Преобразуйте число +555,55, записанное в
естественной форме, в экспоненциальную форму с
нормализованной мантиссой: +555,55 =+0,55555 * 103
Нормализованная мантисса: +0,55555
Порядок: n = 3

19. Алгоритм записи вещественного числа в четырехбайтовое поле:

Перевести модуль числа в двоичную СС
Нормализовать двоичное число
Записать код знака числа
Записать истинный порядок числа (ри)
Найти машинный порядок в двоичной СС:
рм=ри + 2 к-1
6. Заполнить поле мантиссы слева направо,
отбрасывая бит целой части и дополняя
оставшиеся поля мантиссы нулями
7. Полученное заполненное поле записать в 16-ой
СС
1.
2.
3.
4.
5.

20. Пример 1 . Записать внутреннее представление числа 250,1875 в форме с плавающей точкой. Решение

1.
Переведем в двоичную СС:
250,187510=11111010, 00110000000000002
2.
Запишем в форме нормализованного двоичного числа:
0, 11111010 0011000000000000 * 1021000
(мантисса, основание СС 210=102 и порядок 810=10002)
3. Вычислим машинный порядок в двоичной СС:
Мp2 = 1000 +1000000 = 100 1000
3. Запишем число в 4-х байтовой ячейке:
0
1001000
1111 1010 0011 0000 0000 0000
Шестнадцатеричная форма 48FА3000

21. Алгоритм получения числа по его коду в формате с плавающей запятой:

• Перевести исходный код в двоичную СС
• Выделить код знака и определить знак числа
• Выделить код машинного порядка
• Получить истинный код: ри=рм-2к-1
• Выделить мантиссу и добавить в целую часть
1
• Записать число в нормализованном виде
• Записать денормализованное число
• Перевести в 10ю СС

22. Пример 2 . По шестнадцатеричной форме внутреннего представления числа в форме с плавающей точкой CC98811000 восстановить число.

Решение
1. Перейдем к двоичному представлению числа:
1100 1001 1000 0001 0001 0000 0000 0000
1
31
1001001
10000001
00010000
00000000
23
0
2. В старшем разряде с номером 31 записана 1, значит получен код
отрицательного числа. Получим порядок числа:
p=10010012 – 1000002=10012=910
3. Запишем в виде нормализованного дв. числа с плавающей точкой с
учетом знака числа: -0,100000010001000000000000·21001
4. В двоичной системе СС число имеет вид: -100000010,0012
5. Переведем число в десятичную СС:
-100000010,0012=-(1*28+1*21+1*2-3)=-258,12510