Представление чисел в компьютере

1. Представление чисел в компьютере

МАОУ «Лицея №36»
Заблоцкая Инна Александровна

2. Целые числа без знака, под которые отводится 1 байт

Под значение числа отводятся все разряды в байте
7
byte:
6
5
4
3
2
1
0
0 0 0 0 0 0 0 0 =0
0 0 0 0 1 0 0 1 =9
1 1 1 1 1 1 1 1 =255

3. Целые числа без знака, хранящиеся в 2 байтах

Под значение числа отводятся все разряды в слове
word:
15 14 13 12 11 10 9
8
7
6
5
4
3
2
1
0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 =0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 =4
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 =65535

4. Представление целых чисел со знаком

Прямой код
Дополнительный код

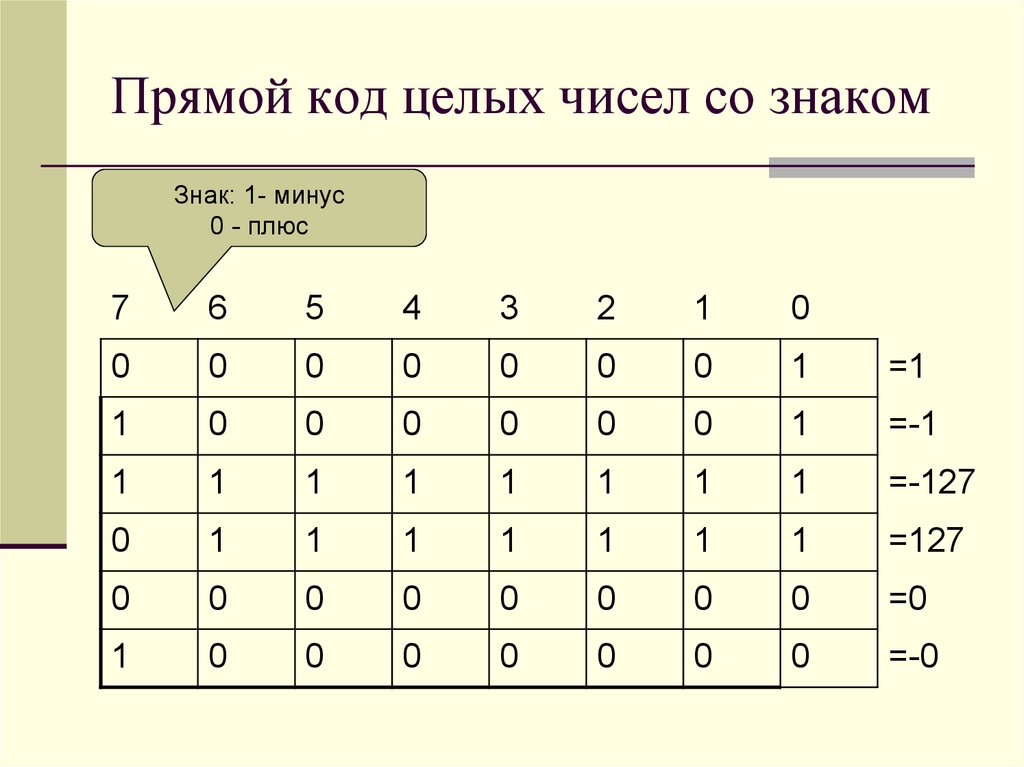
5. Прямой код целых чисел со знаком

Знак: 1- минус
0 - плюс
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
1
=1
1
0
0
0
0
0
0
1
=-1
1
1
1
1
1
1
1
1
=-127
0
1
1
1
1
1
1
1
=127
0
0
0
0
0
0
0
0
=0
1
0
0
0
0
0
0
0
=-0

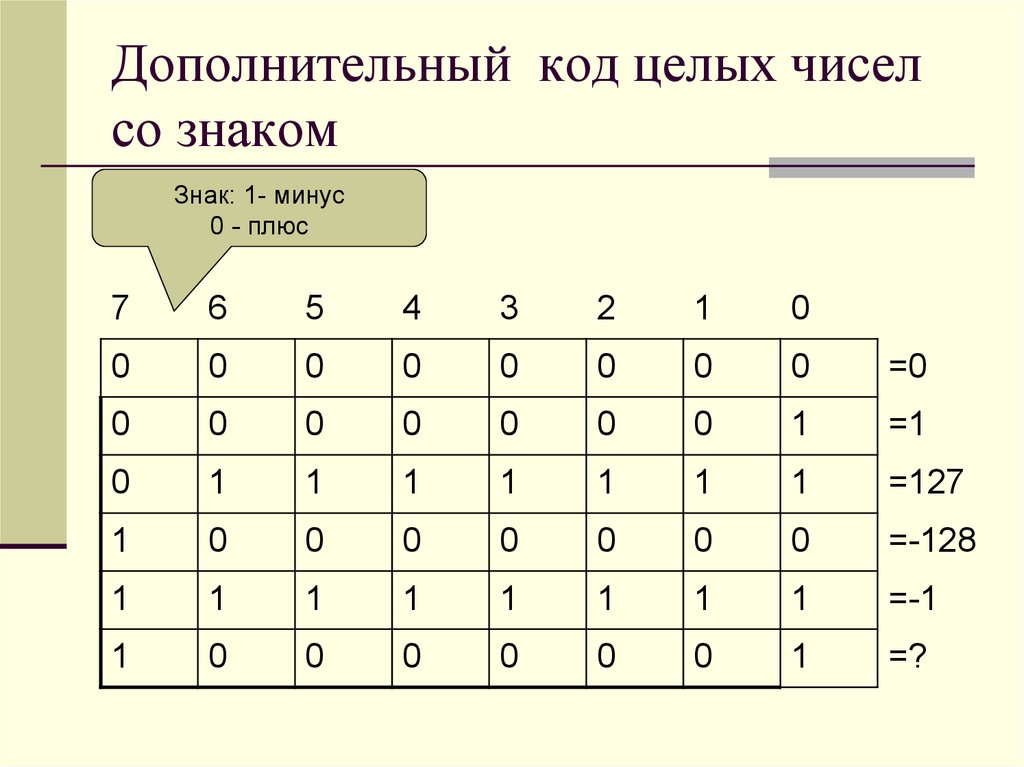
6. Дополнительный код целых чисел со знаком

Знак: 1- минус
0 - плюс
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
=0
0
0
0
0
0
0
0
1
=1
0
1
1
1
1
1
1
1
=127
1
0
0
0
0
0
0
0
=-128
1
1
1
1
1
1
1
1
=-1
1
0
0
0
0
0
0
1
=?

7. Дополнительный код положительного числа

Дополнительный код положительного
числа равен прямому коду
положительного числа.
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
=0
0
0
0
0
0
0
0
1
=1
0
1
1
1
1
1
1
1
=127

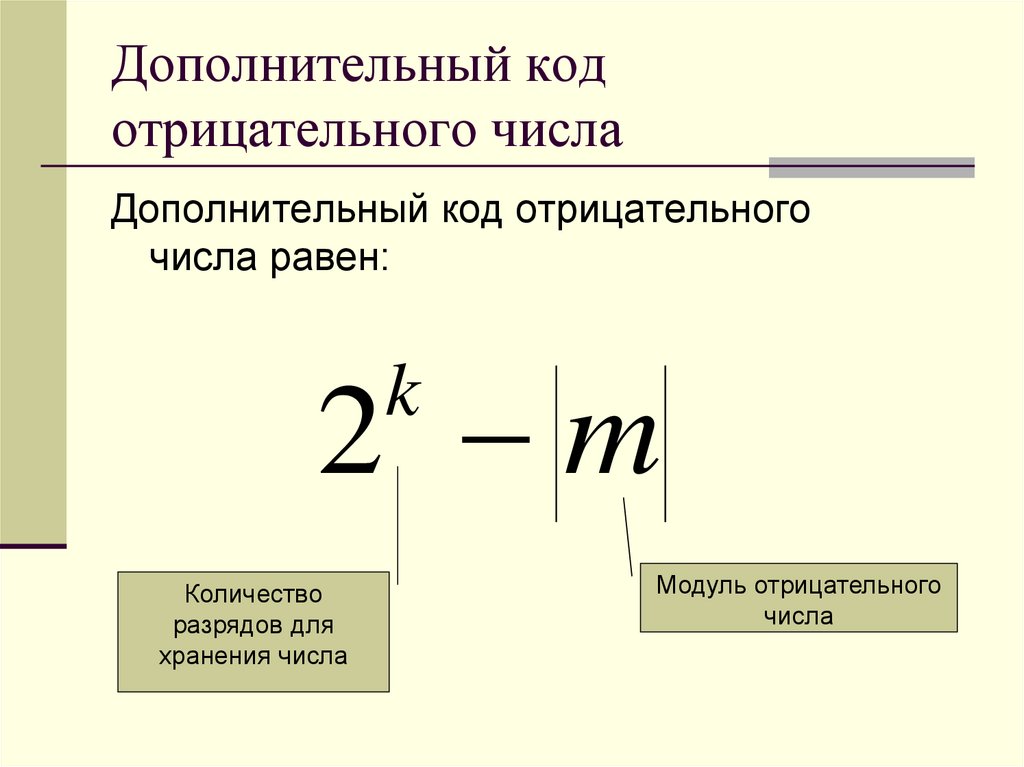
8. Дополнительный код отрицательного числа

Дополнительный код отрицательного
числа равен:
2 m
k
Количество
разрядов для
хранения числа
Модуль отрицательного
числа

9. Определение дополнительного кода отрицательного числа -5

Перевести модуль числа в двоичную систему
счисления: 510=1012.
2. Вписать число в заданное количество
разрядов:
1.
15 14 13 12 11 10 9
8
7
6
5
4
3
2
1
0
0
0
0
0
0
1
0
1
7
6
5
4
3
2
1
0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1

10.

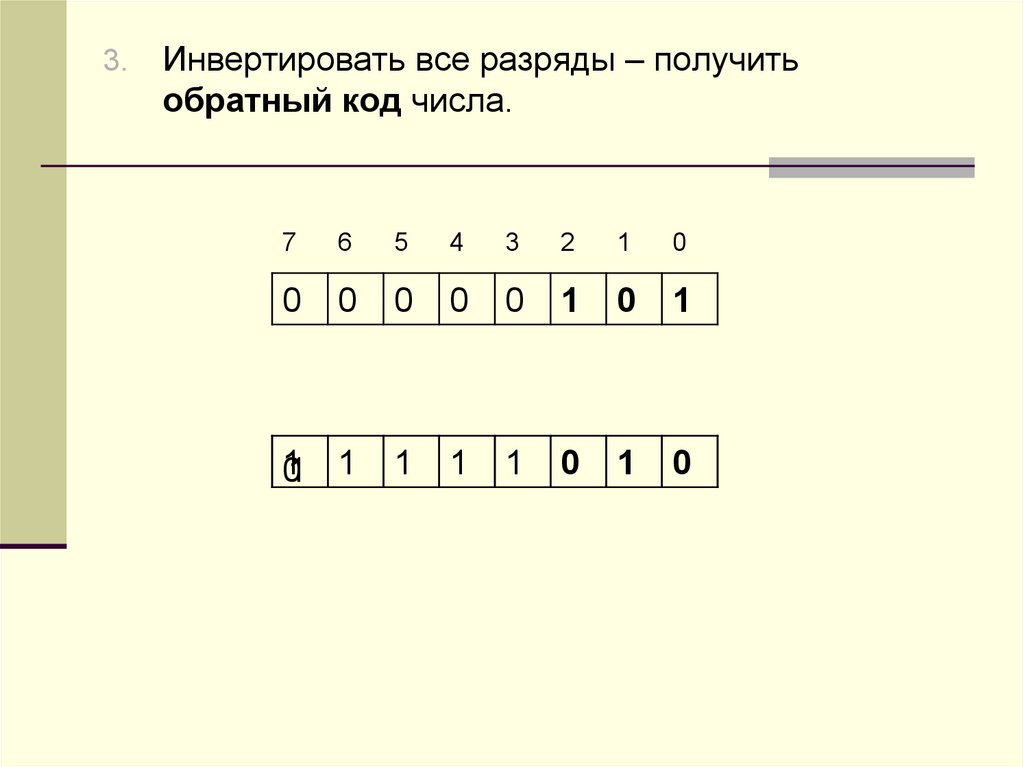
3.
Инвертировать все разряды – получить
обратный код числа.
7
6
5
4
3
2
1
0
0
0
0
0
0
1
0
1
1
01 1
1
1
1
0
1
0

11.

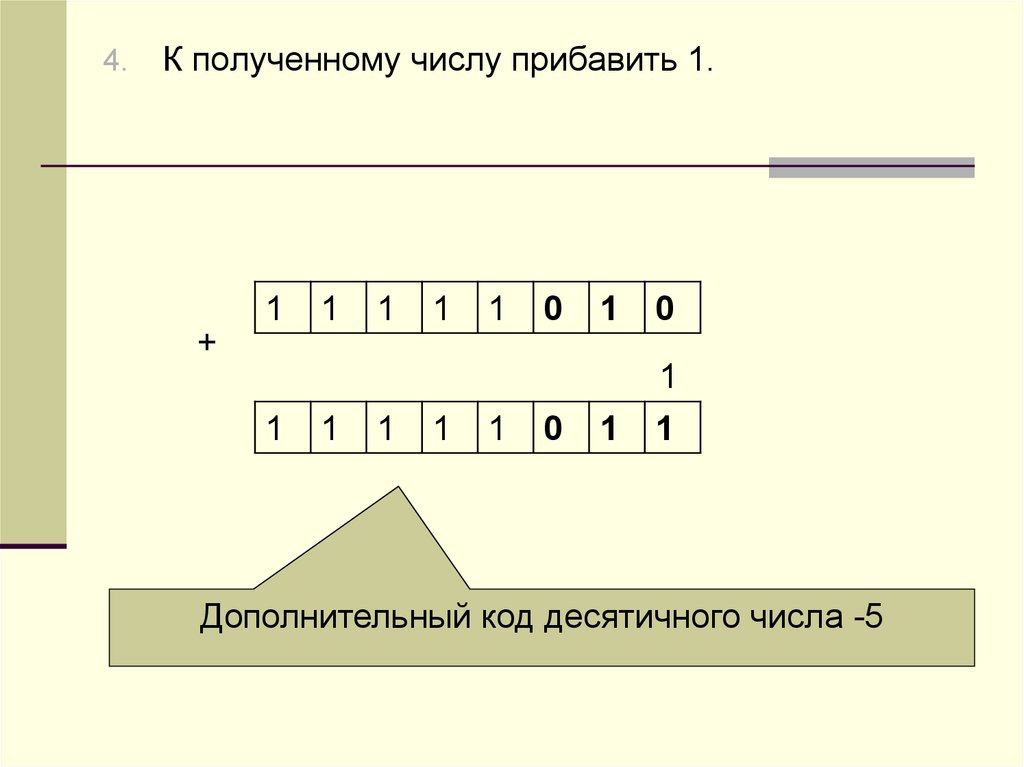
4.
К полученному числу прибавить 1.
1
1
1
1
1
0
1
0
+
1
1
1
1
1
1
0
1
1
Дополнительный код десятичного числа -5

12. Получить дополнительный код числа -5 для шестнадцатиразрядной ячейки

15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
0
+
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
1

13. Самостоятельная работа

1.
Получите прямые коды байтового
представления следующих десятичных чисел:
1.
2.
3.
2.
-12
25
-126
Получите дополнительные коды байтового
представления следующих десятичных чисел:
1.
2.
3.
-12
25
-126

14. Получение значения целого отрицательного числа по дополнительному коду

1. Из дополнительного числа вычесть 1.
2. Инвертировать полученный код.
3. Перевести полученный код в десятичную
систему счисления.
4. Перед полученным числом поставить
знак
-.

15. Пример 1:

Определить десятичный эквивалент знакового
числа, которое хранится в байте:
0 1 1 1 1 0 1 0
Решение.
1. Число положительное, т.к. знаковый разряд содержит 0.
2. Переведем его в восьмеричную систему счисления: 1728,
или шестнадцатеричную систему: 7А16.
3. Переведем его в десятичную систему:
1*8*8+7*8+2=64+56+2=12210 или 7*16+10=112+10=12210.
Ответ: Десятичный эквивалент знакового байтового числа
111010 равен 122.

16. Пример 2:

Определить десятичный эквивалент знакового
числа, которое хранится в байте:
1 1 1 1 1 0 1 0
Решение.
1. Число отрицательное, т.к. знаковый разряд содержит 1.
2. Вычитаем из него 1 и инвертируем:
1 1 1 1 1 0 1 0
1
1 1 1 1 1 0 0 1
0 0 0 0 0 1 1 0

17. Пример 2:

0 0 0 0 0 1 1 0
Решение.
3. Переведем его в восьмеричную систему счисления: 68,
или шестнадцатеричную систему: 616.
4. Переведем его в десятичную систему:
68=610 или 616=610.
5. Не забудем, что число отрицательное.
Ответ: десятичный эквивалент знакового байтового
числа 1111010 равен -6.

18. Задача 2.34

Переменные Х, Х1, Х2 и Х3 имеют размер
байт, тип – знаковый.
В шестнадцатеричной системе счисления
Х1=DA16, X2=EB16, X3=А716. Значение
выражения Х=(Х1-Х2)*Х3 в десятичной
систем счисления равно _____.

19. Решение задачи 2.34

1.
Переведем исходные числа в байтовое
представление двоичной системы счисления:
Х1:
1
1
0
1
1
0
1
0
Х2:
1
1
1
0
1
0
1
1
Х3:
1
0
1
0
0
1
1
1

20. Операция вычитания в компьютере реализуется путем сложения с дополнительным кодом.

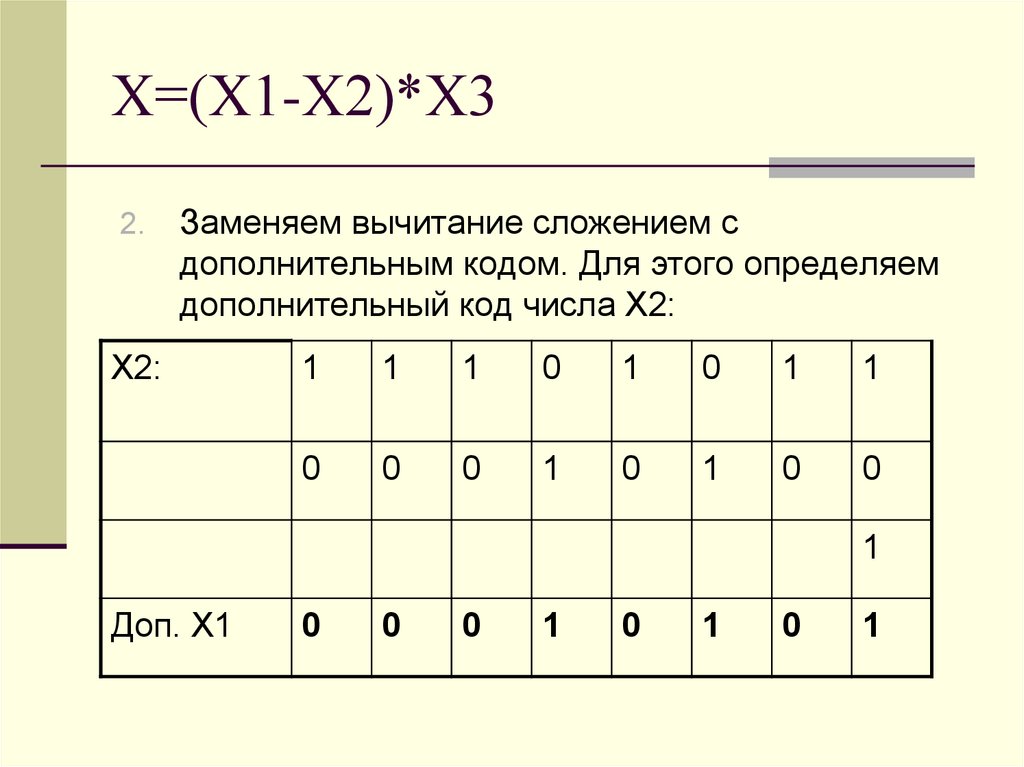
21. Х=(Х1-Х2)*Х3

2.
Заменяем вычитание сложением с
дополнительным кодом. Для этого определяем
дополнительный код числа Х2:
Х2:
1
1
1
0
1
0
1
1
0
0
0
1
0
1
0
0
1
Доп. Х1
0
0
0
1
0
1
0
1

22. Х=(Х1+ доп.Х2)*Х3

Х1:
1
1
0
1
1
0
1
0
Доп. Х2:
0
0
0
1
0
1
0
1
Х1+доп.
Х2:
1
1
1
0
1
1
1
1

23. Х=(Х1+ доп.Х2)*Х3

Х1+доп. Х2:
Х3
1
0
1
0
0
1
0
0
1
0
0
1
0
0
0
0
1
1
0
1
1
1
1
0
0
1
0
1
1
1
1
1
1
0
0
1
0
1
1
1
0
1
1
0
0
0
1
0
1
1
1
0
1
0
0
1
0
0
0
1
1
0
0
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
0
0
1

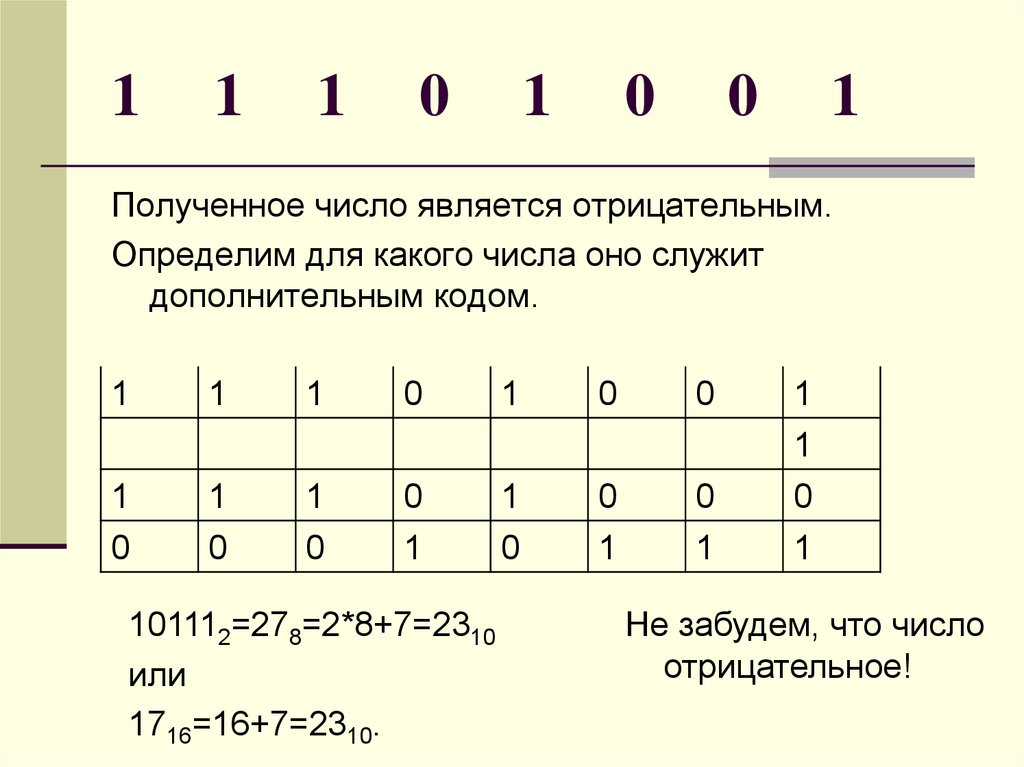
24. 1 1 1 0 1 0 0 1

Полученное число является отрицательным.
Определим для какого числа оно служит
дополнительным кодом.
1
1
1
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
1
0
1
101112=278=2*8+7=2310
или
1716=16+7=2310.
1
1
0
1
Не забудем, что число
отрицательное!

25. Ответ к задаче 2.34

Переменные Х, Х1, Х2 и Х3 имеют размер байт, тип
– знаковый.
В шестнадцатеричной системе счисления
Х1=DA16, X2=EB16, X3=А716.
Значение выражения Х=(Х1-Х2)*Х3 в десятичной
систем счисления равно -23.

26. Представление вещественных чисел

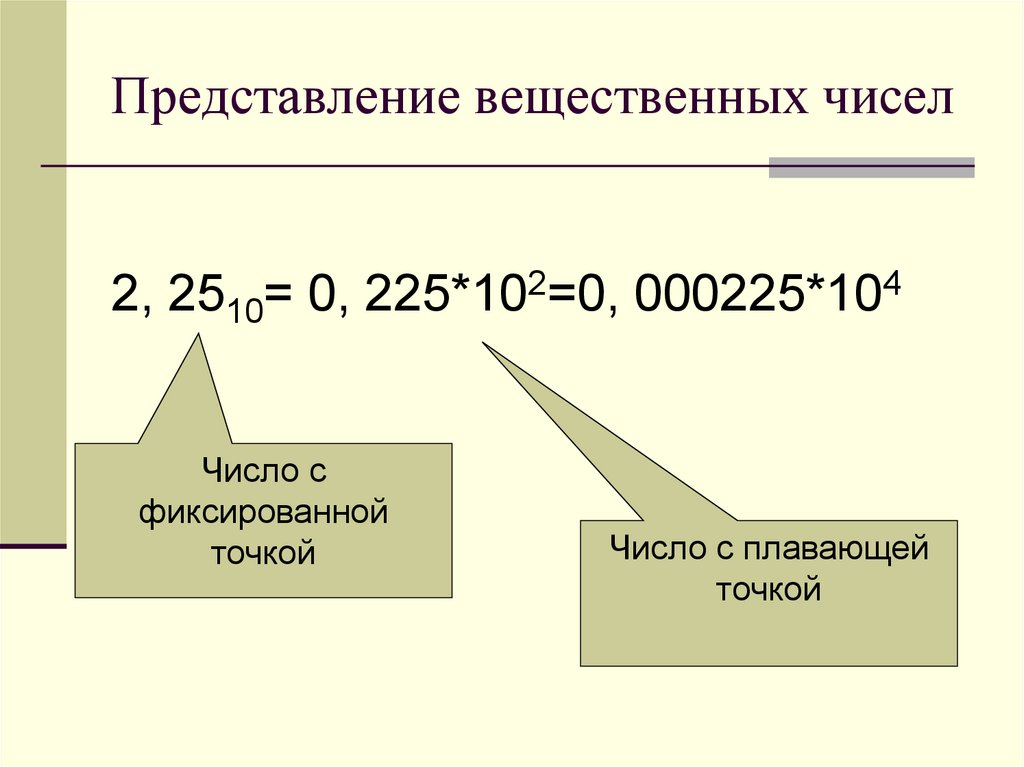
27. Представление вещественных чисел

2, 2510= 0, 225*102=0, 000225*104
Число с
фиксированной
точкой
Число с плавающей
точкой

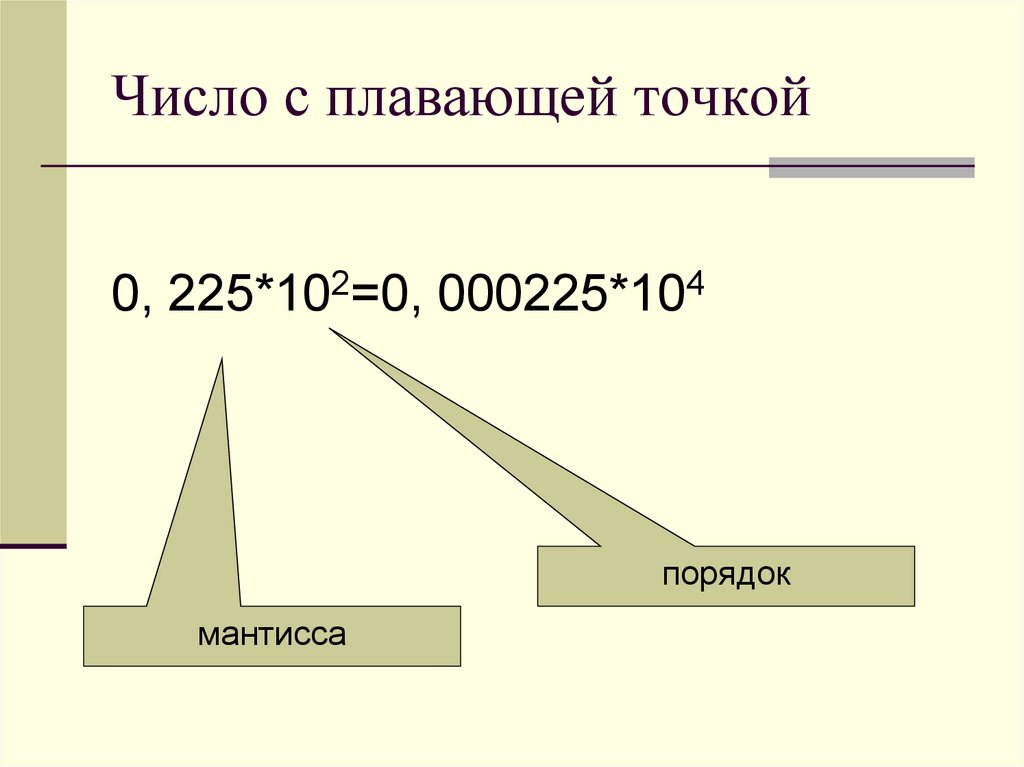
28. Число с плавающей точкой

0, 225*102=0, 000225*104
порядок
мантисса

29. Общий вид числа с плавающей точкой

A m p
n
m – мантисса
p – основание системы
счисления
n - порядок

30. Например:

1.
0, 0234*56
2.
0, 0234*96
3.
2,34*56
4.
0, 0234*166
A m p
n
m – мантисса
p – основание
системы
счисления
n - порядок

31. Нормализованные числа с плавающей запятой

Число называется нормализованным,
если:
1 m 1
p
0,123*102 – нормализованное число
0,0123*103 –
1,23*101 –
123,0*10-1

32. Вещественный тип single

Величины типа single занимают в памяти 4
байта, т.е. 32 бита.
разряды
31
30..23
1 бит 8 бит
22..0
23 бита
значения
Знак Порядок
числа
мантисса
Мантисса определяет точность представления числа.
Порядок определяет диапазон подставляемых чисел.

33. Знак числа

0 – число положительное
1 – число отрицательное

34. Порядок

Истинный порядок = порядок -127
0
0
0
0
0
0
0
0
Истинный порядок = 0 -127=-127
1
1
1
1
1
1
Истинный порядок = 255 -127=128
1
1

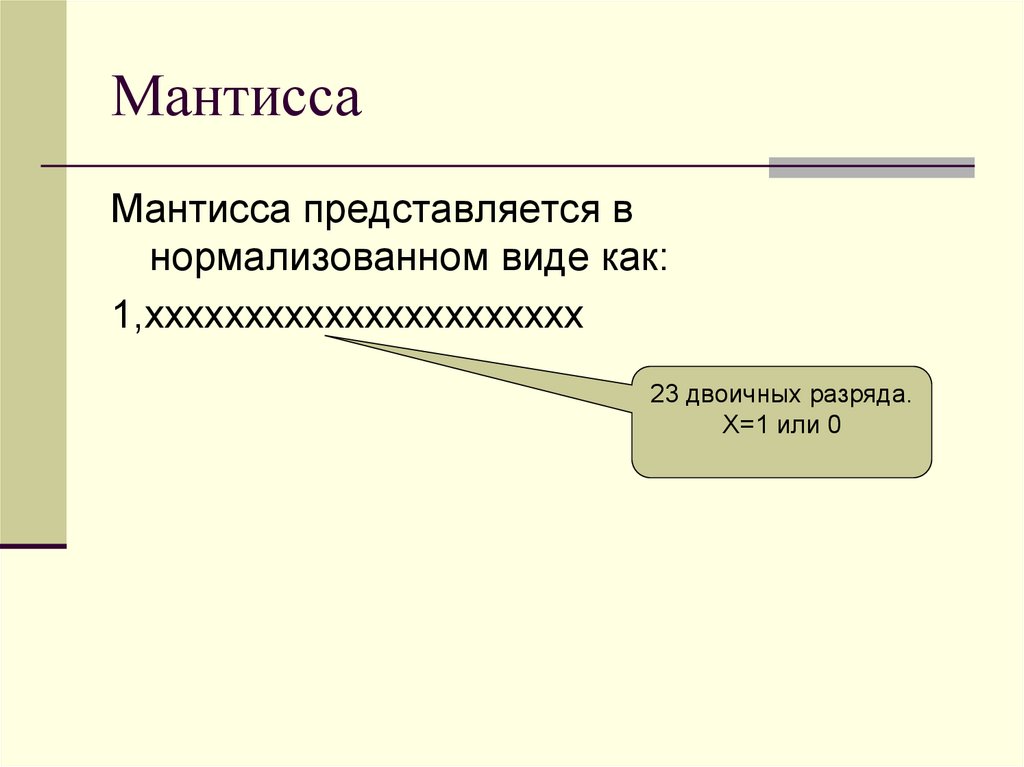
35. Мантисса

Мантисса представляется в
нормализованном виде как:
1,хххххххххххххххххххххх
23 двоичных разряда.
Х=1 или 0

36. Задача 2.35

Значение переменной А представлено в
форме с плавающей точкой в
шестнадцатеричной системе счисления
А=C286000016. Тип переменной A – single
для языков BASIC и PASCAL. Десятичное
значение числа А равно ____.

37. Решение задачи 2.35

1.
2.
3.
4.
5.
6.
7.
Запишем двоичный код числа А=C2860000:
1100 0010 1000 0110 0000 0000 0000
Число отрицательное.
Порядок равен: 10000101=2058=2*64+5=13310
Истинный порядок равен 133-127=6.
Мантисса равна:1, 0000110000000000000
Записать число, учитывая истинный порядок:
1, 0000110000000000000*26=
1000011,0000000000000= 1038=64+3=6710
Записать ответ с учетом знака: -67

38. Задача 2.183

Значение переменной А представлено в
форме с плавающей точкой в
шестнадцатеричной системе счисления
A=43610000. Тип переменной А single для
языков BASIC и PASCAL. Десятичное
значение числа А равно ___.

39. Решение задачи 2.183

1. А=4361000016=
0100 0011 0110 0001 0000 0000 0000 0000
2. Число положительное.
3. Порядок=10000110=2068=2*64+6=13410.
4. Истинный порядок= 134-127=7.
5. Мантисса равна:
1,110 0001 0000 0000 0000 0000.
6. Число, с учетом порядка, равно:
1,1100001*27=111000012=3418=3*64+4*8+1=22510
Ответ с учетом знака: 225.

40. Задача 2.184

А=С3570000
Ответ: -215

41. Решение задачи 2.184

А=С3570000
1. 1100 0011 0101 0111 0000 0000 0000 0000
2. Число отрицательное.
3. 10 000 110=2068=128+6=13410
4. Истинный порядок=134-127=7
5. Мантисса:
1,101 0111 0000 0000 0000 0000
6. Число, с учетом порядка,=
1,101 0111 0000 0000 0000 0000+27
=11 010 111=3278=3*64+2*8+7=21510
7. Запишем ответ с учетом знака
Ответ: -215

42. Задача 2.185

А=C2F20000
ОТВЕТ: -121

43. Задача 2.185

А=C2F20000
1. 1100 0010 1111 0010 0000 0000 0000 0000
2. Число отрицательное.
3. 1000 0101=8516=8*16+5=13310
4. Истинный порядок=133-127=6
5. Мантисса равна:
1,111 0010 0000 0000 0000 0000
6. Число, с учетом порядка, =
1,111 0010 0000 0000 0000 0000*26 =111 1001=
7916=7*16+9=12110
7. Ответ с учетом знака = -121.