Similar presentations:
Представление чисел в памяти компьютера. Тема 12
1. Тема 12: Представление чисел в памяти компьютера
2.
1. Что такое система счисления?2. Что такое основание системы
счисления?
3. Какие системы счисления используются
в ПК?
4. Какой алфавит и основание имеет
двоичная система счисления?
5. Какой алфавит и основание имеет
десятичная система счисления?
3.
Система счисления (англ. numeral system или system ofnumeration) — символический метод записи чисел,
представление чисел с помощью письменных знаков.
Основание системы счисления — количество различных
цифр, используемых в этой системе.
Позиционная система счисления — система счисления,
в которой значение каждого числового знака (цифры) в
записи числа зависит от его позиции (разряда).
Десятичная система счисления —
позиционная система счисления по целочисленному
основанию 10.
В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0,
называемые арабскими цифрами.
4.
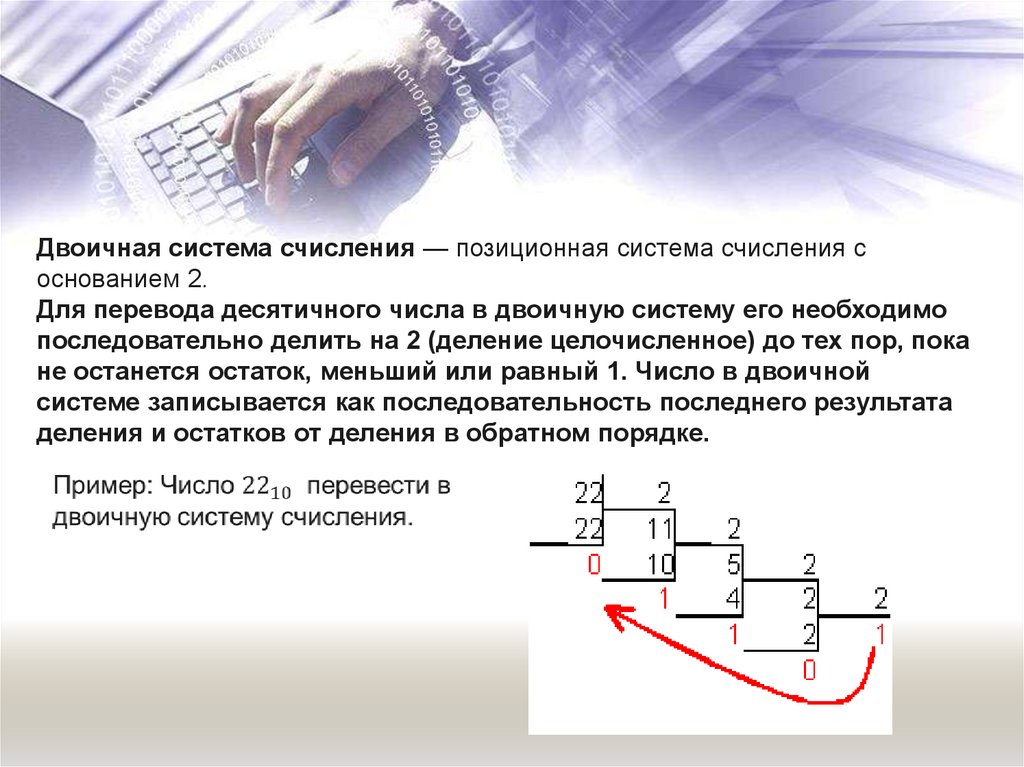
Двоичная система счисления — позиционная система счисления соснованием 2.
Для перевода десятичного числа в двоичную систему его необходимо
последовательно делить на 2 (деление целочисленное) до тех пор, пока
не останется остаток, меньший или равный 1. Число в двоичной
системе записывается как последовательность последнего результата
деления и остатков от деления в обратном порядке.
5.
Для перевода двоичного числа в десятичное необходимо его записать ввиде многочлена, состоящего из произведений цифр числа и
соответствующей степени числа 2, и вычислить по правилам десятичной
арифметики:
6.
7. Образ компьютерной памяти
8. Главные правила представления данных в компьютере:
Правило 1. Данные (и программы) впамяти компьютера хранятся в двоичном
виде, т. е. в виде цепочек единиц и нулей.
Правило 2. Представление данных в
компьютере дискретно.
Правило 3. Множество представимых в
памяти компьютера величин ограничено и
конечно.
Правило 4. В памяти компьютера числа
хранятся в двоичной системе счисления.
9. Правило 1
Данные (и программы) в памятикомпьютера хранятся в двоичном виде,
т. е. в виде цепочек единиц и нулей.
ПК может хранить и
обрабатывать
данные,
представляющие
информацию 4 видов:
числовую, текстовую,
графическую,
звуковую
10. Правило 2
Представление данных в компьютере дискретно.Дискретное множество состоит из отделенных друг от
друга элементов.
Самым традиционным видом данных, с которым
работает компьютер, являются числа.
Первоначально человек оперировал лишь целыми
положительными (натуральными) числами.
Натуральный ряд – дискретное множество чисел.
В математике натуральный ряд чисел бесконечен и
неограничен.
11. С появлением понятия отрицательного числа, оказалось, что множество целых чисел не ограниченно как «справа», так и «слева»
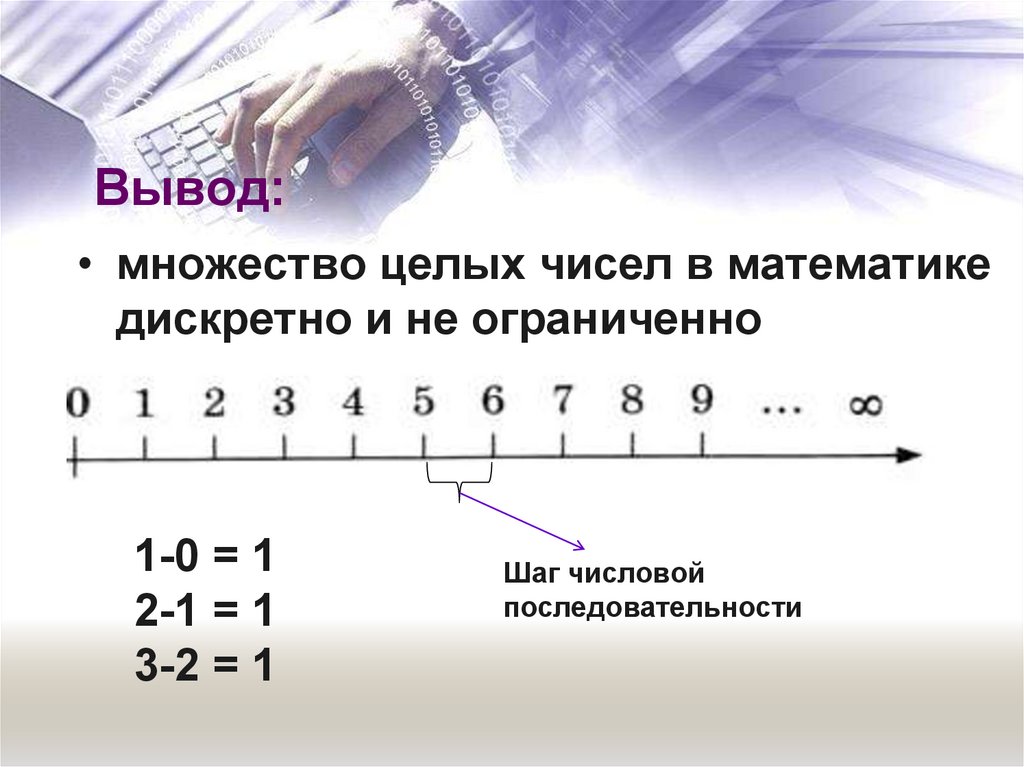
12. Вывод:
• множество целых чисел в математикедискретно и не ограниченно
1-0 = 1
2-1 = 1
3-2 = 1
Шаг числовой
последовательности
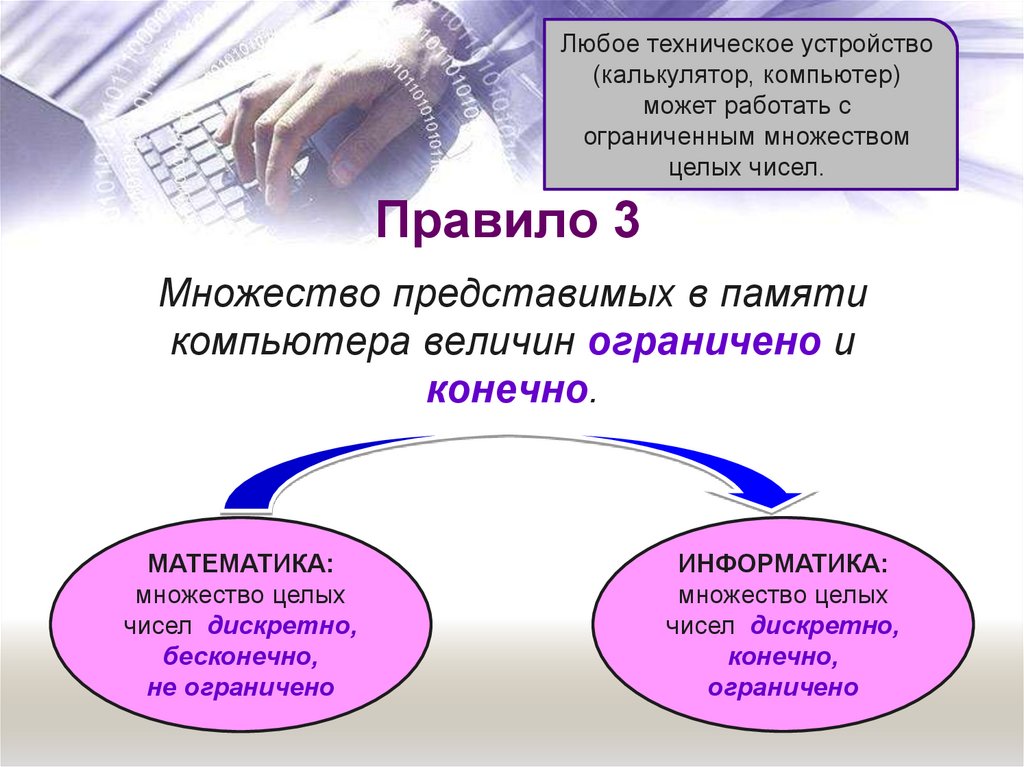
13. Правило 3
Любое техническое устройство(калькулятор, компьютер)
может работать с
ограниченным множеством
целых чисел.
Правило 3
Множество представимых в памяти
компьютера величин ограничено и
конечно.
МАТЕМАТИКА:
множество целых
чисел дискретно,
бесконечно,
не ограничено
ИНФОРМАТИКА:
множество целых
чисел дискретно,
конечно,
ограничено
14. Правило 4
В памяти компьютера числа хранятся вдвоичной системе счисления.
15. Числовые величины
Целые(формат с
фиксированной запятой)
Вещественные
(формат с
плавающей запятой)
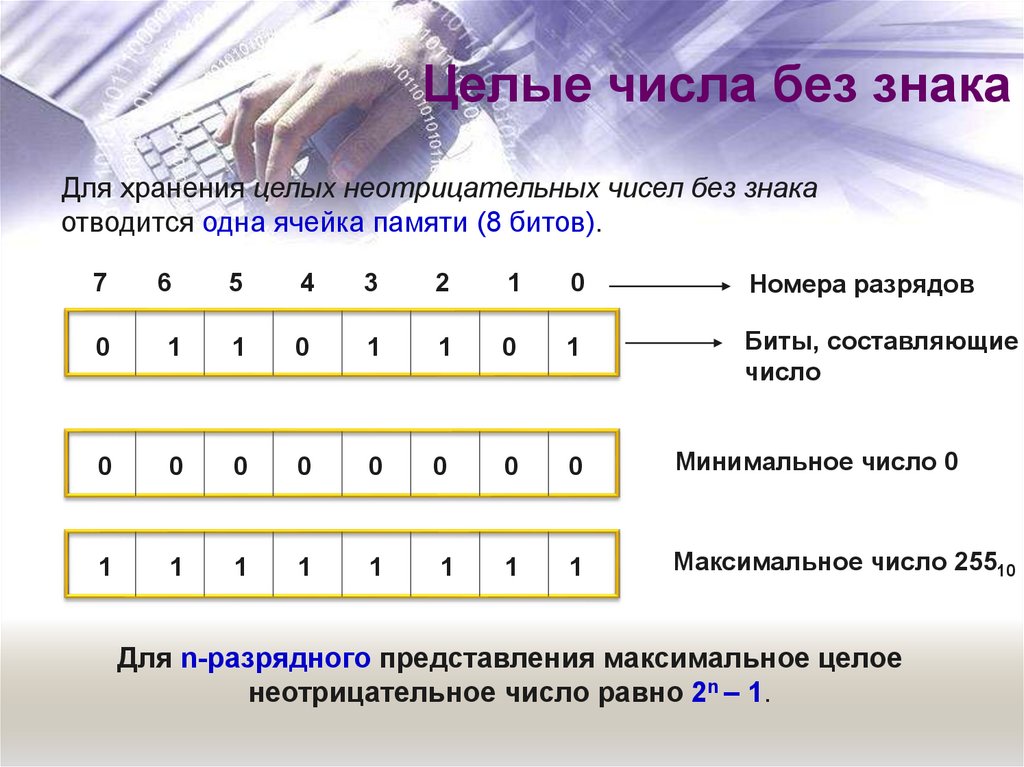
16. Целые числа без знака
Для хранения целых неотрицательных чисел без знакаотводится одна ячейка памяти (8 битов).
7
6
5
4
3
2
1
0
Номера разрядов
0
1
1
0
1
1
0
1
Биты, составляющие
число
0
0
0
0
0
0
0
0
Минимальное число 0
1
1
1
1
1
1
1
1
Максимальное число 25510
Для n-разрядного представления максимальное целое
неотрицательное число равно 2n – 1.
17. Целые числа без знака
Пример. Представить число 5110 в двоичном виде ввосьмибитовом представлении в формате
целого без знака.
Решение.
5110 = 1100112
0
0
1
1
0
0
1
1
18. Целые числа со знаком
Для хранения целых чисел со знаком отводитсядве ячейки памяти (16 битов).
Старший разряд числа определяет его знак.
Если он равен 0, число положительное,
если 1, то отрицательное.
5110 = 1100112
0
0
1
1
0
0
1
1
- 5110 = - 1100112
1
0
1
1
0
0
1
1
Такое представление чисел в компьютере называется
прямым кодом.
19. Целые числа со знаком
Для n-разрядного представления со знаком (с учетомвыделения одного разряда на знак):
•минимальное отрицательное число равно
– 2n-1
•максимальное положительное число равно 2n-1 – 1,
Целые числа в памяти компьютера —
это дискретное, ограниченное и конечное
множество.
20. Целые числа со знаком
Для представления отрицательных целых чисел используетсядополнительный код.
Алгоритм получения дополнительного кода отрицательного числа:
1. Число записать прямым кодом в n двоичных разрядах.
2. Получить обратный код числа, для этого значения всех
битов инвертировать, кроме старшего разряда.
3. К полученному обратному коду прибавить единицу.
Представить число -201410 в двоичном виде в шестнадцатибитном
представлении в формате целого со знаком.
Прямой код
-201410
10000111 110111102
Обратный код
Инвертирование
11111000 001000012
Прибавление единицы
11111000 001000012
00000000 000000012
Дополнительный код
11111000 001000102
21. Целые числа со знаком
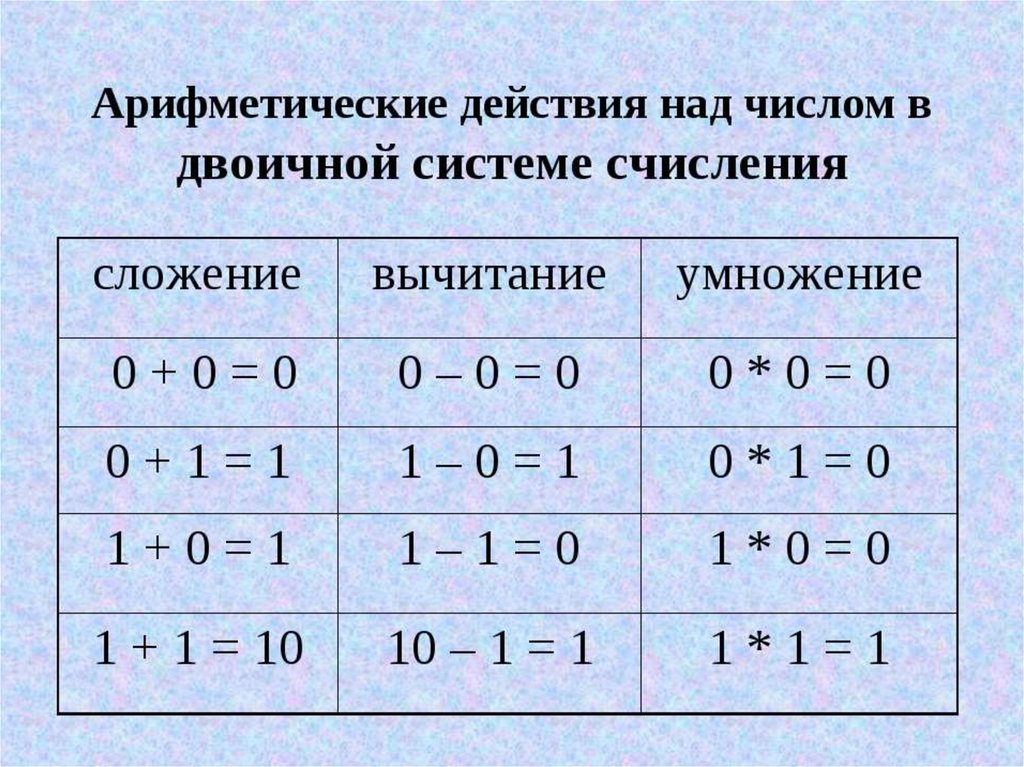
Алгебраическое сложение двоичных чисел1.
Положительные слагаемые представить в прямом коде.
2.
Отрицательные слагаемые – в дополнительном.
3.
Найти сумму кодов, включая знаковые разряды,
которые при этом рассматриваются как старшие
разряды. При переносе из знакового разряда единицу
переноса отбрасывают.
4.
В результате получают алгебраическую сумму в прямом
коде, если эта сумма положительная, и в
дополнительном, если сумма отрицательная.
22. Целые числа со знаком
Пример 1. Найти разность 1310 – 1210 в восьмибитномпредставлении.
1310
– 1210
Прямой код
00001101
10001100
Обратный код
-
11110011
Дополнительный код
-
11110100
0 0001101
+
1 1110100
10 0 0 0 0 0 0 1
Так как произошел перенос из знакового разряда,
первую единицу отбрасываем, и в результате
получаем 00000001.
23. Целые числа со знаком
Пример 2. Найти разность 810 – 1310 в восьмибитномпредставлении.
810
– 1310
Прямой код
00001000
10001101
Обратный код
-
11110010
Дополнительный код
-
11110011
+
0 0001000
1 1110011
1 1111011
24. Целые числа со знаком
Пример 2. Найти разность 810 – 1310 в восьмибитномпредставлении.
+
0 0001000
1 1110011
1 1111011
В знаковом разряде стоит 1, значит результат получен в
дополнительном коде. Перейдем от дополнительного кода к
обратному, вычитая единицу:
1 1110011
0 0000001
1 1111010
Перейдем от обратного кода к прямому, инвертируя все цифры, за
исключением знакового (старшего) разряда: 100001012 = -510.
25. Вещественные числа
Вещественные числа хранятся и обрабатываются вкомпьютере в формате с плавающей запятой,
использующем экспоненциальную форму записи чисел.
n
A=M q
M – мантисса числа (правильная отличная от нуля дробь),
q – основание системы счисления,
n – порядок числа.
Диапазон ограничен максимальными значениями M и n.
26. Вещественные числа
Например, 123,45 = 0,12345 · 103Порядок указывает, на какое количество позиций и в каком
направлении должна сместиться десятичная запятая в мантиссе.
Число в формате с плавающей запятой может
занимать в памяти 4 байта (обычная точность) или 8
байтов (двойная точность).
При записи числа выделяются разряды для хранения
знака мантиссы, знака порядка, порядка и мантиссы.
Мантисса M и порядок n определяют диапазон
изменения чисел и их точность.
27. Пример: представить число -123,45 в 4-х байтовом представлении (обычная точность)
• Представим число в нормализованном виде:0,12345 103
• Число отрицательное, поэтому старший бит (31)=1
• Порядок 3-положительный, значит след.бит (30)=0
• Число 3 в 2-ой СС имеет вид: 11, записываем его в остальных 6 битах
старшего байта, дополняя слева незначащими нулями
• Найдем двоичное представление мантиссы, умножив её
последовательно на 2 24 раза, записывая целую часть от умножения
сверху вниз
1 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1 0 0 1 1 0 1 0 0 1 1 0 1 0 1 1
м а
н
т и
с
с
а
28. Графический диктант:
Если утверждение верно, ставим знак _ , еслиневерно – знак /\ .
1.Система счисления – это способ представления
чисел и соответствующие ему правила действий
над числами.
2.Информация, хранящаяся в компьютере,
представлена в троичной системе счисления.
3.В двоичной системе счисления 11 + 1 = 12.
4.В позиционных системах счисления
количественный эквивалент цифры зависит от её
местоположения в записи числа.
5.В 16-ричной системе счисления символ F
используется для обозначения числа 15.
29. Домашнее задание:
• §5 (прочитать, работать с записями втетради, подготовиться к с/р)
• Задания 3 и 4 после параграфа письменно в тетрадях.























 informatics
informatics








