Представление чисел в памяти компьютера

1. Представление чисел в памяти компьютера

Домашнее задание:
§2.10
Задания №№ 2.14 – 2.15 на стр. 147-148

2.

Числа
Целые
Вещественные
2

3. Целые числа

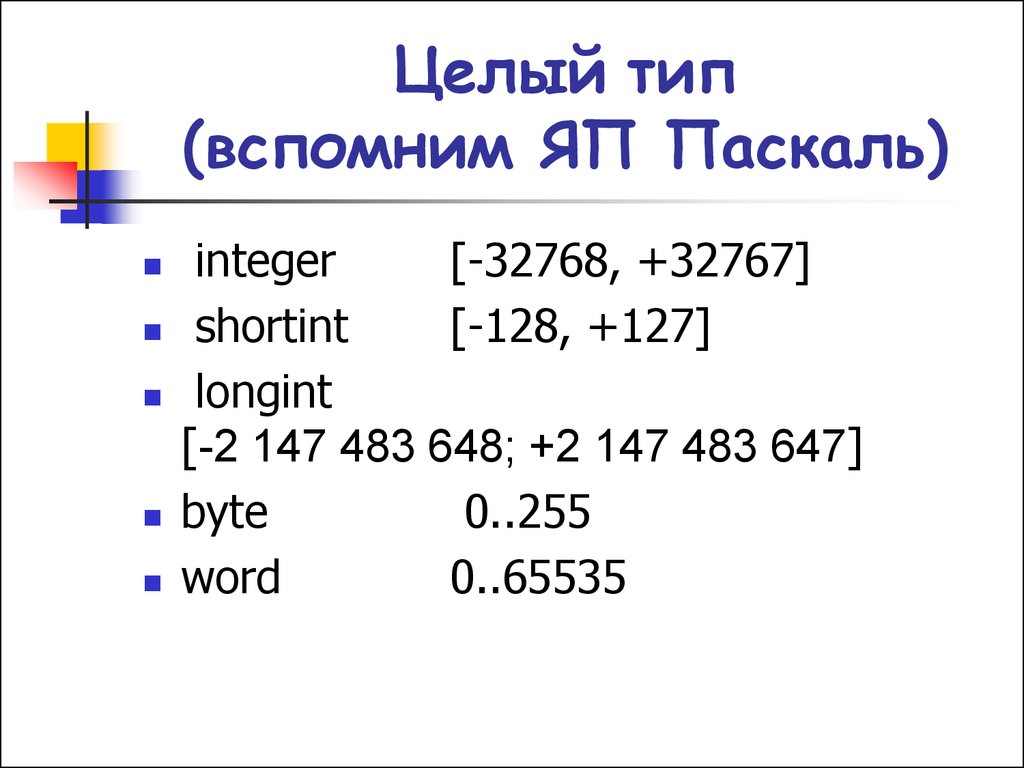
4. Целый тип (вспомним ЯП Паскаль)

integer
[-32768, +32767]
shortint
[-128, +127]
longint
[-2 147 483 648; +2 147 483 647]
byte
0..255
word
0..65535

5. Целые числа

хранятся
в
памяти
компьютера в формате
с фиксированной запятой
5

6.

Целые числа
Неотрицательные (без знака)
Со знаком
6

7. Представление чисел в формате с фиксированной запятой

Целые неотрицательные числа (0, 1, …)
Целые числа со знаком (+45, -12)
7

8. Целый тип

integer
[-32768, +32767]
shortint
[-128, +127]
longint
[-2 147 483 648; +2 147 483 647]
byte
0..255
word
0..65535

9. Целые неотрицательные числа

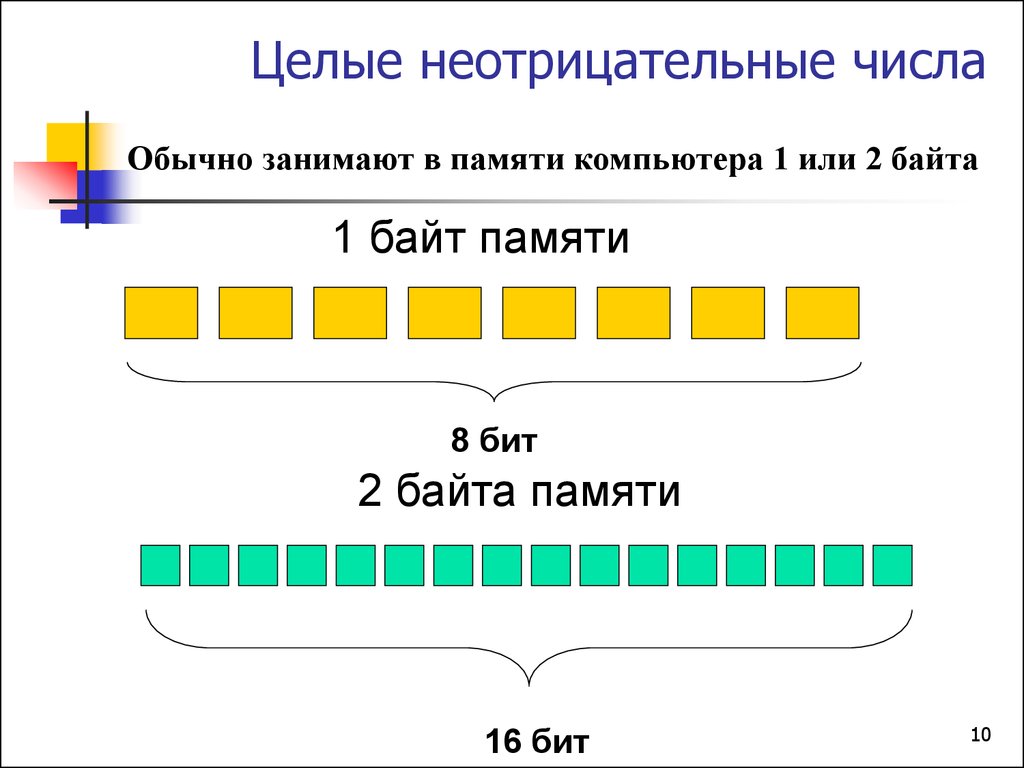
10. Целые неотрицательные числа

Обычно занимают в памяти компьютера 1 или 2 байта
1 байт памяти
8 бит
2 байта памяти
16 бит
10

11.

Целые неотрицательные числа
Число 110011102 = 20610
1
1
0
0
1
1
1
0
8 бит
0
0
0
0
0
0
0
0
1
1
0
0
1
1
1
0
16 бит
11

12.

Целые неотрицательные числа
Число 101102 = 2210
0
0
0
1
0
1
1
0
8 бит
0
0
0
0
0
0
0
0
0
0
0
1
0
1
1
0
16 бит
12

13.

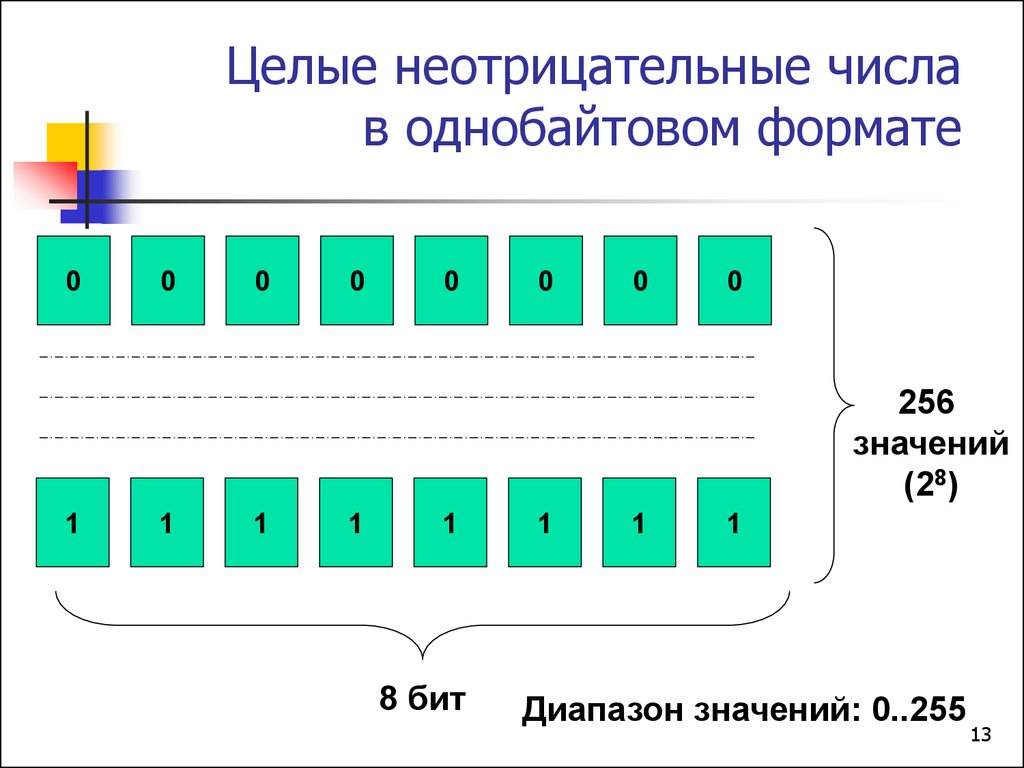
Целые неотрицательные числа
в однобайтовом формате
0
0
0
0
0
0
0
0
256
значений
(28)
1
1
1
1
1
8 бит
1
1
1
Диапазон значений: 0..255
13

14.

Целые неотрицательные числа
в двухбайтовом формате
Диапазон значений???????
14

15. Целый тип

integer
[-32768, +32767]
shortint
[-128, +127]
longint
[-2 147 483 648; +2 147 483 647]
byte
0..255
word
0..65535

16. Целые числа со знаком

17. Целые числа со знаком

Обычно занимают в памяти компьютера
1, 2 или 4 байта
Самый левый (старший) разряд содержит
информацию о знаке числа
Знак «плюс» кодируется нулем, а «минус» единицей
17

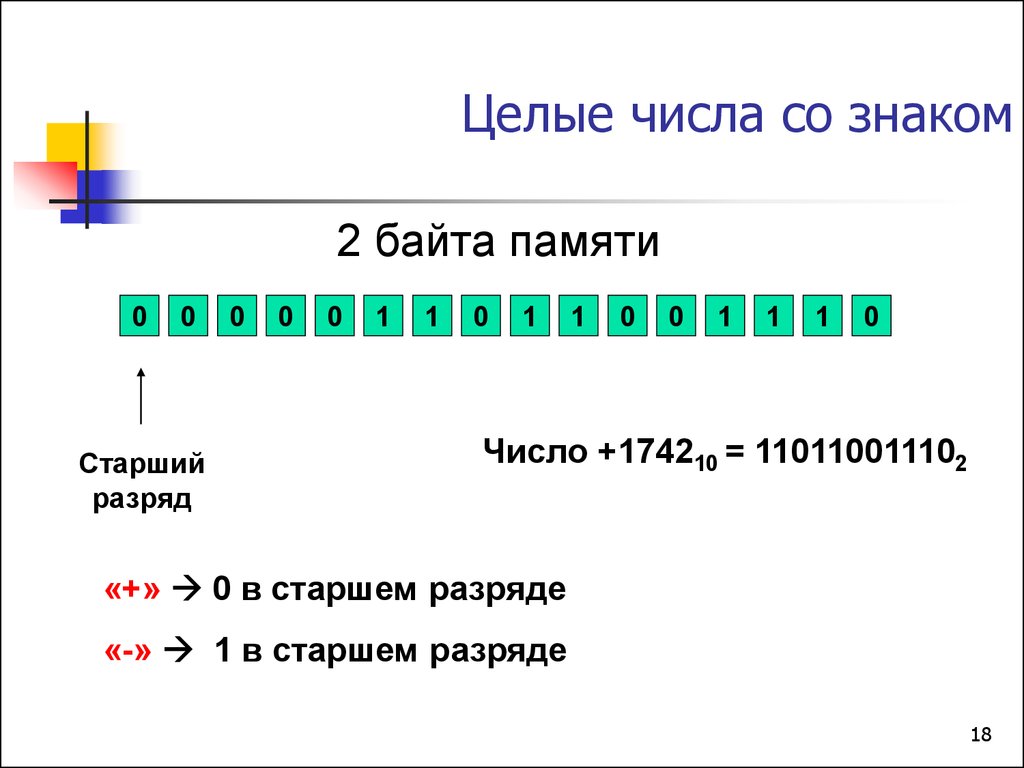
18. Целые числа со знаком

2 байта памяти
0
0
Старший
разряд
0
0
0
1
1
0
1
1
0
0
1
1
1
0
Число +174210 = 110110011102
«+» 0 в старшем разряде
«-» 1 в старшем разряде
18

19.

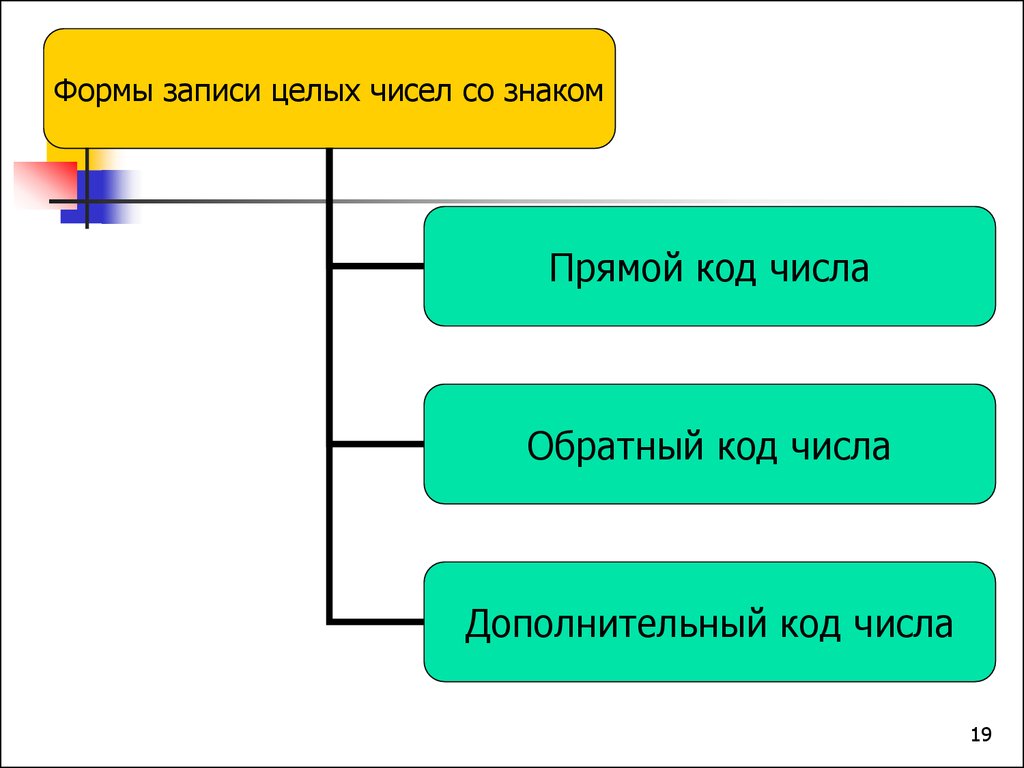
Формы записи целых чисел со знаком
Прямой код числа
Обратный код числа
Дополнительный код числа
19

20. Целые числа со знаком

Положительные числа в прямом,
обратном и дополнительном кодах
изображаются одинаково
20

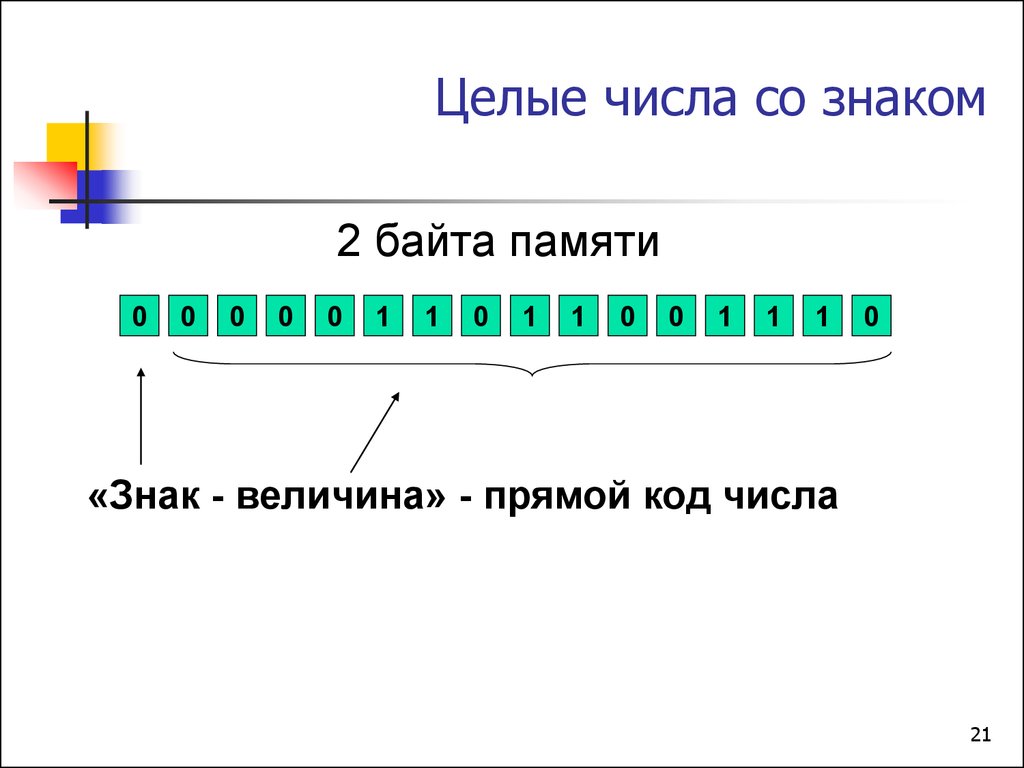
21. Целые числа со знаком

2 байта памяти
0
0
0
0
0
1
1
0
1
1
0
0
1
1
1
0
«Знак - величина» - прямой код числа
21

22. Целые числа со знаком

Отрицательные числа в прямом,
обратном и дополнительном кодах
имеют разное изображение
22

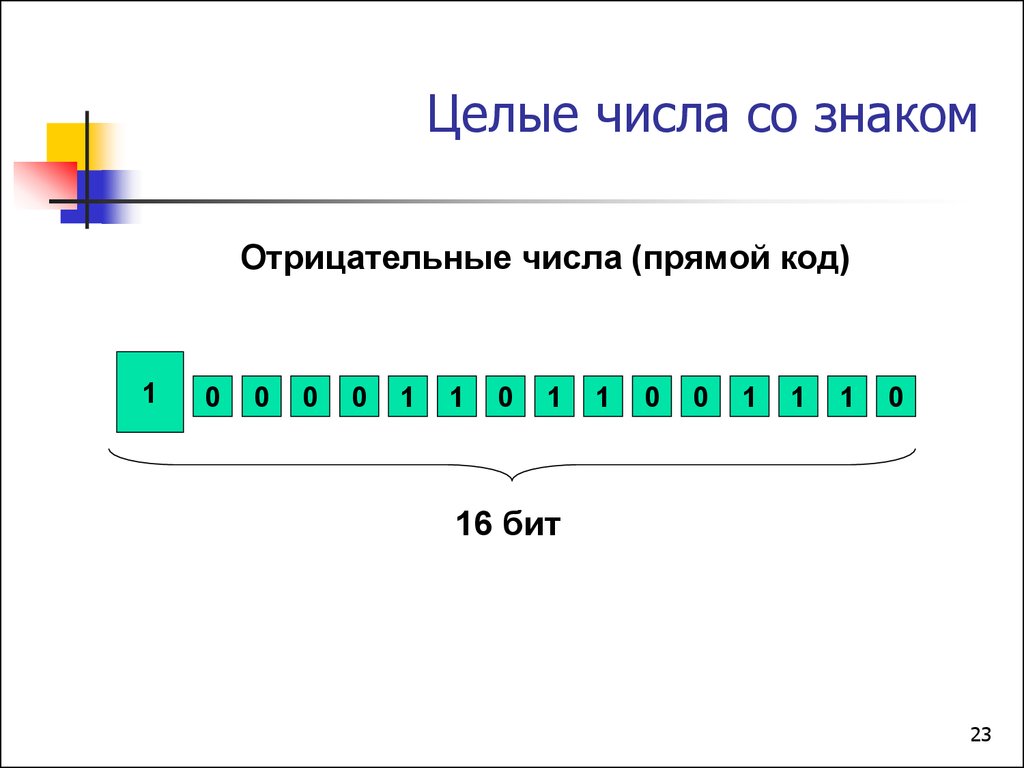
23. Целые числа со знаком

Отрицательные числа (прямой код)
1
0
0
0
0
1
1
0
1
1
0
0
1
1
1
0
16 бит
23

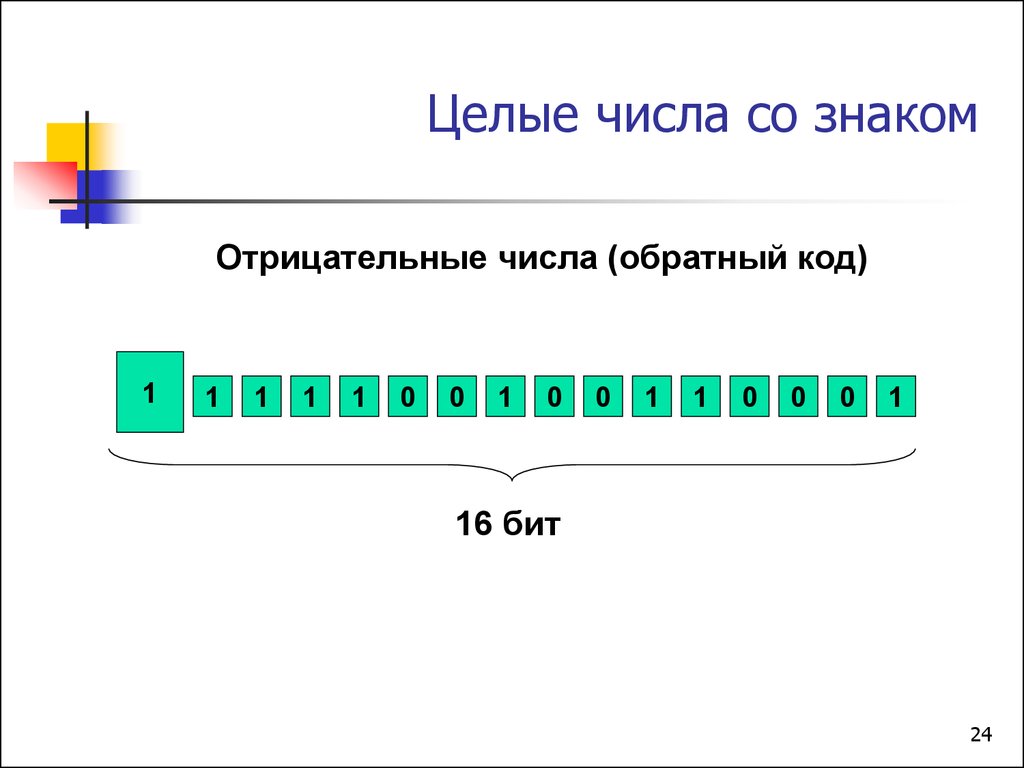
24. Целые числа со знаком

Отрицательные числа (обратный код)
1
1
1
1
1
0
0
1
0
0
1
1
0
0
0
1
16 бит
24

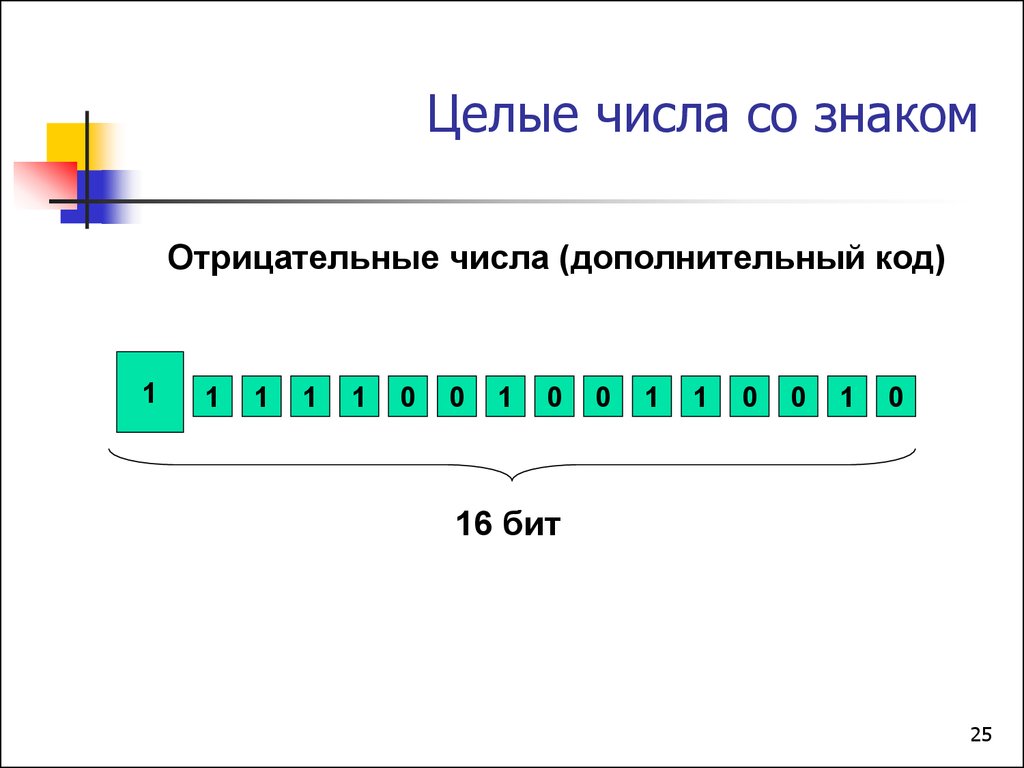
25. Целые числа со знаком

Отрицательные числа (дополнительный код)
1
1
1
1
1
0
0
1
0
0
1
1
0
0
1
0
16 бит
25

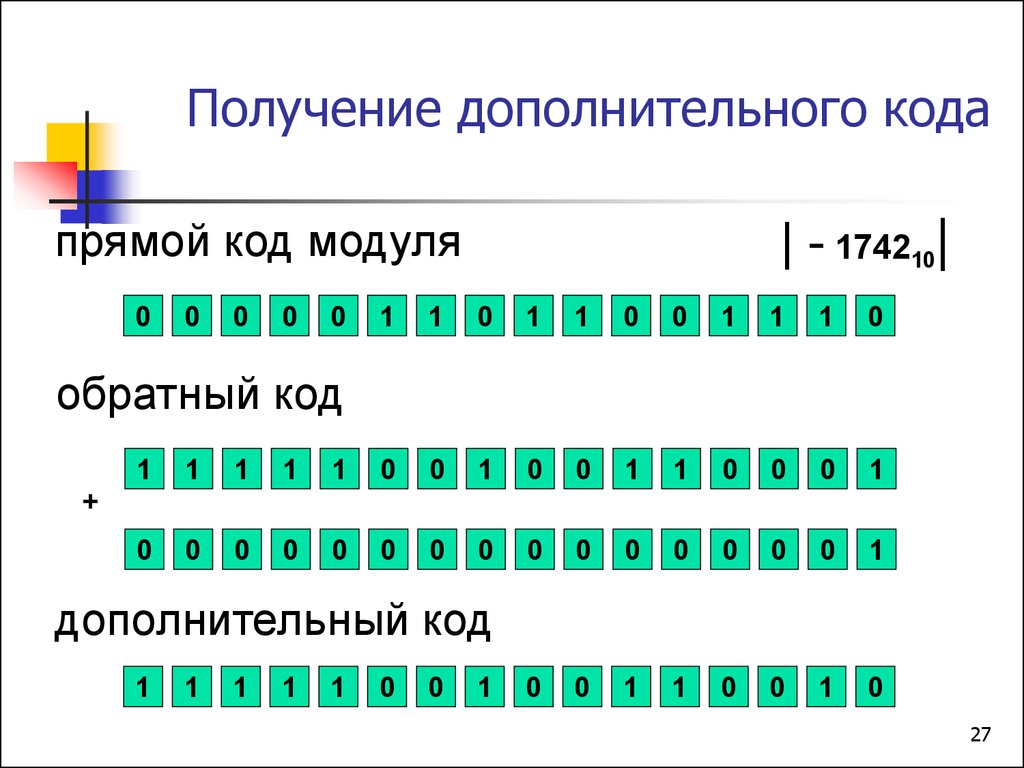
26. Получение дополнительного кода

- 174210
1. Записать прямой код модуля |-1742|
2. Получить обратный код (инвертирование
прямого кода)
3. Получить дополнительный код
прибавлением единицы к обратному коду
26

27. Получение дополнительного кода

прямой код модуля
0
0
0
0
0
| - 174210|
1
1
0
1
1
0
0
1
1
1
0
обратный код
1
1
1
1
1
0
0
1
0
0
1
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
1
0
0
1
0
+
дополнительный код
1
1
1
1
1
0
0
1
27

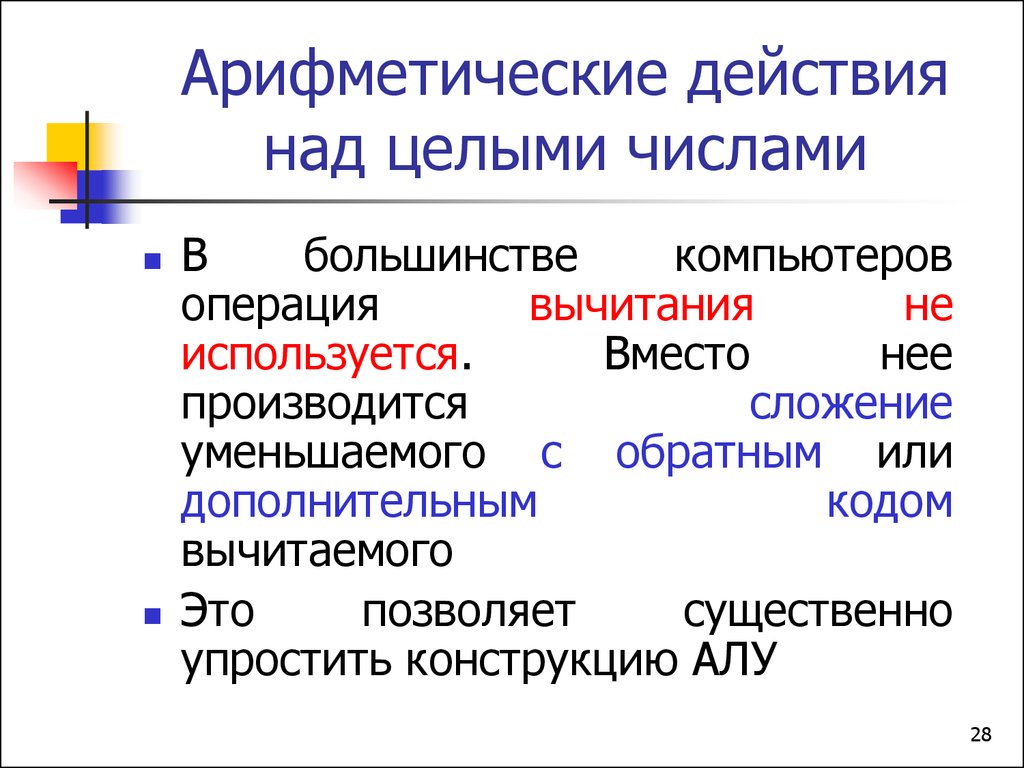
28. Арифметические действия над целыми числами

В
большинстве
компьютеров
операция
вычитания
не
используется.
Вместо
нее
производится
сложение
уменьшаемого с обратным или
дополнительным
кодом
вычитаемого
Это
позволяет
существенно
упростить конструкцию АЛУ
28

29. Целые числа со знаком

1 байт
1 разряд для знака
27 – 1 = 127
– 27 = – 128
Диапазон значений: – 128.. 127
29

30. Целые числа со знаком

2 байта
1 разряд для знака
215 – 1 = 32767
– 215 = – 32768
Диапазон значений: – 32768.. 32767
30

31. Целые числа со знаком

4 байта
1 разряд для знака
231 – 1 = 2 147 483 647
– 231 = – 2 147 483 648
Диапазон значений:
– 2 147 483 648 .. 2 147 483 647
31

32. Целый тип

integer
[-32768, +32767]
shortint
[-128, +127]
longint
[-2 147 483 648; +2 147 483 647]
byte
0..255
word
0..65535

33. Вещественные числа

34. Вещественный тип

real
-0.1Е -39 .. 1.0Е+38
(точность 11 десятичных знаков)
single
double
7 десятичных цифр
15 десятичных цифр

35. Вещественные числа

хранятся
в
памяти
компьютера в формате
с плавающей запятой
Обычно занимают в памяти
компьютера 4, 6, 8 или 10
байт
35

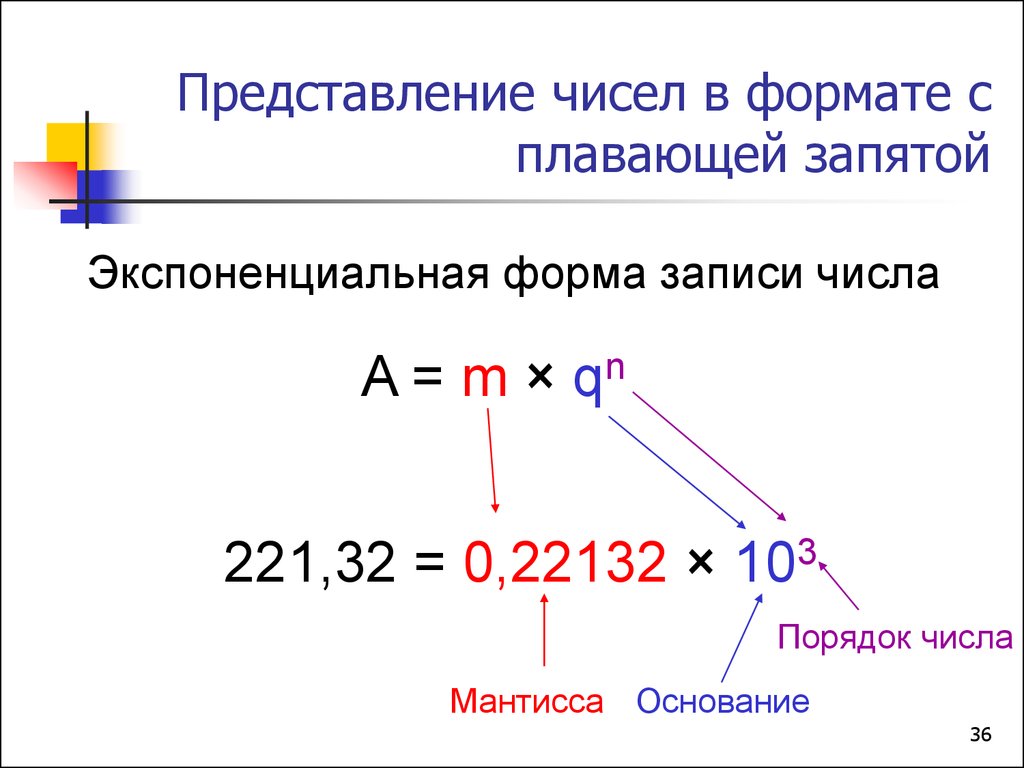
36. Представление чисел в формате с плавающей запятой

Экспоненциальная форма записи числа
A = m × qn
221,32 = 0,22132 × 103
Порядок числа
Мантисса Основание
36

37. Нормализованная запись вещественных чисел

A = m × qn, где мантисса
принадлежит промежутку [0.1, 1)
Если число записано в системе
счисления с основанием q, то мантиссу
и порядок числа принято записывать в
этой
же
системе
счисления
(с
основанием
q),
а само основание – в 10 системе.
37

38. Упражнение

-6.2510 =
-110.012 =
112
-0.110012*210
38

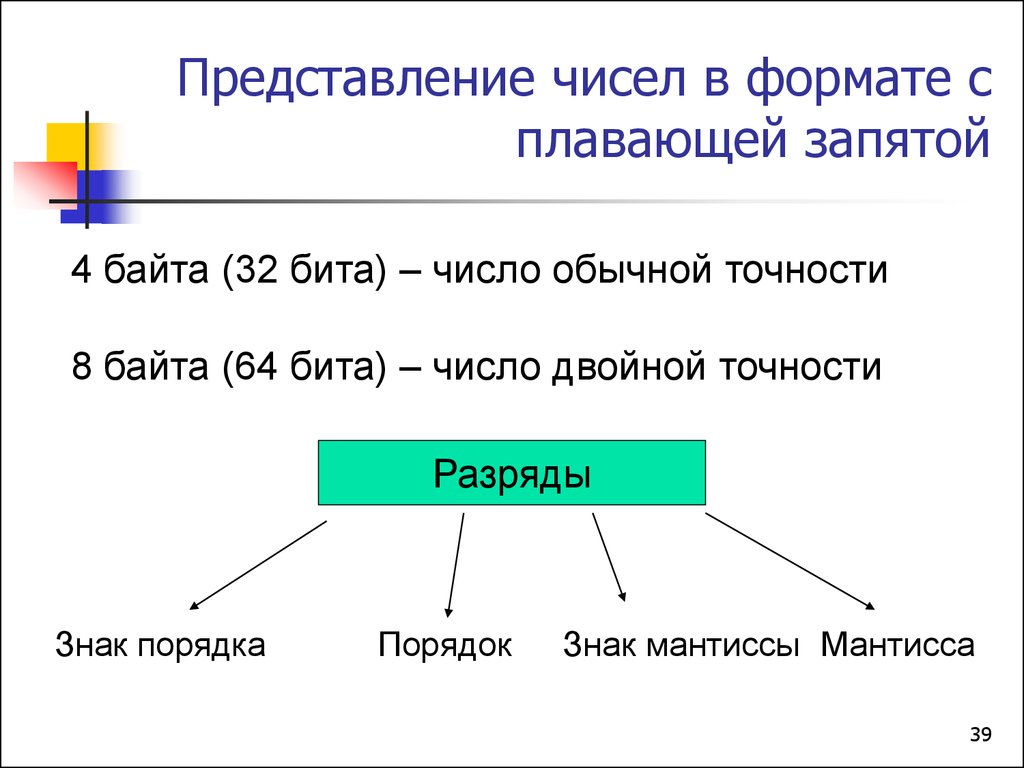
39. Представление чисел в формате с плавающей запятой

4 байта (32 бита) – число обычной точности
8 байта (64 бита) – число двойной точности
Разряды
Знак порядка
Порядок
Знак мантиссы Мантисса
39

40. Представление чисел в формате с плавающей запятой

4 байта (32 бита) – число обычной точности
Знак порядка – 1 разряд
8 разрядов
Порядок – 7 разрядов
Знак мантиссы – 1 разряд
Мантисса – 23 разряда
24 разряда
40

41.

Представление чисел в формате с
плавающей запятой
-6.2510 =
0 0 0 0 0 0 1 1
112
-0.110012*210
1 1 1 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
41

42. Представление чисел в формате с плавающей запятой

4 байта (32 бита) – число обычной точности
Максимальное значение порядка: 11111112 = 12710
Максимальное значение числа: 2127
Максимальное значение положительной мантиссы: 223-1
42

43. Представление чисел в компьютере

Представление чисел в формате с
фиксированной запятой
целых неотрицательных чисел (2 байта?
– диапазон значений?)
целых чисел со знаком (положительных
и отрицательных)
Представление чисел в формате с
плавающей запятой
43