Множества и логика. Логические основы компьютеров

1. Логические основы компьютеров

1
Логические
основы
компьютеров
§ 21. Множества и логика

2. Что нужно знать о множествах?

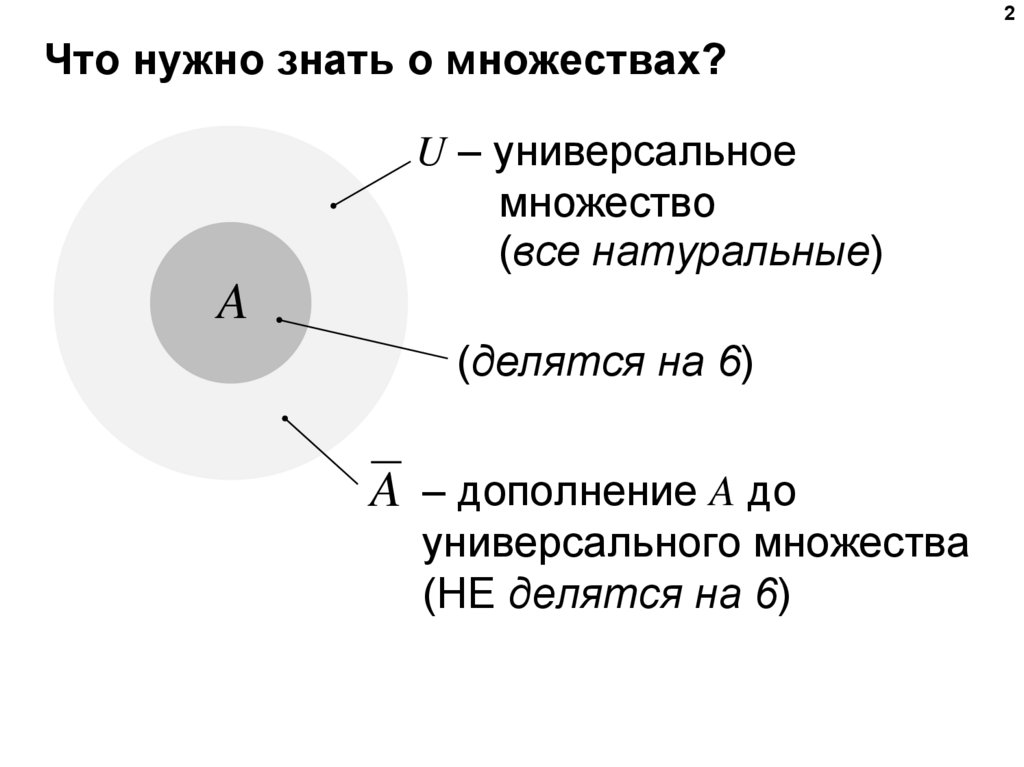
2
Что нужно знать о множествах?
U – универсальное
множество
(все натуральные)
A
(делятся на 6)
A – дополнение A до
универсального множества
(НЕ делятся на 6)

3. Что нужно знать о множествах?

3
Что нужно знать о множествах?
A
B
A·B – пересечение (A B)
A
B
A+B – объединение (A B)

4. Множества и логические функции

4
Множества и логические функции
Множество задаётся логической функцией
A
x A
A(x) = 1
A
A( x) 1 x A
x A
A
B
A( x) B( x) 1 x A·B
A
B
A( x) B( x) 1 x A+B

5. Задача дополнения (I)

5
Задача дополнения (I)
Задача 1. Каким должно быть множество A для того,
чтобы множество A + B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
это решение!
B B U A B
B ( x) 1
это условие
? Есть ли другие решения?
A
определяет нужное
множество A
A включает B
(A B)
C B B U Amin B

6. Задача дополнения (II)

6
Задача дополнения (II)
Задача 2. Каким должно быть множество A для того,
чтобы множество A B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
B B U A B A B
B( x ) 1
это условие
это решение!
? Есть ли другие решения?
A
определяет нужное
множество A
A включает B
(A B)
C B B U ( A ) min B
A B
Amax B

7. Общий подход к решению

7
Общий подход к решению
1. Свести задачу к одной из базовых задач
Задача 1. A B 1
B A 1
Задача 2. A B 1 B A 1
2. Использовать готовое решение:
Задача 1. Amin B
Задача 2. Amax B

8. Задачи с отрезками

8
Задачи с отрезками
На числовой прямой даны два отрезка:
P = [37; 60] и Q = [40; 77]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
P (Q A P )
A = (x A)

9. Задачи с отрезками

9
Задачи с отрезками
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = [37; 60], Q = [40; 77]
Amin = [40; 60]
длина 20

10. Задачи с отрезками-II

10
Задачи с отрезками-II
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наибольшую
возможную длину такого отрезка A, что
выражение
(x A) → ((x P) (x Q))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
A ( P Q)
A = (x A)

11. Задачи с отрезками-II

11
Задачи с отрезками-II
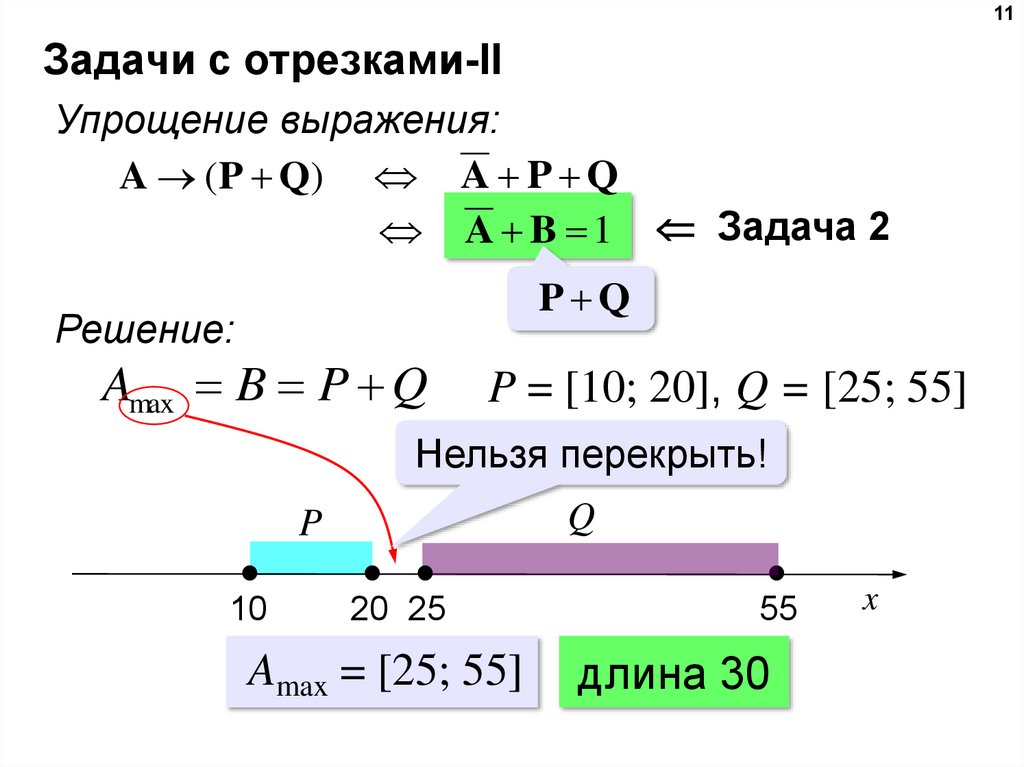
Упрощение выражения:
A ( P Q) A P Q
A B 1 Задача 2
P Q
Решение:
Amax B P Q
P = [10; 20], Q = [25; 55]
Нельзя перекрыть!
Q
P
10
20 25
Amax = [25; 55]
55
длина 30
x

12. Задачи с отрезками-III

12
Задачи с отрезками-III
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
((x P) (x Q)) → (x A)
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
(P Q) A
A = (x A)

13. Задачи с отрезками-III

13
Задачи с отрезками-III
Упрощение выражения:
(P Q) A A P Q
A B 1
Задача 1
P Q
Решение:
Amin B P Q
P
10
P = [10; 20], Q = [25; 55]
Нужно перекрыть!
Q
20 25
Amin = [10; 55]
55
длина 45
x

14. Множества чисел

14
Множества чисел
Элементами множеств А, P и Q являются
натуральные числа, причём
P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}.
Известно, что выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Определите наименьшее возможное значение суммы
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
P (Q A P )
A = (x A)

15. Множества чисел

15
Множества чисел
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = {2, 4, 6, 8, 10, 12}, Q = {4, 8, 12, 116}
Amin = {4, 8, 12}
сумма 24

16. Множества чисел-II

16
Множества чисел-II
Элементами множеств А, P и Q являются
натуральные числа, причём
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }.
Известно, что выражение
((x A) → ¬(x P)) (¬(x Q) → ¬(x A))
истинно при любом значении переменной х.
Определите наибольшее возможное количество
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
( A P ) ( Q A)
A = (x A)

17. Множества чисел-II

17
Множества чисел-II
Упрощение выражения:
(A P) (Q A) ( A P) (Q A)
A Q P Q A P A
A Q P Q A
A P Q
A B 1 Задача 2
Решение:
Amax B P Q
P Q
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }
Amax = { 3, 9, 15, 21, 24, 27, 30 }
7 шт.