Влияние атмосферы на геодезические измерения

1.

Влияние атмосферы на геодезические измерения
1

2.

Влияние атмосферы на геодезические измерения
Все геодезические измерения выполняют в атмосфере.
Атмосфера – среда неоднородная, т.е. ее свойства меняются от точки к точке.
Оптическую плотность атмосферы характеризует показатель преломления n.
Он представляет собой отношение скорости c света в вакууме к скорости v
излучения в рассматриваемой среде:
n
c
c
v
v
n
Часто вместо показателя преломления используют индекс преломления, равный
отличию показателя преломления от 1, увеличенному в миллион раз:
N n 1 106
Показатель преломления – величина безразмерная.
Индекс преломления выражают в N-единицах:
1 N-ед.=10-6
2

3.

Влияние атмосферы на геодезические измерения
В неоднородной атмосфере показатель преломления меняется, что приводит к
ошибкам в геодезических измерениях.
В линейных измерениях фактический показатель преломления отличается от
используемого при вычислении расстояния:
D v τ
c τ
.
n
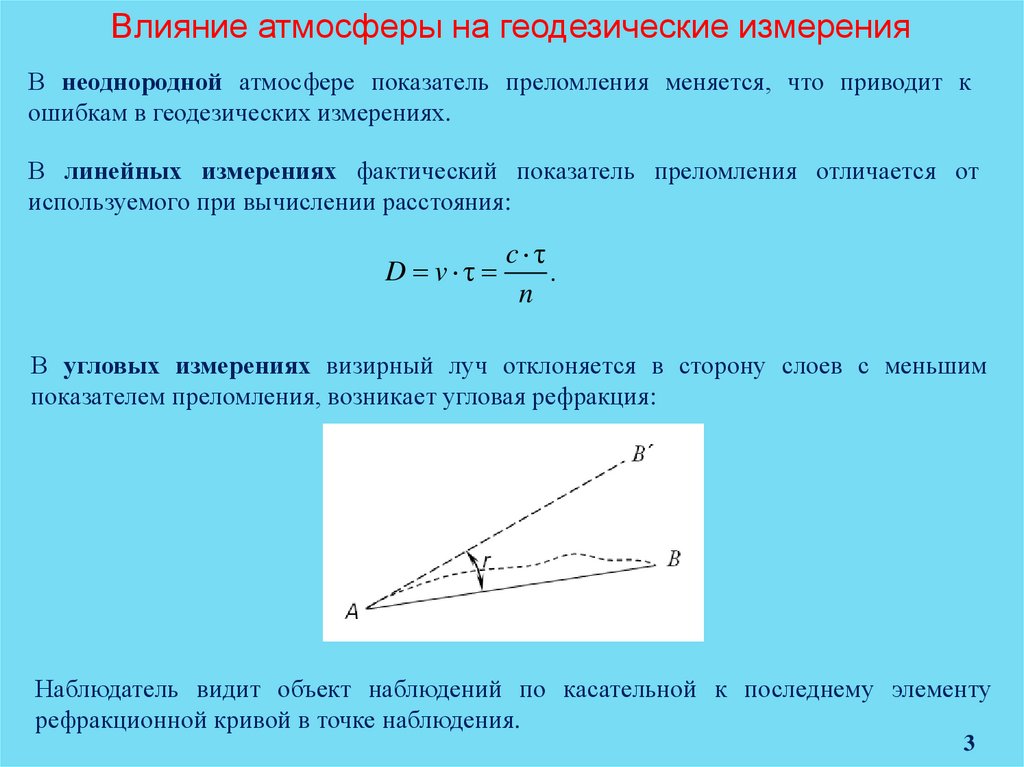
В угловых измерениях визирный луч отклоняется в сторону слоев с меньшим
показателем преломления, возникает угловая рефракция:
Наблюдатель видит объект наблюдений по касательной к последнему элементу
рефракционной кривой в точке наблюдения.
3

4.

Влияние атмосферы на геодезические измерения
Величина ошибки зависит от интенсивности изменения показателя преломления,
которая характеризуется градиентом показателя преломления:
grad n
n
.
y
Градиент показателя преломления имеет размерность м-1.
Угол рефракции связан с градиентом показателя преломления формулой Ньютона:
ρ
ρ D
r grad n x dx
grad ср n.
D0
2
D
Градиент показателя преломления, равный 10-8/м, приводит к формированию угла
рефракции, равного 1 секунде, на дистанции 1 км.
Это соответствует ошибке 5 мм в
определении положения конечной точки дистанции:
r D
1 103
hr S
0, 005 м.
5
2,06 10
hr (Δs)
Боковая рефракция такого порядка формируется на границах раздела резко
отличающихся подстилающих поверхностей.
Вертикальная рефракция может превышать это значение на несколько порядков.
4

5.

Влияние атмосферы на геодезические измерения
Влияние ошибки определения показателя преломления на точность измерения
расстояний можно оценить, используя истинную или среднюю квадратическую
ошибки показателя преломления:
D D n.
mD D mn .
Ошибка определения показателя преломления, равная 1 N-ед., приводит к ошибке в
расстоянии, равной 1 мм/км.
ρ D
mr
mgrad n
2
В угловых измерениях ошибка определения градиента показателя
преломления, равная 10-8/м, приводит к ошибке в измеренном угле,
равной 1 секунде, на дистанции 1 км. Это соответствует ошибке 5
мм в определении положения конечной точки дистанции.
5

6.

Показатель преломления и его градиент
как функции метеопараметров
Показатель преломления зависит от температуры Т, давления р и влажности е
(парциального давления водяного пара) воздуха.
Кроме того, в оптическом диапазоне надо учитывать длину волны излучения!
Для световых волн для определения эффективного группового индекса преломления
используют формулу Сирса-Баррела:
p
e
N опт n 1 106 83,11 11, 4 .
T
T
Зависимость индекса преломления радиоволн от метеопараметров в нейтральной
атмосфере описывает формула Фрума-Эссена:
N радио n 1 106 77,63
p
e
e
12,92 371914 2
T
T
T
6

7.

Показатель преломления и его градиент
как функции метеопараметров
Оценить влияние ошибок определения метеопараметров на ошибку показателя
преломления позволяют формулы:
N
N
N
N
T
p
e,
T
p
e
2
N 2 N 2 N 2
m N
mp
mT
me
T
e
p
2
2
и таблица частных производных:
Производная
Оптический
диапазон
Радиодиапазон
∂n/∂T
1 10 6 K
1,3 10 6 K
∂n/∂p
0,3 10 6 гПа
0,3 10 6 гПа
∂n/∂e
0,04 10 6 гПа
4,3 10 6 гПа
7

8.

Показатель преломления и его градиент
как функции метеопараметров
Производная
Оптический
диапазон
∂n/∂T
1 10 6 K
∂n/∂p
0,3 10 6 гПа
∂n/∂e
0,04 10 6 гПа
Для градиента показателя преломления справедливы формулы:
grad n 1 10 6 grad T 0,3 10 6 grad p 0,04 10 6 grad e.
mgrad n
2
6
2
6
2
0,3
10
m
0,04
10
m
1 10 6 mgrad
T
grad p
grad e
2
2
2
8

9.

Показатель преломления и его градиент
как функции метеопараметров. Выводы
Производная
Оптический
диапазон
Радиодиапазон
∂n/∂T
1 10 6 K
1,3 10 6 K
∂n/∂p
0,3 10 6 гПа
0,3 10 6 гПа
∂n/∂e
0,04 10 6 гПа
4,3 10 6 гПа
Для линейных измерений:
1. в оптическом диапазоне влияние влажности на два порядка меньше;
2. для определения показателя преломления с точностью 1 N-ед. температуру,
давление и влажность надо определять с точностью близкой к 1 °С, 2 гПа и 14 гПа,
соответственно;
3. на расстояниях, сравнимых с дальностью действия электронного тахеометра,
влияние изменений метеопараметров крайне редко превышает приборную
погрешность;
4. для учета влияния атмосферы на результаты наземных линейных измерений в
массовом геодезическом производстве достаточно измерить метеопараметры в
точке стояния прибора.
9

10.

Показатель преломления и его градиент
как функции метеопараметров. Выводы
Для угловых измерений:
1. для определения градиента показателя преломления с точностью 10-8/м градиенты
метеопараметров надо определять с точностью, близкой к 0,01 °С/м, 0,02 гПа/м и 0,14 гПа/м,
соответственно;
2. такие требования к точности лежат за пределами точностных возможностей современных
полевых метеодатчиков;
3. к формированию угла рефракции, равного 1'' приводят градиенты метеопараметров, равные
перечисленным выше значениям;
4. в горизонтальной плоскости на расстояниях, сравнимых с дальностью действия электронных
тахеометров, на формирование боковой рефракции заметно влияют только градиенты
температуры;
5. в вертикальной плоскости реальные значения градиентов давления и температуры
практически всегда превышают указанные значения на несколько порядков.
Влияние угловой рефракции можно ослабить, но практически нельзя учесть
(вычислить поправку) с геодезической точностью.
Приемы ослабления влияния угловой рефракции, используемые в геодезии:
уменьшение длины дистанции;
увеличение высоты визирного луча (градиенты больше у поверхности земли);
производство измерений в моменты утренней и вечерней изотермии воздуха.
10

11.

Учет влияния нейтральной атмосферы
на результаты наземных линейных измерений
Использование нормального индекса преломления
в электронной тахеометрии
c
D
n
В нейтральной атмосфере:
N опт n 1 106 f T , p, e,
Nikon NPL-632 (λ=870 нм)
N n 1 106 79,51
p
T
Нормальные условия
t
+20 °C
p
1013,25 гПа
e
13,33 гПа
Nikon NPL-632 (λ=870 нм)
N норм 275 N -ед.
11

12.

Учет влияния нейтральной атмосферы
на результаты наземных линейных измерений
Алгоритм вычисления поправки в измеренное расстояние
1. Определение фактических значений температуры и давления
- ввод с клавиатуры
- измерение встроенными в тахеометр датчиками
2. Вычисление фактического индекса преломления
3. Вычисление поправки ppm:
ppm N норм N N в мм/км
4. Вычисление поправки в измеренное расстояние:
D ppm D км
12

13.

Влияние нейтральной АС на спутниковые измерения
В нейтральной АС
N радио n радио 1 106 f T , p, e
Формула Фрума-Эссена N радио n радио 1 106 77,63 12,92 371914
p
T
e
T
e
T2
Тропосферная задержка dтроп характеризует совокупное влияние
тропосферы и стратосферы:
Dвак с троп Dтроп vтроп троп
d троп Dвак Dтроп
Dвак и Dтроп - расстояние, пройденное радиосигналом за время τтроп, в
вакууме и тропосфере
Тропосферная задержка формируется в нижних (40-45) км и
составляет около (2,3-2,5) м для спутника, расположенного в зените.
13

14.

Учет влияния нейтральной АС на спутниковые измерения
Модели тропосферной задержки:
1. Статистические – содержат статистические параметры,
характеризующие среднее состояние АС (ошибка определения
зенитной задержки – несколько дециметров).
2. Комбинированные – используют информацию о фактическом
состоянии АС и статистические параметры (ошибка
определения зенитной задержки – несколько сантиметров).
К комбинированным моделям относится, например, модель Хопфильд, в которой
используется информация о температуре, давлении и влажности с точке стояния
спутникового приемника.
С учетом высоты спутника над горизонтом указанные значения ошибок могут
возрасти в несколько раз.
Уменьшить влияние ошибок моделирования тропосферной задержки позволяют
относительный и дифференциальные методы спутниковых измерений: если
ошибки моделирования одинаковые для базовой и определяемой станций, их
влияние исключается при вычислении разностей координат или при введении
дифференциальных поправок.
14

15.

Определение ионосферной задержки.
Модель Клобучара
Суть
1. Представляет ионосферную задержку в виде функции от местного
времени и геомагнитной широты.
2. На постоянную 5 нс накладывается дневная составляющая в виде
косинусоидальной полуволны, описывающей зависимость от времени.
3. Зависимость от геомагнитной широты задана полиномом 3-ей степени.
4. Коэффициенты полинома передаются в навигационном сообщении и
обновляются каждые 6 дней.
Ограничения
• недостаточно частое обновление коэффициентов модели приводит к
отличию текущего состояния ионосферы от смоделированного;
• постоянство ночных значений ионосферной задержки не соответствует
реальности, после захода TEC плавно уменьшается, достигая минимума
перед восходом;
• максимум ионосферной задержки не всегда приходится на 14 часов
местного времени.
15

16.

Ослабление влияния ионосферной задержки.
Дисперсионный метод
Ионосфера – диспергирующая среда для радиоволн!
1. Измерения выполняют на двух частотах.
2. Дальность, свободную от влияния ионосферы получают по
формуле:
L12
L22
D 2 2 1 2 2 2 ,
L1 L2 L1 L2
1 и 2 – псевдодальноти, измеренные на частотах L1 и L2
16

17.

Учет влияния вертикальной рефракции
в тригонометрическом нивелировании
Понятие коэффициента рефракции
Коэффициент рефракции k ― отношение радиуса кривизны Земли RЗ к
среднему радиусу кривизны рефракционной кривой ρср:
k
RЗ
ср
RЗ grad ср n
17

18.

Введение поправки за влияние вертикальной рефракции
D2
hr k
2 RЗ
k RЗ grad ср n
RЗ
1
kст
0,14
ср 7
Nikon NPL-632 kст=0,132
Реальный диапазон значений k=±6
Оценка требований
к точности определения коэффициента рефракции
2 RЗ
D2
mh mk
mk mh
2 RЗ
D2
r
r
D2
h k
2 RЗ
r
18