Теория сигналов

1. ТЕОРИЯ СИГНАЛОВ

Презентация лекции по курсу «Общая теория связи»
© Д.т.н., проф. Васюков В.Н., vasyukov@corp.nstu.ru
Новосибирский государственный технический университет,
Новосибирск, пр. К. Маркса, 20
Факультет Радиотехники и электроники
Кафедра теоретических основ радиотехники

2.

Многие вещи нам непонятны не потому,
что наши понятия слабы; но потому, что
сии вещи не входят в круг наших
понятий.
Козьма Прутков. Мысли и афоризмы, № 66
2

3. Модели сигналов

Вообще под моделью понимается некоторый объект
(реальный или воображаемый), который заменяет в
некотором смысле другой объект.
Для нас под этим другим объектом будет подразумеваться
сигнал как физический процесс.
Теоретическое рассмотрение (в противоположность
эксперименту) всегда предполагает использование
моделей.
Например, выражение
A cos(2 ft )
представляет собой модель сигнала (колебания).
Другая модель того же
сигнала – график
1
x( t)
1
0
t
10
3

4. Требования к моделям

адекватность, то есть соответствие модели
реальному объекту (не означает точного совпадения
модели и объекта)
точность, то есть степень близости результатов,
полученных с помощью модели, к известным
(экспериментальным)
простота модели, то есть требуемая точность
результатов должна достигаться при умеренных
трудозатратах
универсальность, то есть применимость модели
для решения многих близких задач
4

5. Необходимость математических моделей

Общий подход к разработке и проектированию
современных технических систем, в том числе
систем связи, заключается в получении
оптимальных или хотя бы субоптимальных
технических решений.
Такие решения, как правило, не могут быть
получены эмпирическим путем, для этого
необходимо располагать соответствующими
теоретическими, т.е. математическими методами.
5

6.

Теория сигналов – математическая теория,
описывающая с единых позиций все
многообразие электрических сигналов,
применяемых в
• проводной и радиосвязи,
• радио- и телевизионном вещании,
• радиолокации и радионавигации,
• автоматике и телемеханике,
• глобальных и локальных
компьютерных сетях и
• во многих других областях техники.
6

7. Математические модели сигналов

Естественно возникает вопрос о способах
математического описания (математических
моделях) сигналов и каналов связи и о
возможностях преобразования различных
моделей друг в друга.
В качестве математических моделей сигналов чаще
всего используются подходящие функции или их
комбинации (суммы и/или произведения функций, их
производных и первообразных и т.п.).
7

8. Модели простейших аналоговых сигналов

Гармоническое колебание
A cos(2 ft )
где
1
x( t)
A - амплитуда,
f - циклическая частота,
1
0
t
10
- начальная фаза.
Вместо косинуса с тем же успехом можно использовать
синус. Кроме того, во многих случаях рассматривается
кóмплексное гармоническое колебание
A exp j (2 ft ) Ae
j (2 ft )
j 1
8

9. Связь гармонических колебаний

Согласно формулам Эйлера
j (2 ft )
A cos(2 ft ) Re Ae
Asin(2 ft ) Im Ae
j (2 ft )
A exp j (2 ft ) A cos(2 ft )
jAsin(2 ft )
9

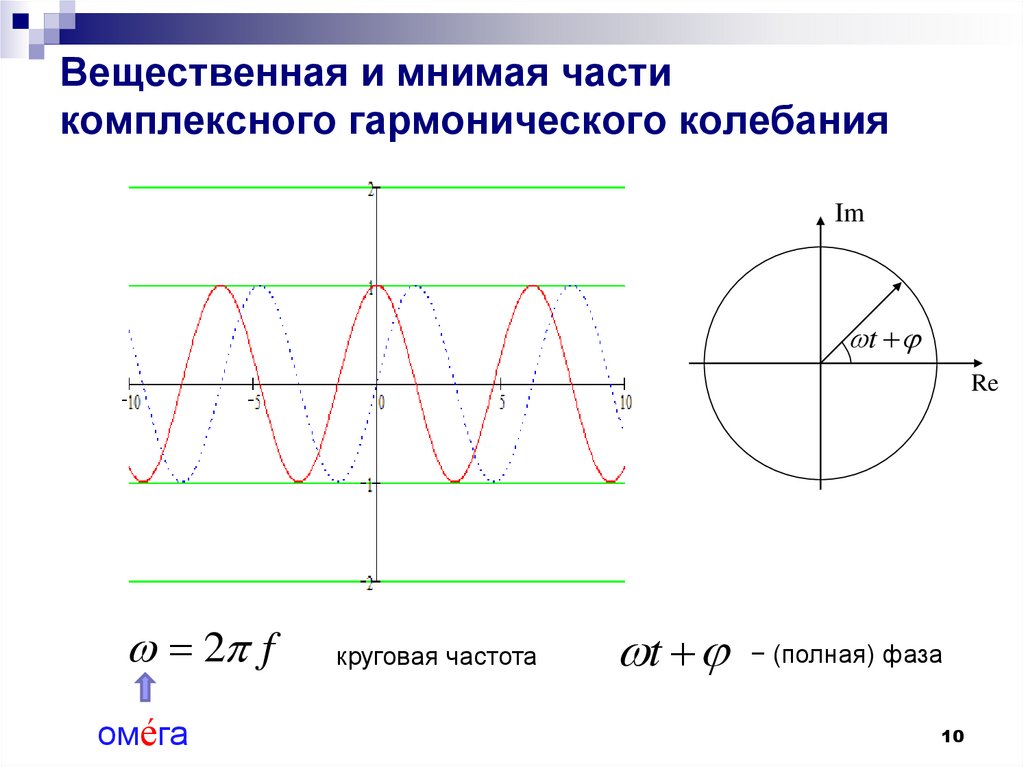
10. Вещественная и мнимая части комплексного гармонического колебания

Im
t
Re
2 f
омéга
круговая частота
t − (полная) фаза
10

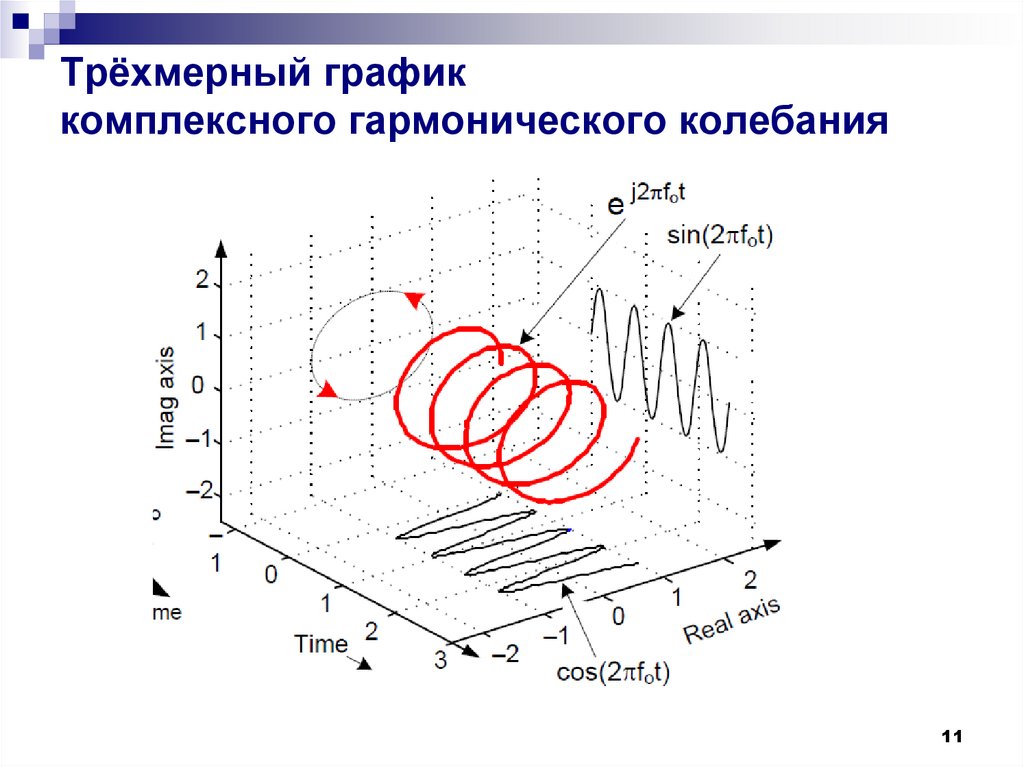
11. Трёхмерный график комплексного гармонического колебания

11

12. Периодические сигналы

Т, что
x(t ) x(t T )
Если существует такое
сигнал периодический
A cos(2 ft ) Re Ae j (2 ft )
Asin(2 ft ) Im Ae
j (2 ft )
A exp j (2 ft ) A cos(2 ft )
jAsin(2 ft )
1
Если к t прибавить k
f
значение функции не изменится
1
T
f
период
12

13. Функция включения Хэвисайда

(t )
1
1 при t 0,
(t ) 0.5 при t 0,
0 при t 0.
0
t
Oliver Heaviside, 1850-1925
Прямоугольный импульс
r (t ) (t и / 2) (t и / 2)
1
r (t )
и / 2 0
и / 2
t
13

14. Дельта-функция Дирака

f (t0 )
f (t ) (t t0 )dt
стробирующее (фильтрующее) свойство
дельта-функции
f (t0 ) lim
1
и 0 и
f (t )r (t t0 )dt
Paul Adrien
Maurice Dirac
(1902-1984)
14

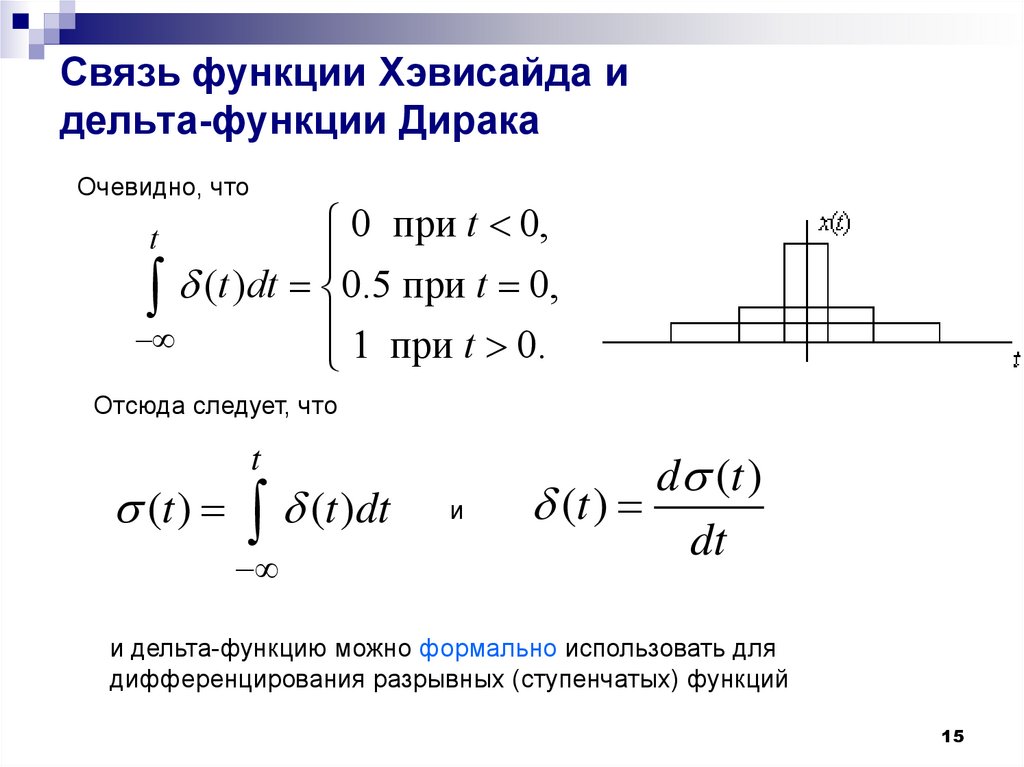
15. Связь функции Хэвисайда и дельта-функции Дирака

Очевидно, что
0 при t 0,
(t )dt 0.5 при t 0,
1 при t 0.
t
Отсюда следует, что
t
(t ) (t )dt
и
d (t )
(t )
dt
и дельта-функцию можно формально использовать для
дифференцирования разрывных (ступенчатых) функций
15

16. Динамическое представление сигналов

Выражение стробирующего (фильтрующего) свойства
x(t0 )
x(t ) (t t0 )dt
можно переписать (с учётом чётности дельта-функции) в виде
x(t )
x( ) (t )d
и понимать как предел
x(n и )
0
x(t ) lim
и
n
r (t n и )
и
и
16

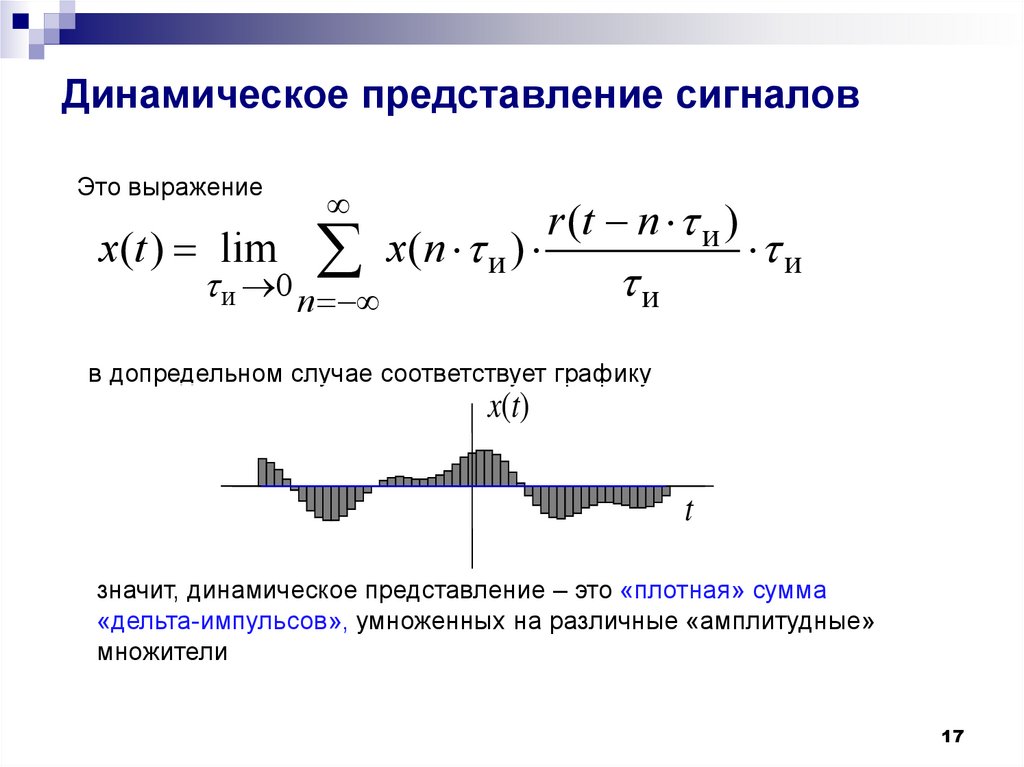
17. Динамическое представление сигналов

Это выражение
x(n и )
0
x(t ) lim
и
n
r (t n и )
и
и
в допредельном случае соответствует графику
x(t)
t
значит, динамическое представление – это «плотная» сумма
«дельта-импульсов», умноженных на различные «амплитудные»
множители
17

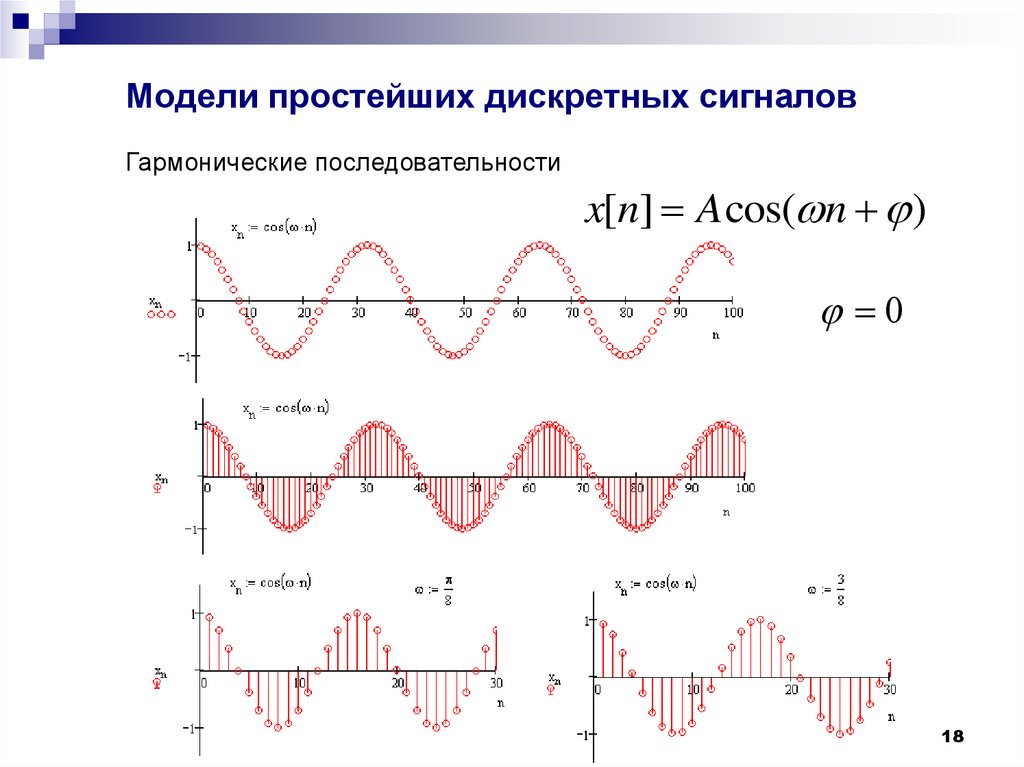
18. Модели простейших дискретных сигналов

Гармонические последовательности
x[n] A cos( n )
0
18

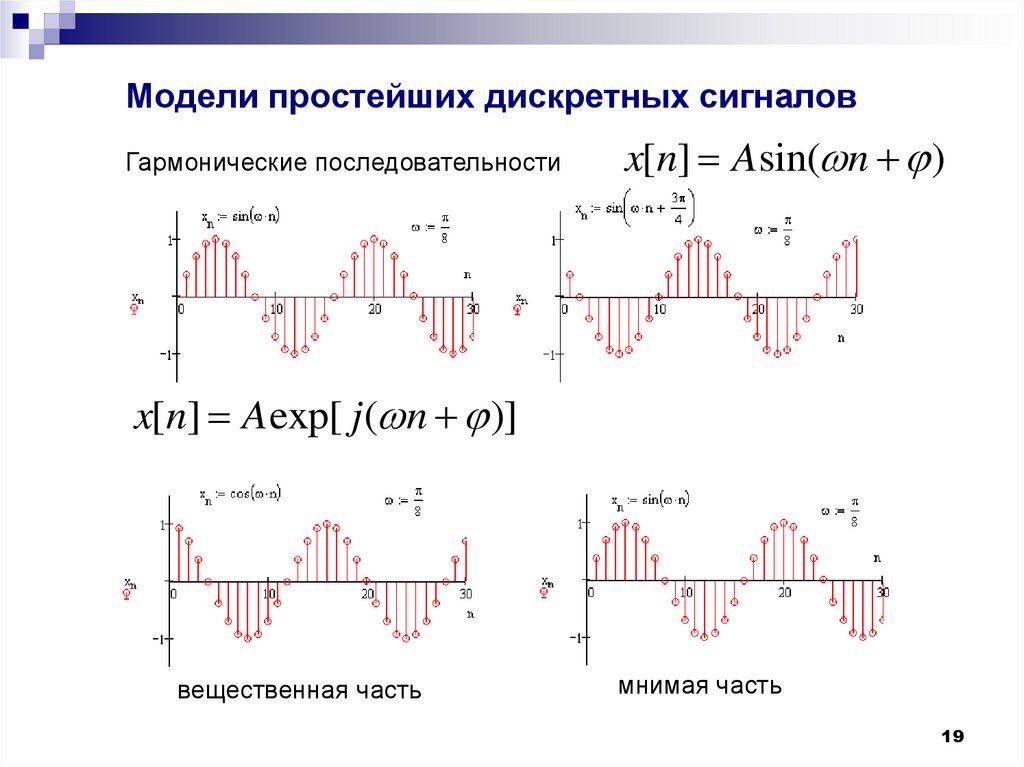
19. Модели простейших дискретных сигналов

Гармонические последовательности
x[n] Asin( n )
x[n] A exp[ j ( n )]
вещественная часть
мнимая часть
19

20. Модели простейших дискретных сигналов

Ступенчатая последовательность
1 при n 0,
u[n]
0 при n 0.
1
0
n
0
n
Дельта-последовательность (единичная
последовательность, «единичный импульс»)
1, n 0,
[ n]
0, n 0,
1
их взаимосвязь:
n
u[n] [k ]
k
[n] u[n] u[n 1]
20

21. Модели простейших дискретных сигналов

Очевидные соотношения
n
u[n] [k ]
[n] u[n] u[n 1]
и
k
соответствуют выражениям для функций Хэвисайда и Дирака
t
(t ) (t )dt
и
d (t )
(t )
dt
Заметим: производным соответствуют (конечные) разности;
дифференциальным уравнениям – разностные уравнения
21

22. Представление дискретных сигналов суммой сдвинутых дельта-последовательностей

Выражение, аналогичное динамическому
представлению аналогового сигнала
x[n] x[k ] [n k ]
k
соответствует просто взвешенной сумме дельтапоследовательностей, сдвинутых на целое число шагов
Очевидно, так можно представить ЛЮБОЙ дискретный
сигнал, так же, как динамическое представление
справедливо для ЛЮБОГО аналогового (континуального)
сигнала
Однако во многих случаях удобнее оказываются иные модели…
22

23. Современные модели сигналов

Представление сигнала в виде графика описывающей его
функции является наглядным и привычным.
23

24.

Принцип действия осциллографа
24

25.

Временнóе представление не является, однако, ни
единственным, ни самым лучшим. На практике при
решении конкретных задач следует выбирать наиболее
удобные формы описания сигналов.
Основное неудобство временного представления сигналов:
сигналу соответствует сложный объект (функция,
изображаемая графиком) в простом пространстве (на
плоскости).
В современной теории сигналов используется
представление сигнала простым объектом (точкой) в
сложном пространстве.
Это пространство представляет собой множество
всевозможных сигналов, рассматриваемых в данной
задаче, наделённое соответствующими структурными
свойствами
25

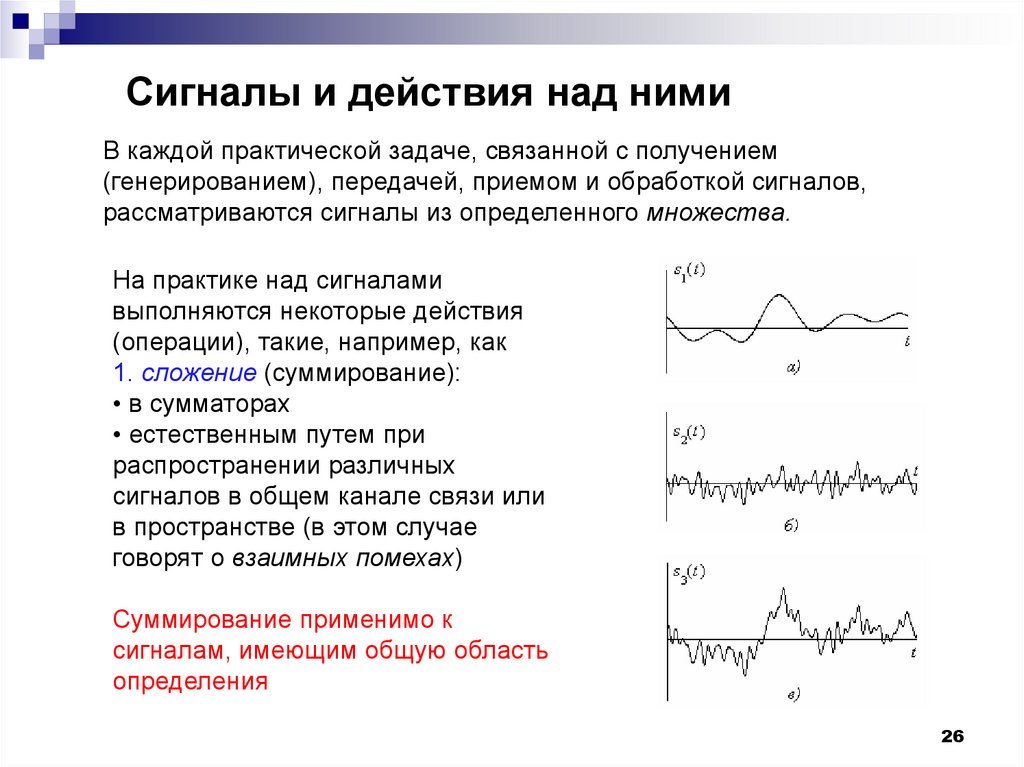
26. Сигналы и действия над ними

В каждой практической задаче, связанной с получением
(генерированием), передачей, приемом и обработкой сигналов,
рассматриваются сигналы из определенного множества.
На практике над сигналами
выполняются некоторые действия
(операции), такие, например, как
1. сложение (суммирование):
• в сумматорах
• естественным путем при
распространении различных
сигналов в общем канале связи или
в пространстве (в этом случае
говорят о взаимных помехах)
Суммирование применимо к
сигналам, имеющим общую область
определения
26

27. Сигналы и действия над ними

2. умножение сигнала на некоторый постоянный коэффициент:
• множитель больше единицы – усиление сигнала при помощи
усилителей
• меньше единицы – ослабление естественное или
преднамеренное с помощью аттенюатора
• множитель может быть и отрицательным, тогда меняется
полярность сигнала, а соответствующее устройство называют
инвертирующим усилителем, или инвертором
27

28. Сходство сигналов с векторами

Сумма двух сигналов – сигнал
Сумма двух векторов – вектор
Сигнал, умноженный на скаляр – сигнал
Вектор, умноженный на скаляр – вектор
замкнутость относительно
сложения
замкнутость относительно
умножения на скаляр
линейное пространство – модель для множества сигналов,
которое становится пространством сигналов
28

29. Представление сигналов векторами

Рассмотрим для примера множество дискретных сигналов, таких,
что все значения (отсчеты) этих сигналов равны нулю, за
исключением значений, соответствующих
n 2
n 1
и
Пусть
x[1] x1
и
x[2] x2
Конкретный сигнал из
этого множества – вектор
на плоскости, а всё
множество сигналов –
это множество точек
плоскости, т.е вся
плоскость
29

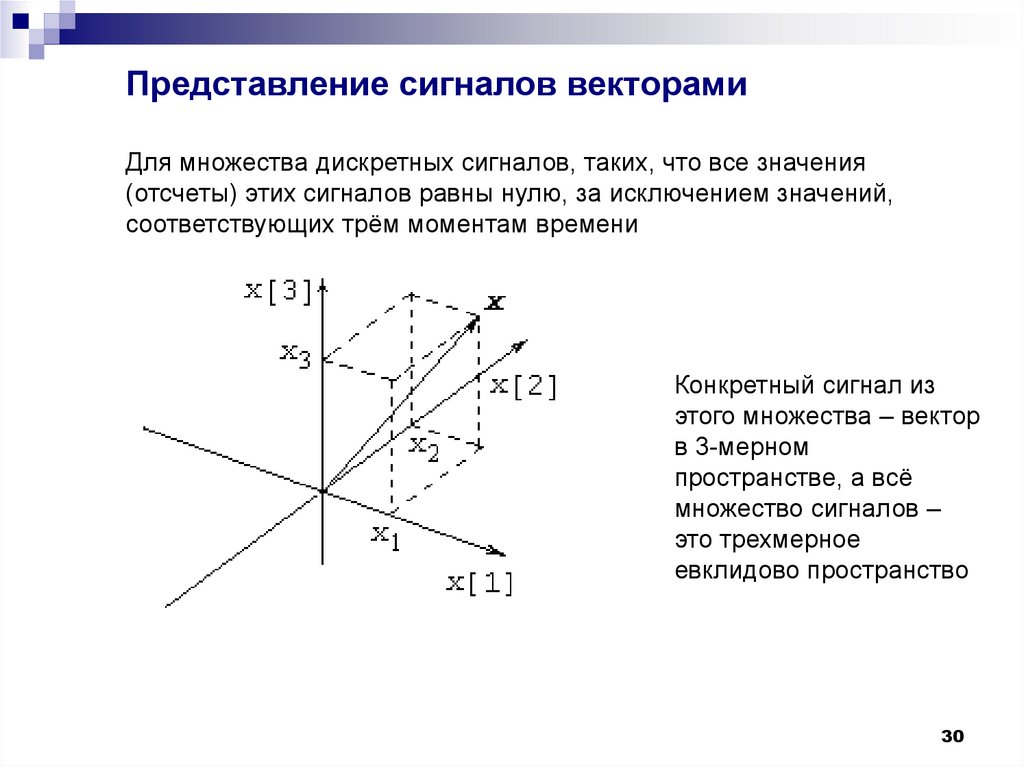
30. Представление сигналов векторами

Для множества дискретных сигналов, таких, что все значения
(отсчеты) этих сигналов равны нулю, за исключением значений,
соответствующих трём моментам времени
Конкретный сигнал из
этого множества – вектор
в 3-мерном
пространстве, а всё
множество сигналов –
это трехмерное
евклидово пространство
30

31. Представление сигналов векторами

Множество всех сигналов, определяемых их значениями в
конечном множестве N точек дискретной временнóй оси
представляется множеством векторов N-мерного евклидова
пространства.
Бесконечномерное евклидово пространство, пригодное для
представления всех дискретных сигналов, определенных на
бесконечной целочисленной временнóй оси
получается при N
Это пространство имеет бесконечное, но счетное
множество «координатных осей».
Континуальным сигналам соответствует
бесконечномерное пространство с несчетным
множеством (континуумом) «координатных осей»
31

32. Линейное пространство

Линейным пространством называется множество объектов (векторов),
удовлетворяющее следующим аксиомам:
А. Определена операция сложения, множество замкнуто
относительно сложения: x M y M : ( x y ) M
а1. ассоциативность x, y, z M :
x ( y z ) ( x y) z
а2. существование нейтрального элемента (нулевого вектора)
0 M : x M : x 0 x
а3. существование противоположного элемента
x M ( x) M : x ( x) 0
а4. коммутативность
x, y M : x y y x
а1…а3 – группа; а1…а4 – коммутативная (áбелева) группа
(Niels Henrik Abel; 1802—1829)
32

33.

Б. C множеством М векторов связано другое множество F скаляров,
и определена операция умножения вектора на скаляр:
x M F : x M
замкнутость по умножению
б1. ассоциативность
( x) ( ) x x x M , F
б2. существование в поле скаляров особого элемента – единицы
1 F : x M :1x x
б3. дистрибутивность сложения векторов и умножения вектора
на скаляр
( x y ) x y x, y M F ,
(правила
раскрытия скобок)
(
)
x
x
x
x
M
,
F.
.
Все эти аксиомы выполняются для сигналов, как аналоговых, так и
дискретных – вещественных и комплексных. Поэтому
сигналы можно рассматривать как векторы и называть векторами.
33

34. Пространства сигналов (примеры)

Пространство всех аналоговых сигналов, определенных на всей
вещественной (временной) оси: L или L ,
Пространство аналоговых сигналов ограниченной энергии,
заданных на бесконечной временной оси, которое принято
обозначать L ,
или просто L2
2
Пространство сигналов ограниченной энергии, определенных на
данном конечном временнóм интервале (сигналы конечной
длительности, тождественно равные нулю вне интервала) L2 (T )
Пространство сигналов с ограниченной полосой частот
L2 ( F )
Пространство всех дискретных сигналов ограниченной
энергии, заданных на всей дискретной временной оси l2 , l2
,
l2 ,
L2 ( F )
ЦОС
34