дфз3 - копия

1.

ОБРАБОТКА РЕЗУЛЬТАТОВ ОТСЕИВАЮЩИХ
ЭКСПЕРИМЕНТОВ
При проведении экспериментальных исследований
возникает два противоречивых стремления:
1. Упростить процесс исследований, сократив число
опытов, что даже в процессе активного эксперимента
возможно лишь при исследовании минимального числа
факторов;
2. Получить в результате экспериментальных
исследований максимум информации и наиболее полные
сведения об исследуемом объекте, не опустив при этом
из рассмотрения ни одного существенного фактора.
Стремление понятное и его можно реализовать, но
лишь проведением двухэтапных исследований
105

2.

ДИСПЕРСИОННЫЙ АНАЛИЗ
Р. ФИШЕР, 1920
Основная задача ДА:
• Оценить влияние каждого из факторов и их комбинаций на
выходной параметр, (выделить из всего многообразия
факторов, воздействующих на процесс, лишь те, влияние
которых наиболее существенно)
Суть дисперсионного анализа:
Если на выходной параметр У действуют взаимно независимые
факторы х1, х2, …, хn , то общую дисперсию выходного
параметра Dу можно представить в виде суммы дисперсий,
обусловленных отдельными факторами и их комбинациями:
Dy = Dх1 + Dх2 + Dх1х2 + … + Dхn
106

3.

Анализируя составляющие общей дисперсии, можно оценить
вклад каждого из исследуемых факторов на выходной
параметр.
Однако, чтобы точно оценить дисперсии отдельных факторов
необходимо измерить их на нескольких уровнях ;
Для оценки остаточной дисперсии, характеризующей разброс
величины выходного параметра, необходим многократный
дубляж опытов (не думайте, что это повторное измерение
выходного параметра в опытах);
Т.о. Для проведения ДА необходимо иметь большой объём
экспериментального материала (Вы уже поняли, что это очень
трудоёмкий процесс?);
Изучаемые факторы должны быть независимыми;
Выходной параметр должен иметь НОРМАЛЬНОЕ
распределение.
ИТАК, ВАМ СТАНОВИТСЯ ЯСНЫМ, ПОЧЕМУ МЫ НЕ БУДЕМ
ЗАНИМАТЬСЯ ДИСПЕРСИОННЫМ АНАЛИЗОМ.
107

4.

МЕТОД СЛУЧАЙНОГО БАЛАНСА
САТТЕРЭВАЙТ, 1956 г.
Используется для выявления количественных
факторов, оказывающих существенное влияние на
выходной параметр, т.е. ДОМИНИРУЮЩИХ
ФАКТОРОВ
Метод пригоден для активного эксперимента, т.е. в
ходе его имеется возможность изменять выходные
параметры по определённому плану
При планировании отсеивающего эксперимента
используют матрицу ПФЭ или ДФЭ, выбирая из неё
случайным образом определённое число опытов
Полученная матрица отсеивающего эксперимента
является СЛУЧАЙНО СБАЛАНСИРОВАННОЙ
108

5.

ПРИМЕР
По данным дробного факторного эксперимента,
представляющего собой 1/16 реплики от полного факторного
эксперимента типа 27, оценить влияние на механическую
скорость бурения (у, м/ ч) следующих СЕМИ факторов:
•Нагрузки на долото (х1,тс);
•Частоты вращения ротора ( х2, об/мин);
•Интенсивности промывки (расхода бурового раствора) (х3, л/с);
•Условной вязкости бурового раствора (х4, с) ;
•Показателя фильтрации бурового раствора (х5, см3/30- мин);
•Диаметра насадки гидромониторного долота (х6, мм) ;
•Плотности бурового раствора (х7, кг/м3).
УРОВНИ ФАКТОРОВ ПРИВЕДЕНЫ В ТАБЛ.1, А РЕЗУЛЬТАТЫ ОПЫТОВ В
ТАБЛ. 2
109

6.

Таблица 1.
УРОВЕНЬ
ЗНАЧЕНИЕ ФАКТОРА
х1
х2
х3
х4
х5
х6
х7
Верхний (+1)
18
120
36
45
12
14
1260
Нижний (-1)
10
60
24
25
4
190
1200
Для визуального выделения доминирующих факторов
по результатам эксперимента строят ДИАГРАММЫ
РАССЕЯНИЯ, число которых равно числу факторов.
В качестве иллюстрации рассмотрим построение
диафрагмы рассеяния для фактора х1.
110

7.

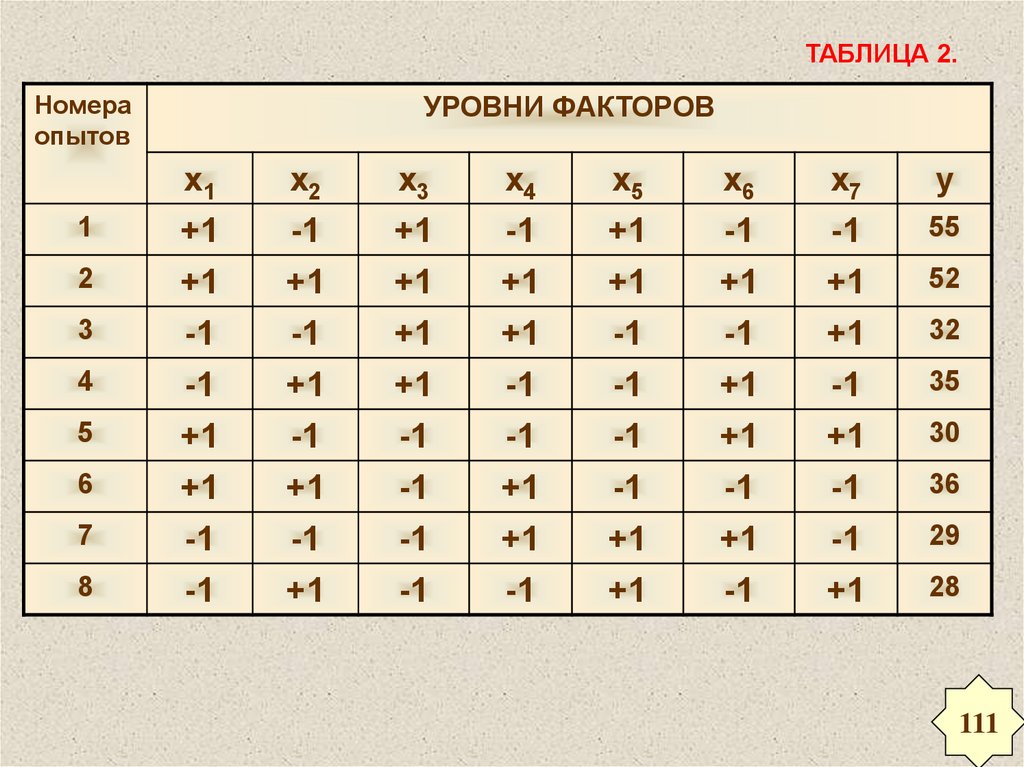
ТАБЛИЦА 2.
Номера
опытов
1
2
3
4
5
6
7
8
УРОВНИ ФАКТОРОВ
х1
х2
х3
х4
х5
х6
х7
у
+1
+1
-1
-1
+1
-1
+1
+1
+1
-1
+1
+1
+1
+1
-1
-1
+1
-1
-1
+1
+1
55
-1
+1
+1
+1
-1
+1
+1
-1
-1
-1
-1
+1
-1
-1
-1
+1
+1
-1
-1
+1
-1
35
-1
-1
-1
+1
-1
-1
+1
-1
+1
+1
+1
-1
-1
+1
29
52
32
30
36
28
111

8.

1. Определим средние значения выходного
параметра У в опытах, когда фактор х1 находится
на нижнем (-1) и верхнем (+1) уровнях:
1
y x1 1 32 35 29 28 31
4
1
y x1 1 55 52 30 36 43.25
4
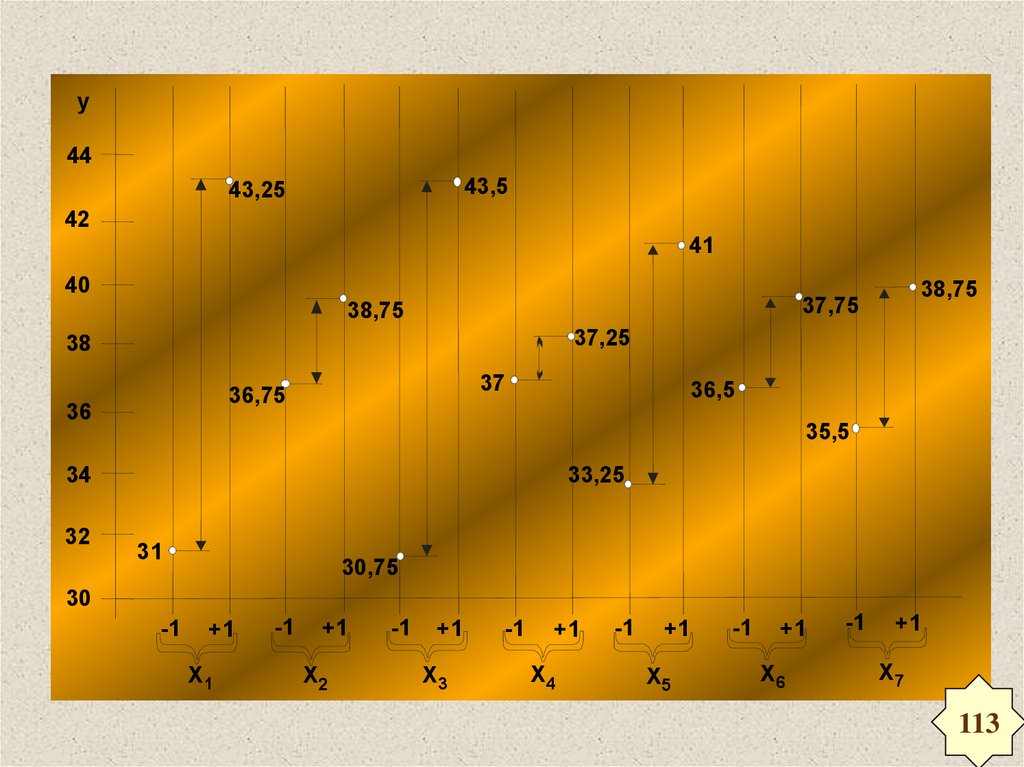
2. По полученным данным в масштабе построим
диаграмму рассеяния для фактора х1
112

9.

у
44
43,5
43,25
42
41
40
38,75
37,25
38
37
36,75
36
36,5
35,5
34
32
38,75
37,75
33,25
31
30,75
30
-1
+1
Х1
-1
+1
Х2
-1
+1
Х3
-1
+1
Х4
-1
+1
Х5
-1
+1
Х6
-1
+1
Х7
113

10.

Аналогично строятся диаграммы рассеяния для
других факторов
Расстояние, обозначенное стрелками,
характеризует различия между средними
значениями выходного параметра на 2-х уровнях
рассматриваемого фактора и ПОКАЗЫВАЕТ
насколько существенно он влияет на величину
выходного параметра (чем больше расстояние, тем
больше влияние).
Сравнивая расстояния на диаграммах рассеяния
располагают их в порядке снижения влияния на
механическую скорость: х3, х1, х5, х7, х2,х6, х4.
При этом: х2,х6, х4 могут быть признаны как
незначимые (не оказывающие на выходной
параметр у существенного влияния).
114