Similar presentations:
Развёртывание поверхностей
1.
Лекция 11РАЗВЁРТЫВАНИЕ
ПОВЕРХНОСТЕЙ
Красовская Н.И.
2.
Общие понятияи определения
Красовская Н.И.
3.
Развёрткой поверхностиназывают плоскую фигуру, полученную при
совмещении развёртываемой поверхности с
плоскостью
При этом поверхность рассматривают как
гибкую, нерастяжимую пленку
Красовская Н.И.
4.
Развёртываниемназывают такое преобразование поверхности,
в результате которого она совмещается с
плоскостью
Красовская Н.И.
5.
Поверхность развёртываемая,если между точками поверхности и развёртки
можно установить взаимно-однозначное
соответствие, при котором сохраняются
длины линий, расположенных на
поверхности, величины углов между линиями
и площади фигур, ограниченных этими
линиями
Красовская Н.И.
6.
Поверхность неразвёртываемая,если между точками поверхности и развёртки
нельзя установить взаимно-однозначное
соответствие
Красовская Н.И.
7.
Условные развертки неразвертываемойповерхности - развертка развертываемой
поверхности, которой приближенно, но практически
допустимо, можно заменить (аппроксимировать)
данную неразвертываемую поверхность
Красовская Н.И.
8.
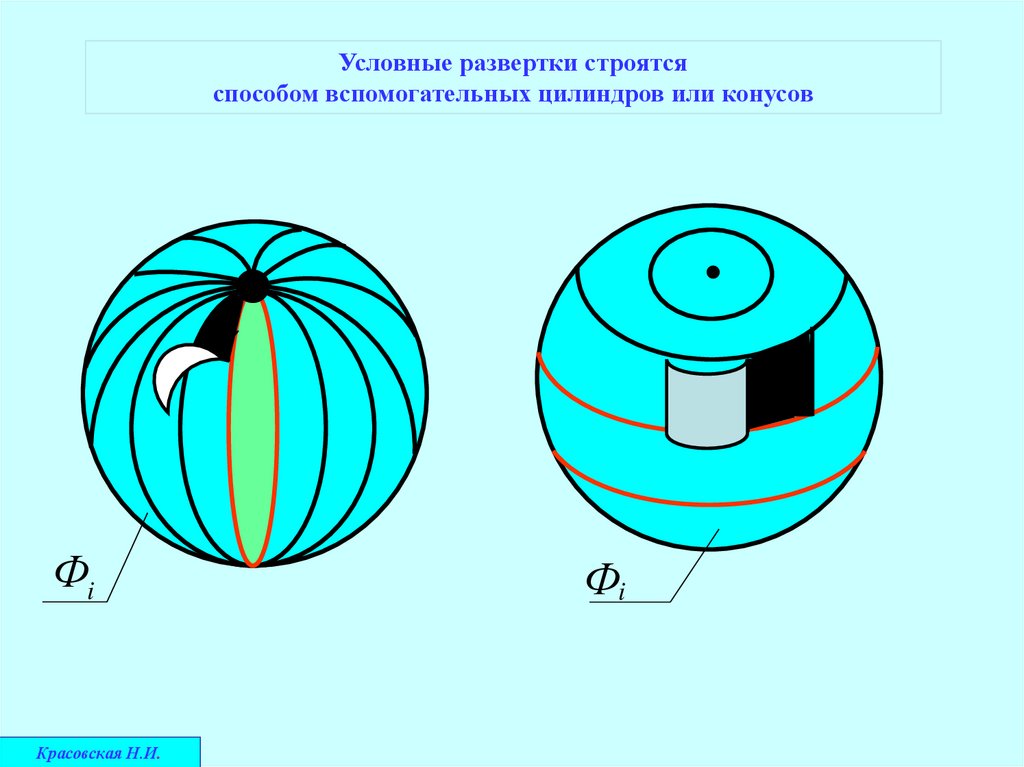
Условные развертки строятсяспособом вспомогательных цилиндров или конусов
Фi
Красовская Н.И.
Фi
9.
Основные свойстваразвёрток
поверхностей
Красовская Н.И.
10.
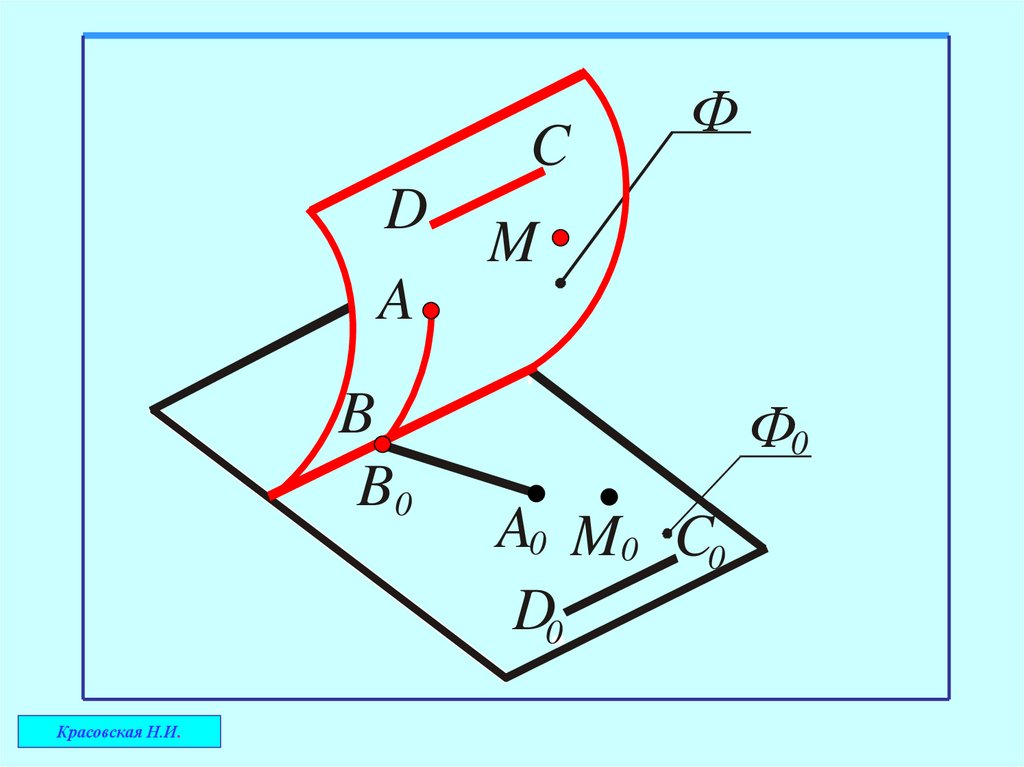
1. Каждой точке поверхности соответствуетединственная точка на её развёртке и наоборот
2. Каждой линии на поверхности соответствует
линия на развёртке поверхности
Длины линий на поверхности и развёртке равны
между собой
Красовская Н.И.
11.
CD
Ф
M
A
B
B0
Красовская Н.И.
Ф0
A0 M0 C0
D0
12.
3.Параллельным линиям на поверхностисоответствуют параллельные линии на
развёртке
4.Замкнутая линия на поверхности и
соответствующая ей линия на развёртке
ограничивают одинаковые площади
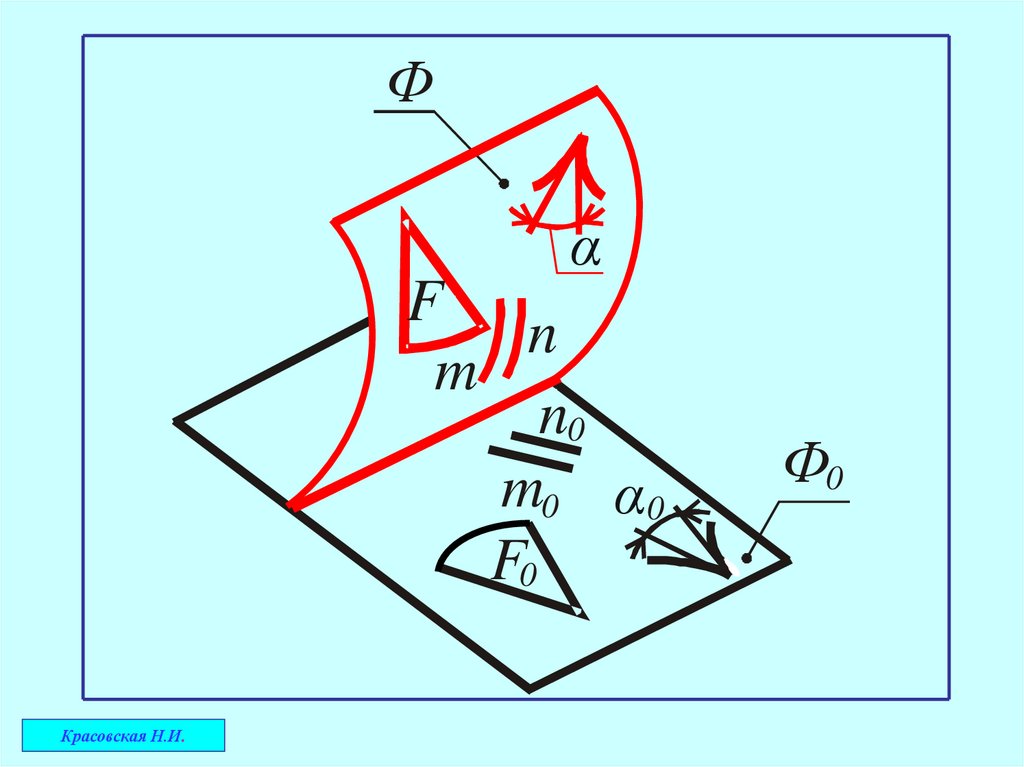
5.Угол между линиями на поверхности
равен углу между соответствующими линиями
на развёртке
(угол между кривыми линиями находится как угол между касательными к кривым
линиям в точке их пересечения)
Красовская Н.И.
13.
Фα
F
n
m
n0
m0 α 0
F0
Красовская Н.И.
Ф0
14.
Развёртки прямых круговыхконусов
и цилиндров
Красовская Н.И.
15.
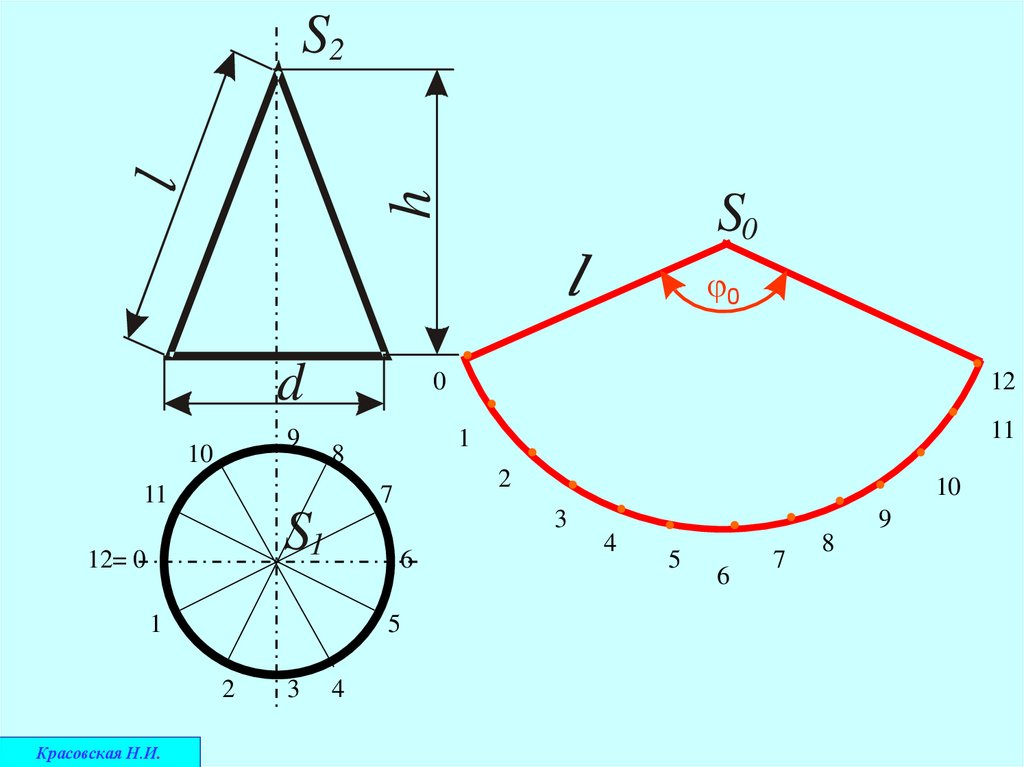
Развёртка боковой поверхности конуса вращенияпредставляет собой
круговой сектор,
радиус которого равен длине образующей конуса l, а
центральный угол φ0 определяется по формуле
180d
0
l
Красовская Н.И.
16.
hS2
S0
0
d
9
10
0
6
1
5
2
3
10
3
S1
Красовская Н.И.
2
7
12= 0
11
1
8
11
12
4
9
4
5
6
7
8
17.
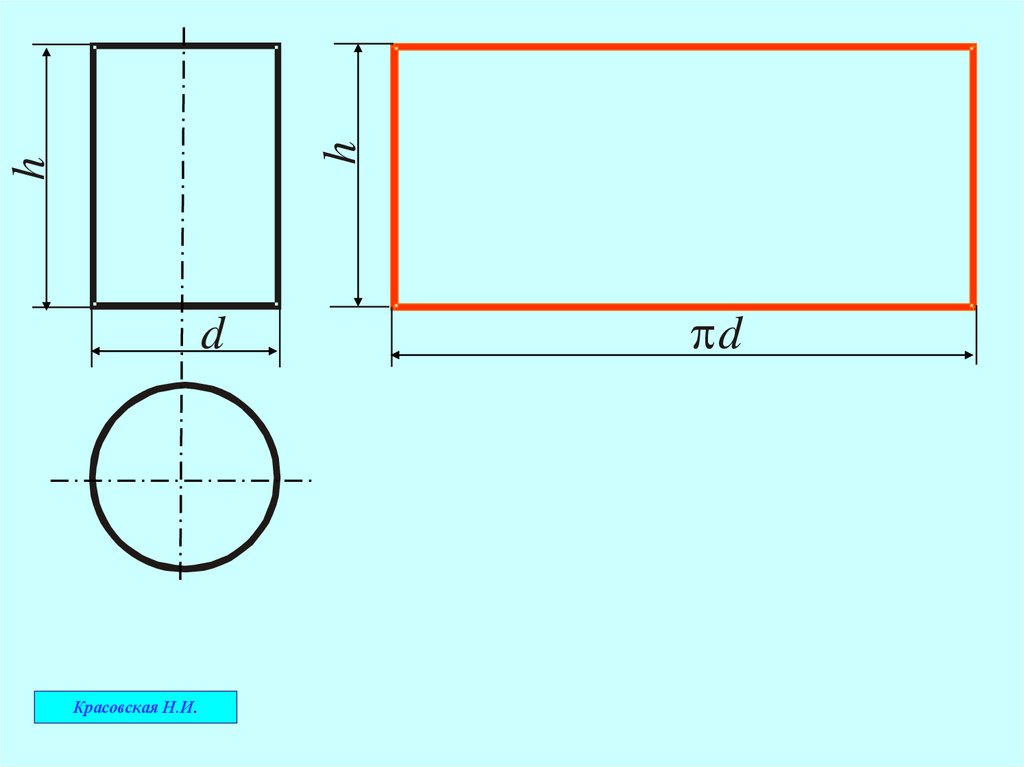
Развёртка боковой поверхности прямого круговогоцилиндра представляет собой прямоугольник,
одна из сторон которого равна длине окружности
основания Πd,
а другая − высоте цилиндра h
Красовская Н.И.
18.
hh
d
Красовская Н.И.
pd
19.
Способы построенияразвёрток
Красовская Н.И.
20.
При построении развёрток используютследующие способы:
─ способ триангуляции
(треугольников);
─ способ нормального сечения
и др.
Красовская Н.И.
21.
Способтриангуляции
Красовская Н.И.
22.
Алгоритмрешения задачи
на построение развёртки
конической поверхности
Красовская Н.И.
23.
Алгоритм включает в себя этапаппроксимации
конической поверхности пирамидальной
Красовская Н.И.
24.
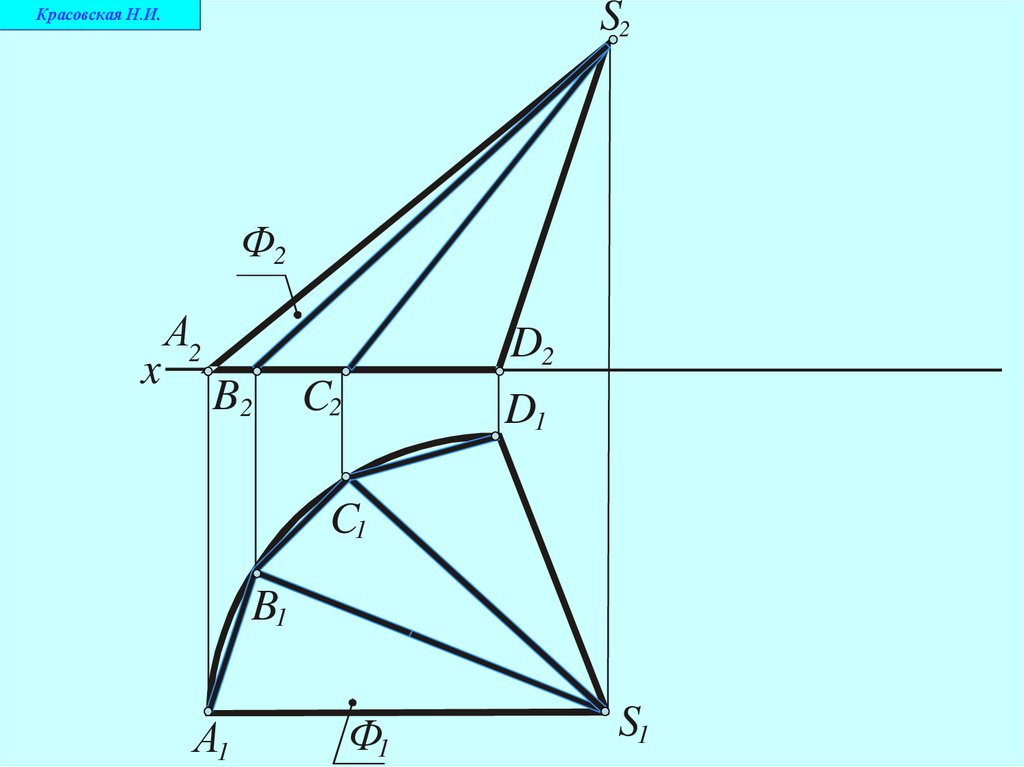
1. В данную поверхность вписываетсяпирамидальная поверхность
25.
S2Красовская Н.И.
Ф2
x
А2
D2
B2
C2
D1
C1
B1
А1
Ф1
S1
26.
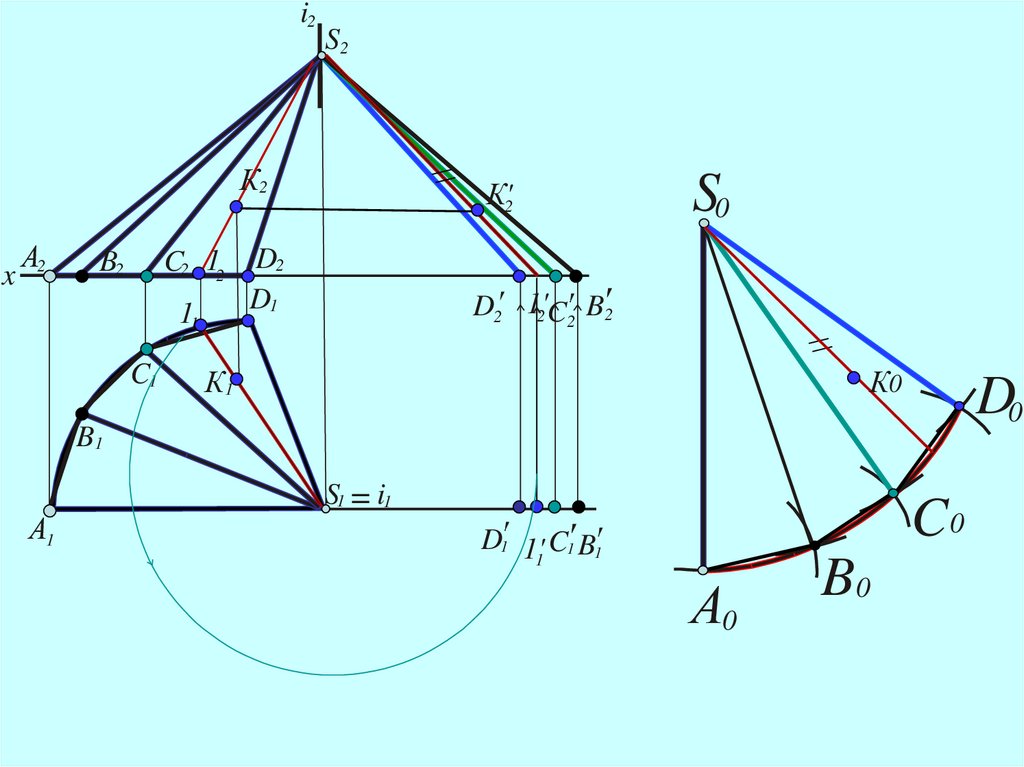
2. Определяются натуральные величины всех реберпирамидальной поверхности
3. На свободном поле чертежа с помощью циркуля
строятся примыкающие друг к другу треугольники с
общей вершиной S0 , стороны которых являются
ребрами пирамиды в натуральную величину
4. Точки основания соединяются плавной кривой линией
Красовская Н.И.
27.
i2S2
Н.В.
Н.В.
S0
x
А2
B2
C2
D2
D1
D2 C2
B2
C1 Н.В.
Н.В.
B1
Н.В.
А1
D0
S1 = i1
C0
D1 C1 B1
А0
B0
28.
i2S2
К2
x
А2
C2 12
B2
11
C1
S0
К'2
D2
D1
D2 1'2 C2 B2
К1
К0
D0
B1
А1
S1 = i1
C0
D1 1' C1 B1
1
А0
B0
29.
Способнормального
сечения
Красовская Н.И.
30.
Алгоритмрешения задачи
на построение развёртки
призматической поверхности
Красовская Н.И.
31.
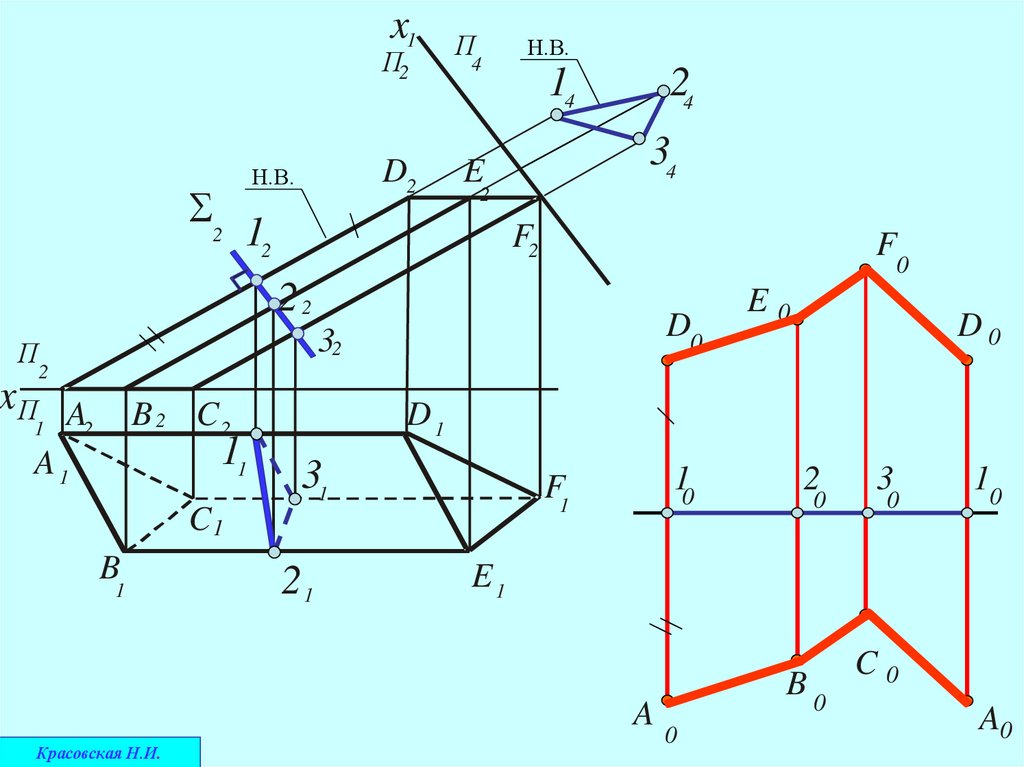
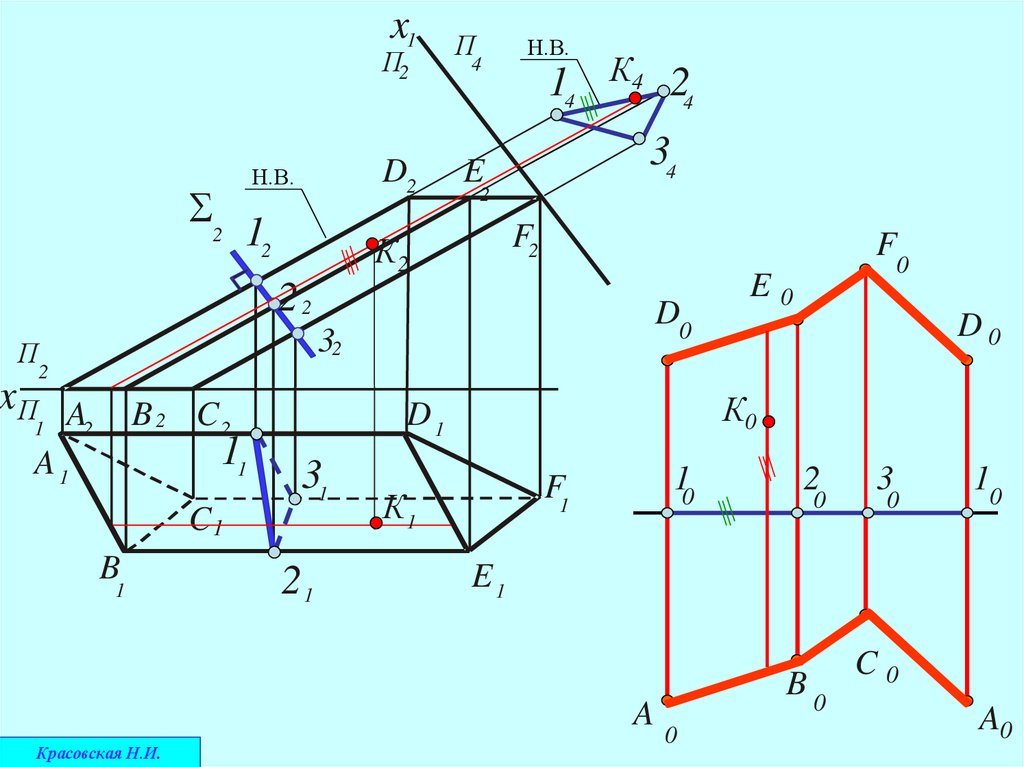
1. Задается секущая плоскость перпендикулярно образующим (ребрам)призматической поверхности
2. Строится фигура сечения
3. Определяется натуральная величина фигуры, полученной в сечении
4. Натуральная величина линии нормального сечения разворачивается в
прямую линию
5.Через опорные точки перпендикулярно к развернутой линии строятся
образующие (рёбра) поверхности в натуральную величину
Концы образующих соединяются отрезками прямых
Красовская Н.И.
32.
x1П2
S2
D2
Н.В.
П
4
Н.В.
14
24
34
E
2
12
F2
F
0
22
D0
32
П
E0
D0
2
xП A
1
B 2 C2
2
11
A1
D1
31
C1
B
1
21
10
F1
0
3
0
10
E1
A
Красовская Н.И.
2
B0
0
C0
A0
33.
x1П2
S2
D2
Н.В.
12
П
4
Н.В.
14 К4 24
34
E
2
F2
К2
F
22
D0
32
П
0
E0
D0
2
xП A
1
B 2 C2
2
11
A1
31
C1
B
1
К0
D1
21
10
F1
К1
0
3
0
10
E1
A
Красовская Н.И.
2
B0
0
C0
A0
34.
Условные развёрткинеразвёртываемых
поверхностей
Красовская Н.И.
35.
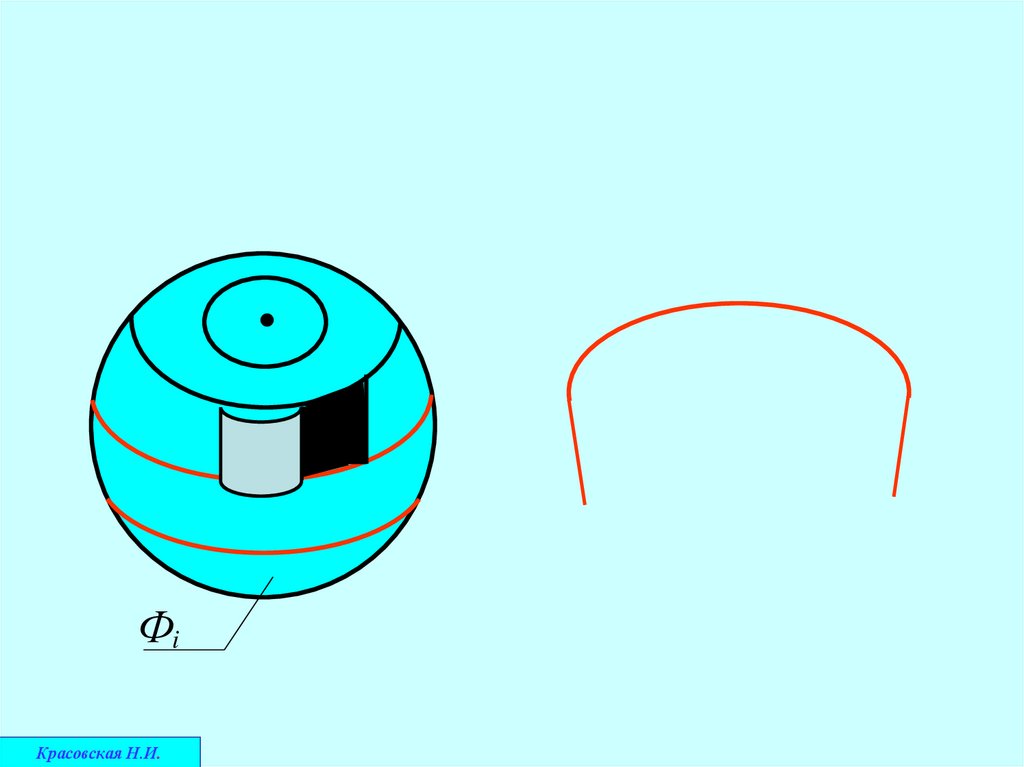
1. Исходя из требуемой точности развёртки, данную поверхностьФ разрезают на несколько равных или примерно равных отсеков –
Фi
2. Выполняют приближенные развёртки отсеков поверхностей
Фi0, аппроксимируя их отсеками развёртываемых поверхностей
Совокупность развёрток отсеков принимается
за условную развёртку данной поверхности
Красовская Н.И.
36.
ФiКрасовская Н.И.
37.
ФiКрасовская Н.И.
38.
Построениеусловной развертки сферы
способом вспомогательных
цилиндров
Красовская Н.И.
39.
1.С помощью вертикальных плоскостей, проходящих через центрсферы, разбивают ее поверхность на восемь равных отсеков
2.Попарно противоположные отсеки аппроксимируют
цилиндрической поверхностью
(цилиндр, описанный вокруг сферы)
3.Строят развертку отсека, заключенного между смежными
меридиональными сечениями
Красовская Н.И.
40.
Алгоритмпостроения развертки отсека
цилиндрической поверхности
Красовская Н.И.
41.
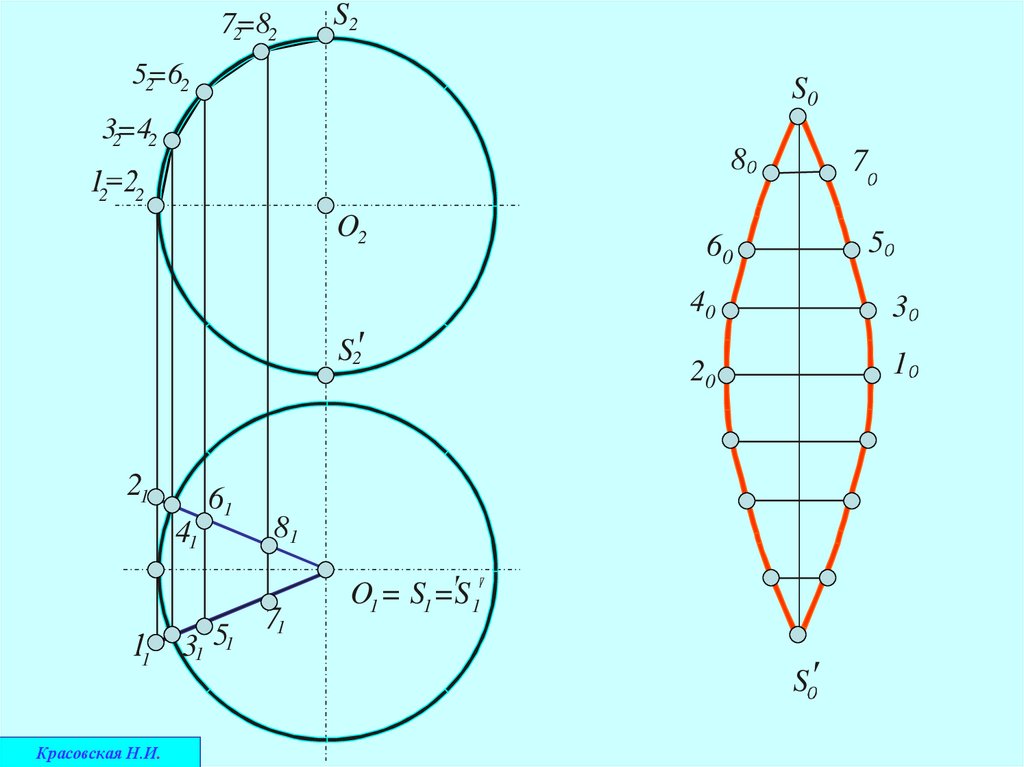
1.Проводят в пределах отсека несколько переменных образующих−горизонтальных отрезков
Эти образующие проецируются на горизонтальную плоскость проекций в
натуральную величину, а расстояния между ними проецируются
в натуральную величину на фронтальную плоскость проекций в виде
соответствующих дуг окружностей
2. На вертикальной прямой откладывают отрезки, равные расстояниям
между образующими отсека.
Полученный отрезок равен длине полумеридиана
3.Через соответствующие точки делений проводят горизонтальные
отрезки, равные длинам образующих отсека цилиндрической поверхности
4.Соединив плавной кривой концы образующих, получают развертку
одного отсека
Восемь подобных разверток и составят условную развертку сферы
Красовская Н.И.
42.
7=82 2
S2
5=6
2 2
S0
3=4
2 2
2
8
7
2
O2
S2
21
61
41
1
Красовская Н.И.
31 51
5
60
40
3
20
1
81
71
O1 = S1 =S 1
S
43.
Способвспомогательных
конусов
Красовская Н.И.
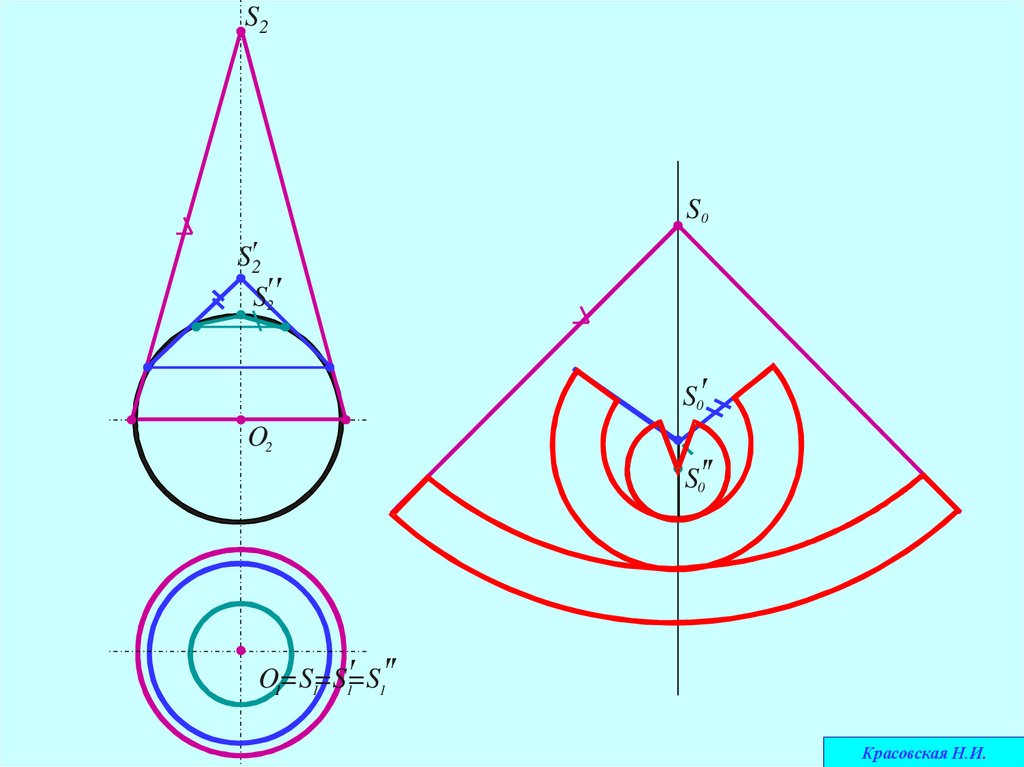
44.
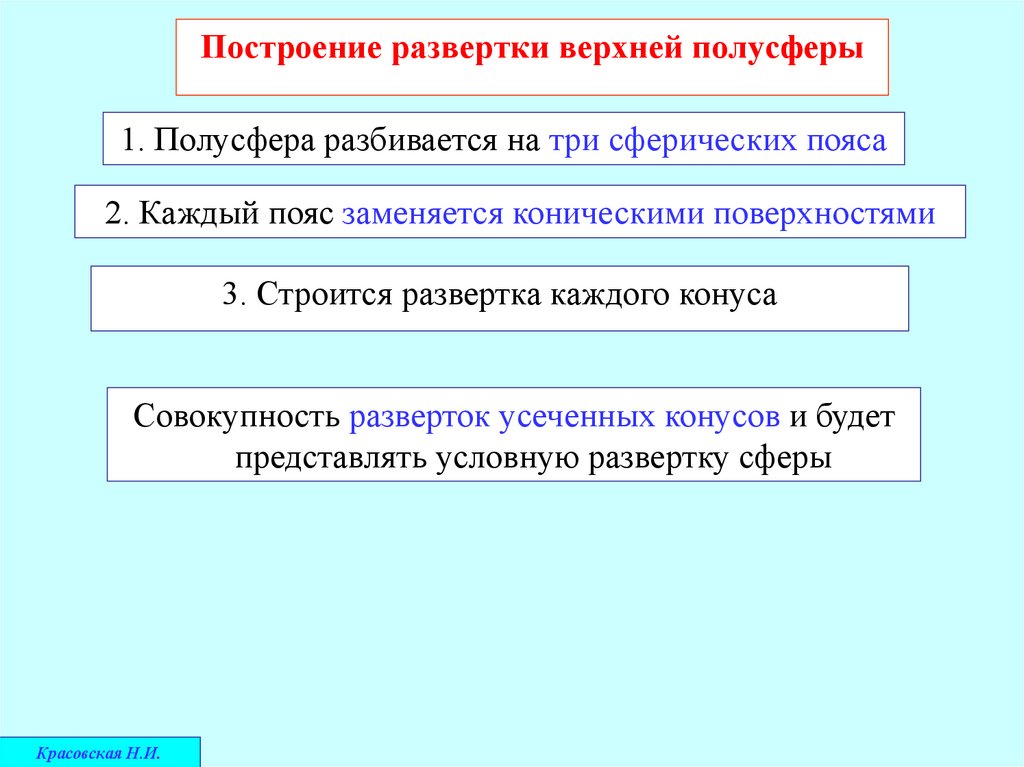
Построение развертки верхней полусферы1. Полусфера разбивается на три сферических пояса
2. Каждый пояс заменяется коническими поверхностями
3. Строится развертка каждого конуса
Совокупность разверток усеченных конусов и будет
представлять условную развертку сферы
Красовская Н.И.
45.
S2S0
S2
S2
S0
O2
S0
O=S=S=S
1
1
1
1
Красовская Н.И.
46.
Выводы- развертки могут быть точными,
приближенными и условными
- между точками поверхности и развертки
существует взаимно-однозначное соответствие
Красовская Н.И.
47.
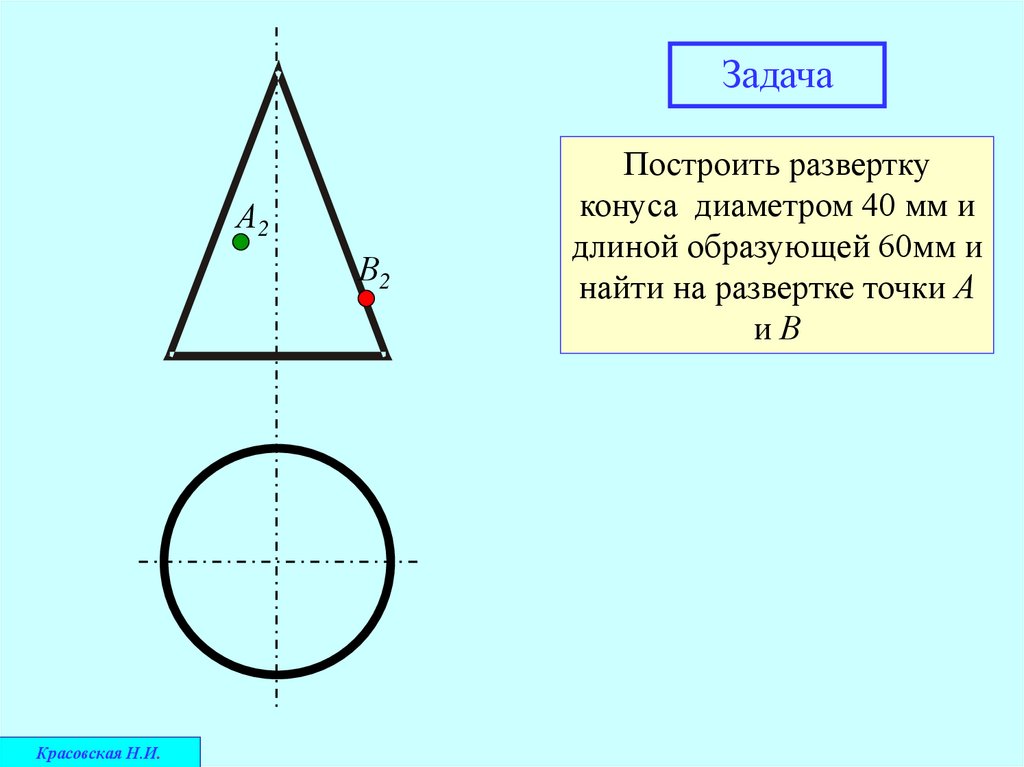
ЗадачаА2
В2
Красовская Н.И.
Построить развертку
конуса диаметром 40 мм и
длиной образующей 60мм и
найти на развертке точки А
иВ

































 mathematics
mathematics








