Логарифмическая_функция,_её_свойства_и_график_

1.

Функция y = log x,
её свойства и график.
a
1

2.

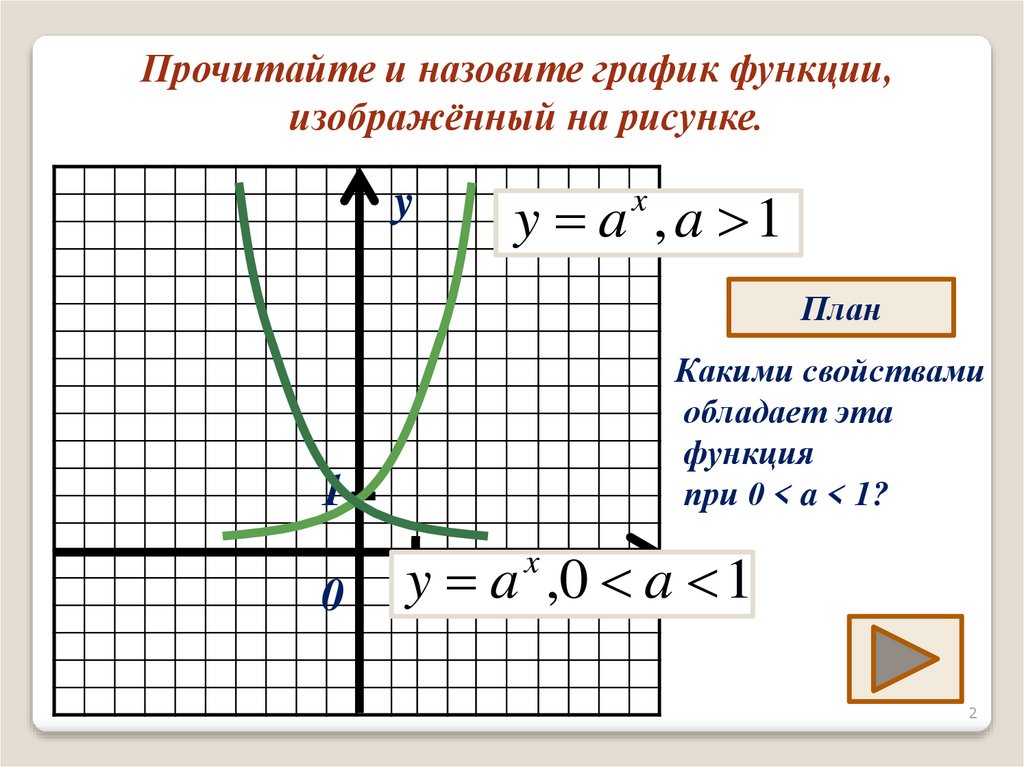
Прочитайте и назовите график функции,
изображённый на рисунке.
y
y a ,a 1
x
План
Какими свойствами
обладает эта
функция
при 0 < a < 1?
1
0
y1 a ,0 xa 1
x
2

3.

План прочтения графика:
1) D(f) – область определения функции.
2) Чётность или нечётность функции.
3) Промежутки возрастания, убывания функции.
4) Ограниченность функции.
5) Наибольшие, наименьшие значения функции.
6) Непрерывность функции.
7) E(f) – область значений функции.
3

4.

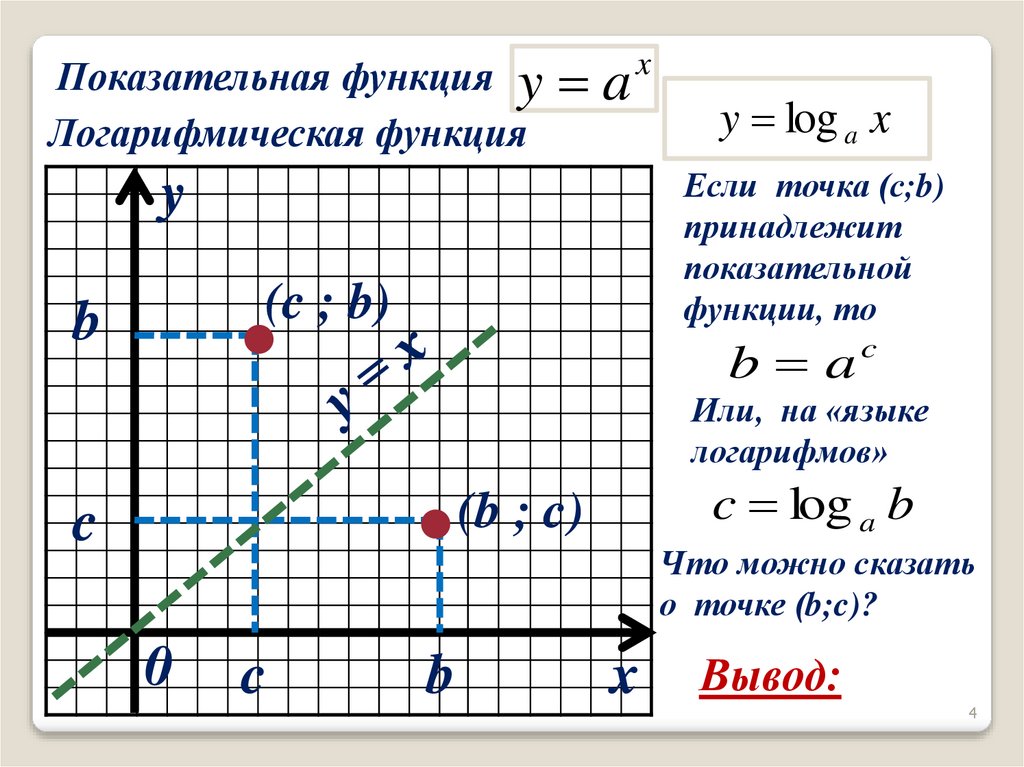
Показательная функция y a x
Логарифмическая функция
Если точка (с;b)
принадлежит
показательной
функции, то
y
(c ; b)
b
y log a x
b a
c
Или, на «языке
логарифмов»
c log a b
(b ; c)
c
Что можно сказать
о точке (b;c)?
0
c
b
x
Вывод:
4

5.

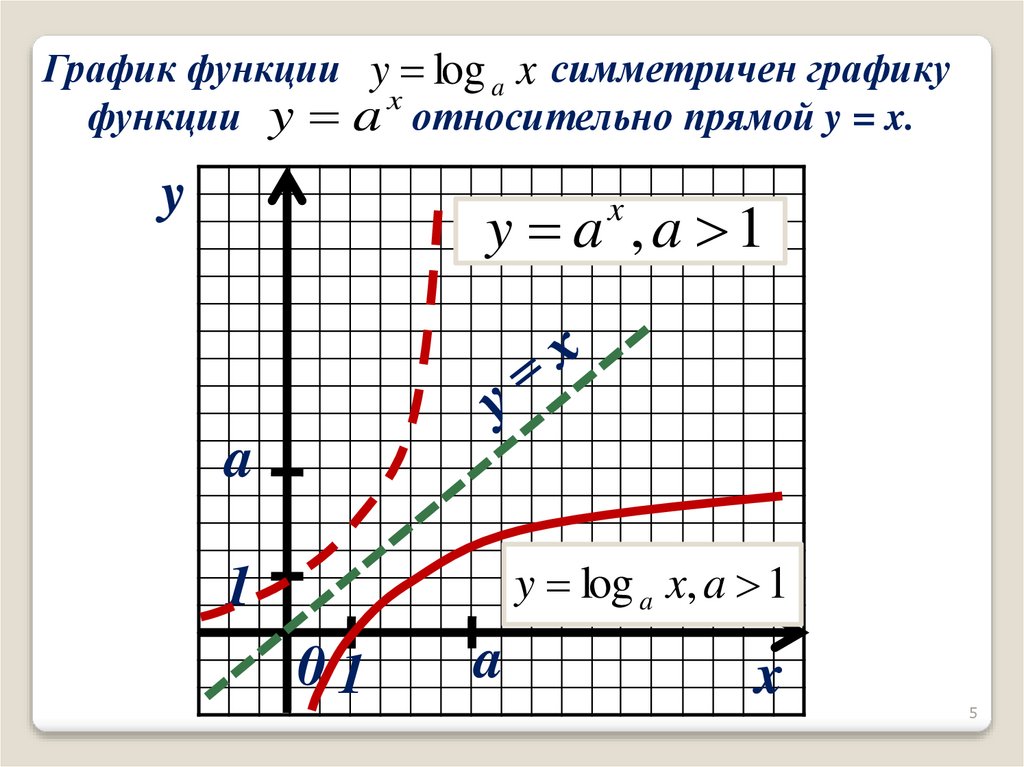
График функции y log a x симметричен графику
x
функции y a относительно прямой y = x.
y
y a ,a 1
x
a
y log a x, a 1
1
01
a
x
5

6.

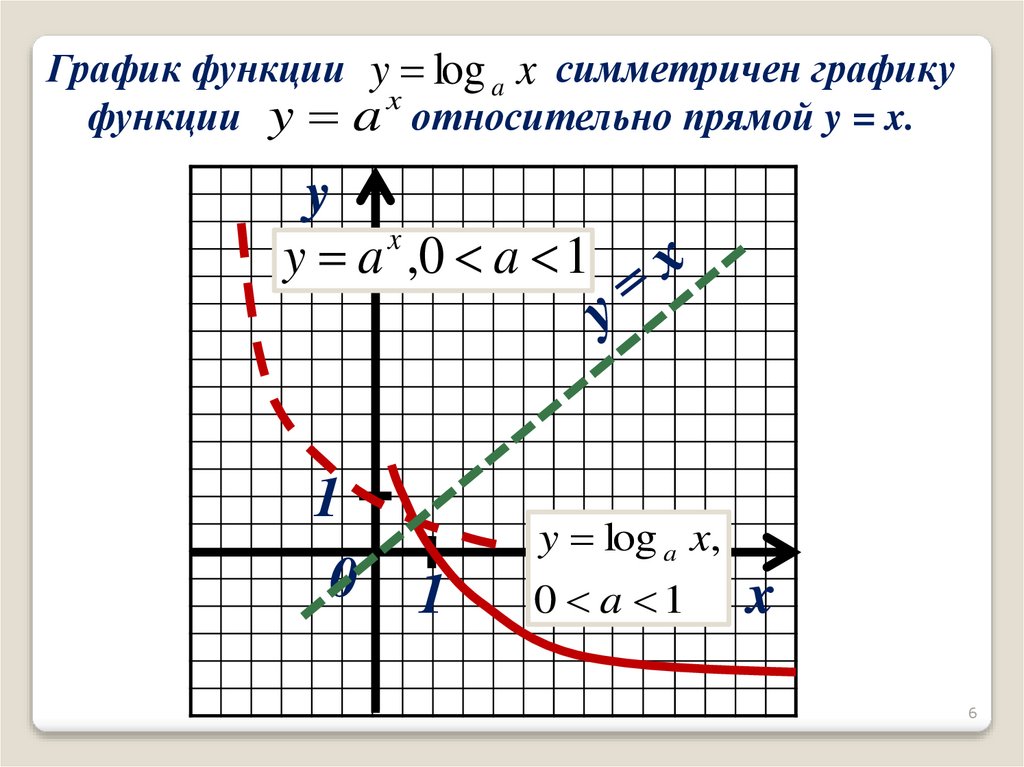
График функции y log a x симметричен графику
x
функции y a относительно прямой y = x.
y
y a ,0 a 1
x
1
0
y log a x,
1
0 a 1
x
6

7.

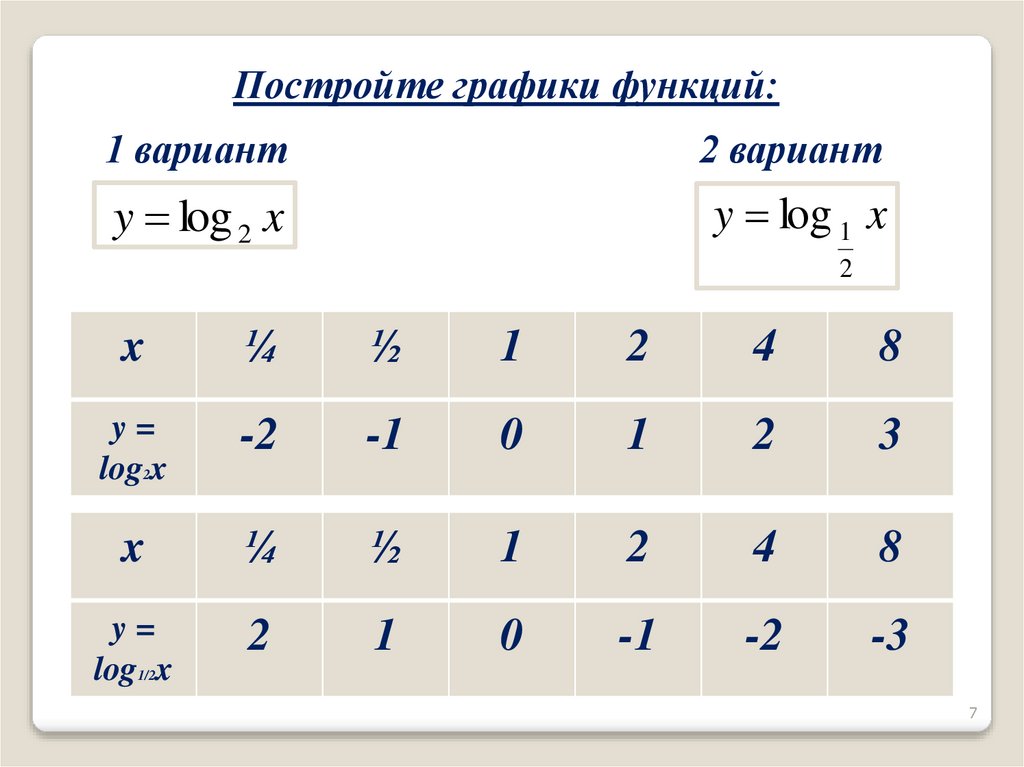
Постройте графики функций:
1 вариант
2 вариант
y log 2 x
y log 1 x
2
x
¼
½
1
2
4
8
y=
log2x
-2
-1
0
1
2
3
x
¼
½
1
2
4
8
y=
log1/2x
2
1
0
-1
-2
-3
7

8.

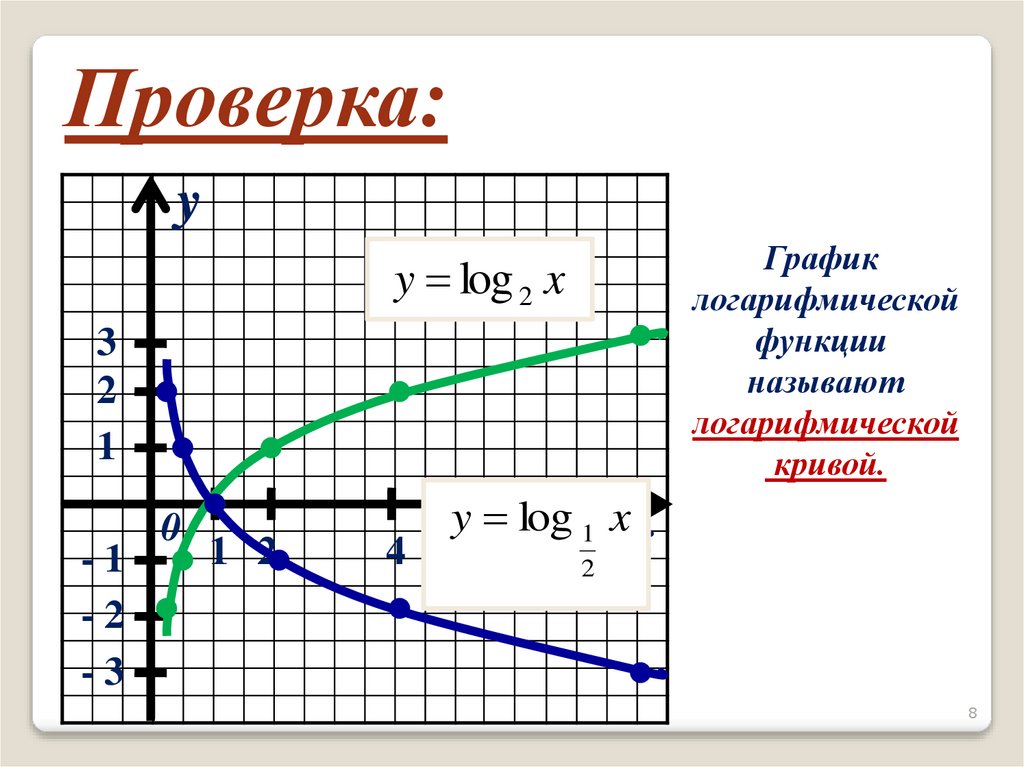
Проверка:
y
График
логарифмической
функции
называют
логарифмической
кривой.
y log 2 x
3
2
1
-1
-2
-3
0
1 2
4
y log 1 x
x
8
2
8

9.

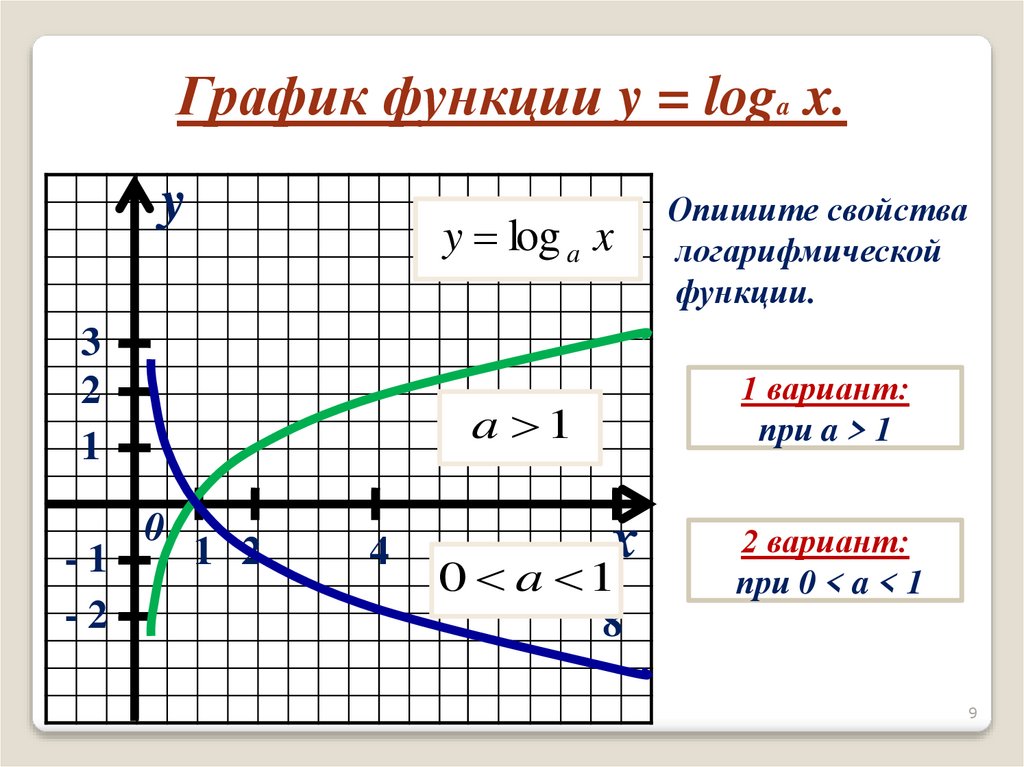
График функции y = loga x.
y
3
2
1
-1
-2
0
1 2
4
y log a x
Опишите свойства
логарифмической
функции.
a 1
1 вариант:
при a > 1
x
0 a 1
2 вариант:
при 0 < a < 1
8
9

10.

Свойства функции у = loga x, a > 1.
у
y log a x
1) D(f) = (0, + ∞);
2) не является ни чётной,
ни нечётной;
0
х
3) возрастает на (0, + ∞);
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
10

11.

Свойства функции у = loga x, 0 < a < 1.
у
1) D(f) = (0, + ∞);
y log a x
2) не является ни чётной,
ни нечётной;
х
0
3) убывает на (0, + ∞);
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
11

12.

Основные свойства логарифмической
функции
№
a>1
0<a<1
1
D(f) = (0, + ∞)
2
не является ни чётной, ни нечётной;
3
возрастает на (0, + ∞)
убывает на (0, + ∞)
4
не ограничена сверху, не ограничена снизу
5
не имеет ни наибольшего, ни наименьшего
значений
6
непрерывна
7
E(f) = (- ∞, + ∞)
12

13.

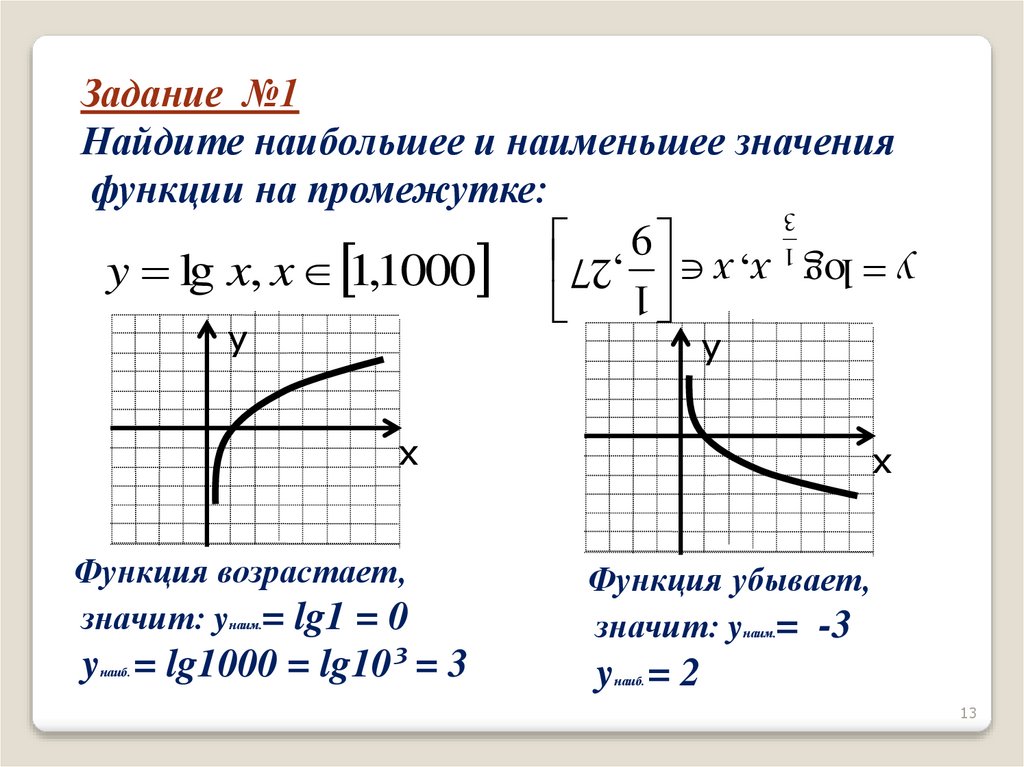
Задание №1
Найдите наибольшее и наименьшее значения
функции на промежутке:
1
y log x, x ,27
9
у
1
3
y lg x, x 1,1000
у
х
х
Функция возрастает,
значит: y = lg1 = 0
Функция убывает,
значит: y = -3
y = lg1000 = lg10³ = 3
y =2
наим.
наиб.
наим.
наиб.
13

14.

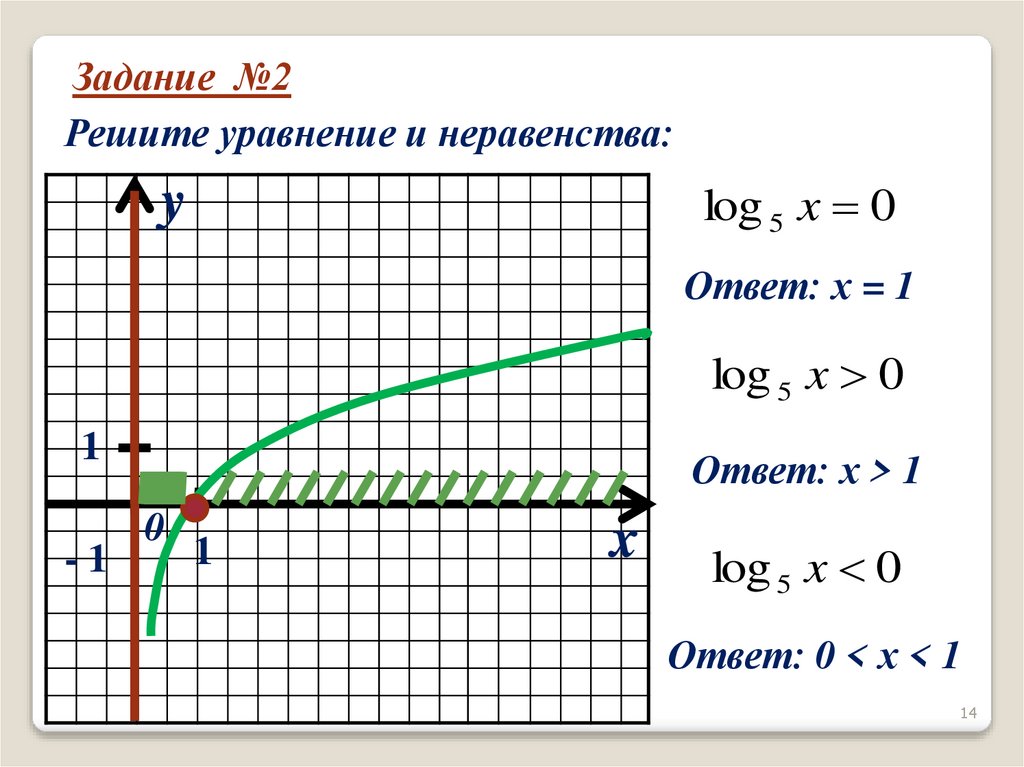
Задание №2
Решите уравнение и неравенства:
log 5 x 0
y
Ответ: х = 1
log 5 x 0
1
-1
Ответ: х > 1
0
1
x
log 5 x 0
Ответ: 0 < х < 1
14

15.

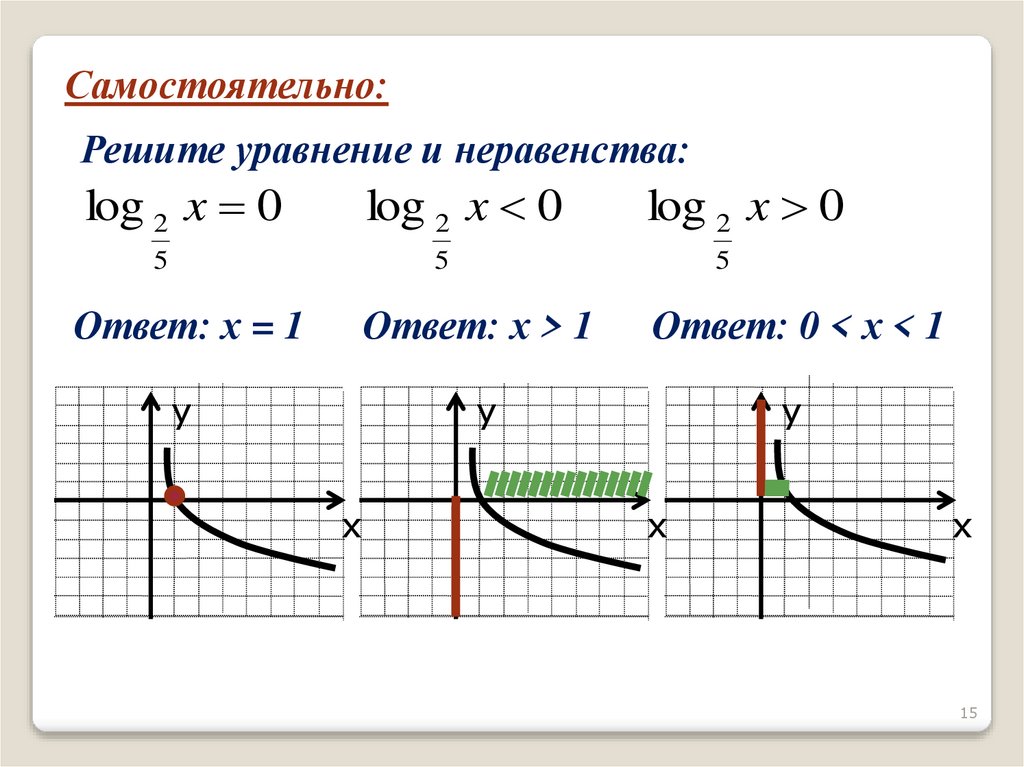
Самостоятельно:
Решите уравнение и неравенства:
log 2 x 0
log 2 x 0
5
log 2 x 0
5
5
Ответ: х = 1
Ответ: х > 1
Ответ: 0 < х < 1
у
у
у
х
х
х
15

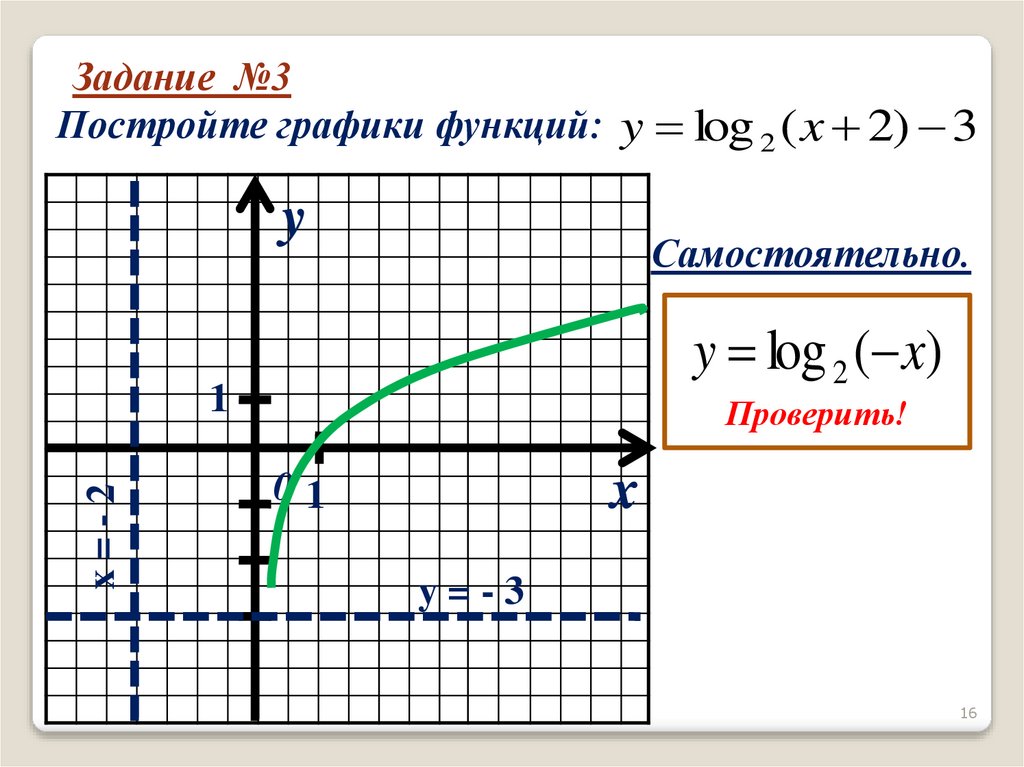
16.

Задание №3
Постройте графики функций: y log 2 ( x 2) 3
y
Самостоятельно.
y log 2 ( x)
x=-2
1
Проверить!
x
01
y=-3
16

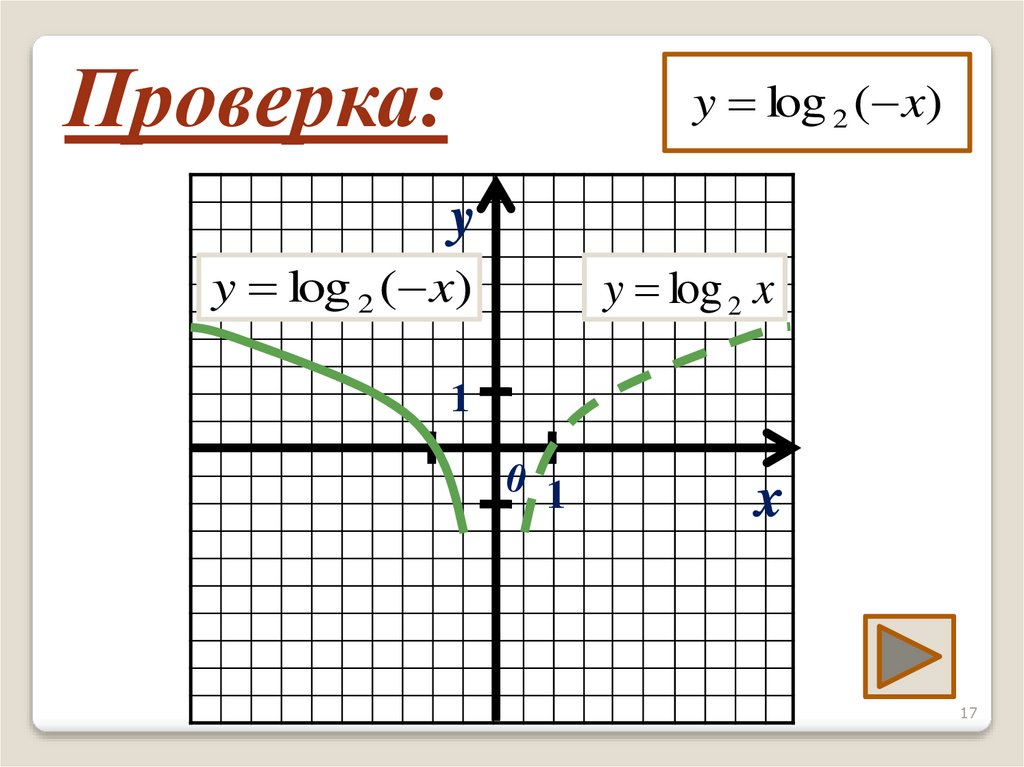
17.

Проверка:
y log 2 ( x)
y
y log 2 ( x)
y log 2 x
1
0 1
x
17