однотонный вариант_Презентация_22.12.24._Формула Гаусса или метод шнуровки (1)

1.

Новогодняя
шнуровка

2.

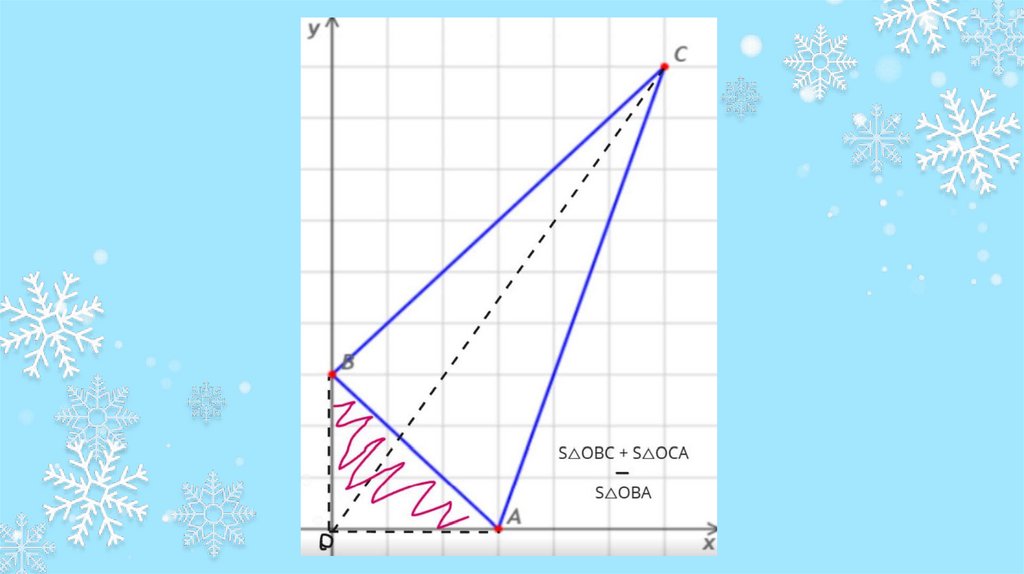
Метод шнуровки Гаусса
(формула площади Гаусса или формула
шнурования или формула землемера) —
это формула определения площади
простого многоугольника, вершины
которого заданы декартовыми
координатами на плоскости.
Она называется формулой шнурования,
так как положительные и отрицательные
слагаемые, состоящие из перемножаемых
координат, располагаются крест-накрест,
как при завязывании шнурков.
Иоганн Карл Фридрих Гаусс (1777—1855) —
немецкий математик, механик, физик, астроном и
геодезист.

3.

Сама формула имеет следующий вид:
Выглядит сложно, не правда ли?

4.

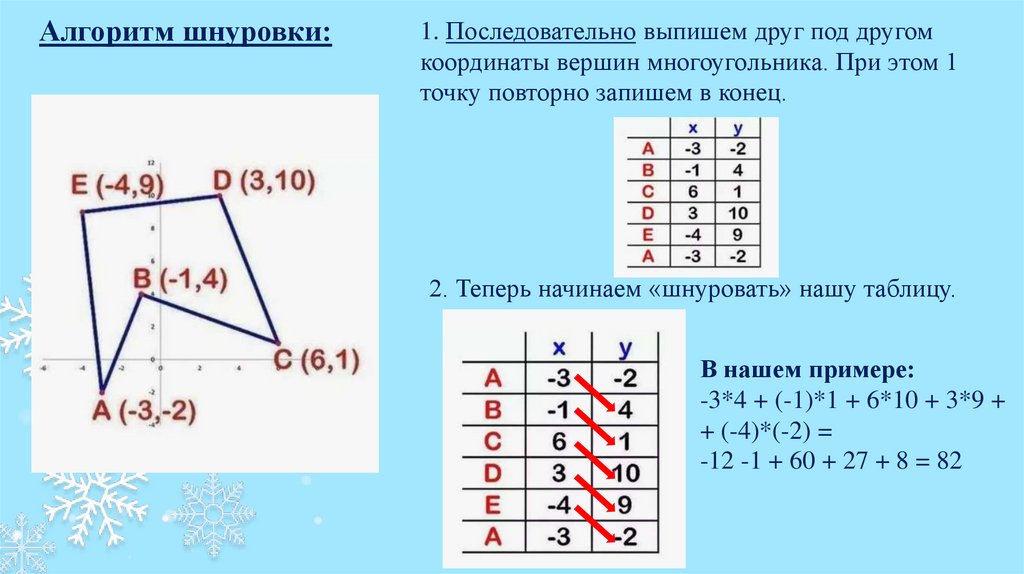
Алгоритм шнуровки:
1. Последовательно выпишем друг под другом
координаты вершин многоугольника. При этом 1
точку повторно запишем в конец.
2. Теперь начинаем «шнуровать» нашу таблицу.
В нашем примере:
-3*4 + (-1)*1 + 6*10 + 3*9 +
+ (-4)*(-2) =
-12 -1 + 60 + 27 + 8 = 82

5.

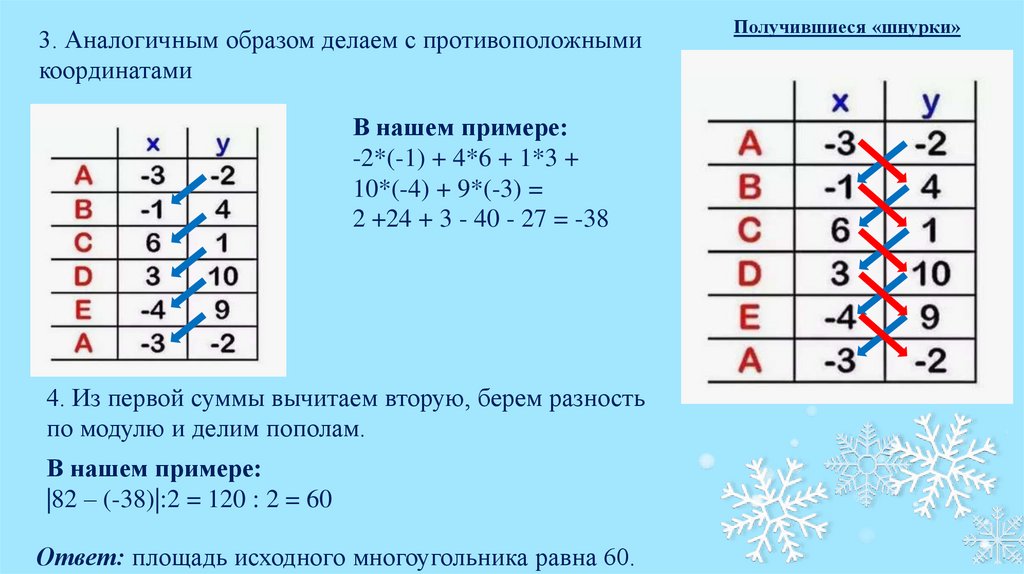
3. Аналогичным образом делаем с противоположными
координатами
В нашем примере:
-2*(-1) + 4*6 + 1*3 +
10*(-4) + 9*(-3) =
2 +24 + 3 - 40 - 27 = -38
4. Из первой суммы вычитаем вторую, берем разность
по модулю и делим пополам.
В нашем примере:
|82 – (-38)|:2 = 120 : 2 = 60
Ответ: площадь исходного многоугольника равна 60.
Получившиеся «шнурки»

6.

Формула Гаусса в олимпиадах

7.

8.

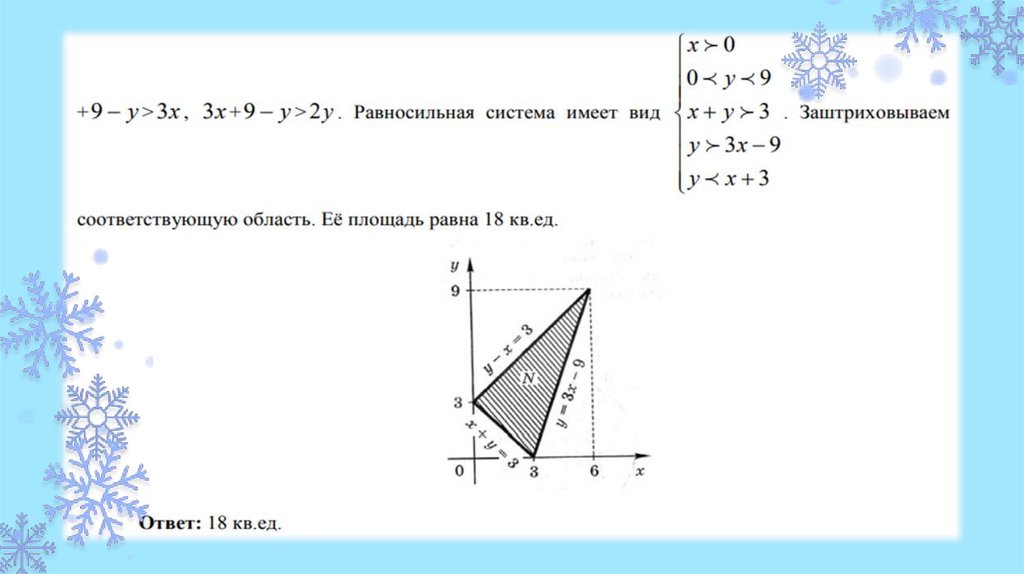
Для начала, используя неравенства,
выразим в каждом y, тем самым найдя
уравнения наших прямых.
Далее найдем точки пересечения этих
прямых или, другими словами, вершины
нашей фигуры M.
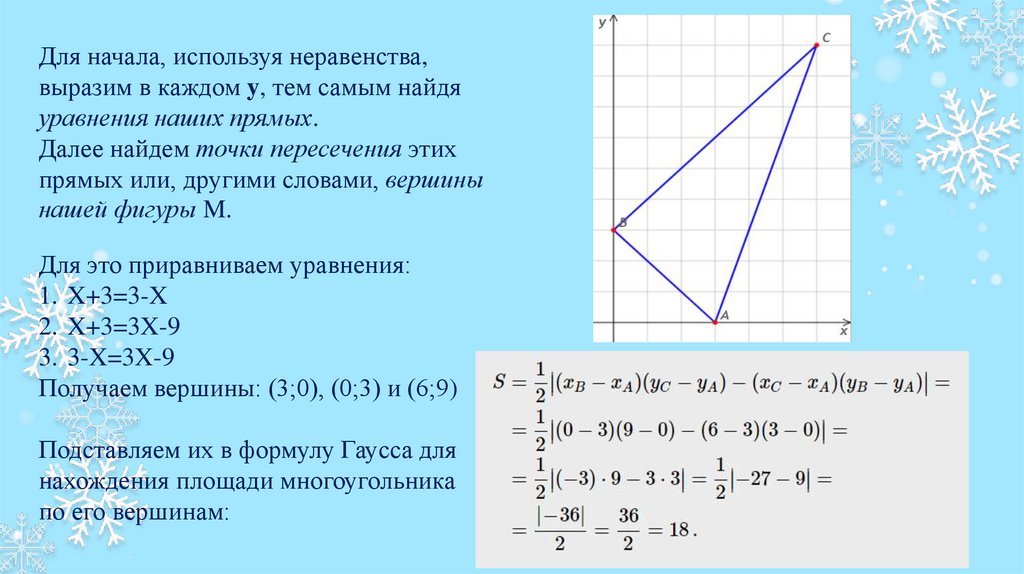
Для это приравниваем уравнения:
1. X+3=3-X
2. X+3=3X-9
3. 3-X=3X-9
Получаем вершины: (3;0), (0;3) и (6;9)
Подставляем их в формулу Гаусса для
нахождения площади многоугольника
по его вершинам:

9.

10.

Применение в реальной жизни:
1. Геодезия и картография.
2. Строительство и архитектура.
3. Градостроительство.
4. Экология.
5. Агроинженерия.
6. Компьютерная графика.

11.

Задание:
1. Постройте фигуру по заданным
координатам.
2. Посчитайте площадь получившейся
фигуры, используя формулу Гаусса.