Подготовка к ГИА-2022

1.

Муниципальное общеобразовательное учреждение
«ЛИЦЕЙ «СПЕКТР» ГОРОДА ТОРЕЗА»
Подготовка к ГИА-2022.
Математика.
Учитель математики
Кирилюк Н.А.

2.

Практикум № 1
"Решение задач
разного уровня сложности"
Задание №7. Производная. Исследование функций.
Первообразная и интеграл.
Задание №12. Наибольшее и наименьшее
значение функции.
Исследование при помощи производной.

3.

Типичные ошибки, допущенные участниками государственной
итоговой аттестации по основным образовательным программам
среднего общего образования в 2021 году
Алгебра и начала анализа.
В ряде работ была отмечена низкая культура ведения математических записей:
•положение дробной черты, запись показателя степени и основания логарифма
относительно строки;
•использование математических символов: знак «объединения множеств» заменяют союзом
«и»;
•вместо знака производной «штрих» пишут запятую или единицу;
•вместо «стационарная точка» пишут «стабильная точка», «стандартная точка» и т.д.;
• термин «область определения функции» путают с терминами «область значений
функции»;
•непонимание отличия точки минимума от минимума функции,
• различия между знаками системы и совокупности.
В тестовой части наибольшее затруднение вызвали задания № 10 и № 12:
№ 10 –
проверка умения применять приобретённые знания в практической
деятельности и повседневной жизни, работа с формулой (не справились 7,2% участников
ГИА);
№ 12 – проверка умения работать с функцией, нахождение точки минимума
(не справились 6,7%)

4.

Типичные ошибки, допущенные участниками государственной
итоговой аттестации по основным образовательным программам
среднего общего образования в 2021 году
Так же в ряде работ (более 5 %) имели место следующие ошибки:
•незнание формул частного и общего случаев простейших тригонометрических уравнений;
(5,1%)
•затруднение в применении метода равносильных переходов при решении логарифмического
неравенства; (5,3%)
•неумение решать квадратные неравенства; (6,2%)
•неумение решать системы неравенств; (5,2%)
•ошибки при выполнении рисунка к системе неравенств; (5,9%)
•ошибки при нахождении производной функции и стационарной (критической) точки; (5,3%)
•неумение определять и записывать промежутки монотонности функции; (5,8 %)
•неумение определять и записывать точки экстремумов и экстремумы функции; (7,1 %)
•ошибки при построении графика (21,9%).
Наибольшее затруднение участников ГИА-2021
вызвало задание № 18, в котором необходимо исследовать функцию и построить ее график.
К его выполнению не приступило менее 3% экзаменуемых. Почти все участники ГИА
справились с исследованием функции. Основное затруднение вызвало построение графика.

5.

Типичные ошибки, допущенные участниками государственной
итоговой аттестации по основным образовательным программам
среднего общего образования в 2021 году
Геометрия.
Низкая графическая культура участников ГИА.
В ряде работ (около 40 %) выявлены ошибки и недочеты в выполнении рисунка:
изображение видимых и невидимых линий;
построение элементов фигуры в соответствии с их свойствами.
Запись единиц измерений:
в условии задания единицы измерения есть, а в ответе – нет; или наоборот;
указаны неверные единицы измерения.
Ошибки в задачах , решение которых опирается на рисунок:
рисунок не выполнен или не соответствует решению.
В тестовой части ошибки встречались в заданиях № 3 и № 8:
№ 3, нахождение площади изображенной фигуры по ее координатам – не справились
8,7% участников ГИА;
№8, нахождение площади боковой поверхности цилиндра по его высоте и радиусу
основания – не справились 6,8% участников ГИА.
В задании № 19 участники ГИА допустили ошибки при:
• изображении призмы (20,9 %);
• обосновании угла наклона диагонали к плоскости основания (22,3%);
• при обосновании равенства боковой стороны и большего основания
равнобокой трапеции, лежащей в основании призмы (11,1 %).

6.

Обобщенный план варианта ЕРЭ 2022 года по МАТЕМАТИКЕ
(профильный уровень) по заданиям.
Задание №1 (Целые числа. Дроби, проценты, рациональные числа. Применение
математических методов для решения содержательных задач из различных областей науки и
практики. Интерпретация результата, учет реальных ограничений).
Задание №2 (Определение и график функции. Элементарное исследование функций.
Основные элементарные функции. Табличное и графическое представление данных).
Задание №3 (Планиметрия. Измерение геометрических величин).
Задание №4 (Классическое определение вероятности. Формула полной вероятности.
Геометрическая интерпретация вероятности. Элементы комбинаторики).
Задание №5 (Уравнения различного вида. Рациональные, иррациональные,
тригонометрические, показательные и логарифмические).
Задание №6 (Треугольник, параллелограмм, ромб, трапеция. Окружность, круг. Свойства
фигур и их комбинаций. Площадь и периметр).
Задание №7 (Производная. Исследование функций. Первообразная и интеграл).
Задание №8 (Прямые и плоскости в пространстве. Многогранники. Тела и поверхности
вращения. Измерения геометрических величин).
Задание №9 (Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования
выражений).
Задание №10 (Задачи с прикладным содержанием. Рациональные, иррациональные,
тригонометрические, показательные и логарифмические уравнения и неравенства).

7.

Обобщенный план варианта ЕРЭ 2022 года по МАТЕМАТИКЕ
(профильный уровень) по заданиям
Задание №11 (Текстовая задача. Движение по прямой, по окружности, по воде. Задачи на
проценты, сплавы, смеси. Задачи на совместную работу и прогрессии).
Задание №12 (Наибольшее и наименьшее значение функции. Исследование при помощи
производной).
Задание №13 (Уравнения. Рациональные, иррациональные, тригонометрические,
показательные и логарифмические. Отбор корней удовлетворяющих заданным условиям).
Задание №14 (Стереометрическая задача. Взаимное расположение прямых и плоскостей в
пространстве. Сечения многогранников. Цилиндр, конус, шар).
Задание №15 (Неравенства. Рациональные, иррациональные, содержащие модуль,
показательные и логарифмические).
Задание №16 (Планиметрическая задача. Многоугольники и их свойства. Окружности и
системы окружностей. Окружности и многоугольники).
Задание №17 (Финансовая математика. Вклады, кредиты, оптимальный выбор).
Задание №18 (Задача с параметром. Расположение корней квадратного трехчлена,
использование симметрий, использование свойств функции).
Задание №19 (Числа и их свойства. Основная теорема арифметики. НОД и НОК.
Последовательности и прогрессии. Сюжетные задачи).

8.

ЕРЭ Математика (профильный уровень)
Задание 7. Производная и первообразная (ОБЗ)
Чтобы решить задание 7 по математике профильного уровня необходимо знать:
1.Задачи подразделяются на несколько видов:
-физический смысл производной.
-геометрический смысл производной и касательная;
-применение производной к исследованию функций;
-первообразная.
2. Знания функции производной и первообразной.
3. Определение понятий и понимание значений производной.
Необходимая теория:
Производная функции
https://ege-study.ru/ru/ege/materialy/matematika/proizvodnaya-funkcii-geometricheskij-smyslproizvodnoj/
Таблица производных
https://ege-study.ru/ru/ege/materialy/matematika/tablica-proizvodnyx/
Первообразная функции
https://ege-study.ru/pervoobraznaya-funkcii-formula-nyutona-lejbnica/
Задание 7 Профильного ЕРЭ по математике — это задачи на геометрический и физический
смысл производной. Это задачи о том, как производная связана с поведением функции. И еще
в этих заданиях встречаются вопросы о первообразной.

9.

Справочник.
Геометрический смысл производной
• Значение производной функции в точке
равно угловому коэффициенту
касательной к графику функции в
этой точке (тангенсу угла между касательной
и осью Ох) f’(хo) = k = tg α
Физический смысл производной
Если точка движется вдоль оси х и ее
координата изменяется по закону x(t), то
мгновенная скорость точки: V(t)=x’(t)
Пусть функция f(х) дифференцируема на интервале
(a;b), хo Є (a; b) и f’(хo) = 0, то:
•при переходе через стационарную точку хo функции
f(х) ее производная меняет знак с «плюса» на «минус»,
то хo – точка максимума функции f(х);
•при переходе через стационарную точку хo функции
f(х) ее производная меняет знак с «минуса» на «плюс»,
то хo – точка минимума функции f(х).
• Производная положительна на промежутках, на
которых функция возрастает и отрицательна на
промежутках, на которых функция убывает.

10.

Справочник.
Первообразная
• Функцию F(x) называют
первообразной для
функции f(х) на заданном
промежутке, если для всех х из
этого промежутка выполняется
равенство F′(x) = f(x).
• Операция нахождения
первообразной функции
называется
интегрированием
Формула для вычисления площади
криволинейной трапеции
(формула Ньютона-Лейбница)
Пусть в прямоугольной системе координат задана
фигура, ограниченная графиком непрерывной
функции у = f (х) , осью Х и прямыми у = a и
у = b. Функция неотрицательна на отрезке [a; b].
Тогда площадь этой фигуры вычисляется по формуле:

11.

Классификация задач
на применение производной
в материалах Открытого банка заданий
по математике при подготовке к профильному ЕРЭ.
Часть 1. Задание №7
1. Геометрический смысл производной.
2. Касательная к графику функции.
3. Физический смысл производной.
4. Применение производной к исследованию
функций.
5. Первообразная и формула Ньютона –Лейбница.

12.

Задание 7. Производная и первообразная (ОБЗ)
1. Геометрический смысл производной
№4
На рисунке изображены
график функции y = f (x) и
касательная к нему в точке с
абсциссой x0. Найдите
значение производной
функции f(x) в точке x0.
Решение 1.
• Начнём с определения знака производной, видим, что в
точке x0 функция убывает, следовательно, её производная
отрицательна. Касательная в точке x0 образует тупой
угол α с положительным направлением оси Х .
• Поэтому из прямоугольного треугольника найдём
тангенс угла φ, смежного с углом α.
Тангенс угла в прямоугольном треугольнике равен
отношению противолежащего катета к прилежащему
у/ = tg φ=
= 0,25
Решение 2.
Выбираем две точки А и В с целыми
координатами на касательной
у/ = ∆у = -2-0 = -2 = - 0,25
∆х 2-(-6)
8
Ответ: - 0,25

13.

Задание 7. Производная и первообразная (ОБЗ)
2. Касательная к графику функции.
№ 3.
Прямая y = 3x + 1 является касательной
к графику функции ax2 + 2x + 3.
Найдите a.
Решение 1
•По смыслу задачи a ≠ 0, а значит, график
заданной функции — парабола.
• Касательная к параболе имеет с ней
единственную общую точку.
• Поэтому необходимо и достаточно,
чтобы уравнение ax2 + 2x + 3 = 3x + 1
имело единственно решение.
• Для этого дискриминант
уравнения ax2 − x + 2 = 0
должен быть равен нулю,
D = 1 − 8а = 0
• откуда а = 0,125.
Решение 2
Прямая y=3x+1 имеет угловой
коэффициент равный 3
Чтобы прямая была касательной к
графику функции y необходимо, чтобы в
точке x функция была равна 3x+1
и угловой коэффициент касательной в
этой точке совпадал с угловым
коэффициентом прямой 3
Подставляем в первое выражение
вместо a x значение 0,5, получаем: х=4
Тогда коэффициент a из второго
уравнения равен 0,125.
Ответ: 0,125.

14.

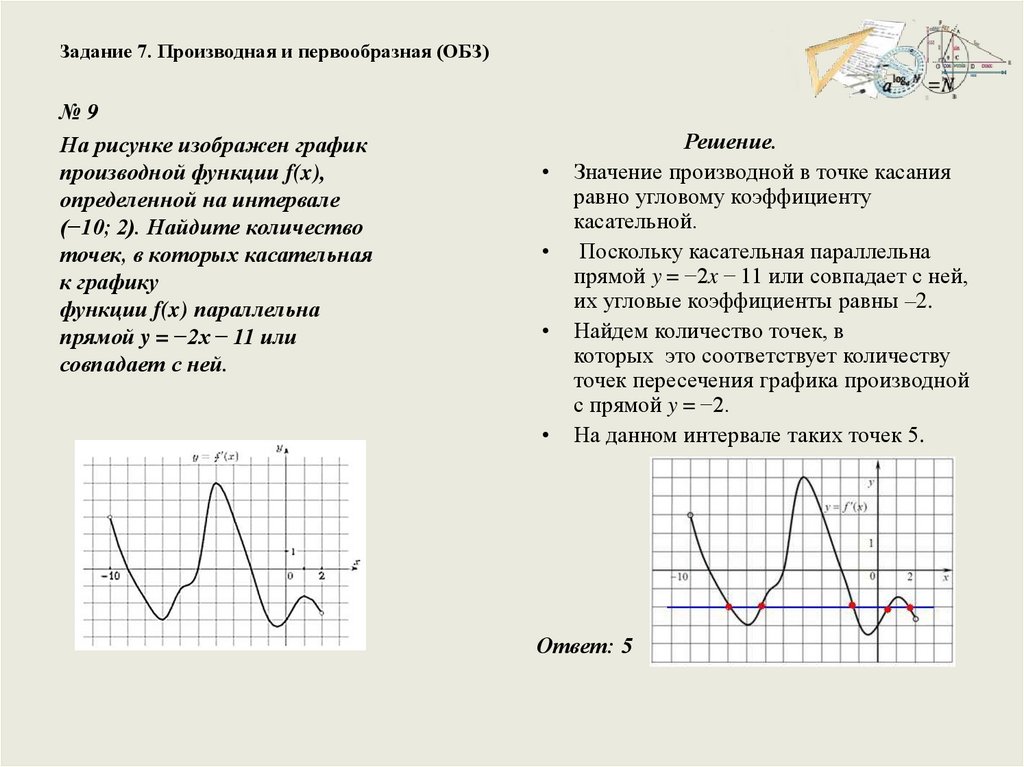
Задание 7. Производная и первообразная (ОБЗ)
№9
На рисунке изображен график
производной функции f(x),
определенной на интервале
(−10; 2). Найдите количество
точек, в которых касательная
к графику
функции f(x) параллельна
прямой y = −2x − 11 или
совпадает с ней.
Решение.
Значение производной в точке касания
равно угловому коэффициенту
касательной.
Поскольку касательная параллельна
прямой y = −2x − 11 или совпадает с ней,
их угловые коэффициенты равны –2.
Найдем количество точек, в
которых это соответствует количеству
точек пересечения графика производной
с прямой y = −2.
На данном интервале таких точек 5.
Ответ: 5

15.

Задание 7. Производная и первообразная (ОБЗ)
3. Физический смысл производной.
№6
Материальная точка движется
прямолинейно по закону
x t 6 t³ 5t 23
(где x –расстояние от точки отсчета в
метрах, t – время в секундах,
измеренное с начала движения).
Найдите ее скорость в (м/с) в момент
времени t 3с.
Решение.
• Скорость движения – это производная от
пути по времени, то есть, чтобы найти
закон изменения скорости нужно
вычислить производную от функции x(t)
по t, получим:
Скорость V(t) = x ́ (t) = -4t³+18t²+5 м/с.
• В момент времени t=3 с скорость
материальной точки равна
V(3)=-4∙3³+18∙3²+5=59 м/с.
Ответ: 59 м/с.
№12.
Материальная точка движется
прямолинейно по закону
x t t² 13t 23
(где x —расстояние от точки отсчета
в метрах, t — время в секундах,
измеренное с начала движения).
В какой момент времени (в секундах)
ее скорость была равна 3 м/с?
Решение.
• Мгновенная скорость движущегося тела
является производной от его координаты
по времени. Это физический смысл
производной.
x(t)=t2−13t+23
x/(t)= 2t - 13
2t - 13 = 3
2t = 16
t=8
Ответ: 8 с.

16.

4. Применение производной к исследованию функций.
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники
делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о
производной. Кто их перепутал, тот задачу не решил.
• Или наоборот. Нарисован график производной — а спрашивают о поведении
функции.
И значит, надо просто внимательно читать условие. И знать, как же связана
производная с поведением функции.
• Если «+», то функция возрастает.
• Если «-» , то функция убывает.
• В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
• В точке минимума производная тоже равна нулю и меняет знак с «минуса» на
«плюс».

17.

Задание 7. Производная и первообразная (ОБЗ)
4. Применение производной к исследованию функций.
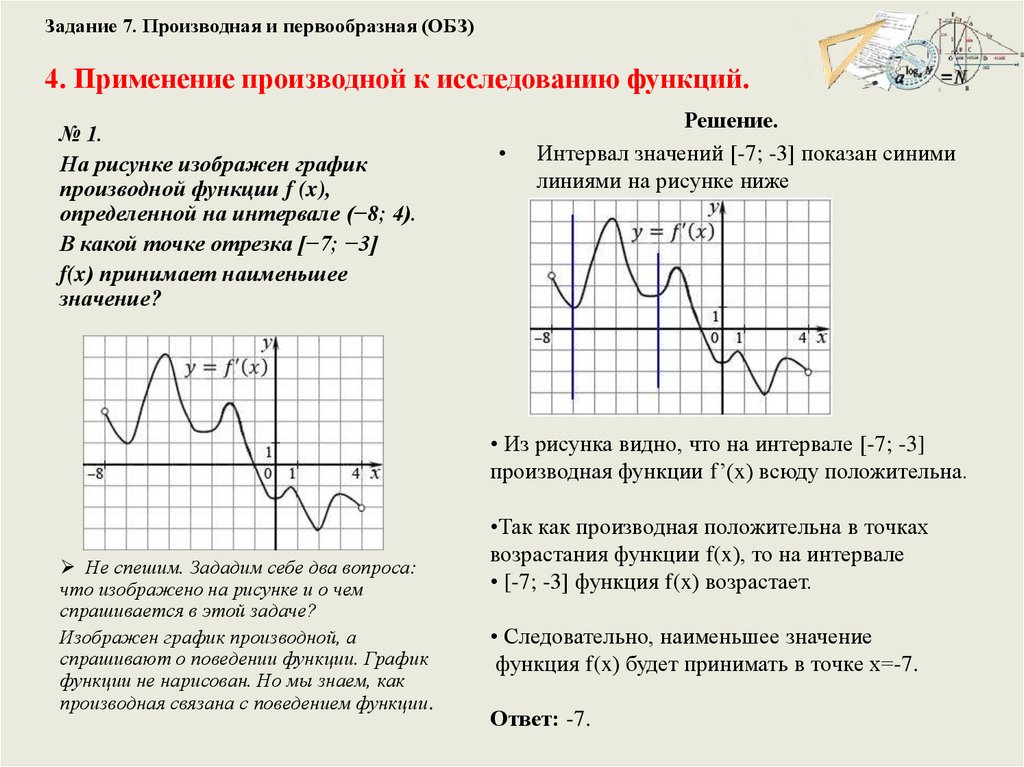
№ 1.
На рисунке изображен график
производной функции f (x),
определенной на интервале (−8; 4).
В какой точке отрезка [−7; −3]
f(x) принимает наименьшее
значение?
Решение.
Интервал значений [-7; -3] показан синими
линиями на рисунке ниже
• Из рисунка видно, что на интервале [-7; -3]
производная функции f’(x) всюду положительна.
Не спешим. Зададим себе два вопроса:
что изображено на рисунке и о чем
спрашивается в этой задаче?
Изображен график производной, а
спрашивают о поведении функции. График
функции не нарисован. Но мы знаем, как
производная связана с поведением функции.
•Так как производная положительна в точках
возрастания функции f(x), то на интервале
• [-7; -3] функция f(x) возрастает.
• Следовательно, наименьшее значение
функция f(x) будет принимать в точке x=-7.
Ответ: -7.

18.

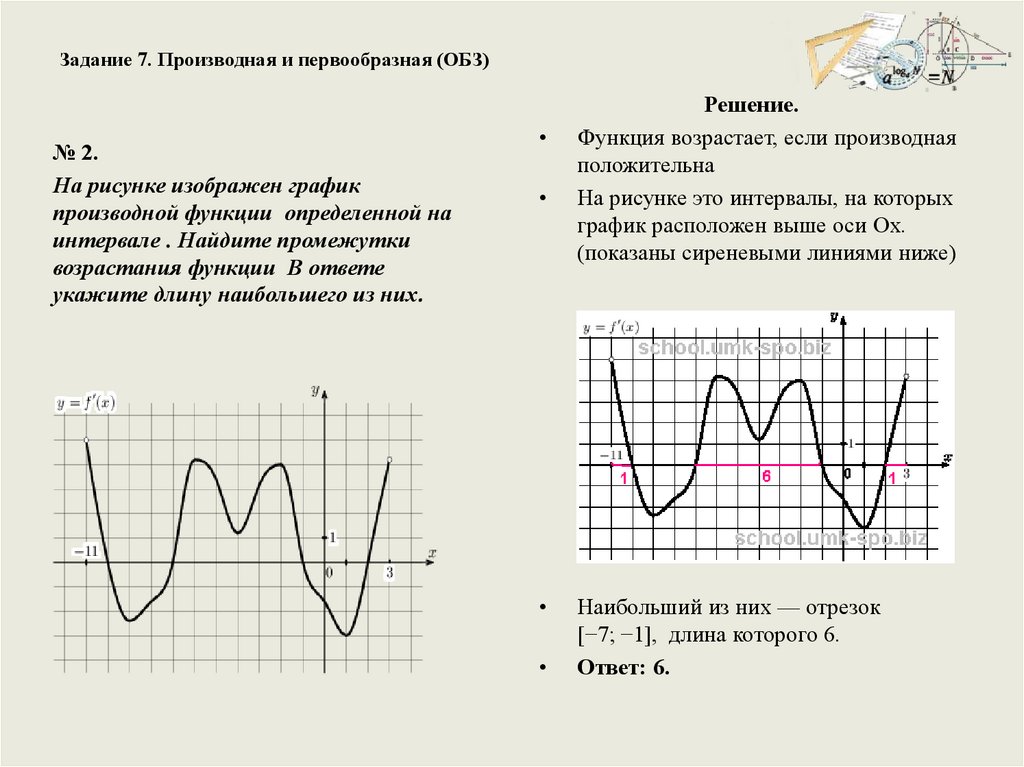
Задание 7. Производная и первообразная (ОБЗ)
№ 2.
На рисунке изображен график
производной функции определенной на
интервале . Найдите промежутки
возрастания функции В ответе
укажите длину наибольшего из них.
Решение.
Функция возрастает, если производная
положительна
На рисунке это интервалы, на которых
график расположен выше оси Ох.
(показаны сиреневыми линиями ниже)
Наибольший из них — отрезок
[−7; −1], длина которого 6.
Ответ: 6.

19.

Задание 7. Производная и первообразная (ОБЗ)
№ 14.
На рисунке изображен график
производной функции f(x),
определенной на интервале (−18; 6).
Найдите количество точек минимума
функции f(x) на отрезке [−13;1].
Очень внимательно читаем условие задачи.
Изображен график производной, а
спрашивают о точках минимума функции.
Решение.
Так как задан график производной, то на
заданном интервале нужно найти точки
пересечения с осью OX. Если график
расположен ниже оси ОХ, то знак
производной "-". Если график выше оси ОХ,
то знак производной «+».
Точки минимума соответствуют точкам
смены знака производной с минуса на
плюс. На отрезке [−13;1] функция имеет
одну точку минимума x = −9
Ответ:1

20.

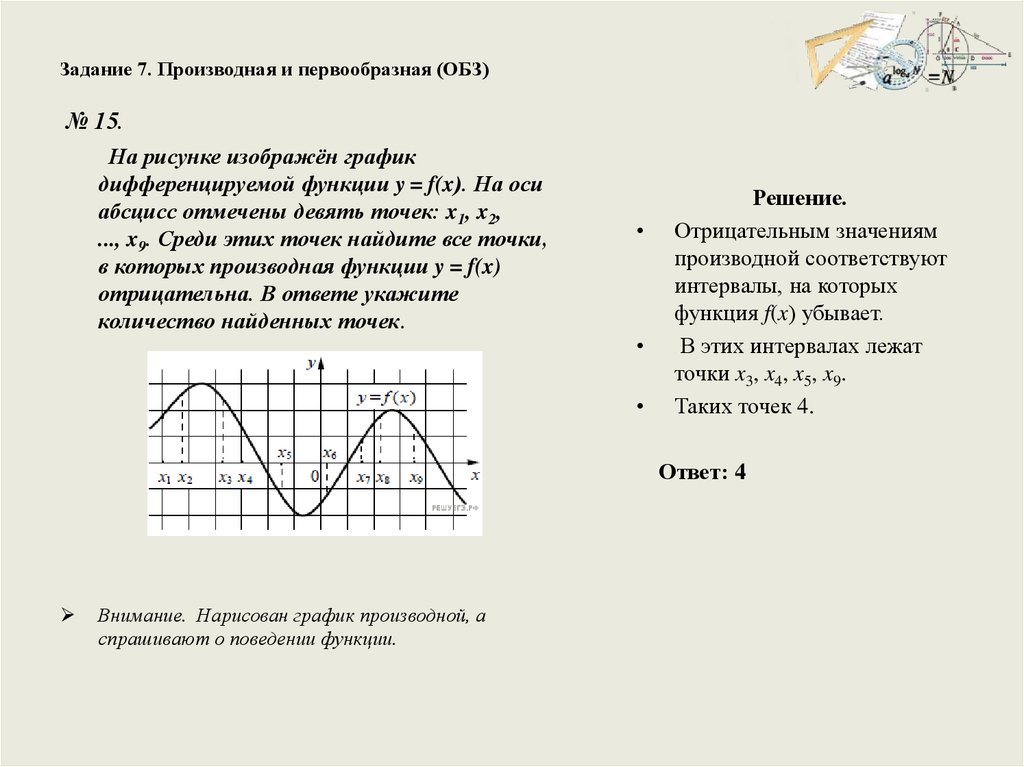
Задание 7. Производная и первообразная (ОБЗ)
№ 15.
На рисунке изображён график
дифференцируемой функции y = f(x). На оси
абсцисс отмечены девять точек: x1, x2,
..., x9. Среди этих точек найдите все точки,
в которых производная функции y = f(x)
отрицательна. В ответе укажите
количество найденных точек.
Решение.
Отрицательным значениям
производной соответствуют
интервалы, на которых
функция f(x) убывает.
В этих интервалах лежат
точки x3, x4, x5, x9.
Таких точек 4.
Ответ: 4
Внимание. Нарисован график производной, а
спрашивают о поведении функции.

21.

Классификация задач
на применение производной
в материалах Открытого банка заданий
по математике при подготовке к профильному ЕРЭ.
Часть 2. Задание №12
Задание 12 второй части Профильного ЕРЭ по математике —
это нахождение точек максимума и минимума функции,
также наибольших и наименьших значений функции с
помощью производной.
Типы задач
1. Нахождение точек максимума и минимума функций
2. Исследование сложных функций
3. Нахождение наибольших и наименьших значений
функций на отрезке

22.

Задание 12. Наибольшее и наименьшее значение функций. (ОБЗ)
1. Нахождение точек максимума и минимума функций
№5.
Найдите точку
минимума функции
y = (x+16)e16−x
Решение
Будем искать точку максимума функции с помощью
производной. Найдем производную и приравняем ее к нулю.
Найдем производную
у/ = e16−x - (x+16)e16−x
у/ =e16−x( 1 - х - 16) =e16−x(-х-15)
у/ = 0
e16−x(-х-15) = 0
e16−x ≠ 0 e16−x > 0
-х-15 = 0
х = - 15
Знак производной на интервалах:
+
_
_________o__________ у/
-15
x = -15 точка максимума
(производная меняет знак с + на -)
Ответ: -15

23.

Задание 12. Наибольшее и наименьшее значение функций. (ОБЗ)
2. Исследование сложных функций
№ 1.
Найдите точку максимума функции
Решение.
В скобках - квадратичная функция, графиком которой является
парабола. Ветви параболы направлены вниз (a=-1), значит точка
максимума будет в вершине параболы
х = -b/2a, в нашем случае — в точке −7.
Основание логарифма 8 > 1 ⇒ логарифмическая функция возрастающая.
Поскольку функция
возрастает, и функция
определена в точке −7, она также достигает в ней максимума.
Ответ: -7

24.

Задание 12. Наибольшее и наименьшее значение функций. (ОБЗ)
2. Исследование сложных функций
№8
Найдите наименьшее значение функции
Решение 1.
Функция будет принимать наименьшее
значение при тех значениях х, при
которых подкоренное выражение
принимает наименьшее значение.
• Подкоренное выражение – квадратный
трехчлен.
Выделяем полный квадрат
x2–6x+13=(x2–6x+9)+4=(x–3)2+4 ≥ 0 при
всех х
• Поэтому наименьшее значение
функции достигается в точке 3,
• и равно 2
Решение 2.
• Рассмотрим функцию y = x2 - 6x + 13,
графиком является парабола, ветви
направлены вверх. Вторая координата её
вершины и является наименьшим
значением (у=2)
• Поскольку
функция
возрастающая, а
подкоренное выражение положительно
при всех значениях переменной, заданная
функция достигает наименьшего
значения в той же точке, в которой
достигает наименьшего значения
подкоренное выражение Квадратный
трехчлен с положительным старшим
коэффициентом х=1 достигает
наименьшего значения в точке
х = -b/2a , х=3,
Следовательно, наименьшее значение
заданной функции у=2
Ответ:2

25.

Задание 12. Наибольшее и наименьшее значение функций. (ОБЗ)
3. Нахождение наибольших и наименьших значений
функций на отрезке
№ 10
Найдите наименьшее значение
функции
на отрезке
Решение
1. Найдем производную заданной функции:
у/ = 3 x2 +18 х=3х(х+6)
2. Стационарные точки: 3х(х+6)=0
Производная обращается в нуль в точках 0 и -6,
заданному отрезку принадлежит число 0.
3. Вычислим значение функции в точке 0 и на
концах отрезка
Мы помним, что наибольшее
значение функции на отрезке
может достигаться либо в точке
максимума, либо на конце отрезка.
Эти случаи показаны на рисунке.
у(0)=15
у(-1,5)=31
у(1,5)=38
Наименьшим значением на заданном отрезке
является число 15
Ответ :15

26.

РЕСУРСЫ ПО ПОДГОТОВКЕ ЕРЭ
Открытый банк заданий. Математика (2022)
https://gia.resobrnadzor.ru/государственная-итоговаяаттестация/открытый-банк-заданий/
Отдел математики Донецкого РИДПО, «Готовимся к ГИА»,
http://ippo-vm.at.ua/index/0-31
• Подготовка к ЕГЭ по математике базового и профильного уровня
https://ege-study.ru/ru/ege/materialy/matematika/
• СПРАВОЧНИК ДЛЯ ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ
https://ege-study.ru/spravochnik-anny-malkovoj/