Similar presentations:
Методические рекомендации для учителя математики «Организация работы по восполнению пробелов в званиях учащихся»
1.
2021Методические рекомендации
для учителя математики
«Организация работы по
восполнению пробелов в
званиях учащихся»
Творческая группа
учителей математики РК
2.
Творческий коллектив учителей математикиРуководитель - Середкин В.П. учитель математики, педагог-мастер, Павлодарская область,
Павлодарский район, КГУ Чернорецкая СОШ № 1
Фазылова Т. М. Государственное коммунальное учреждение "Средняя школа №1 имени
Жамбыла" государственного учреждения "Отдел образования по Балхашскому району
Управления образования Алматинской области", Высшая категория
Середенко Э. В., Костанайская область, КГУ «Общеобразовательная школа №1 города Тобыл
отдела образования Костанайского района» Управления образования акимата Костанайской
области, педагог-исследователь
Рубцова В. В., Костанайская область, КГУ «Новопокровская общеобразовательная школа
отдела образования Узункольского района» Управления образования акимата Костанайской
области педагог-эксперт
Арютина С. И., Педагог-эксперт, Северо-Казахстанская область, КГУ «Заградовская средняя
школа» КГУ «Отдел образования Есильского района» КГУ «Управление образования акимата
Северо-Казахстанской области»
Белгибаева Н.Б. - учитель математики, высшая категория, г. Кызылорда , СШ№ 6 им.
М.А.Сужикова
Кусаинова А.М. - учитель математики, вторая категория, г. Павлодар,
КГУ СОШ №15
Гапонова И. Б., педагог-исследователь, Северо-Казахстанская область, КГУ «Булаевская
средняя школа№2» КГУ «Отдел образования района М.Жумабаева» КГУ «Управление
образования акимата Северо-Казахстанской области»
Бредихина Н. В. учитель математики и информатики, педагог- эксперт КГУ «Афанасьевская
средняя школа» КГУ «Отдел образования района Шал акына» КГУ «Управления образования
Северо-Казахстанской области»
Подгорнова О.В. учитель математики, педагог-исследователь, ВКО, Шемонаихинский район,
КГУ «Убинская общеобразовательная средняя школа» отдела образования по
Шемонаихинскому району управления образования ВКО
Романович Ю. И., Костанайская область, Коммунальное государственное учреждение
"Гимназия отдела образования Житикаринского района" Управления образования акимата
Костанайской области, педагог-исследователь
Маркель Т. П., Северо-Казахстанская область, район М.Жумабаева, КГУ «Таманский
комплекс школа-ясли-сад», педагог-эксперт
Жуменко С. Н., Алматинская обл., г.Талдыкорган, КГУСШГ 16, учитель высшей категории
Сабитова С. А., учитель математики 1 категории КГУ «Средняя школа №18» отдела
образования по городу Усть-Каменогорску управления образования Восточно-Казахстанской
области
Ткаченко Е.Ю. Костанайская область, г.Руднвй, КГУ "Общеобразовательная школа № 1
отдела образования города Рудного" Управления образования акимата Костанайской области,
педагог-эксперт
Черненко
Н.
Д.,
педагог-исследователь,
Северо-Казахстанская
область,
КГУ
«Воскресеновская средняя школа» КГУ «Отдел образования Мамлютского района» КГУ
«Управление образования акимата Северо-Казахстанской области»
Куатбекова
А.
С.,
Карагандинская
область
Бухар-Жырауский
район
КГУ
«Общеобразовательная школа имени Талгата Бигелдинова» отдела образования БухарЖырауского района управления образования Карагандинской области, педагог-эксперт
3.
Стурова О. А., Жамбылская область Таласский район г. Каратау КГУ «ШКОЛА ЛИЦЕЙ №1отдела образования Таласского района управления образования акимата Жамбылской
области», категория высшая
Кузьмина И. В., учитель физики и математики, Костанайская область, КГУ «Новоселовская
основная средняя школа отдела образования Карасуского района» Управления образования
акимата Костанайской области. Категория : педагог – исследователь.
Романенко Н. И., учитель математики,
КГУ «Петропавловская средняя школа»
государственного учреждения «Отдел образования Каргалинского района Управления
образования Актюбинской области». Категория : высшая.
Жунусова Г. С. Педагог-модератор Павлодарская область Щербактинский район
Чигириновская СОШ
Рецензент – Сипатова А.Ш., методист ИЦРО
4.
Каждый учитель во время учебного года проводит работу поликвидации пробелов знаний учащихся – это системная работа, направленная
на повышение качества знаний и развитее основных компетенций у
учащихся по предмету. Последние полтора года обучения в условиях
ограничительных мер снизили уровень знаний учащихся. Поэтому для того
чтобы на должном уровне развить основные компетенции учащихся по
предмету учителю необходимо приложить ряд усилий.
В настоящее время в современной школе в условиях обновленного
содержания образования для оценивания знаний учащихся используется
формативное и суммативное оценивание. Но зачастую все забывают еще об
одном виде оценивания это диагностическое.
Диагностическое
Формативное
Суммативное
Определение исходного Это оценивание в Итоговое
Что
уровня
процессе обучения, оценивание,
такое?
сформированности
наблюдения,
когда учитель
компетентностей
анализа учебных ставит отметку
учащегося
достижений
учащимся
учащихся,
при
котором
выполняется
корректировка
Проводится в начале Проводится
Проводится в
Когда
применяе этапа обучения (темы, регулярно во время конце изучения
раздела,
четверти, урока
темы, раздела,
тся?
учебного года) или в
четверти,
начале работы с новым
учебного года
классом или учеником
Позволяет
определить Позволяет
Позволяет
Почему
предоставить
применяе уровень учащихся и отслеживать
внести коррективы в прогресс учащихся информацию о
тся?
планы
учителя и
вносить том, что узнали
(календарные,
изменения
в учащиеся
в
поурочные)
процесс обучения процессе
(корректируются
обучения.
планы уроков)
Диагностическое тестирование является неотъемлемой частью
процесса оценивания, так как оно позволяет определить уровень
сформированности компетенций учащихся. И дает возможность выстроить
свою работу по повышению уровня знаний учащегося на конкретном этапе
обучения.
Диагностическое оценивание лучше всего проводить в начале учебного
года или на первом занятии изучения темы, учебного раздела, главы. Оно
5.
позволяет учителю корректировать учебный план с учетом потребностейучащихся, прогнозировать и преодолевать потенциальные трудности в
обучении и учении.
Данный вид оценивания помогает педагогу определить пробелы в
знаниях по учебной программе. По итогам диагностического оценивания у
учителя появляется возможность выявить цели обучения, по которым у
учащихся имеются пробелы в знаниях, а также определить цели обучения,
какие соответствуют и какие не соответствуют целям обучения по предмету в
текущем учебном году. На основе этих данных учителю рекомендуется
разработать план индивидуальной работы по восполнению пробелов в
званиях учащихся. Если цели обучения, по которым учащиеся показали
пробелы знаний, соответствуют целям обучения в новом учебном году, то
рекомендуется включать их в содержание краткосрочных планов и
рассматривать их на уроке. Краткосрочный план урока организуется с учетом
интегрированных целей двух последовательных классов. Например:
Напомним, что формативное оценивание применяется для определения
прогресса учащихся с учетом индивидуальных особенностей усвоения
материала (темп выполнения работы, способы освоения темы и т. п.), а также
в целях выработки рекомендаций для достижения успеха. Учитель
использует формативное оценивание для своевременной корректировки
обучения, внесения изменений в планирование, а учащийся – для улучшения
качества выполняемой им работы. Прогресс учащегося определяется как
достижение определенных результатов, заложенных в целях обучения в
рамках образовательных областей, на основании конкретной работы,
выполненной учащимся.
Формативное и суммативное оценивание являются двумя из наиболее
широко используемых видов оценивания в образовании. Они дополняют
6.
друг друга: формативное оценивание проверяет успеваемость в процессеобучения, а суммативное оценивание служит «итоговой оценкой».
Качество формативного оценивания на уроке будет влиять на
результаты суммативного оценивания. Но без результатов диагностической
оценки учитель не сможет применить формативное оценивание на должном
уровне. Сохраняя такую последовательность при оценивании можно
добиться высокого уровня обучения.
Диагностическое
Формативное
Суммативное
После проведения диагностического оценивания учителю необходимо
провести анализ результатов данной работы учащихся.
Мы предлагаем проводить анализ по следующей схеме:
Анализ диагностического оценивания учащихся _____ класса
по _______________ в 20 __ - 20 __ учебном году
входной, промежуточный (подчеркнуть нужное)
№ пп
ФИ
Цели обучения
учащегося Проверяемая Цели
…….
цель
1
2
3
……
В данной таблице в целях обучения необходимо указать все цели,
которые проверяются в контрольной работе. Проведение анализа
диагностического оценивания в таком виде позволяет учителю определит,
кто из учеников достиг данных целей, кто не достиг, и на основе этого
выстроить коррекционную работу как групповую, так и индивидуальную.
Творческой группой были разработаны примерные комплексные
диагностические работы на начало года. Контрольные работы составлены на
основе формата итоговой аттестации.
7.
Комплексная диагностическая работапо математике 5 класс 2021-2022 учебный год
авторы: Середенко Эльвира Владимировна, Костанайская область, КГУ
«Общеобразовательная школа №1 города Тобыл отдела образования Костанайского
района» Управления образования акимата Костанайской области, педагогисследователь
Рубцова Виктория Викторовна, Костанайская область, КГУ «Новопокровская
общеобразовательная школа отдела образования Узункольского района» Управления
образования акимата Костанайской области педагог-эксперт
Продолжительность – 45 минут
Типы заданий: МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Многозначные числа.
1.1
МВО
4.1.1.3 Определять разрядный и классовый
Последовательности
состав многозначных чисел и общее
чисел
количество разрядных единиц,
раскладывать на сумму разрядных
слагаемых
Письменное сложение
1.2
МВО
4.1.2.8 - применять алгоритм сложения и
и вычитание
вычитания многозначных чисел
многозначных чисел
Задачи на движение.
1.3
МВО
4.5.1.2 ** - использовать при решении задач
зависимость между величинами: скорость,
время, расстояние
Умножение и деление
1.4
МВО
4.1.2.11** - применять алгоритм умножения
на трехзначное число
и деления на трехзначное число
Алгоритм умножения
1.5
МВО
4.1.2.13** - применять алгоритм деления
и деления на
многозначных чисел на двух/трехзначное
трехзначное число
число, когда в записи частного есть ноли и
алгоритм обратного действия умножения
Проценты
1.6
МВО
4.1.1.5 понимать, что процент – сотая часть
целого
Сложение и
1.7
МВО
4.2.1.4 выполнять сложение и вычитание
вычитание дробей
обыкновенных дробей с одинаковыми
знаменателями;
Правильные и
1.8
МВО
4.1.1.6
различать
правильные,
неправильные дроби
неправильные дроби, смешанные числа;
Уравнения
2.1
РО
4.2.2.2 решать уравнения вида
39+490:k=46, 230·а+40=1000:2
Числовые и
2.2
РО
4.2.1.7 определять порядок действий
буквенные
и находить значения выражений со
выражения.
скобками и без скобок, содержащих более
Преобразование
четырех арифметических действий
выражений
Составление
2.3
РО
4.2.1.3 составлять выражения с переменной
выражений с
и использовать их для решения задач
переменными по
задачам
8.
1 вариантЗадания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Выберите число, которое верно записано в виде суммы разрядных слагаемых
A) 712 305 = 700 000 + 10 000 + 2 000 + 30 + 5
B) 452 132 = 400 000 + 50 000 + 2 000 + 100 + 30 + 2 +
C) 48 574 = 48 000 + 500 + 74
D) 157 659 = 100 000 + 5 000 +7 000 + 600 + 50 + 9
E) 2 138 957 = 200 000 + 138 000 + 900 + 50 + 7
1.2. Вычислите 528 076 – 64 938, 445 200 + 4 128. Выберите верный ответ.
A) 453 138, 459 328
B) 440 139, 495 238
C) 463 138, 449 328 +
D) 455 130, 450 300
E) 447 000, 449 000
1.3. Выберите формулу вычисления расстояния S:
A)
+
B)
C)
D)
E)
1.4. Вычислите:
A) 6
B) 7
C) 8
D) 9 +
E) 10
1.5. Вычислите:
A) 19 090
B) 18 050
C) 20 090
D) 19 070
E) 18 070 +
1.6. Определите верную запись дроби
A) 63% +
B) 65%
C) 60%
D) 67%
E) 37%
1.7. Вычислите:
A)
в виде процента, используя знак %.
9.
B)+
C)
D)
E)
1.8. Выберите неправильную дробь.
A)
B)
C)
D) +
E)
Задания уровня В
2.1. Решите уравнение
2.2.
Определите
[4]
порядок
действий
и
вычислите
значение
[4]
выражения
2.3 Запишите буквенное выражение по задаче.
Собрали 320 кг помидоров. В m ящиков разложили по 25 кг. Сколько килограммов
помидоров осталось?
[3]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Выберите число, которое верно записано в виде суммы разрядных слагаемых
A) 315 145 = 300 000 + 10 000 + 5 000 + 100 + 40 + 5 +
B) 458 361 = 400 000 + 50 000 + 8 000 + 30 + 2
C) 79 479 = 79 000 + 400 + 79
D) 436 655 = 100 000 + 3 000 +6 000 + 600 + 50 + 5
E) 5 472 952 = 500 000 + 472 000 + 900 + 50 + 2
1.2. Вычислите 785 025 – 59 120, 654 500 + 8 367. Выберите верный ответ.
A) 753 138, 659 328
B) 740 139, 695 238
C) 763 138, 649 328
D) 755 130, 650 300
E) 725 905, 662 867 +
1.3. Выберите формулу вычисления расстояния V:
A)
B)
C)
D)
E)
+
10.
1.4. Вычислите:A) 6 +
B) 7
C) 8
D) 9
E) 10
1.5. Вычислите:
A) 16 060
B) 19 050
C) 17 070 +
D) 19 070
E) 18 070
1.6. Определите верную запись дроби
в виде процента, используя знак %.
A) 63%
B) 65%
C) 60%
D) 67%
E) 37% +
1.7. Вычислите:
A)
B)
+
C)
D)
E)
1.8. Выберите неправильную дробь.
A)
B)
+
C)
D)
E)
Задания уровня В
2.1. Решите уравнение
2.2.
Определите
[4]
порядок
действий
и
вычислите
значение
[4]
выражения
2.3 Запишите буквенное выражение по задаче.
Собрали 640 кг помидоров. В m ящиков разложили по 40 кг. Сколько килограммов
помидоров осталось?
[3]
11.
Критерий оцениванияВыбирает число, верно
записанное в виде суммы
разрядных слагаемых
Выполняет сложение и
вычитание многозначных чисел
Выбирает формулу вычисления
расстояния
Выполнять деление с
многозначного числа на
трехзначное число
Выполнять деление
многозначного числа на
двузначное
Выбирает верную запись дроби в
виде процента
Выполняет сложение и
вычитание обыкновенных дробей
с одинаковыми знаменателями
Выбирает неправильную дробь
Выполняет решение уравнения
Вычисляет значение выражения
№
задания
1.1
Дескриптор
Балл
Умеет определять разрядный и
классовый состав и раскладывать на
сумму разрядных слагаемых
Применяет свойства сложения и
вычитания многозначных чисел
Знает формулы нахождения
скорости и расстояния
Применяет алгоритм деления
многозначных чисел
1
1.5
Применяет алгоритм деления
многозначного числа на двузначное
1
1.6
Умеет представлять обыкновенную
дробь в виде процента
Использует алгоритм сложения и
вычитания обыкновенных дробей с
одинаковыми знаменателями
Различает правильные,
неправильные и смешанные числа
Выполняет действие деления в
правой части уравнения
Находит неизвестное слагаемое
Находит неизвестный множитель
Записывает корень уравнения
Выполняет вычитание в скобках
Выполняет умножение
трехзначного числа на двузначное
Складывает многозначные числа
Записывает получившийся ответ
Умеет составлять буквенное
выражение по условию задач
Находит неизвестный множитель
Записывает ответ задачи
1
1.2
1.3
1.4
1.7
1.8
2.1
2.2
Составляет буквенное выражение 2.3
по условию задачи
Итого
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
19
Комплексная диагностическая работа
по математике 5 класс 2021-2022 учебный год
автор: Арютина Светлана Иосифовна, Педагог-эксперт, Северо-Казахстанская
область, КГУ «Заградовская средняя школа» КГУ «Отдел образования Есильского
района» КГУ «Управление образования акимата Северо-Казахстанской области»
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задания задания
Числовые и буквенные
А1
МВО
4.2.1.7 определять порядок действий и
12.
выражения.Преобразование
выражений.
Письменное сложение
и вычитание
многозначных чисел
Письменное деление на
двухзначное число с
нулем в частном
А2
МВО
А3
МВО
Письменное сложение
и вычитание
многозначных чисел
А4
МВО
Алгоритм умножения и
деления на трехзначное
число
Составление
выражений с
переменными по
задачам
Уравнения
А5
МВО
А6
МВО
В1
РО
Числовые и буквенные
выражения при
решении задач
В2
РО
находить значения выражений со
скобками и без скобок, содержащих более
четырех арифметических действий;
4.1.2.8 применять алгоритмы сложения и
вычитания многозначных чисел;
4.1.2.13 применять алгоритмы деления
многозначных чисел на двух/трехзначное
число, когда в записи частного есть нули
и алгоритмы обратного действия
умножения;
4.1.2.3 применять свойства сложения
и
умножения при выполнении вычислений
с многозначными числами;
4.1.2.11** применять алгоритмы
умножения и деления на трехзначное
число;
4.2.1.3 составлять выражения с
переменной и использовать их для
решения задач;
4.2.2.2 решать уравнения вида
39+490 : k = 46; 230 · а + 40 = 1000 : 2.
4.5.1.7 моделировать и решать задачи в 34 действия разными способами и
определять наиболее рациональный;
1 вариант
Уровень А
А1. Какое действие выполняется последним:
( 912:114+6 440:23) : 16 - 256020
1) вычитание;
2) деление;
3) умножение;
4) сложение?
А2. На сколько разность чисел 4 236 и 1 487 меньше их суммы?
1) 2749;
2) 2 974;
3) 4 236;
4) 1 487;
5) 5 723;
6) 8 474.
А3. Найди значение выражения: 820 680 : 21. Выбери правильный ответ.
1) 398;
2) 3908;
3) 39080;
4) 3980;
5) 39008;
6) 39800
А4. Не вычисляя, укажите правую часть равенства: (15562 + 143) *231
1) 15562*231+143 ;
2) 15562 + 143*231;
3) 15562 *231 +
143*231;
4) 15562+143;
5) 15562 +(143*231);
6) (15562*231) +143 ?
А5. Выполни умножение: 1235 * 201
1) 248235;
2) 1235;
3) 25935;
4) 25935;
5) 3705;
6)
2471235
А6. Найдите верное буквенное выражение для задачи:
Фермеры собрали 260 кг помидоров. В m ящиках сложили по 24 кг. Сколько килограммов
помидоров осталось?
1) 260*m+ 24;
2) 260+ 24*m;
3) 260*m-24 ;
4) (260-24)*m;
5) (260+24)*m;
6) 260-24*m
В1. Решить уравнение:
Уровень В
110*а + 20 = 1140:2
[2 балла]
13.
В2. С фермы на молочный завод отправили 208 л молока в машине цистерне и ещё 15бидонов по 30 л в каждом. После этого на ферме осталось 400 л молока. Сколько литров
молока надоили на ферме за день?
[2 балла]
2 вариант
Уровень А
А1. Какое действие выполняется последним:
( 131 364:41-19 000:25 ) : 52 + 20
1) вычитание;
2) деление;
3) умножение;
4) сложение?
А2. На сколько разность чисел 5125 и 2376 меньше их суммы?
1)7501;
2) 4752;
3) 2749;
4) 10250;
5) 5125;
6) 2376.
А3. Найди значение выражения: 740 160 : 36. Выбери правильный ответ.
1) 256;
2) 2560;
3) 20560;
4) 2506;
5) 25006;
6)
25600
А4. Не вычисляя, укажите правую часть равенства: (562 + 12743) *102
2) 562*102+12743 ;
2) 562 + 12743*102;
3) 562 *102 +
12743*102;
4) 562+12743;
5) 562 +(12743*102);
6) (562*102)
+12743 ?
А5. Выполни умножение: 2217 * 205
1)454485;
2) 11085;
3) 55425;
4) 454 485;
5) 55325;
6)
45525
А6. Найдите верное буквенное выражение для задачи:
Фермеры собрали 510 кг помидоров. В m ящиках сложили по 25 кг. Сколько килограммов
помидоров осталось?
1) 510*m+ 25;
2) 510+ 25*m;
3) 510*m - 25;
4) (510-25)*m;
5) (510+25)*m;
6) 510-25*m
Уровень В
В1. Решить уравнение: 93*а - 86 = 200 : 2
[2 балла]
В2. С фермы на молочный завод отправили 152 л молока в машине цистерне и ещё 12
бидонов по 30 л в каждом. После этого на ферме осталось 600 л молока. Сколько литров
молока надоили на ферме за день?
[2 балла]
Критерий оценивания
№
Дескриптор
Балл
задания
Определяет порядок действий в
А1
Умеет определять порядок
1
выражениях со скобками
действий в выражениях со
скобками
Выполняет сложение и вычитание
А2
Применяет алгоритмы сложения и 1
многозначных чисел
вычитания многозначных чисел
Выполняет деление многозначных А3
Применяет алгоритмы деления
1
чисел на двузначное число, когда в
многозначных чисел на
записи частного есть нули
двузначное число, когда в записи
частного есть нули
Выполняет сложение и умножение А4
Применяет свойства сложения и
1
при выполнении вычислений с
умножения при выполнении
многозначными числами
вычислений с многозначными
числами
Находит значение выражения,
А5
Применяет алгоритм умножения
1
используя алгоритм умножения на
на трехзначное число
трехзначное число
Верно определяет выражение с
А6
Умеет составлять буквенное
1
переменной при использовании их
выражение по условию задач
14.
для решения задачВ1
Выполняет решение уравнения
Выполняет действие деление в
правой части; и находит
неизвестное слагаемое
Находит неизвестный множитель
и записывает ответ
Определяет способ решения
задачи
Находит общее количество
молока
1
1
В2
1
Верно составляет модель задачи и
решает задачи разными способами,
при этом определяет наиболее
1
рациональный
Итого:
10
Комплексная диагностическая работа
по математике за 6 класс 2021-2022 учебный год
авторы: Белгибаева Н.Б. - учитель математики, высшая категория, г. Кызылорда , СШ№ 6
им. М.А.Сужикова
Кусаинова А.М. - учитель математики, вторая категория, г. Павлодар,
КГУ СОШ №15
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Степень
1.1
МВО
5.1.2.4 записывать произведение одинаковых
чисел в виде степени
Уравнение
1.2
МВО
5.2.2.1 решать уравнения на основе правил
нахождения неизвестных компонентов
арифметических действий
Множество
1.3
МВО
5.4.1.1 усвоить понятия множества и его
элементов, пустого множества
Признаки делимости на
1.4
МВО
5.1.2.5 применять признаки делимости
3;6
натуральных чисел на 3; 6
Угол
1.5
МВО
5.3.3.3 решать задачи на нахождение
градусной меры угла, на сравнение углов
Сравнение смешанных
1.6
МВО
5.1.2.16 сравнивать смешанные числа
чисел
Текстовые задачи
1.7
МВО
5.1.2.24 находить часть числа
Упрощение выражений
1.8
МВО
5.2.1.2 находить значения буквенного
выражения по заданным значениям букв
Действия над
2.1
РО
5.1.2.18 выполнять сложение, вычитание
обыкновенными
дробей с разными знаменателями
дробями
Действия над
2.2
РО
5.1.2.27 выполнять сложение, вычитание,
десятичными дробями
умножение и деление десятичных дробей
Процент
2.3
РО
5.5.1.6 решать текстовые задачи на проценты
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1 Выберите правильное равенство:
15.
A) 4 4 4 4 4 5 4B) 4 4 4 4 4 45
C) 4 4 4 4 4 4 5
D) 4 4 4 4 4 5 : 4
1.2 Решите уравнение: 144: (х+10)=12
A) 1
B) 3
C) 2
D) 0
Е) 4
1.3 Дано множество С={ 5, 6, 7, 8, 9, 10}. Составьте множество Д состоящее из трех
элементов, если известно что С ⊂ Д .
A) {4, 6, 10 }
B) {5, 9, 7 }
C) {3, 8, 9 }
D) {5, 3, 7 }
Е) {6, 2, 8 }
1.4. При каких значениях цифры * число 38577* будет делиться на 3?
A) 1
B) 3
C) 2
D) 5
Е) 4
1.5. Найдите значения неизвестного угла:
Примечание: НЕ использовать транспортир в этой задаче
С
D
37
?
А
О
В
A) 180
B) 53
C) 90
D) 73
Е) 35
1.6. Сравните смешанные числа:
A)
B)
C)
1.7 В школьную столовую привезли 120 кг картофеля. В первый день израсходовал
всего картофеля. Сколько картофеля израсходовали в первый день?
A) 85
B) 70
C) 95
16.
D) 90Е) 80
1.8. Упростите выражение: 4(11m+20) при m=2
A) 107
B) 115
C) 108
D) 105
Е) 118
Задания уровня В
2.1. Найдите значение выражения:
2 2 1
3
9 10 : 1
3 9 3
4
2.2. Найдите значение выражения:
2,66 : 1,4 27,09 24,5 1,02
2.3 Решить задачу:
Пачка гречневой крупы содержит 31% белков, 45% жиров, а остальные 48 г – углеводов.
Найди массу гречневой крупы.
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1 Выберите правильное равенство:
A) 2 2 2 2 2 5 2
B) 2 2 2 2 2 2 5
C) 2 2 2 2 2 25
D) 2 2 2 2 2 2 : 5
1.2. Решите уравнение: 121: (10+х)=11
A) 2
B) 3
C) 1
D) 0
Е) 4
1.3. Дано множество В ={3 ,4, 5, 6, 7, 8}. Составьте множество А, состоящее из трех
элементов, если известно что А ⊂ В.
A) {4, 6, 9 }
B) {5, 9, 7 }
C) {3, 8, 9 }
D) {5, 3, 7 }
Е) {5, 2, 8 }
1.4. При каких значениях цифры * число 38577* будет делиться на 3?
A) 1
B) 6
C) 2
D) 5
Е) 4
1.5. Найдите значения неизвестного угла:
17.
Примечание: НЕ использовать транспортир в этой задачеС
D
37
?
А
О
В
A) 180
B) 53
C) 90
D) 73
Е) 35
1.6. Сравните смешанные числа:
A)
B)
C)
1.7. В книге 120 страниц. Алеша прочитал
Алеша?
этой книги. Сколько страниц прочитал
A) 80
B) 95
C) 90
D) 70
Е) 85
1.8. Упростите выражение: 5(9n+20) при n=2
A) 170
B) 195
C) 190
D) 180
Е) 185
Задания уровня В
2.1. Найдите значение выражения:
1
2 3 3 1
6 : 20
4
3 7 4 7
2.2. Найдите значение выражения:
3,45 0,5 4,075 1,26 : 0,7
2.3 Решить задачу:
Сплав содержит 51% меди, 24% цинка, а остальные 32г – свинца. Найди массу сплава.
Критерий оценивания
№
Дескриптор
Балл
18.
Знает определение степенинатурального числа
Решает уравнения
задания
1.1
1.2
Записывает подмножество
данного множества.
Применяет признаки
делимости натуральных
чисел
1.3
Использует свойства углов,
для нахождения
неизвестных
Сравнивает смешанные
числа
Решает задачи на
нахождение части числа
1.5
Упрощает буквенные
выражения
1.8
1.4
1.6
1.7
Арифметические действия
2.1
над обыкновенными дробями
и смешанными числами
Арифметические действия
над десятичными дробями
Решает задачи на проценты
Итого
2.2
2.3
Записывает произведение одинаковых
чисел в виде степени
Применяет правило нахождения
неизвестного делителя и находит корень
уравнения
Находит подмножество данного
множества
Применяет признак делимости
натуральных чисел на 3 и находит
цифры, при которых выполняется
заданное условие.
Составляет выражение, используя
свойство развернутого угла и находит
значение угла
Сравнивает смешанные числа, приведя
дроби к общему знаменателю
Составляет выражение по условию
задачи и находит часть числа,
выполняет вычисления и находит ответ
Раскрывает скобки в
выражении,используя свойство
умножения, упрощает выражение,
используя свойство сложения
Выполняет деление обыкновенных
дробей и смешанных чисел
Выполняет умножение обыкновенных
дробей и смешанных чисел
Выполняет сложение обыкновенных
дробей и смешанных чисел
Выполняет вычитание обыкновенных
дробей и смешанных чисел
Выполняет деление десятичных дробей
Выполняет умножение десятичных
дробей
Выполняет сложение десятичных
дробей
Выполняет вычитание десятичных
дробей
Записывает краткую запись по условию
задачи
Находит число по его процентам
Выполняет вычисление и записывает
ответ
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
19
Комплексная диагностическая работа
по математике 6 класс 2021-2022 учебный год
авторы: Гапонова Ирина Борисовна, педагог-исследователь, Северо-Казахстанская
область, КГУ «Булаевская средняя школа№2» КГУ «Отдел образования района
М.Жумабаева» КГУ «Управление образования акимата Северо-Казахстанской области»
19.
Продолжительность – 45 минутТипы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задания
задания
Решение уравнений.
А1
МВО
5.2.2.1 - решать уравнения на основе правил
нахождения неизвестных компонентов
арифметических действий
Основное свойство
А2
МВО
5.1.2.14 - применять основное свойство дроби
дроби.
при сокращении обыкновенных дробей;
Действия с
А3
МВО
5.1.2.24 - находить часть числа и число по его
обыкновенными
части;
дробями
Нахождение части
А4
МВО
5.1.2.30 - выполнять деление десятичной
числа и числа по его
дроби на натуральное число и на десятичную
части
дробь;
Числовые и буквенные
А5
МВО
5.1.2.16 - приводить обыкновенные дроби к
выражения
общему знаменателю;
Деление десятичных
А6
МВО
5.2.1.2 - находить значения буквенного
дробей
выражения по заданным значениям букв;
Производить
В1
РО
5.5.1.4 – находить значения выражений
вычисления
помощью арифметических действий над
обыкновенных и
дробями
десятичных дробей
Решать задачи на
В2
РО
5.5.1.6 - решать текстовые задачи на проценты.
проценты
Вариант №1
Уровень А
А1. Решите уравнение:
1)3
2) 15
А2. Сократите дробь:
1)
3)3
4)5
5) 2
2)
А3. Вычислите:
1)
А4. Из 75 м ткани пошло на пошив платьев. Сколько метров ткани израсходовали на
платья?
1) 20
2) 40
3) 30 4) 50
5) 60
А5. Упростите выражение и найдите его значение:
1) 1,7
2)1,8
А6. Выполните деление:
1)3
2) 30
3) 17
4) 18
5) 20
3) 0,3
4) 300 5) 0,03
Уровень В
20.
В1. Выполните действия:В2. В первую неделю отремонтировали 96 моторов, после чего осталось выполнить 68%
месячного плана. Сколько моторов надо отремонтировать по плану?
Вариант №2
Уровень А
А1. Решите уравнение:
1)1
2) 9
3)7
А2. Сократите дробь:
1)
4)3
5) 11
2)
А3. Вычислите:
1)
А4. В классе 30 учеников. Из них составляют девочки. Сколько девочек в классе?
1) 20
2) 25
3) 30 4) 10
5) 15
А5. Упростите выражение и найдите его значение:
1) 1,6
2)12
А6. Выполните деление:
1)2,5
3) 16
2) 25
4) 1,2
3) 0,25
5) 1
4) 1,25
Уровень В
5) 250
В1. Выполните действия:
В2. Было отремонтировано 29% всех станков цеха, после чего осталось еще 142 станка.
Сколько станков в цехе?
Критерий оценивания
Определяет порядок действий в
выражениях со скобками
№
задания
А1
Выполняет сложение и вычитание
многозначных чисел
Выполняет деление многозначных
чисел на двузначное число, когда в
записи частного есть нули
А2
Выполняет сложение и умножение
при выполнении вычислений с
многозначными числами
А4
Находит значение выражения,
используя алгоритм умножения на
трехзначное число
Верно определяет выражение с
переменной при использовании их
А5
А3
А6
Дескриптор
Балл
Умеет определять порядок
действий в выражениях со
скобками
Применяет алгоритмы сложения и
вычитания многозначных чисел
Применяет алгоритмы деления
многозначных чисел на
двузначное число, когда в записи
частного есть нули
Применяет свойства сложения и
умножения при выполнении
вычислений с многозначными
числами
Применяет алгоритм умножения
на трехзначное число
1
Умеет составлять буквенное
выражение по условию задач
1
1
1
1
1
21.
для решения задачВ1
Выполняет действие деление в
правой части; и находит
неизвестное слагаемое
Находит неизвестный множитель
и записывает ответ
Определяет способ решения
задачи
Находит общее количество
молока
Выполняет решение уравнения
Верно составляет модель задачи и
решает задачи разными способами,
при этом определяет наиболее
рациональный
Итого:
В2
1
1
1
1
10
Комплексная диагностическая работа
по алгебре 7 класс 2021-2022 учебный год
автор: Бредихина Наталья Вячеславовна учитель математики и информатики,
педагог- эксперт КГУ «Афанасьевская средняя школа» КГУ «Отдел образования района
Шал акына» КГУ «Управления образования Северо-Казахстанской области»
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Отношения и
1.1
КО
6.1.2.5 знать и применять основное
пропорции
свойство пропорции
Действия над
рациональными
числами
Действия над
рациональными числами
Линейное уравнение с
одной переменной
1.2
РО
1.3
МВО
1.4
PО
6.1.2.18 распознавать, какие
обыкновенные дроби представимы как
конечные десятичные дроби
6.2.1.5 знать правила раскрытия
скобок
6.2.2.4 решать уравнения вида
х a b , где a и b – рациональные
Линейные неравенства с
одной переменной
1.5
РО
Статистика.
Комбинаторика
Линейные уравнения с
двумя переменными и их
системы
Линейные уравнения с
двумя переменными
1.6
МВО
1.7
КО
1.8
КО
Отношения и
пропорции
2.1
РО
числа
6.2.2.11 приводить неравенства с
помощью алгебраических
преобразований к неравенству вида
kx>b, kx≥b, kx<b, kx≤b
6.4.3.2 вычислять статистические
числовые характеристики
6.5.1.7 решать текстовые задачи с
помощью составления систем
линейных уравнений
6.2.2.16 знать определение линейного
уравнения с двумя переменными и его
свойства
6.5.1.2 решать задачи на проценты с
помощью пропорции
22.
Алгебраическиевыражения
2.2
РО
Алгебраические
выражения
2.3
РО
6.2.1.2 вычислять значения
алгебраических выражений при
рациональных значениях заданных
переменных
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Задана пропорция х : 20 = 2 : у. Найдите значение х·у.
A) -40
B) 40
C)4
D) -4
E) 10
1.2. Какую из данных дробей нельзя представить в виде конечной десятичной дроби?
А)1
Б) 3
В) 3
Г) 3
5
25
10
7
1.3. Раскройте скобки и приведите подобные слагаемые в выражении:
– (5,3a + 1,8b) + (0,5b – 1,3a) – (1,6b – 5,3a)
A) 1,3а – 2,9 b
B) -1,3а + 2,9 b
C) -1,3а – 2,9 b
D) 1,3а + 2,9 b
E) -1,3 b – 2,9а
1.4. Решите уравнение: 4|х|+5|х|-3=2|х|+11
A) х1=1 и х2=-1
B) х1=11/14 и х2=-11/14
C) х1=2 и х2=-2
D) х=-2
E) х=2
1.5. Приведите неравенство к виду kx ≥ b или kx≤ b:
A) х≤0,4
B) х≤-0,4
C) х>-0,4
D) х<-0,4
E) х<0,4
1.6. В кафе «Пицца» в течение 15 дней фиксировалось количество заказов с доставкой
на дом. Получили такой ряд данных: 39, 33, 45, 25, 33, 40, 47, 38, 34, 33, 40, 44, 45, 32,
27.
Найдите: Среднее арифметическое и Моду данного ряда
A) 37 и 38
B) 37 и 33
C) 39 и 27
23.
D) 38 и 34E) 37 и 45
1.7. Составьте систему уравнений к решению задачи :
За 2 кг мандаринов и 5 кг апельсинов заплатили 3200 тенге. Сколько стоит 1 кг
каждого вида фруктов, если 2 кг апельсинов на 1000 тенге дешевле, чем 3 кг
мандаринов?
A)
B)
C)
1.8 Какое из уравнений является линейным с двумя переменными
a) 2х2+ 3x + 5 = 0;
b) 3x + 2y + 1 = 0;
c) 4x + 3 = 0
d) 8+ 4x=0
e) 3x+5x2+1=0
Задания уровня В
2.1. Турист должен был пройти 60 км. В первый день он проехал 40% всего пути, во
второй день 50% оставшегося пути. Сколько километров ему осталось пройти? [4]
2.2. Найдите значение выражения:
0,72 3,6 0,28 3,6
[5]
1
2,4 : 0,04
2
2.3 Упростите выражение 1 2а 4 1 5b 6 и найдите его значение при a 2 1 , b 3
4
3
2
15
[3]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Задана пропорция 6 : х = у : 7. Найдите значение х·у.
A)-42
B) 48
C) -48
D) 6,7
E) 42
1.2 Какую из данных дробей нельзя представить в виде конечной десятичной дроби?
А) 1
Б) 4
В) 1
Г) 3
3
2
25
8
1.3. Раскройте скобки и приведите подобные слагаемые в выражении:
– (4,3a + 2,1b) + (0,4b – 3,3a) – (1,7b – 5,9a)
A) 1,7а – 3,4 b
B) -1,7а + 3,4 b
C) -1,7а – 3,4 b
D) 1,7а +3,4 b
24.
E) -17а – 3,4 b1.4. Решите уравнение: 7|х|-2|х|+6=3|х|+12
A) х=3
B х=-3
C) х1=3 и х2=-3
D) х1=6 и х2=-6
E) х=6
1.5. Приведите неравенство к виду kx ≥ b или kx≤ b:
A) х≥-11
B) х≥11
C) х<11
D) х<-11
E) х>11
1.6. В кафе «Горячие блюда» в течение 12 дней фиксировалось количество заказов с
доставкой на дом. 48; 53; 58; 47; 48; 62; 68; 48; 85; 90; 94; 97
Найдите: Среднее арифметическое и Моду данного ряда
A) 66,5 и 49
B) 66,5 и 48
C) 66,5 и 62
D) 48 и 62
E) 48 и 97
1.7 Составьте систему уравнений к решению задачи :
За 3 кг яблок и 6 кг апельсинов заплатили 4545 тенге. Сколько стоит 1 кг каждого вида
фруктов, если 2 кг яблок дешевле 3 кг апельсин на 1170 тенге?
A)
B)
C)
1.8 Какое из уравнений является линейным с двумя переменными
a) 12х2- 3x + 6 = 0;
b) 13x + y + 1 = 0;
c) 6x + 3 = 0
d) 4+ 4x=0
e) 3x+x2+1=0
Задания уровня В
2.1. В школе 240 учеников, из них 25% ученики начальной школы. Среди учеников
среднего и старшего звена 40% изучают немецкий язык, остальные французский. Сколько
учеников в школе изучают французский язык?
[4]
25.
0,58 1,8 0,42 1,8[5]
1
5,4 : 0,03
3
1
1
4а 2 5b 6 и найдите его значение при a 2 1 , b 4
6
5
4
5
2.2. Найдите значение выражения:
2.3 Упростите выражение
.
[3]
Критерий оценивания
Отношения и пропорции
№
Дескриптор
задания
1.1
Находит произведение х на у
Балл
1
Действия над
рациональными числами
Действия над
рациональными числами
Линейное уравнение с
одной переменной
Линейные неравенства с
одной переменной
Статистика.
Комбинаторика
Линейные уравнения с
двумя переменными и их
системы
Линейные уравнения с
двумя переменными
1.2
Определяет дробь
1
1.3
Упрощает выражение
1
1.4
Находит корни уравнения
1
1.5
Приводит неравенство к виду kx ≥ b или kx≤
b:
Находит первую и второю величину
1
1.7
Составляет систему уравнений к решению
задачи
1
1.8
1
Отношения и пропорции
2.1
Находит линейное уравнение с двумя
переменными
Составляет пропорцию, Находит из
пропорции х
Находит количество учеников среднего и
старшего звена
Составляет пропорцию, Находит из пропорции х
Находит количество учеников которые изучает
французский язык
Выносит общий множитель за скобки
Находит произведение десятичной дроби на
целое число
Находит произведение десятичной дроби на
обыкновенную дробь
Находит частное десятичной дроби на
десятичную дробь
Находит частное десятичной дроби на целое
число
Правильно раскрывает скобки
Приводит подобные слагаемые
Подставляет значения переменных, записывает
ответ
1
Алгебраические
выражения
Алгебраические
выражения
1.6
2.2
2.3
1
1
1
1
1
1
1
1
1
1
1
1
26.
Итого20
Комплексная диагностическая работа
по геометрии 7 класс 2021-2022 учебный год
автор: Жунусова Гульнар Сартаевна Педагог-модератор Павлодарская область
Щербактинский район Чигириновская СОШ
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Длина окружности.
1.1
МВО
6.3.3.3знать и применять формулу
длины окружности;
Площадь круга. Шар.
1.2
МВО
6.3.3.4знать и применять формулу
Сфера
площади круга;
Целые числа.
1.3
МВО
6.1.2.9изображать рациональные
Рациональные числа
числа на координатной прямой;
Модуль числа
1.4
МВО
6.3.3.1находить расстояние между
точками на координатной прямой;
Сложение рациональных
1.5
МВО
6.1.2.10выполнять сложение и
чисел с помощью
вычитание целых чисел с помощью
координатной прямой
координатной прямой;
Перпендикулярные прямые
и отрезки. Параллельные
прямые и отрезки
Координатная плоскость.
Прямоугольная система
координат
1.6
МВО
1.7
МВО
Центральная симметрия.
Осевая симметрия
1.8
МВО
Масштаб
2.1
РО
«Координатная плоскость»
2.2
РО
Прямая
пропорциональность и её
график
2.3
РО
6.3.2.2 распознавать
перпендикулярные, параллельные
прямые и отрезки;
6.3.1.4строить точку в системе
координат по ее координатам и
находить координаты точки, заданной
на координатной плоскости;
6.3.1.6 иметь представление о
фигурах, имеющих ось или центр
симметрии; распознавать
симметричные и центральносимметричные фигуры;
6.5.1.3применять масштаб при работе
с картой, планом, чертежом;
6.3.2.5 строить точки и фигуры,
симметричные относительно начала
координат и координатных осей в
прямоугольной системе координат;
6.5.2.12записывать формулу прямой
пропорциональности по описанию;
6.5.2.13строить график прямой
пропорциональности;
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
27.
1.1. Найдите длину окружности с диаметром MN, если M(–2; -2); N(1; 2).А) 15,7;
В)7,85;
С) 31,4;
Д) свой ответ
1.2. Найдите площадь круга, если его диаметр равен 6дм ?
A) 18,84
В) 28,26
С) 9,42
D) 18
E) 14,26
1.3 Между какими числами на координатной прямой расположено число 4,8
A) 4 и 6
B) 5 и 6
C) 4 и 5
D) 5 и 7
E) 4 и 7
1.4. Найдите расстояниее от точки А(-2) до точки В (5)
А) 3
В) 6
C) -7
D) 7
E) 8
1.5. Используя рисунок, вычислите координаты точки А
-4
A)5 9
B) 4
C) 7
D) 5
E) 1
1.6. Какой из отрезков АВ, АС или АD перпендикулярен прямой d?
А
В
С
D
d
28.
А)ABи ADB) ABи AC
C) AC и AD
D) AC и ВD
1.7. В какой четверти коорднатной плоскости находится точка А (1;-4)
A) 1
B) 2
C)3
D) 4
1.8. Определите какие из фигур являются симметричными фигурами
А)
В)
С)
D)
Е)
29.
А) A,EиDВ)В, СиЕ
C)B,Eи D
D)В,Cи E
E)А, Cи E
Задания уровня В
2.1. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности
в 72 км. Каково расстояние между городами, если на этой карте между ними 12,6 см?
2.2. Постройте на координатной плоскости отрезок ВС, где В(3; –2), С(–1; 1).
Постройте отрезок, симметричный отрезку ВС относительно оси абсцисс, и
определите координаты концов полученного отрезка.
2.3 Постройте график движения автомобиля со скоростью 50 км/ч
в течение 6 часов, если автомобиль выехал из города в 4 часа дня
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Найдите длину окружности с диаметром MN, если M(–1; 2); N(3; 2).
а) 6,28;
б) 12,56;
в) 25,12;
г) свой ответ
1.2. Найдите площадь круга, если его диаметр равен 4 дм ?
A) 12,34
В) 14,22
С) 12,56
D) 16
E) 14,26
1.3 Между какими числами на координатной прямой расположено число 5,3
A) 4 и 5
B) 4 и 7
C) 3 и 5
D) 5 и 6
E) 5 и 7
1.4. Найдите расстояниее от точки А(-3) до точки В (7)
А) 4
В) 5
C) -10
D) 7
E) 10
1.5. Используя рисунок, вычислите координаты точки А
30.
-6А
A) 8
B) 9
C) 10
D) -10
E) -8
-4
1.6.Какой из отрезковBC, BD или BE перпендикулярен прямой a?
B
С
D
E
a
А)BCи BD
B) BCи BE
C) BD и BE
D)СEи ВD
1.7. В какой четверти коорднатной плоскости находится точка А (-2;6)
A) 1
B) 2
C)3
D) 4
1.8 Определите какие из фигур являются симметричными фигурами
А)
В)
31.
С)Е)
D)
А) A,EиD
В)A,BиD
C)B,Eи D
D)В,Cи E
E)А, Cи E
Задания уровня В
2.1. Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на
карте длина отрезка, изображающего 10 км?
[4]
2.2. Постройте на координатной плоскости отрезок РЕ, где Р (–3; –1), Е (2; 3).
Постройте отрезок, симметричный отрезку РЕ относительно оси ординат, и
определите координаты концов полученного отрезка.
[3]
2.3 Постройте график движения автомобиля со скоростью 50 км/ч
в течение 7 часов, если автомобиль выехал из города в 2 часа дня
[2]
Критерий оценивания
Знает формулу длины окружности
Находит площадь круга
№
задания
1.1
1.2
Дескриптор
Балл
Находит длину окружности
Находит площадь круга,
используя формулу
Находит целые числа
Применяет определение модуля
1
1
1.5
Складывает целые числа с
помощью координатной прямой
1
1.6
Указывает перпендикулярные
прямые
Указывает четверть
1
Знает определение целых чисел
Вычисляет расстояние между точками
на координатной прямой
Использует координатную прямую при
сложении и вычитании рациональных
чисел
Распознает перпендикулярные прямые
1.3
1.4
Определяет положение точки на
1.7
1
1
1
32.
координатной плоскостиРаспознает фигуры,имеющие ось или
центр симметрии
Решает задачи,используя определение
масштаба
1.8
2.1
Определяет координаты
точек,симметричных относительно
осей координат
2.2
Записывает формулу прямой
пропорциональности по описанию,
строит график прямой
пропорциональности
2.3
Итого
координатной плоскости,
соответствующей точки
Определяет симметричные
фигуры
Переводит величины в одни
единицы измерения
Составляет отношение,используя
определение масштаба
Выполняет вычисления
Находит ответ
1
1
1
1
1
Отмечает точки на координатной 1
прямой
Определяет координаты точек
1
,симметричных относительно оси
ординат
Строит симметричные отрезки
1
Записывает формулу,
1
выражающую зависимость
пройденного пути от времени
движения
Строит график зависимости
1
16
Комплексная диагностическая работа
по математике 7 класс 2021-2022 учебный год
автор: Гапонова Ирина Борисовна, педагог-исследователь, Северо-Казахстанская
область, КГУ «Булаевская средняя школа№2» КГУ «Отдел образования района
М.Жумабаева» КГУ «Управление образования акимата Северо-Казахстанской области»
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задани задани
я
я
Основное свойство
А1
МВО
5.2.2.1 - решать уравнения на основе правил
пропорции.
нахождения неизвестных компонентов
арифметических действий
Действия над
А2
МВО
5.1.2.14 - применять основное свойство дроби при
рациональными
сокращении обыкновенных дробей;
числами.
Линейные уравнения
А3
МВО
5.1.2.24 - находить часть числа и число по его
части;
Линейные неравенства
А4
МВО
5.1.2.30 - выполнять деление десятичной дроби на
натуральное число и на десятичную дробь;
Системы уравнений с
А5
МВО
5.1.2.16 - приводить обыкновенные дроби к
двумя неизвестными
общему знаменателю;
33.
Решение неравенств смодулем
Выполнять вычисления
над рациональными
дробями
Решать задачи на
проценты
А6
МВО
В1
РО
В2
РО
5.2.1.2 - находить значения буквенного выражения
по заданным значениям букв;
5.5.1.4 – находить значения выражений помощью
арифметических действий над дробями
5.5.1.6 - решать текстовые задачи на проценты.
Вариант №1
Уровень А
А1. Дана пропорция 13:х =17: у. Какие из следующих равенств НЕ являются пропорцией?
1) х:у=13:17 2) 13 :у=17:х
3) х: 13 =у:17 4) у :х =17 :13
5) х:у =17:13
А2. Вычислите: -38 – (-15,6)
1) 21,4
2) -22,4 3) 22,4
4) -21,4
5) -2,24
А3. Решите уравнение: 5у +27 = 4у +21
1) -6
2) 6
3) - 48
4) 48 5) 8
А4. Решите неравенство: 4х +2
1)
) 2) (1;
3) ( -1;+
4) (1; +
5) (А5. Решить систему уравнений с двумя неизвестными:
1) (2;11) 2) (-2;11) 3) (-2;-11)
А6. Решите неравенство с модулем:
1) (3;1)
2) (-3;1)
3)
4) (2;-11) 5) (-1;-11)
4)
Уровень В
5)
В1. Выполните действия:
В2. Сначала продали 40% привезенного картофеля, а потом 30% остатка. Сколько
процентов привезенного картофеля осталось?
Вариант №2
Уровень А
А1. Дана пропорция 14:х =16: у. Какие из следующих равенств НЕ являются пропорцией?
2) х:у=14:16 2) 14 :у=16:х
3) х: 14 =у:16 4) у :х =16 :14
5) х:у =16:14
А2. Вычислите: -36,7 – (-9,6)
2) 27,1 2) -2,71 3) -27,1 4) 2,71
5) -2,17
А3. Решите уравнение: 2х - 12= 5х +15
1) -9
2) 9
3) - 27
4) 27 5) 8
А4. Решите неравенство: 2х +1
2)
) 2) (5;
3) ( -5;+
4) (7; +
5) (А5. Решить систему уравнений с двумя неизвестными:
2) (13;2) 2) (-13;2) 3) (-13; -2))
А6. Решите неравенство с модулем:
2) (3;1)
2) (-1;3)
В1. Выполните действия:
3)
4) (2;-11) 5) (-2;-11)
4)
5)
Уровень В
34.
В2. Сначала Витя прочитал 60% всей книги, а потом 40% остатка. Сколько процентовкниги осталось прочитать Вите?
Критерий оценивания
Определяет верные и не верные
пропорции
№
задания
А1
Выполняет сложение и вычитание
рациональных чисел
А2
Решает линейное уравнение
А3
Решает линейные неравенства
А4
Решает систему уравнений с двумя
неизвестными одним из способов
( сложения или подстановки)
Находит интервал решения
неравенства с модулем
А5
Выполняет вычисления
рациональных дробей
Верно составляет модель задачи и
решает задачи разными способами,
при этом определяет наиболее
рациональный способ
Итого:
А6
В1
В2
Дескриптор
Балл
Знает основное свойство
пропорции и применяет
процессе решения
Применяет правила сложения
чисел с разными и
одинаковыми знаками
Применяет алгоритмы решения
линейных уравнений
Применяет алгоритм решения
линейных неравенств и
изображает решение на
координатном луче
Применяет один из способов
решения систем уравнений с
двумя неизвестными
Умеет решать неравенство
вида
Умеет вычитать рациональные
дроби
Умеет умножать дробь на число
Составляет пропорцию
Выполняет решение, находит
ответ
1
1
1
1
1
1
1
1
1
1
10
Комплексная диагностическая работа
по алгебре 8 класс 2021-2022 учебный год
Авторы : Кузьмина Инга Валерьевна, учитель физики и математики, Костанайская
область, КГУ «Новоселовская основная средняя школа отдела образования Карасуского
района» Управления образования акимата Костанайской области. Категория : педагог –
исследователь.
Романенко Наталья Ивановна, учитель математики, КГУ «Петропавловская средняя
школа»
государственного
учреждения
«Отдел образования Каргалинского района
Управления образования Актюбинской области». Категория : высшая.
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задания задания
35.
Многочлены1.1
МВО
7.2.1.2 знать определение одночлена, находить его
коэффициент и степень
7.1.2.15 применять свойства степени с натуральным
показателем
7.2.1.1 применять свойства степени с целым
показателем при нахождении значений числовых
выражений
7.4.1.12 строить график функции
и знать
Степень с целым
показателем
1.2
МВО
1.3
МВО
Функция. График
функции
1.4
МВО
Элементы
статистики
Формулы
сокращённого
умножения
1.5
МВО
1.6
МВО
1.7
МВО
Алгебраические
дроби
1.8
МВО
Разложение
многочлена на
множители
2.1
РО
7.2.1.13 выполнять тождественные преобразования
алгебраических
выражений с помощью действий
над многочленами, разложение многочлена на
множители
Функция. График
функции
Действия с
алгебраическими
дробями
2.2
РО
2.3
РО
7.4.2.4 решать системы линейных уравнений
графическим способом
7.2.1.19 выполнять сложение и вычитание
алгебраических дробей
7.2.1.20 выполнять умножение и деление, возведение в
степень алгебраических дробей
её свойства
7.3.3.2 вычислять абсолютную и относительную
частоты варианты
7.2.1.11 знать и применять формулы сокращённого
умножения
7.1.2.14
использовать формулы сокращённого умножения для
рационального счёта;
7.2.1.18 применять основное свойство алгебраической
дроби
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1 Определите коэффициент и степень одночлена
A)
B)
и8
и9
C)
и9
D)
и9
36.
E)13 и 8
1.2 Вычислите:
A)
B)
C)
D)
E)
1.3 Упростите:
A)
B)
C)
D)
E)
1.4
Найдите значение коэффициента k, если известно, что график функции y
k
x
проходит через точку с координатами M ( 2;3)
A) -6
B)
C) 6
D) 1
E) -1
1.5
В тестировании принимали участие учащиеся 8 класса. Для проведения
статистического исследования был записан результат каждого учащегося: 20, 17, 16, 11,
18, 17, 20, 11, 18, 16, 19, 18, 11, 19, 20. Определите абсолютную и относительную частоту
результата тестирования, соответствующего 20 баллам.
A) 2 и
B) 3 и
C) 3 и
D) 2 и
E) 3 и
1.6 Возведите в куб сумму 5х+1
A) 25х3+125х2+25х+1
B) 25х3+75х2+15х+1
C) 125х3+75х2+15х+1
D) 125х3+75х2+3х+1
E) 5х3+75х2+15х+1
1.7 Вычислите: 252-50∙17+172
37.
A)B)
C)
D)
E)
625
850
64
8
1764
1.8 Сократите дробь:
A)
;
B)
;
C)
;
D)
;
E)
Задания уровня В
2.1 Разложить на множители : х + 4х2 + 4х + 16
3
2.2 Решить систему уравнений графическим способом:
2.3 Выполнить действия :
–
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
Определите коэффициент и степень одночлена
A.1
A)
B)
и6
и6
C)
и7
D)
и6
E)
16 и 8
A.2 Вычислите:
A)
B)
C)
D)
E)
A.3 Упростите:
A)
38.
B)C)
D)
E)
A.4 Найдите значение коэффициента k, если известно, что график функции y
проходит через точку с координатами M ( 3;4)
A) -12
B)
C) 12
D) 1
E) -1
A.5 В тестировании принимали участие учащиеся 8 класса. Для проведения
статистического исследования был записан результат каждого учащегося: 20, 15, 16,
11, 18, 17, 20, 15, 15, 16, 19, 18, 15, 19, 20. Определите абсолютную и относительную
частоту результата тестирования, соответствующего 15 баллам.
A) 2 и
B) 4 и
C) 4 и
D) 15 и
E) 4 и
A.6 Возведите в куб сумму 4х+1
A) 64х3+4х2+12х+1
B) 16х3+12х2+3х+1
C) 64х3+12х2+4х+1
D) 64х3+48х2+12х+1
E) 16х3+48х2+3х+1
A.7 Вычислите: 162-32∙12+122
A) 784
B) 16
C) 28
D) 4
E) 384
A.8 Сократите дробь:
A)
B)
C)
k
x
39.
D)E)
Задания уровня В
2.1 Разложить на множители: х – ху -2х+ 2у
2
2.2 Решить систему уравнений графическим способом:
2.3 Выполнить действия :
Критерий оценивания
Определяет коэффициент и
степень одночлена
Применяет свойства степени с
натуральным показателем для
преобразования выражения
№
задания
1.1
1.2
Применяет свойства степени с
целым показателем при
нахождении значений числовых
выражений
Вычисляет значение
коэффициента k функции
k
y , проходящей через
x
заданную точку
Находит абсолютную и
относительную частоты
варианты
Применяет формулу
сокращенного умножения для
преобразования выражения
1.3
Использует формулы
сокращённого умножения для
рационального счёта
Применяет основное свойство
алгебраической дроби
Раскладывает алгебраическое
выражение на множители,
используя способ группировки
1.7
Находит решение систем
2.2
1.4
1.5
1.6
1.8
2.1
+
Дескриптор
Балл
Находит коэффициент и вычисляет степень
одночлена
Выполняет преобразование выражения
используя свойства степени с натуральным
показателем: возведение степень в степень,
умножение степеней с одинаковым основанием
Находит значение числового выражения,
используя свойства степени
1
Определяет зависимость коэффициента k от
переменных у и х. Вычисляет значение
k
коэффициента k функции y , проходящей
x
через заданную точку
Вычисляет абсолютную и относительную
частоту варианты
1
Составляет выражение согласно условию
задания и применяет формулу куба суммы двух
выражений, преобразовывает полученное
выражение
Применяет формулу квадрата разности двух
выражений для преобразования данного
выражения
Сокращает дробь, используя основное свойство
алгебраической дроби
Использует метод группировки
Выносит общий множитель за скобки
1
Выполняет разложение на множители
1
Выражает переменную у через х в первом
1
1
1
1
1
1
1
1
40.
уравнений графическимспособом
Выполняет действия с
алгебраическими дробями
Итого
2.3
уравнении системы
Выражает переменную у через х во втором
уравнении системы
Выполняет построение графиков функций в
одной системе координат;
Находит абсциссу и ординату точки
пересечения;
Записывает ответ
Определяет порядок действий
Выполняет умножение/деление дробей
Приводит дроби к общему знаменателю
Выполняет сложение/вычитание дробей
1
1
1
1
1
1
1
1
20
Комплексная диагностическая работа
по геометрии 8 класс 2021-2022 учебный год
Авторы: Куатбекова Алмагуль Саламатовна, Карагандинская область БухарЖырауский район КГУ«Общеобразовательная школа имени Талгата Бигелдинова»
отдела образования Бухар-Жырауского района управления образования Карагандинской
области, педагог-эксперт
Стурова Ольга Анатольевна, Жамбылская область Таласский район г. Каратау КГУ
«ШКОЛА ЛИЦЕЙ №1 отдела образования Таласского района управления образования
акимата Жамбылской области», категория высшая
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Аксиомы и теоремы
1.1
МВО
7.1.2.1 знать и применять аксиомы
расположения точек на прямой и на
плоскости (аксиома порядка);
Свойства смежных и
1.2
МВО
7.1.1.10 доказывать и применять
вертикальных углов
свойства вертикальных и смежных
углов;
Медианы, биссектрисы,
1.3
МВО
7.1.1.12 знать определение медианы,
высоты треугольника
биссектрисы, высоты,
треугольника и изображать их;
Признаки равенства
1.4
МВО
7.1.1.22
применять
признаки
треугольников
равенства
треугольников
при
решении задач на вычисление и на
доказательство;
Признаки параллельности
1.5
МВО
7.1.2.5
применять
признаки
прямых
параллельности прямых при решении
задач;
Сумма углов треугольника.
1.6
МВО
7.1.1.17 применять теорему о сумме
41.
Неравенство треугольника1.7
МВО
Окружности, описанная
около треугольника и
вписанная в треугольник
1.8
МВО
Свойства параллельности
прямых
2.1
РО
Свойства прямоугольного
треугольника
Внешний угол
треугольника
2.2
РО
2.3
РО
внутренних углов треугольника и
следствия из неё при решении задач;
7.1.1.20 знать соотношение между
сторонами и углами треугольника и
применять его при решении задач;
7.1.2.14
знать
определения
окружностей,
вписанной
в
треугольник и описанной около
треугольника;
7.1.2.7 применять свойства
параллельных прямых при решении
задач
7.1.1.27 применять свойства
прямоугольного треугольника
7.1.1.19 применять теорему о
внешнем угле треугольника
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое задание оценивается в 1 балл.
1.1. Точка С лежит на отрезке АВ. Сравните длины отрезков
А) АС > АВ
В) CB=AB
С) АВ <СВ
D) АВ =АС
E) СВ < АВ
1.2. Чему равен угол между биссектрисами смежных углов?
A) 600
B) 900
C) 1000
D) 450
E)1800
1.3 В треугольнике АВС АК - медиана, ВК= 4,6 см. Чему равна длина отрезка КС?
A) 6,9 cм
В) 2,3 см
C) 9,2 см
D) 4,6 см
E) 4 см
1.4. Выберите признак равенства треугольников на рисунке.
A) по двум сторонам и углу между ними
B) по стороне и двум прилежащим к ней углам
42.
C) по трем сторонамD) по стороне и двум углам
E) по трем углам
1.5. Две прямые пересечены секущей. Чему равна сумма внутренних односторонних
углов, если внутренние накрест лежащие углы равны?
A) 1800
B) 900
C) 00
D) 600
E) 300
1.6. Найдите 1, 2, 3.
А) 60◦, 60◦, 60
B) 35◦, 110◦,35◦
C) 20◦, 80◦, 80◦
D) 30◦, 30◦, 120◦
E) 500; 650; 650
1.7. Найдите самый маленький угол в треугольнике АВС, если АВ < АС < ВС.
А) С
B) В
C) А
D) все углы равны
E) невозможно определить
1.8. Окружность называется вписанной в треугольник, если она…
A) пересекает его стороны;
B) проходит через его вершины;
C) касается одной стороны;
D) проходит через одну из вершин;
E) касается всех его сторон.
Задания уровня В
2.1. Прямые m и n параллельны. Найдите ∠3, если ∠1=48 , ∠2=57 . [4]
2.2 В AMD :
Найдите:
DAM
, МС – биссектриса , DCM = 63°.
[3]
43.
2.3 Найдите х[3]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое задание
оценивается в 1 балл.
1.1. Точка В лежит на отрезке АС. Сравните длины отрезков:
А) АС > АВ
B) СВ < АC
C) АВ < СВ
D) АВ = АС
E) BC = AC
1.2. Найдите угол между биссектрисами вертикальных углов?
A) 450
B) 900
C) 1800
D) 600
E) 1200
1.3. В треугольнике КМС КР- биссектриса, угол МКС = 780. Чему равна градусная мера
угла МКР?
A) 900
B) 780
C) 360
D) 1560
E) 390
1.4. По какому признаку равны треугольники на рисунке?
A) по двум сторонам и углу между ними
B) по стороне и двум прилежащим к ней углам
C) по трем сторонам
D) по стороне и двум углам
E) по трем углам
44.
1.5. Сумма внутренних накрест лежащих углов при параллельных прямых и секущейравна 2200. Чему равны эти углы?
A) 1800
B) 900
C) 1100
D) 2200
E) 1000
1.6. Найдите 1, 2, 3.
А) 40◦,100◦, 40◦
B) 420◦, 20◦, 140◦
C) 60◦,40◦, 80◦
D) 30◦,30◦, 120◦
E) 20◦, 80◦, 80◦
1.7. Найдите самый больший угол в треугольнике АВС, если АВ < АС < ВС.
А) С
B) В
C) А
D) все углы равны
E) невозможно определить
1.8. Окружность называется описанной около треугольника, если она…
A) пересекает его стороны;
B) проходит через его вершины;
C) касается его сторон;
D) проходит через одну из вершин;
E) проходит через две вершины.
Задания уровня В
2.1. Прямые m и n параллельны. Найдите ∠3, если ∠1=36 , ∠2=75 . [4]
2.2 В AMD :
Найдите:
DAM
, МС – биссектриса , DCM = 72°.
[3]
45.
2.3 Найдите х[3]
84
Критерий оценивания
Сравнивает длины отрезков
№
задания
1.1
Определяет угол между
биссектрисами
1.2
Находит длину отрезка
(находит градусную меру
угла)
Выбирает признак равенства
треугольников
1.3
Вычисляет сумму углов при
параллельных прямых и
секущей
Находит углы треугольника
1.5
Определяет меньший
(больший) угол в
треугольнике
Знает определения
окружностей, вписанной в
треугольник и описанной
около треугольника;
Находит неизвестный угол,
используя свойства
параллельных прямых
1.7
1.4
1.6
1.8
2.1
Дескриптор
Балл
Применяет аксиомы расположения
точек на прямой и сравнивает длины
отрезков
Применяет свойства вертикальных и
смежных углов и находит угол между
биссектрисами
Использует определения медианы и
биссектрисы треугольника и находит
длину отрезка и величину угла
Знает признаки равенства
треугольников и может по рисунку дать
правильный ответ
Применяет признаки параллельности
прямых при решении задач и вычисляет
сумму углов
Применяя теорему о сумме внутренних
углов треугольника и следствия из нее
и свойства равнобедренного
треугольника, находит углы
треугольника
Знает соотношение между сторонами и
углами треугольника и применяет его
при решении задачи
Использует определения окружностей,
вписанной в треугольник и описанной
около треугольника и делает
правильный выбор
Находит градусную меру вертикального
угла
Находит градусную меру накрест
лежащего угла
Определяет развернутый угол и его
градусную меру
Находит неизвестный угол
1
1
1
1
1
1
1
1
1
1
1
1
46.
Использует свойствапрямоугольного
треугольника для
нахождения неизвестных
углов
Использует теорему о
внешнем угле треугольника
2.2
2.3
Итого
Находит неизвестный угол MCD
Использует определение биссектрисы
угла и находит М
Находит искомый угол треугольника
1
1
Определяет вид KON
Применяет теорему о внешнем угле
треугольника, находит сумму углов
Находит значение х
1
1
1
1
18
Комплексная диагностическая работа
по алгебре 8 класс 2021-2022 учебный год
автор: Черненко Наталья Дмитриевна, педагог-исследователь, Северо-Казахстанская
область, КГУ «Воскресеновская средняя школа» КГУ «Отдел образования Мамлютского
района» КГУ «Управление образования акимата Северо-Казахстанской области»
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задания задания
Степень
с
целым А1
МВО
7.1.2.15 применять свойства степени с
показателем
натуральным показателем
Формулы
А2
МВО
7.2.1.10
знать и применять формулы
сокращённого
сокращённого
умножения
умножения
Многочлены.
А3
МВО
7.2.1.6
приводить
многочлен
к
стандартному виду;
7.2.1.11 знать и применять формулы
сокращённого
умножения
Линейная функция и её А4
график
Одночлены и действия А5
над ними
Вариационные ряды
А6
МВО
Преобразования
В1
выражений с помощью
формул сокращённого
умножения
Тождественные
В2
преобразования
РО
МВО
МВО
РО
7.4.1.5
знать
определение
линейной
функции
7.2.1.3 записывать одночлен в стандартном
виде;
7.3.3.1
усвоить понятия генеральной
совокупности,
случайной
выборки,
вариационного ряда, варианты;
7.2.1.15
выполнять
тождественные
преобразования алгебраических выражений
с
помощью
формул
сокращённого
умножения;
7.2.1.21
выполнять
преобразования
алгебраических выражений;
47.
алгебраическихвыражений
1 вариант
А1. Упростите выражение:
1)
2) a14
3) a 40
4) a39
5) a41
А2. Разложить на множители: 49-81d2
1)
(7 – 81d)(7 + 81d) 2) (49 – 81d)(49 + 81d) 3) (7 -9d)(7 + 9d) 4)(49 – 9d)(49 + 9d) 5)
А3. Преобразуйте в многочлен стандартного вида: (4b2 + 6ab + 9b2)(2a – 3b)
2) (2a-3b)2 2)
3) (2a+3b)2 4)(2a)3-(3b)3
5)
А4. Какие из точек А(0;4), В(1;8), С(2;-2,8), Д(10, -11,6), Е(-5;6,4) принадлежат графику
линейной функции: y= -1,2х + 0,4
1) А 2) В 3) С 4) Д
5) Е
А5. Упростите выражение: 100x6y3÷25x4y, и найдите его значение при x=3, y= 1) 4х²у², 9
2) 4х10у4 , 4380
3) х²у²,
4)75ху, -
5) 4х²у², - 9
А6. Чему равна разность между наибольшим и наименьшим значением варианты
ряда: 3º;7º; 1º; 4º; 0º; 5º; 1º; 3º; 6º; 4º; 9º; 2º
1) 8
2) 9
3) 7
4)1
5) 5
Уровень В
В1. Решить уравнение: 5(х-4)² -(х+5)²=4х²+5
В2. Упростить выражение: (
)(1 -
)
2 вариант
А1. Упростите выражение:
1)
2) c4
3) c 7
4) c12
5) c22
А2. Разложить на множители: 100a²-36b2
1)(100a –6b)(100a + 6b) 2) (10a –36b)(10a + 36b) 3) (10a -6b)(10a + 6b) 4)(100a – 36d)(100a + 36d)
5)
А3. Преобразуйте в многочлен стандартного вида: (4b2-6ab+9b2)(2a+3b)
2) (2a-3b)2 2)
3) (2a+3b)2 4)(2a)3 + (3b)3
5)
А4. Какие из точек А(0; 4), В(1; 8), С(2;-2,8), Д(10, -12,4), Е(-5;6,4) принадлежат графику
линейной функции: y= -1,2х-0,4
1) А
2) В
3) С
4) Д
5) Е
А5. Упростите выражение: 75x6y3÷15x4y, и найдите его значение при x=10, y= 2) 5х²у², 20
2) 5х10у4 , 4380
3) х²у²,
4) 5ху, -
5) 5х²у², - 20
А6. Чему равна разность между наибольшим и наименьшим значением варианты
ряда: 3º;7º; 1º; 4º;4 ; 5º; 1º; 3º; 6º; 4º; 9º; 2º;8º
3) 9
2) 8
3) 7
4)1
5) 5
Уровень В
В1. Решить уравнение: 4(х+3)² -(х+2)²=3х² -8
48.
В2. Упростить выражение: (Критерий оценивания
Применяет свойства степени
с натуральным показателем
для упрощения выражения
Применяет формулу
сокращенного умножения
для разложения выражения
на множители
Преобразует выражение в
многочлен стандартного
вида
Определяет, какие из точек
принадлежат графику
линейной функции
Выполняет деление
одночленов, находит
значение одночлена при
заданных значениях
переменных
Вычисляет разность между
наибольшим и наименьшим
значением варианты ряда
Решает уравнение
Выполняет упрощение
алгебраических дробей
)(
№
задания
А1
А2
А3
А4
А5
А6
В1
В2
)
Дескриптор
Балл
упрощает выражение, используя свойства
степени с натуральным показателем:
возведение степень в степень, умножение и
деление степеней с одинаковым
основанием
представляет в виде произведения,
используя формулу разности квадратов
1
Представляет выражение в виде
многочлена стандартного вида, используя
формулу разности кубов
Определяет, какие из точек принадлежат
графику линейной функции
1
Упрощает выражения, используя правило
деления одночленов, свойства степени с
натуральным показателем, и вычисляет
значение одночлена при заданных
значениях переменных
Находит наибольшую и наименьшую
варианту, и вычисляет их разность.
1
Применяет формулу квадрата
суммы(разности) двух выражений,
раскрывает скобки
1
Упрощает выражение и находит корень
уравнения
Выполняет сложение и вычитание
алгебраических дробей
Выполняет умножение алгебраических
дробей
1
1
1
1
1
1
Комплексная диагностическая работа
по алгебре 9 класс 2021-2022 учебный год
автор: Ткаченко Е.Ю. Костанайская область, г.Рудный, КГУ "Общеобразовательная
школа № 1 отдела образования города Рудного" Управления образования акимата
Костанайской области, педагог-эксперт
Продолжительность – 45 минут
Типы заданий:
МВО
–
задания
с
множественным
выбором
ответов;
РО – задания, требующие развернутого ответа
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
49.
Квадратные корни ииррациональные
выражения
Преобразования
выражений, содержащих
квадратные корни
Решение квадратных
уравнений
Решение квадратных
уравнений
Квадратный трёхчлен
1.1
МВО
8.1.2.1применять свойства
арифметического квадратного корня;
1.2
МВО
8.1.2.4 освобождать от
иррациональности знаменатель дроби
1.3
МВО
8.2.2.3 решать квадратные уравнения;
1.4
МВО
8.2.2.4 применять теорему Виета;
1.5
МВО
Решение уравнений
1.6
МВО
Решение уравнений
1.7
МВО
Квадратичная функция и
её график
1.8
МВО
Решение систем
неравенств
2.1
РО
Решение уравнений
2.2
РО
Решение текстовых
задач
2.3
РО
8.2.1.3 раскладывать квадратный
трехчлен на множители;
8.2.2.5 решать уравнения вида
|ax2+bx|+c=0; ax2+b|x|+c=0;
8.2.2.6 решать дробно-рациональные
уравнения;
8.4.1.3 знать свойства и строить график
квадратичной функции вида
;
8.2.2.10 решать системы из двух
неравенств, одно из которых линейное, а
второе – квадратное;
8.2.2.7 решать уравнения, приводимые к
квадратным уравнениям;
8.4.2.2 решать текстовые задачи с
помощью дробно-рациональных
уравнений;
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Какие свойства необходимо применить, чтобы преобразовать данное выражение:
1)
2)
3)
4)
5)
A) 1,2,3
B) 1,2,4
C) 1,2,5
D) 2,3,4
E) 1,2,3,4,5
1.2. Освободитесь от иррациональности в знаменателе дроби.
А)
50.
В)С)
D) х – 3
Е) х + 3
1.3. Найдите корни уравнения: 5х2 – 9х – 2 = 0
А) 2
В) -0,2
С) 2 и –0,2
D) – 2 и 0,2
E) нет решения
1.4. Если х₁ и х₂ - корни уравнения х² - 3х – 3 = 0, то найдите значение
выражения
А) - 27
В) 27
С)
D)
E)
1.5. Разложите квадратный трехчлен на множители: -х2+ 13х – 42 = 0
А) (х-6)(х-7)
В) (х+6)(х-7)
С) (х-6)(х+7)
D)(x+6)(x+7)
E)(6-x)(x-7)
1.6. Найдите корни уравнения: x2+|x|-6=0
А)
В)
С)
D)
E)
1.7. Найдите корни уравнения:
А) 1,5 и 2
В) 1,5
С) 2
D) - 2
E) 0
1.8. Определите координаты вершины параболы, используя формулы:
2х2 +8х +9 = 0
А) (-2;1)
В) (2;33)
С) (-2;-1)
D) (2;-33)
Е) (2;-1)
51.
Задания уровня В2.1. Решите систему неравенств:
[4]
2.2. Решите биквадратное уравнение: 9x4+5x2-4=0 [3]
2.3 Решите задачу с помощью дробно-рационального уравнения: [5]
Турист проплыл на лодке 3 км по течению реки и 2 км против течения реки за 30 минут.
Найти скорость лодки в стоячей воде, если скорость течения реки 2км/ч.
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Какие свойства необходимо применить, чтобы преобразовать данное выражение:
1)
2)
3)
4)
5)
A) 1,2,3
B) 1,2,4
C) 1,2,5
D) 2,3,4
E) 1,2,3,4,5
1.2. Освободитесь от иррациональности в знаменателе дроби.
А)
В)
С)
D)
Е)
1.3. Найдите корни уравнения: 7х2 – 5х – 2 = 0
А) 1
В)
С) 1 и
D) – 1 и
E) нет решения
52.
1.4. Если х₁ и х₂ - корни уравнения х² - 2х – 2 = 0, то найдите значениевыражения
А) - 4
В) 4
С)
D)
E)
1.5. Разложите квадратный трехчлен на множители: -х2+ 12х – 35 = 0
А) (х-5)(х-7)
В) (х+5)(х-7)
С) (х-5)(х+7)
D)(5-х)(x+7)
E)(x+5)(x-7)
1.6. Найдите корни уравнения: x2-8|x|+12=0
А)
В)
С)
D)
E)
1.7. Найдите корни уравнения:
А) 8,5 и - 5
В) 8,5
С) 5
D) - 5
E) – 8,5
1.8. Определите координаты вершины параболы, используя формулы:
х2+4х – 21 = 0
А) (-2;25)
В) (2;9)
С) (-2;9)
D) (-2;-25)
Е) (2;-25)
Задания уровня В
2.1. Решите систему неравенств:
[4]
2.2. Решите биквадратное уравнение: 4x4+3x2-1=0 [3]
2.3 Решите задачу с помощью дробно-рационального уравнения: [5]
Пароход прошёл 60 км по течению реки и затем обратно, затратив на весь путь 8 часов.
Требуется определить собственную скорость парохода, если скорость реки течения реки 4
км/ ч.
Критерий оценивания
№
Дескриптор
Балл
задания
Применяет свойства
1.1
Выбирает свойства для
1
53.
арифметического квадратного корняПреобразовывает выражение,
содержащее арифметический корень
1.2
Решает квадратные уравнения
1.3
Применяет теорему Виета
1.4
Раскладывает квадратный трехчлен
на множители
Решает уравнение вида
| ax2+b|x|+c=0;
Решает дробно-рациональные
уравнения
1.5
Знает
свойства
функции вида
1.6
1.7
квадратичной 1.8
;
Решение систем неравенств
2.1
Решает уравнения, приводимые к
квадратным уравнениям;
2.2
решает текстовые задачи с помощью
дробно-рациональных уравнений
2.3
Итого
преобразования выражения
Освобождается от
иррациональности знаменатель
дроби
Использует формулы корней
квадратного уравнения и находит
корни
Использует теорему Виета для
нахождения значения выражения
Находит корни уравнения и
раскладывает на множители
Находит корни уравнения
1
1
1
1
1
Использует алгоритм решения
дробно рационального уравнения,
находит корни
Использует формулы для
нахождения вершины параболы
1
Решает линейное неравенство
Решает квадратное неравенство
Показывает решение обоих
неравенств на числовых прямых
Находит общее решение системы
Вводит замену переменной
Решает квадратное уравнение
Возвращается к замене и находит
корни
вводит обозначение и связывает его
с другими величинами
составляет уравнение по условию
задачи
решает полученное уравнение
исключает лишние корни;
записывает ответ на вопрос задачи.
1
1
1
1
1
1
1
1
1
1
1
1
1
20
Комплексная диагностическая работа
по геометрии 9 класс 2021-2022 учебный год
автор: Сабитова Сулушаш Аймаковна, учитель математики 1 категории КГУ
«Средняя школа №18» отдела образования по городу Усть-Каменогорску управления
образования Восточно-Казахстанской области
Продолжительность – 45 минут
Типы заданий:
МВО
–
задания
с
множественным
выбором
ответов;
РО – задания, требующие развернутого ответа
Характеристика заданий
№
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
54.
Сумма внутренних угловмногоугольника. Сумма
внешних углов
многоугольника.
Параллелограмм,
прямоугольник, ромб,
квадрат, их свойства и
признаки.
1.1
МВО
8.1.1.2 выводить формулы суммы
внутренних углов и суммы внешних
углов многоугольника
1.2
МВО
3
Теорема Фалеса
1.3
МВО
4
Трапеция.
Равнобедренная и
прямоугольная трапеции
и их свойства.
Средняя линия
треугольника.
1.4
МВО
8.1.1.6 знать определение
прямоугольника, ромба и квадрата,
выводить их свойства и признаки
8.1.1.4 выводить и применять
свойства
параллелограмма
8.1.1.7 знать и применять теорему
Фалеса
8.1.1.11 знать определение, виды и
свойства трапеции
1.5
МВО
6
Средняя линия трапеции.
1.6
МВО
7
Свойство медиан
треугольника.
Замечательные точки
треугольника
Прямоугольная система
координат на плоскости
1.7
МВО
1.8
МВО
Площадь
квадрата,прямоугольника
и ромба
10 Площадь треугольника и
трапеции
2.1
РО
2.2
РО
11 Теорема Пифагора
2.3
РО
1
2
5
8
9
8.1.1.12 доказывать и применять
свойство средней линии
треугольника
8.1.1.13 доказывать и применять
свойство средней линии трапеции
8.1.3.1 знать и применять свойства
медиан, биссектрис, высот и
серединных перпендикуляров к
сторонам треугольника
8.1.3.17 знать уравнение окружности с
центром в точке (a,b) и радиусом r:
8.1.3.11 выводить и применять
формулы площади квадрата,
параллелограмма, ромба
8.1.3.12 выводить и применять
формулы площади треугольника
8.1.3.13 выводить и применять
формулы площади трапеции
8.1.3.3 доказывать и применять
теорему Пифагора;
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.2. Чему равна сумма внутренних углов правильного пятиугольника?
A) 6300
B) 5400
C) 4500
D) 3600
E) 1800
1.2. Сторона ромба равна 16,5 дм. Вычислите его периметр
55.
A) 46B) 86
C) 76
D) 66
E) 56
1.3. Прямая CD параллельна к AB и пересекает угол BOA так, что O,B,D лежат на одной
прямой, а также O,A,C лежат на одной прямой. Если AB=5, OB=3 и OD=12, найдите
длину CD.
A) 10
B) 15
C) 20
D) 25
E) 30
1.4. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит
большее основание на отрезки 10 и 20. Найти отношение ее оснований
A) 1:3
B) 1:5
C) 2:3
D) 2:5
E) 3:5
1.5. Дан треугольник, стороны которого 10 см, 6 см, 8 см. Найти периметр треугольника,
вершинами которого являются середины сторон данного треугольника.
A) 13
B) 12
C) 11
D) 10
E) 14
1.6. Средняя линия равнобедренной трапеции равна 30, верхнее основание – 17. Найдите
длину основания трапеции.
A) 53
B) 63
C) 33
D) 23
E) 43
1.7. Высота равностороннего треугольника 4,2 см. Найдите расстояние от точки
пересечения биссектрисс треугольника до его стороны.
A) 1,1
B) 1,2
C) 1,3
D) 1,4
E) 1,5
1.8. Составьте уравнение окружности с центром в начале координат О и радиусом R=7.
A) х2- у2=49
B) у2 - х2 =49
56.
C) х2+у2=49D) х2+у2=7
E) х2- у2=7
Задания уровня В
2.1. Периметр прямоугольника равен 26см, а площадь равна 36см2. Найдите длины сторон
прямоугольника.
[3]
2
2.2. Площадь треугольника равна 40см . Высота в 5 раз меньше стороны, на которую она
опущена. Найти высоту треугольника.
[4]
2.3. Боковая сторона равнобедренного треугольника равна 10 см, а высота, проведенная к
основанию равна 5√3 см. Найдите углы треугольника
[5]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Чему равна сумма внешних углов многоугольника?
A) 1800
B) 3600
C) 4500
D) 5400
E) 6300
1.2. Периметр квадрата равен 3,2 см. Найдите его сторону
A) 0,6
B) 0,65
C) 0,7
D) 0,75
E) 0,8
1.3. Прямая CD параллельна к AB и пересекает угол BOA так, что O,B,D лежат на одной
прямой, а также O,A,C лежат на одной прямой. Если AB=10, OB=6 и OD=24, найдите
длину CD.
A) 30
B) 20
C) 10
D) 15
E) 25
1.4. Тупой угол прямоугольной трапеции равен 1200. Определить ее среднюю линию,
если меньшая диагональ трапеции и большая боковая сторона равны 2.
A) 1,2
B) 1,3
C) 1,4
D) 1,5
E) 1,6
1.5. Дан треугольник, стороны которого 5 см, 3 см, 4 см. Найти периметр треугольника,
вершинами которого являются середины сторон данного треугольника.
A) 8
B) 7
57.
C) 6D) 5
E) 6
1.6. Основания трапеции относятся как 7:3, и разнятся на 3,2 м. Найти сторону средней
линии трапеции.
A) 2
B) 3
C) 4
D) 5
E) 6
1.7. Высота равностороннего треугольника 8,4 см. Найдите расстояние от точки
пересечения биссектрисс треугольника до его стороны.
A) 2,1
B) 2,2
C) 2,3
D) 2,4
E) 2,5
1.8. Составьте уравнение окружности с центром в начале координат О и радиусом R=9.
A) х2- у2=81
B) у2 - х2 =81
C) х2+у2=81
D) х2+у2=9
E) х2- у2=9
Задания уровня В
2
2.1. Площадь ромба 216 см , а длины его диагоналей относятся, как 3:4. Найдите длину
стороны ромба.
[3]
2.2. Большее основание равнобедренной трапеции равно 22м, боковая сторона 8,5м, а
диагональ 19,5м. Найдите площадь трапеции.
[4]
2.3. В прямоугольном треугольнике гипотенуза равна 4√2 см, а один из катетов равен 4 см.
найдите второй катет и острые углы треугольника.
[5]
Критерий оценивания
Находит сумму внутренних
или внешних углов
многоугольника
Находит неизвестную сторону
или неизвестный периметр
четырехугольников
Составляет пропорцию для
сторон подобных
треугольников
Точно определяет вид трапеции
и выполняет черчеж по
№
задания
1.1
1.2
1.3
1.4
Дескриптор
Балл
Применяет теорему о сумме внутренних 1
углов многоугольника. Для нахождения
суммы внешних углов многоугольника
использует следствие из теоремы о
сумме внутренних углов многоугольника
Применяет свойства и признаки
1
четырехугольников для нахождении
неизвестной величины
Применяет теорему Фалеса и находит
1
неизвестную величину
Использует определение, свойства
трапеции, а также теорему о средней
1
58.
условию задачиРешает задачу на нахождение
периметра треугольника с
использованием теоремы о
средней линии треугольника
Составляет уравнение по
условию задачи
1.5
Составляет соотношение для
стороны и медианы
треугольника
Составляет уравнение для
окружности с известным
радиусом
С помощью уравнения решает
задачи на площади
четырехугольников
1.7
Решает задачи на нахождение
площади треугольника /
трапеции
Решает задачи на теорему
Пифагора
Итого
1.6
1.8
2.1
2.2
2.3
линии трапеции, находит соотношение
оснований /среднюю линию трапеций
Применяет теорему о средней линии
треугольника и находит периметр
треугольника
1
Применяет теорему о средней линии
трапеции, составляет уравнение и
решает его
Применяет свойство медиан, высот и
биссектрис треугольника
1
Применяет формулу для уравнения
окружности с центром в точке (0; 0) и
радиусом R
Записывает формулу площади
четырехугольника
Составляет уравнение или систему
уравнений
Решает уравнение и находит
неизвестную величину
Кратко записывает условие задачи
Выполняет черчеж
Применяет формулу площади
треугольника/трапеции
Записывает ответ
Кратко записывает условие задачи
Выполняет черчеж
Применяет теорему Пифагора
Находит длину второго катета
Применяет определение синуса,
косинуса или тангенса угла
треугольника и находит углы
треугольника.
1
1
1
1
1
1
1
1
1
1
1
1
1
20
Комплексная диагностическая работа
по алгебре и началам анализа 10 класс 2021-2022 учебный год
авторы: Маркель Татьяна Петровна, Северо-Казахстанская область, район
М.Жумабаева, КГУ «Таманский комплекс школа-ясли-сад», педагог-эксперт
Жуменко Светлана Николаевна, Алматинская обл., г.Талдыкорган, КГУСШГ 16,
учитель высшей категории
Продолжительность – 45 минут
Типы заданий:
МВО
–
задания
с
множественным
выбором
ответов;
РО – задания, требующие развернутого ответа
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Решение систем нелинейных
1.1
МВО
9.2.2.2 решать системы нелинейных
59.
уравнений с двумяпеременными.
Арифметическая прогрессия
уравнений с двумя переменными.
1.2
МВО
9.2.3.5 знать и применять формулы
n-го члена, суммы n первых членов и
характеристическое свойство
арифметической прогрессии.
9.2.4.2 знать взаимосвязь координат
точек (cos ; sin ) единичной
окружности с тригонометрическими
функциями
9.2.4.6 объяснять с помощью
единичной окружности чётность
(нечётность), периодичность,
монотонность и промежутки
знакопостоянства.
9.2.2.4 решать системы нелинейных
неравенств с двумя переменными
Значения синуса, косинуса,
тангенса и котангенса
углов.
1.3
МВО
Тригонометрические
функции и их свойства.
1.4
МВО
Системы нелинейных
неравенств с двумя
переменными.
Основные
тригонометрические
тождества
Сумма членов бесконечно
убывающей геометрической
прогрессии.
1.5
МВО
1.6
МВО
1.7
МВО
Формулы тригонометрии.
1.8
МВО
Решение текстовых задач с
помощью
систем нелинейных
уравнений
с двумя переменными.
Тождественные
преобразования
тригонометрических
выражений.
Геометрическая прогрессия
2.1
РО
2.2
РО
9.2.4.8 выполнять тождественные
преобразования тригонометрических
выражений
2.3
РО
9.2.3.6 знать и применять формулы
n-го члена, суммы n первых членов и
характеристическое свойство
геометрической прогрессии
9.2.4.8 выполнять тождественные
преобразования тригонометрических
выражений
9.2.3.8 применять формулу суммы
бесконечно убывающей
геометрической прогрессии для
перевода десятичной периодической
дроби в обыкновенную дробь
9.2.4.4 выводить и применять
формулы приведения
9.4.2.1 решать текстовые задачи с
помощью систем уравнений
Вариант 1
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.3.
х 2 ху 36
Решите систему уравнений
ху у 2 45
A) (4;-5); (-4;5)
B) (-4;-5); (-4;5)
C) (4;5); (-4;5)
60.
D) (4;5); (-4;-5)1.2. Второй член арифметической прогрессии равен 9, а ее третий член больше первого
на 12. Найдите сумму десяти первых членов прогрессии.
A) 280
B) 300
C) 320
D) 310
1.3. Найдите числовое значение выражения: 3 sin 2 cos ctg 2
6
6
A) 2
B) 3,5
C) 2,5
D) 3
1.4. Найдите наименьший положительный период функции y sin 2 x cos 2 x
A)
B)
2
C) 2
D) 4
x 2 y 2 16
1.5. На каком из рисунков изображено решение системы неравенств
x 1,5
A)
C)
B)
D)
5
1.6. Вычислите tg , если sin ; .
13 2
5
A)
12
5
B)
12
61.
125
12
D)
5
1.7. Представьте бесконечную периодическую дробь 1,2(6) в виде обыкновенной дроби.
1
A) 1
15
2
B) 1
15
1
C) 1
5
4
D) 1
15
C)
1.8. Упростите выражение 1 cos sin
2
A) 0
B) cos 2
C) - 1
D) sin 2
Задания уровня В
2.1. Двое рабочих могут закончить определенную работу за 12 дней. После 8-дневной
совместной работы один из ни заболел. Второй рабочий закончил оставшуюся работу за 5
дней. Сколько дней понадобится каждому работнику, чтобы выполнить работу по
отдельности?
sin 3 sin
2.2. Докажите тождество
tg 2
cos 3 cos
2.3. Определите число членов геометрической прогрессии, если известно, что, если
b3 b1 8, b6 b4 216 , S n 121
Вариант 2
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
2
х ху 6
1.4. Решите систему уравнений
2
ху у 10
A) (1,5;- 2,5); (-1,5;5,5)
B) (- 1,5;2,5); (-1,5;5,5)
C) (1,5;2,5); (-1,5;5,5)
D) (1,5;2,5); (1,5; - 5,5)
1.2. Сумма первого и третьего членов арифметической прогрессии равна 12,
а ее
четвертый член равен 12 . Найдите сумму первых пятнадцати членов прогрессии.
A) 350
62.
B) 300C) 320
D) 360
1.3. Найдите числовое значение выражения: 3tg
4
sin 2
3
cos 2
6
A) 2
B) 3,5
C) 2,5
D) 3
x
1.4. Найдите наименьший положительный период функции y 2tg
3 4
A)
B)
2
C) 3
D) 4
x 2 y 2 36
1.5. На каком из рисунков изображено решение системы неравенств
x 1,5
1.6. Вычислите tg , если cos
8
15
8
B)
15
15
C)
8
15
D)
8
A)
15
; .
17 2
63.
1.7. Представьте бесконечную периодическую дробь 10,5(3) в виде обыкновенной дроби.1
A) 10
3
8
B) 10
15
2
C) 10
5
7
D) 10
15
cos tg
1.8. Упростите выражение
sin
2
A) 0
B) tg
C) - 1
D) tg
Задания уровня В
3
всей работы. Они
4
закончили работу за 10 дней, хотя второй рабочий не вышел на работу последние 2 дня. За
сколько дней закончит работу каждый рабочий в отдельности?
2.1. Двое рабочих, совместно проработав 7 дней, выполнили
sin 72 0 sin 180
1
cos 72 0 cos18 0
2.3. Определите число членов геометрической прогрессии, если известно, что, если
b4 b1 23, b6 b5 368, S n 23
2.2. Докажите тождество
Критерий оценивания
решает системы нелинейных
уравнений с двумя переменными
применяет формулы n-го члена,
суммы n первых членов
арифметической прогрессии
Находит числовое значение
выражения
№
задания
1.1
1.2
1.3
Определяет периодичность
тригонометрической функции
1.4
Выбирает из изображенных
рисунков решение системы
неравенств.
Применяет основные
тригонометрические тождества
при нахождении значения
1.5
1.6
Дескриптор
Балл
Решает систему уравнений способом
сложения
Использует формулу нахождения
суммы первых членов
арифметической прогрессии
Использует значения
тригонометрических функций и
находит значение выражения
Использует основной период
функций для нахождения
наименьшего положительного
периода заданной функции
Решает системы нелинейных
неравенств с двумя переменными
1
Использует свойства функций и
основные тригонометрические
тождества.
1
1
1
1
1
64.
тригонометрической функцииприменяет формулу суммы
бесконечно убывающей
геометрической прогрессии для
перевода десятичной
периодической дроби в
обыкновенную дробь
Упрощает тригонометрическое
выражение
решает текстовые задачи с
помощью систем уравнений
Доказывает тригонометрическое
тождество
Определяет число членов
геометрической прогрессии
1.7
Переводит десятичную
периодическую дробь в
обыкновенную дробь
1
1.8
Упрощает выражение используя
формулы приведения
Вводит переменные
Находит часть работы выполненные
рабочими отдельно
Составляет систему уравнений
Находит сколько дней работал 1
рабочий
Находит сколько дней работал 1
рабочий
Использует формулу синус суммы
(разности) двух углов
Использует формулу косинус суммы
(разности) двух углов
Сокращает дробь
1
2.1
2.2
2.3
Использует основное
тригонометрическое тождество
Составляет систему уравнений
Находит знаменатель
Находит первый член прогрессии
находит число членов
геометрической прогрессии
Итого
1
1
1
1
1
1
1
1
1
1
1
1
1
19
Комплексная диагностическая работа
по геометрии 10 класс 2021-2022 учебный год
Авторы: Романович Юлия Ивановна, Костанайская область, Коммунальное
государственное учреждение "Гимназия отдела образования Житикаринского района"
Управления образования акимата Костанайской области, педагог-исследователь
Продолжительность – 45 минут
Типы заданий:
МВО
–
задания
с
множественным
выбором
ответов;
РО – задания, требующие развернутого ответа
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Координаты вектора.
1.1
МВО
9.1.3.1 находить координаты вектора;
Угол между векторами.
Скалярное
произаедение векторов
Сложение векторов
1.2
МВО
9.1.4.6 находить
векторов;
скалярное
произведение
1.3
МВО
9.1.4.2 знать и применять правила сложения
векторов ;
65.
Координаты вектораОсевая симметрия
1.4
1.5
МВО
МВО
Признаки подобия
треугольников.
Углы, вписанные в
окружность
Площадь круга и его
частей
Теорема синусов и
косинусов
1.6
МВО
1.7
МВО
1.8
МВО
2.1
РО
Подобие фигур.
Гомотетия.
2.2
РО
Правильные
многоугольники и
окружность
2.3
РО
9.1.3.2 находить длину вектора;
9.1.4.9 строить образы фигур при симметриях,
параллельном переносе, повороте;
9.1.4.15 знать и применять подобие
прямоугольных треугольников
9.1.1.3 знать определение вписанного угла и его
свойства;
9.1.1.2 выводить и применять формулу
площади сектора, сегмента;
9.1.3.10 применять теоремы синусов и
косинусов для решения треугольников и
прикладных задач;
9.1.4.17 знать формулу зависимости между
площадями подобных фигур и коэффициентом
подобия;
9.1.2.5 знать и применять формулы,
связывающие стороны, периметр, площадь
правильного многоугольника и радиусы
вписанной и описанной окружностей
правильного многоугольника;
I вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1 Определите координаты вектора
: если А(2;-1) и В(-4;2)
A)
B)
C)
D)
E)
1.2 Найти скалярное произведение векторов: а (0; 3 ) и в (2;
A) 5
B) 3
C) 6
D)
3)
E)
Упростите выражение: (
1.3
+(
)
A)
B)
C)
D)
)
66.
E)1.4 Найти длину вектора
(7; 5 )
A) 54
B) 74
C)
D)
E)
1.5 Сколько осей симметрии имеет правильный шестиугольник
A) 5
B) 3
C) 6
D) 4
E) 2
1.6 В прямоугольном треугольники АВС ( С=900). Найдите высоту СН, если АН =3 см,
ВН=6 см
A)
B)
C)
D)
E)
1.7 Найдите вписанный угол, опирающийся на дугу, которая составит 2/5 окружности.
A) 540
B) 660
C) 600
D) 720
E) 1440
1.8 Найти площадь сектора круга радиусом 2, если соответствующий этому сектору
центральный угол равен 600
2
A)
3
B)
3
C)
6
3
D)
4
E)
15
Задания уровня В
2.1 В треугольнике АВС АС=12см, А=750, С=600. Найдите АВ и площадь
треугольника
67.
[6]2.2 Найдите коэффициент подобия двух квадратов, если периметр первого равна 24см, а
сторона второго квадрата 18см.
[2]
2.3 Квадрат со стороной 6 2 вписан в окружность. Найдите сторону
треугольника описанного около этой окружности.
правильного
[3]
II вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1 Определите координаты вектора
: если А(-1;3) и В(4;2)
A)
B)
C)
D)
E)
1.2 Найти скалярное произведение векторов: а (5; 5 ) и в (2;0)
A) 5
B) 10
C) 25
D)
E)
Упростите выражение:
1.3
A)
B)
C)
D)
E)
1.4 Найти длину вектора а (-6;
)
A) 39
B) 47
C)
D)
E)
1.5 Сколько осей симметрии имеет ромб
A) 0
B) 3
C) 1
D) 4
68.
E) 21.6 В прямоугольном треугольники АВС ( С=900). Найдите высоту СН, если АН =3 см,
ВН=9 см
A)
B)
C)
D)
E)
1.7 Найдите вписанный угол, опирающийся на дугу, которая составит 7/12 окружности.
A) 1540
B) 1000
C) 1600
D) 2100
E) 1050
1.8 Найти площадь сектора круга радиусом 2, если соответствующий этому сектору
центральный угол равен 600
A) 3
B)
C)
6
D) 2
E)
15
Задания уровня В
2.1 В треугольнике АВС АС=10см, А=750, С=450. Найдите АВ и площадь
треугольника
[6]
2.2 Найдите коэффициент подобия двух квадратов, если периметр первого равна 36см, а
сторона второго квадрата 18см.
[2]
2.3 Квадрат со стороной 4 2 вписан в окружность. Найдите сторону правильного
треугольника описанного около этой окружности.
[3]
Критерий оценивания
Находит координаты вектора
Находит скалярное произведение векторов
Выполняет преобразование, применяет
Вариант 1
№
Дескриптор
задания
1.1
D
1.2
B
1.3
B
Балл
1
1
1
69.
правила сложения векторовНаходит длину вектора
Строит образы фигур при симметриях,
параллельном переносе, повороте
Применяет подобие прямоугольных
треугольников при решении задач
Находит вписанный угол, опирающийся на
дугу, применяет определение вписанного
угла и его свойства
Применяет формулу площади сектора,
сегмента при решении задач
Применяет теоремы синусов и косинусов
для решения треугольников и прикладных
задач
Знает и применяет формулу зависимости
между площадями подобных фигур и
коэффициентом подобия
Знает и применяет формулы, связывающие
стороны, периметр, площадь правильного
многоугольника и радиусы вписанной и
описанной окружностей правильного
многоугольника
1.4
1.5
D
С
1
1
1.6
А
1
1.7
D
1
1.8
А
1
2.1
использует свойство суммы углов
треугольника
находит угол В
использует теорему синусов
вычисляет сторону АВ
использует формулу площади
треугольника
вычисляет площадь треугольника
применяет формулу зависимости
между площадями подобных
фигур и коэффициентом подобия
вычисляет коэффициент подобия
1
использует формулу a4=
вычисляет радиус описанной
окружности
использует формулу
и
1
2.2
2.3
Находит координаты вектора
Находит скалярное произведение векторов
Выполняет преобразование, применяет
правила сложения векторов
Находит длину вектора
Строит образы фигур при симметриях,
параллельном переносе, повороте
Применяет подобие прямоугольных
треугольников при решении задач
Находит вписанный угол, опирающийся на
дугу, применяет определение вписанного
угла и его свойства
Применяет формулу площади сектора,
сегмента при решении задач
Применяет теоремы синусов и косинусов
для решения треугольников и прикладных
1
1
1
1
1
вычисляет сторону треугольника
Итого
Критерий оценивания
1
1
1
1
19
Вариант 2
№
Дескриптор
задания
1.1
D
1.2
B
1.3
C
Балл
1
1
1
1.4
1.5
C
E
1
1
1.6
B
1
1.7
E
1
1.8
А
1
2.1
использует свойство суммы углов
треугольника
1
70.
задачЗнает и применяет формулу зависимости
между площадями подобных фигур и
коэффициентом подобия
Знает и применяет формулы, связывающие
стороны, периметр, площадь правильного
многоугольника и радиусы вписанной и
описанной окружностей правильного
многоугольника
Итого
2.2
2.3
находит угол В
использует теорему синусов
вычисляет сторону АВ
использует формулу площади
треугольника
вычисляет площадь треугольника
применяет формулу зависимости
между площадями подобных
фигур и коэффициентом подобия
вычисляет коэффициент подобия
1
1
1
1
использует формулу a4=
вычисляет радиус описанной
окружности
использует формулу
и
1
1
1
1
1
1
вычисляет сторону треугольника
19
Комплексная диагностическая работа
по алгебре 10 класс 2021-2022 учебный год
автор: Арютина Светлана Иосифовна, педагог-эксперт, Северо-Казахстанская
область, КГУ «Заградовская средняя школа» КГУ «Отдел образования Есильского
района» КГУ «Управление образования акимата Северо-Казахстанской области»
Продолжительность – 45 минут
Количество баллов – 10
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задания задания
Нелинейные уравнения с
А1
МВО
9.2.2.2 решать системы нелинейных
двумя переменными и их
уравнений с двумя переменными
системы
Арифметическая
А2
МВО
9.2.3.5 знать и применять формулы п-го
прогрессия
члена, суммы п первых членов и
характеристическое свойство
арифметической прогрессии
Геометрическая
А3
МВО
9.2.3.6 знать и применять формулы ппрогрессия
го члена, суммы п первых членов и
характеристическое свойство
геометрической прогрессии
Формулы тригонометрии
А4
МВО
9.2.4.4 выводить и применять формулы
приведения
Тригонометрические
А5
МВО
9.2.4.6 объяснять с помощью единичной
функции и их свойства
окружности чётность(нечётность),
периодичность, монотонность и
промежутки знакопостоянства
тригонометрических функций
71.
Системы нелинейныхнеравенств с двумя
переменными
Тождественные
преобразования
тригонометрических
выражений
Нелинейные уравнения с
двумя переменными и их
системы
А6
МВО
9.2.2.4 решать системы нелинейных
неравенств с двумя переменными
В1
РО
9.2.4.8 выполнять тождественные
преобразования тригонометрических
выражений
В2
РО
9.4.2.1 решать текстовые задачи с
помощью систем уравнений
1 вариант
Уровень А
А1. Система
имеет:
1) одно решение;
2) четыре решения;
А2. В арифметической прогрессии
1) ;
2)
;
3) 2.
. Разность этой прогрессии равна:
А3. В геометрической прогрессии
равна:
3)
;
2)
;
3)
3) ни одного?
.
Сумма первых её пяти членов
.
А4. Чему равно значение
1)
;
2)
;
4) –cos
3) -sin ;
А5. Выражение
принимает значение:
2) равное нулю;
2) меньше нуля;
3) больше нуля.
А6. На каком рисунке изображено множество решений системы неравенств
х 2 у 2 9,
2 у х 4 0?
1)
2)
3)
4)
Уровень В
В1. Доказать тождество:
[2 балла]
В2. Найдите два натуральных числа, если их среднее арифметическое равно 35, а их
среднее геометрическое равно 28.
[2 балла]
2 вариант
72.
Уровень АА1. Система
имеет:
1) одно решение;
2) четыре решения;
А2. В арифметической прогрессии
равна:
2)
;
2)
;
3) 22,5.
А3. В геометрической прогрессии
равна:
1)
;
2)
;
3)
3) ни одного?
. Разность этой прогрессии
.
Сумма первых её пяти членов
.
А4. Чему равно значение
1)
;
2)
;
3) -sin ;
4) –cos
А5. Выражение
принимает значение:
1) меньше нуля;
2) больше нуля;
3) равное нулю.
А6. На каком рисунке изображено множество решений системы неравенств
х 2 у 2 9,
2 у х 4 0?
1)
2)
3)
4)
Уровень В
В1. Доказать тождество:
[2 балла]
В2. Найдите два натуральных числа, если их среднее арифметическое равно 61, а их
среднее геометрическое равно 60.
[2
балла]
Критерий оценивания
Определяет количество решений
системы нелинейных уравнений с
двумя переменными
Вычисляют разность
арифметической прогрессии,
используя формулу п-го члена
Определяют сумму первых п членов
геометрической прогрессии
№
задания
А1
А2
А3
Дескриптор
Балл
Умеет определять количество
решений систем нелинейных
уравнений с двумя
переменными
Использует формулу
вычисления разности
геометрической прогрессии
Использует формулу
нахождения суммы первых
членов геометрической
1
1
1
73.
Применяют формулу приведенияА4
Используя промежутки
А5
знакопостоянства определяют знак
выражения
Находят решение систем нелинейных А6
неравенств с двумя переменными
Используют тождественные
преобразования тригонометрических
выражений для доказательства
тождеств
В1
В2
Решают текстовые задачи с помощью
систем уравнений
Итого:
прогрессии
Использует формулы
приведения
Использует промежутки
знакопостоянства
Решает системы нелинейных
неравенств с двумя
переменными
Использует формулы
тригонометрии для упрощения
выражения
Выполняет тождественные
преобразования
Вводит переменные и по
условию задачи составляет
систему уравнений
Решает систему уравнений
1
1
1
1
1
1
1
10
Диагностическая контрольная работа
по геометрии 10 класс 2021-2022 учебный год
автор: Арютина Светлана Иосифовна, педагог-эксперт, Северо-Казахстанская
область, КГУ «Заградовская средняя школа» КГУ «Отдел образования Есильского
района» КГУ «Управление образования акимата Северо-Казахстанской области»
Продолжительность – 45 минут
Количество баллов – 10
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
№
Тип
Проверяемая цель
задания задания
Вектор. Коллинеарные
А1
МВО
9.1.4.1 знать определение вектора,
и неколлинеарные
коллинеарных векторов, равных векторов,
векторы
нулевого вектора, единичного вектора и
длины вектора
Действия над
А2
МВО
9.1.3.3 выполнять действия над векторами,
векторами.
записанными в координатах
Координаты вектора
А3
МВО
9.1.3.2 находить длину вектора
Угол между
А4
МВО
9.1.4.5 знать определение угла между
векторами. Скалярное
двумя векторами
произведение
векторов.
Осевая симметрия
А5
МВО
9.1.4.9 строить образы фигур при
симметриях, параллельном переносе,
повороте
Подобие фигур.
А6
МВО
9.1.4.13 знать определение и свойство
гомотетия
подобных фигур
Решение
В1
РО
9.1.3.6 знать и применять теорему
треугольников
косинусов
74.
Правильныемногоугольники
В2
РО
9.1.2.5 знать и применять формулы,
связывающие стороны, периметр, площадь
правильного многоугольника и радиусы
вписанной и описанной окружностей
правильного многоугольника
1 вариант
Уровень А
А1. По координатам точек А (10; 5), В (– 9; 9) и С(-17; 11) определите каковы эти
векторы
. Выберите правильный ответ:
1) коллинеарны;
2) равные;
3) сонаправленные;
4) равной
длины.
А2. Найдите координаты вектора
, если
,
1) (3;2); 2) (-3;-2);
3) (-3;2);
4) (3;-2)
А3. Найдите длину вектора p(-4;5)
1) -36;
2) -6;
3) 6;
4) 36
А4. Если скалярное произведение векторов равно нулю, то угол между векторами:
1) тупой;
2) развернутый;
3) острый;
4) прямой.
А5. Сколько осей симметрии имеет равносторонний треугольник?
1) Одну
2) Две
3) Три
4) Не имеет осей симметрии
А6. Периметр одного из 2х подобных треугольников равен 48 см, а коэффициент подобия
этих треугольников равен 2. Чему может быть равен периметр второго треугольника?
1) 96 см;
2) 24 см;
3) 50 см;
4) 46 см.
Уровень В
В1. Две стороны треугольника равны 6 см и 16 см, а угол между ними . Найдите
периметр и площадь треугольника.
[2 балла]
2
В2. Площадь круга, описанного около квадрата АВСД, равна 8π (пи) см (в квадрате).
Найдите сторону и площадь треугольника ДАВ.
[2
балла]
2 вариант
Уровень А
А1. По координатам точек А (12; 1), В (13; 0), С(1; 8) и Д(2;7) определите каковы эти
векторы
. Выберите правильный ответ:
1) коллинеарны;
2) равные;
3) сонаправленные;
4) равной
длины.
А2. Найдите координаты вектора
, если
,
1) (-3;6); 2) (-3;-6);
3) (3;-6);
4) (3;6)
А3. Найдите длину вектора p(3;-4)
1) 25;
2) 5;
3) -5;
4) -25
А4. Чему равен угол между противоположно направленными векторами:
1) нулю;
2) 90 градусов;
3) 180 градусов;
4) любому положительному
числу
А5. Сколько осей симметрии имеет разносторонний треугольник?
1) Одну 2) Две 3) Три 4) Не имеет осей симметрии
А6. Периметр одного из 2х подобных треугольников равен 26 см, а коэффициент подобия
этих треугольников равен 2. Чему может быть равен периметр второго треугольника?
2) 52 см;
2) 13 см;
3) 28 см;
4) 24 см.
75.
Уровень ВВ1. Две стороны треугольника равны 6 см и 10 см, а угол между ними . Найдите
периметр и площадь треугольника.
[2
балла]
В2. Площадь круга, описанного около квадрата АВСД, равна 12π (пи) см2 (в квадрате).
Найдите сторону и площадь треугольника ДАВ.
[2
балла]
Критерий оценивания
№ задания Дескриптор
Балл
Определяет вид вектора
А1
Называет вид вектора
1
Определяет разность векторов,
А2
Находит разность векторов
1
записанных в координатах
Вычисляет длину вектора
А3
Вычисляет длину вектора
1
Определяет угол между двумя
А4
Указывает вид угла
1
векторами
Определяет осевую симметрию
А5
Называет количество осей
1
симметрии
Использует свойство подобных
А6
Вычисляет периметр
1
фигур
подобного треугольника
В1
Записывает теорему косинусов 1
и вычисляет длину третьей
Применяет теорему косинусов
стороны
Находит периметр и площадь
1
треугольника
Применяет формулы, связывающие В2
Вычисляет радиус круга и
1
стороны, периметр, площадь
использует его для нахождения
правильного многоугольника и
стороны квадрата
радиусы вписанной и описанной
Вычисляет площадь
1
окружностей правильного
треугольника
многоугольника
Итого:
10
Комплексная диагностическая работа
по алгебре и началам анализа 11 класс 2021-2022 учебный год
Авторы: Середкин В.П. учитель математики, педагог-мастер, Павлодарская область,
Павлодарский район, КГУ Чернорецкая СОШ № 1.,
Подгорнова О.В. учитель математики, педагог-исследователь, ВКО, Шемонаихинский
район, КГУ «Убинская общеобразовательная средняя школа» отдела образования по
Шемонаихинскому району управления образования ВКО
Продолжительность – 45 минут
Типы заданий:
МВО
–
задания
с
множественным
выбором
ответов;
РО – задания, требующие развернутого ответа
Характеристика заданий
ТЕМА
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
Функции и ее графики
1.1
МВО
10.4.1.7 - уметь распознавать
сложную функцию f(g(x)) и
составлять композицию функций;
76.
Тригонометрическиефункции
1.2
МВО
Обратные
тригонометрические
функции
Тригонометрические
уравнения
Вероятность
1.3
МВО
1.4
МВО
1.5
МВО
Предел функции и
непрерывность
Производная
1.6
МВО
1.7
МВО
Случайные величины и их
числовые характеристики
1.8
МВО
Применение производной
2.1
РО
Тригонометрические
неравенства
Многочлены
2.2
РО
2.3
РО
10.2.3.1 - знать определения, свойства
тригонометрических функций и уметь
строить их графики;
10.2.3.6 - выполнять преобразования
выражений, содержащих обратные
тригонометрические функции;
10.2.3.8 Уметь решать простейшие
тригонометрические уравнения
10.3.1.4 Решать задачи на нахождение
вероятностей, применяя формулы
комбинаторики
10.4.1.8 Знать определение предела
функции в точке и вычислять его
10.4.1.25 Составлять уравнение
касательной к графику функции в
заданной точке
10.3.2.13 Вычислять математическое
ожидание дискретной случайной
величины
10.4.1.33 Исследовать свойства
функции с помощью производной и
строить её график
10.2.3.18 Уметь решать
тригонометрические неравенства
10.2.1.5 Находить корни многочлена с
одной переменной методом
разложения его на множители
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Даны функции f ( x) 2 x 3 и g ( x) x 2 5 . Найдите g ( f ( x))
A) 4x 2 12x 14
B) 4 x 2 12x 5
C) 4 x 2 12x 4 +
D) 4 x 2 12x 4
E) 4 x 2 12x 5
1.2. График, какой функции изображен на рисунке?
A) y sin 2 x
B) y sin x +
1
C) y sin x
2
D) y 2 sin x
77.
E) y1
sin x
2
1.3. Вычислите: arctg 3 arcctg ( 1) arctg (
7
12
5
B)
12
5
C)
12
7
D)
12
9
E)
12
3
)
3
A)
1.4. Решите уравнение 2 cos x
A) 1 n
B)
C)
4
D)
4
4
4
8
2
n, n Z
n, n Z
n
2
,n Z
2 n, n Z
2 n, n Z
4
1.5. В корзине 6 яблок и 5 апельсинов. Наугад выбирают три фрукта. Какова вероятность,
что все три фрукта – яблоки.
4
A)
33
6
B)
33
5
C)
33
11
D)
33
1
E)
33
E)
1.6. Вычислите
lim
x 3
4
27
1
B)
27
A)
x 2 5x 6
3x 2 9 x
78.
527
11
D)
27
6
E)
27
1.7. Укажите уравнение касательной к графику функции, f ( x) 2 x 2 1 проходящую
C)
через точку x0 1
A) y 4 x
B) y 4 x 3
C) y 4 x 3
D) y 4 x
E) y 4 x 3
1.8. Найти математическое ожидание дискретной случайной величины X, заданной
законом распределения
x
1
4
7
12
p
0,08
0,35
0,22
0,35
A)1
B) 7,22
C) 7,2
D) 72,2
E) 6,22
Задания уровня В
5
3
2.1. Исследуйте функцию y x 3 x 2 2 x и постройте ее график
2
2
2.2. Решите неравенство cos 3 x 1
2
2
3
2
2.3 Решите уравнение x x 4x 2 0
[5]
[3]
[3]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1.Даны функции f ( x) 3x 2 и g ( x) x 2 1 . Найдите g ( f ( x))
A) 9x 2 12x 3
B) 9 x 2 12x 5
C) 9 x 2 12x 6
D) 9x 2 12x 3
E) 9x 2 12x 5
1.2. График, какой функции изображен на рисунке?
79.
A) y cos 2 xB) y cos x
1
C) y cos x
2
D) y 2 cos x
1
E) y cos x
2
1.3. Вычислите: arcctg 3 arcctg ( 1) arcctg (
21
12
5
B)
12
3
)
3
A)
C)
D)
12
4
17
E)
12
1.4. Решите уравнение 2 sin x
A) 1 n
B) 1 n
C) 1 n
D) 1 n
E) 1 n
3
6
3
6
12
2
n, n Z
n, n Z
2 n, n Z
2 n, n Z
n, n Z
4
1.5. В ящике 6 яблок и 9 груш. Наудачу извлекают три фрукта. Какова вероятность того,
что все три фрукта – яблоки.
4
A)
91
6
B)
91
5
C)
91
11
D)
91
80.
E)1
91
1.6. Вычислите
lim
x 2
x 2 3x 2
2x2 4x
3
4
1
B)
4
5
C)
4
1
D)
2
7
E)
4
1.7. Укажите уравнение касательной к графику функции f ( x) 3x 2 2 проходящую
A)
через точку x0 1
A) y 6 x
B) y 6 x 5
C) y 6 x 7
D) y 6 x
E) y 6 x 5
1.8. Найти математическое ожидание дискретной случайной величины X, заданной
законом распределения
x
2
3
9
11
p
0,01
0,09
0,25
0,65
A)1
B) 6,96
C) 9,6
D) 96,9
E) 9,69
Задания уровня В
х
х
2 х 3 и постройте ее график
3
2
3
2.1. Исследуйте функцию f(x)=
2
3
2.2. Решите неравенство sin 2 x
4 2
3
2
2.3 Решите уравнение x x 4x 6 0
Критерий оценивания
Составляет композицию функций
№
задания
1.1
[5]
[3]
[3]
Дескриптор
Балл
Подставляет выражение вместо
аргумента и составляет сложную
функцию
1
81.
Устанавливает соответствиемежду формулой и графиком
функции
Выполняет преобразование
выражений, содержащих
обратные тригонометрические
функции
Решает простейшие
тригонометрические уравнения
1.2
Указывает функцию, график которой
изображен на рисунке
1
1.3
Выполняет преобразования и
находит значение выражения
1
1.4
1
Решает задачу на нахождение
вероятности
1.5
Вычисляет предел функции в
точке
Составляет уравнение
касательной к графику функции в
заданной точке
Вычисляет математическое
ожидание дискретной случайной
величины
Исследует свойства функции с
помощью производной и строит
график на основе ее
исследования
1.6
Использует формулу нахождения
корней простейшего уравнения для
косинуса/синуса и находит решение
уравнения
Применяет правило умножения
вероятностей для независимых
событий
Выполняет преобразования и
вычисляет значение предела
Составляет уравнение касательной
1.8
Вычисляет значение
математического ожидания
1
2.1
Находит область определения,
исследует на четность/ нечетность и
периодичность
Находит нули функции и
промежутки знакопостоянства,
исследует функцию на
непрерывность и наличие асимптот
Находит интервалы монотонности,
экстремумы функции
Находит точки перегиба, интервалы
выпуклости графика
Строит график функции
Вводит новую переменную, заменяя
аргумент
Изображает решение на
тригонометрическом круге
Определяет множество решений
неравенства, записывает ответ
Выбирает метод для разложения
многочлена на множители
Раскладывает многочлен на простые
множители
Находит корни многочлена
1
Решает тригонометрические
неравенства
Находит корни многочлена с
одной переменной
1.7
2.2
2.3
Итого
Комплексная диагностическая работа
по геометрии 11 класс 2021-2022 учебный год
1
1
1
1
1
1
1
1
1
1
1
1
1
19
82.
автор: Фазылова Татьяна Михайловна Государственное коммунальное учреждение"Средняя школа №1 имени Жамбыла" государственного учреждения "Отдел образования
по Балхашскому району Управления образования Алматинской области",
Высшая
категория
Продолжительность – 45 минут
Типы заданий:
МВО
–
задания
с
множественным
выбором
ответов;
РО – задания, требующие развернутого ответа
ТЕМА
Аксиомы стереометрии
Параллельность в
пространстве
Параллельность
плоскостей
Перпендикулярность в
пространстве
Теорема о трех
перпендикулярах
Расстояние между
точками
Прямоугольная система
координат и векторы в
пространстве
Прямоугольная система
координат и векторы в
пространстве
Прямоугольная система
координат и векторы в
пространстве
Характеристика заданий
№
Тип
ПРОВЕРЯЕМАЯ ЦЕЛЬ
задания задания
1.1
МВО
10.2.3 Знать свойства параллельных
прямых в пространстве и применять их
при решении задач
1.2
МВО
10.2.4 Знать признак и свойства
параллельности прямой и плоскости,
применять их при решении задач
1.3
МВО
10.2.5 Знать признак и свойства
параллельности плоскостей, применять
их при решении задач
1.4
МВО
10.2.8 - знать определение
перпендикуляра, наклонной и проекции
наклонной в пространстве
1.5
МВО
10.3.1 - знать теорему о трех
перпендикулярах и применять её при
решении задач;
1.6
МВО
10.3.5 - уметь находить расстояние от
точки до плоскости и между
скрещивающимися прямыми;
1.7
МВО
10.4.2 Выполнять сложение векторов и
умножение вектора на число
1.8
МВО
10.4.3 Знать определение коллинеарных
и компланарных векторов в пространстве
2.1
РО
Скалярное произведение
векторов
2.2
РО
10.3.6 Знать формулу площади
ортогональной проекции плоской
фигуры на плоскость и применять ее при
решении задач
10.4.17 Вычислять угол между
двумя векторами в пространстве
Уравнение плоскости в
пространстве
2.3
РО
10.4.10 Знать уравнение сферы и
применять его при решении задач
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Сколько плоскостей можно провести через три точки пространства не
принадлежащие одной прямой.
83.
A) Ни однойB) Три
C) Одну
D) Бесконечно много
1.2.
Для правильной шестиугольной призмы АBCDEFA1B1C1D1E1F1
укажите ребро параллельное ребру B1C1
A)AA1
B) C1D1
C) EF
D) DE
1.3.
Назовите общую прямую плоскостей РВМ и МАВ
A) РМ;
B) А В;
C) РВ;
D) ВМ.
1.4. Точка А отстоит от плоскости на расстоянии 18см. Найдите длину наклонной,
проведенной из нее под углом 600 к этой плоскости.
A)
B)
C)
D) 8
9
12
1.5. . Из точки В — вершины прямоугольника АВСD восстановлен перпендикуляр ВМ к
плоскости прямоугольника. Найти МD, если CD=8, МС=15.
A)17 см
B) 12 см
C) 13 см
D) 20 см
E)
1.6. Расстояние от точки D до каждой из вершин равностороннего треугольника АВС
равно 4 см. АВ=6 см. Найдите расстояние от точки М до плоскости АВС.
A)2 см
B) 4 см
C) 3 см
D) 6 см
1.7.
Даны векторы
A)
B)
C)
D)
1.8. Дан куб АВСDА1В1С1D1
и
. Найти координаты вектора
84.
Найдите, какие из трех векторов будут компланарныА)
друг другу
В)
С)
Задания уровня В
2.1. Ребро куба ABCDA1B1C1D1 равно 4 см. Через диагональ основания BD под углом
45° к плоскости основания проведена плоскость BDK, пересекающая боковое ребро
в точке K. Найдите площадь треугольника BDK.
[2]
2.2. Найдите угол между вектором (5; -1; 7) и осью ОХ
[3]
2.3. Напишите уравнение сферы с центром в начале координат,
если плоскость х=5 касается этой сферы.
Сфера задана уравнением х2 + y2 + z2 -2x + 4y - 6z - 2=0 .
Найдите координаты центра сферы и ее радиус.
[3]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
1.1. Сколько плоскостей можно провести через три точки пространства принадлежащие
одной прямой.
A)Ни одной
B)Три
C)Одну
D)Бесконечно много
1.2. Для правильной шестиугольной пирамиды SАBCDEF укажите прямую,
параллельную линии пересечения плоскостей SАB и SDE:
A)BC
B) CF
C) AD
D) BE
1.3 Назовите общую прямую плоскостей AFD и DEF.
А) AF;
В) FD;
C) AE;
D) ) ED.
85.
1.4. Точка А отстоит от плоскости на расстоянии 12см. Найдите длинунаклонной, проведенной из нее под углом 600 к этой плоскости.
A) 8
B) 4
C) 2
D) 6
1.5. Из точки вне плоскости проведены к ней две наклонные, одна из которых
равна 16 см и наклонена под углом 30° к плоскости. Определить длину
второй наклонной, если ее проекция на плоскость равна 15 см.
A)12 см
B) 13см
C) 10 см
D) 17 см
1.6. Расстояние от точки D до каждой из вершин равностороннего треугольника АВС
равно 5 см. АВ=3 см. Найдите расстояние от точки М до плоскости АВС
A) 4 см
B) 3 см
C) 5 см
D) 2 см
1.7 Даны векторы
Найти координаты вектора
.
.
A)
B)
C)
D)
1.8.
Дан куб АВСDА1В1С1D1
Найдите, какие из трех векторов будут компланарны
А)
друг другу
В)
С)
Задания уровня В
2.1.Ребро куба ABCDA1B1C1D1 равно 6 см. Через диагональ основания BD под углом 45° к
плоскости основания проведена плоскость BDK, пересекающая боковое ребро в точке K.
Найдите площадь треугольника BDK.
[2]
2.2. Найдите угол между вектором (4; -3; 5) и осью ОY.
[3]
86.
2.3 а) Напишите уравнение сферы с центром в начале координат, если плоскость х=6касается этой сферы.
б) Сфера задана уравнением х2 + y2 + z2 -4x + 2y - 6z - 2=0 . Найдите координаты центра
сферы и ее радиус.
[3]
Критерий оценивания
№
Дескриптор
Балл
задания
Применяет свойства параллельных
1.1
Знает взаимное расположение 1
прямых.
прямых.
Использует признак и свойства
параллельности прямой и плоскости.
1.2
Применяет признак и свойства
1.3
параллельности плоскостей,
Использует определение
1.4
перпендикуляра, наклонной и проекции
наклонной в пространстве
Применяет теорему о трех
1.5
перпендикулярах при решении задач
Умеет находить расстояние от точки до
плоскости и между скрещивающимися
прямыми;
Применяет правила сложение векторов
и умножение вектора на число
1.6
Применяет определение коллинеарных
и компланарных векторов в
пространстве
Применяет формулу площади
ортогональной проекции плоской
фигуры на плоскость и применять ее
при решении задач
Применяет формулу нахождения угла
между вектором и осью.
1.8
Применяет формулу для вычисления
уравнение сферы
2.3
Итого
1.7
2.1
2.2
Указать параллельную
прямую, являющеюся линией
пересечения плоскостей.
Обозначить общую прямую
плоскостей.
Вычисляет длину наклонной
1
Вычисляет, используя
теорему о трех
перпендикулярах ,
Выполняет преобразования и
вычисляет расстояние между
точками.
Используя правила сложения
и умножения вектора на
число,вычисляет.
Используя рисунок находит
нужные вектора
1
Выводит формулу
нахождения площади
Вычисляет площадь
треугольника.
Находит длину вектора
Вычислять угол между
вектором и осью
Записывает ответ
1
Записывает уравнение сферы
с центром в начале
координат и данным
радиусом.
Составляет уравнение сферы
Находит координаты и
радиус.
1
1
1
1
1
1
1
1
1
1
1
1
16





































































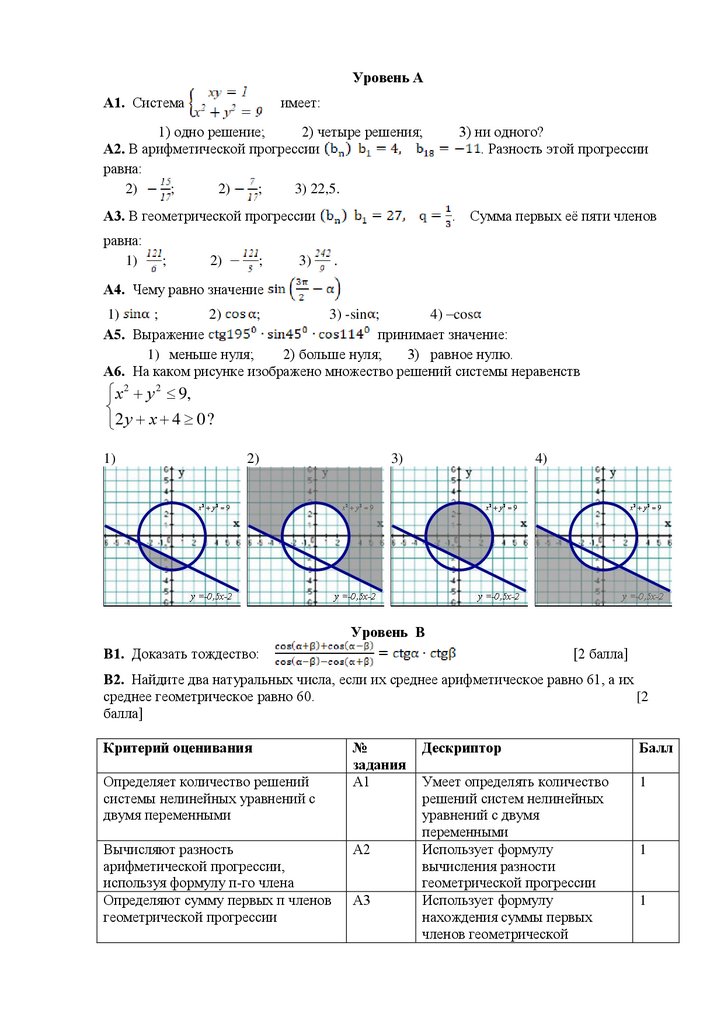








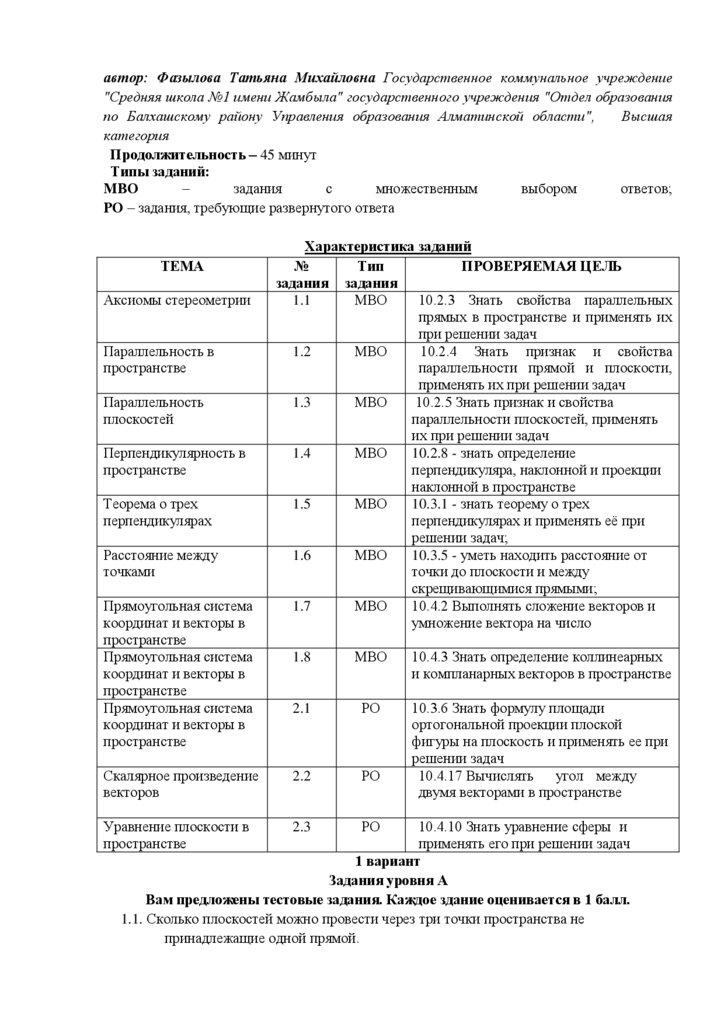





 mathematics
mathematics








