Similar presentations:
Методические рекомендации учителям математики. МО учителей математики
1.
Методические рекомендацииучителям математики
МО учителей математики
2.
Арифметика1. Правило умножения на 11.
2. Правило умножения на 5.
3. Правило умножения на 25.
4. Правило умножения на 125.
10
а 5 а
2
100
а 25 а
4
1000
а 125 а
8
5. Правило возведения в квадрат чисел, оканчивающихся на 5.
3.
Арифметикаabc 100a 10b c
Признаки делимости на 7, 11, 13.
Свойства делимости:
1) делимость суммы и разности;
2) делимость произведения;
3) делимость на произведение.
На какую цифру оканчивается:
п
2
п!
4.
(а + b)3 = a3 + b3 + 3ab (a + b)(а - b)3 = a3 - b3 - 3ab (a - b)
5.
Линейная функцияЛинейные
уравнения
Алгебраическое
условие
Геометрический
вывод
y = к1х+b1
к1 = к2 , b1 ≠ b2
Прямые
параллельны
y = к2х+b2
к1 = к2, b1= b2
Прямые
совпадают
к1 ≠ к2
Прямые
пересекаются
к1 ∙ к2 = -1
Прямые
перпендикулярны
6.
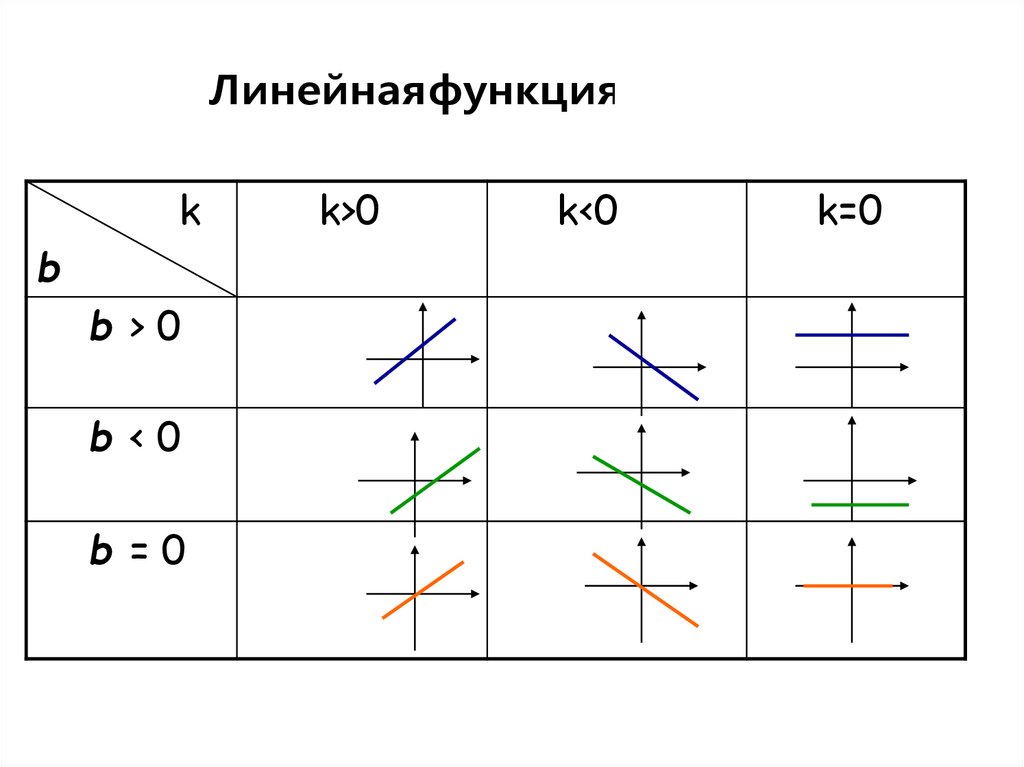
Линейная функцияk
b
b >0
b <0
b =0
k>0
k<0
k=0
7.
8.
Квадратный трехчленах 2 bx c 0
с
1) Если а b c 0, то х1 1, х2
а
с
2) Если b а с, то х1 1, х2
а
Например : 1) 1480 х 2 1490bx 10 0
2) 567 х 2 546bx 21 0
9.
10.
11.
12.
sgn (| f(x)| - | g(x)| ) = sgn ( f 2(x) - g 2(x))Например:
| 5х-3| - | 2х+1| > 0
( 5х-3) 2 - (2х+1) 2 > 0
( 5х – 3 – 2х – 1) ( 5х – 3 + 2х + 1) > 0
13.
b -1sgn log a b sgn
ОДЗ
a - 1
Например
log 2 х ( x 2) log х 3 (3 х ) 0
( x 2 1) (3 х 1
) 0
2 х 1 х 3 1
sgn (a b a c ) sgn a 1 b c
ОДЗ
Например 4
х 2 х 6
16 0
4 1 х 2 х 6 2 0
14.
Теорема 1. Неравенство log a f ( x ) log a g ( x ), где а 0 , a 1,или
log a f ( x ) log a g ( x ) 0 ,
f ( x ) g( x )
0,
а 1
равносильно системе
f ( x ) 0,
g ( x ) 0.
Например log 0,5 ( x 2 4 x ) log 2 ( x 2 3x 4) 0
log 0,5 ( x 2 4 x ) log 0,5 ( x 2 3x 4) 0
( x 2 4 x ) ( x 2 3x 4)
0,
0,5 1
2
x 4 x 0,
x 2 3x 4 0.
15.
Следствие. Неравенствогде а 0 , a 1,b 0 ,
равносильно системе
log a f ( x ) log a g ( x )
0,
log a h( x ) log a b
f ( x ) g( x )
h( x ) b 0 ,
f ( x ) 0,
g( x ) 0,
h( x ) 0.
log 3 5x 2 log 3 2 x 5
Например
0
log 3 x 6 2
5x 2 2 x 5
0,
x 6 9
5х 2 0,
2 x 5 0,
x 6 0.
16.
Теорема 2. Неравенство log a( х ) f ( x ) log a( х ) g ( x )или
log a( х ) f ( x ) log a( х ) g ( x ) 0
f ( x ) g( x )
а( х ) 1 0 ,
f ( x ) 0,
равносильно системе
g( x ) 0,
a( x ) 0;
Например : log x - 2 2 x 3 log x 2 24 6 x 0
2х - 3 - 24 - 6х
0,
х - 2 - 1
x 2 0,
2x 3 0,
24 6x 0.
17.
18.
Теорема 3. Неравенство log f ( х ) а ( x ) log g ( х ) a ( x )a ( x ) 1 f ( x ) g ( x )
f ( х ) 1 g ( x ) 1 0,
f (x) 0
равносильно системе
g ( x ) 0,
a ( x ) 0;
Решить неравенство
log 4 х 2 1 2 x 4 х 5
2
log
2
3 х 4 х 1
x 4 х 5
2
2
log 4 х 2 1 x 2 4 х 5 log 3 х 2 4 х 1 x 2 4 х 5
х 2 4 х 5 1 4 х 2 1 3х 2 4 х 1
0,
2
2
4 х 1 1 3х 4 х 1 1
2
2
4 х 1 0,
3х 2 4 х 1 0,
2
х
4 х 5 0.
19.
20.
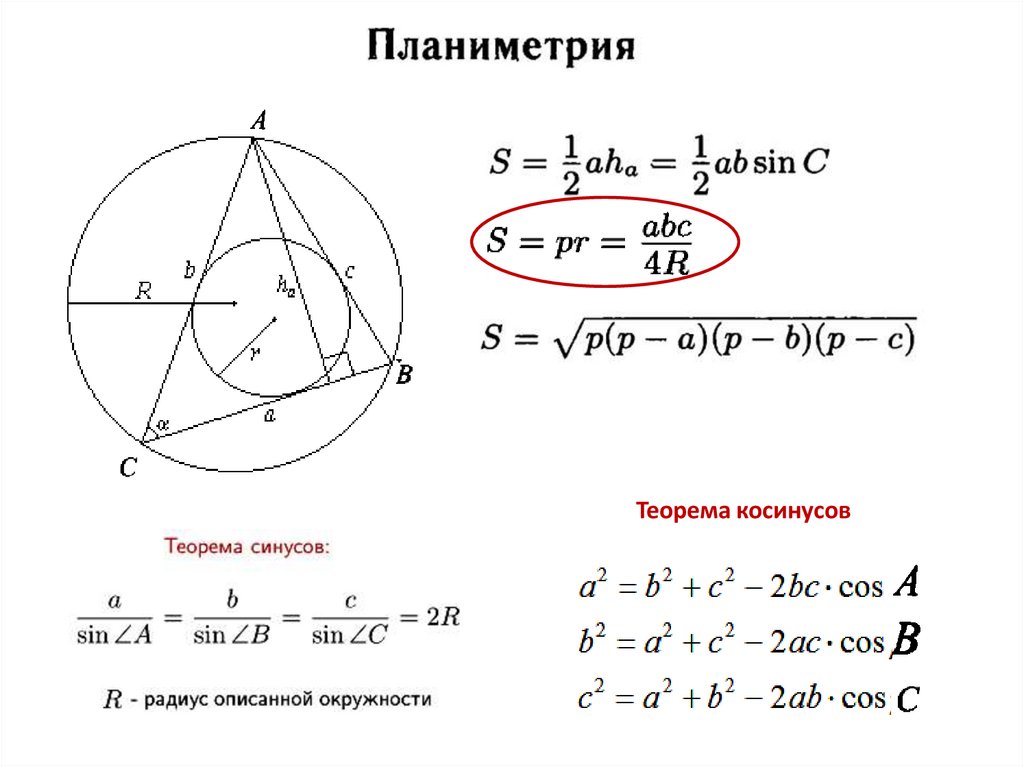
Теорема косинусов21.
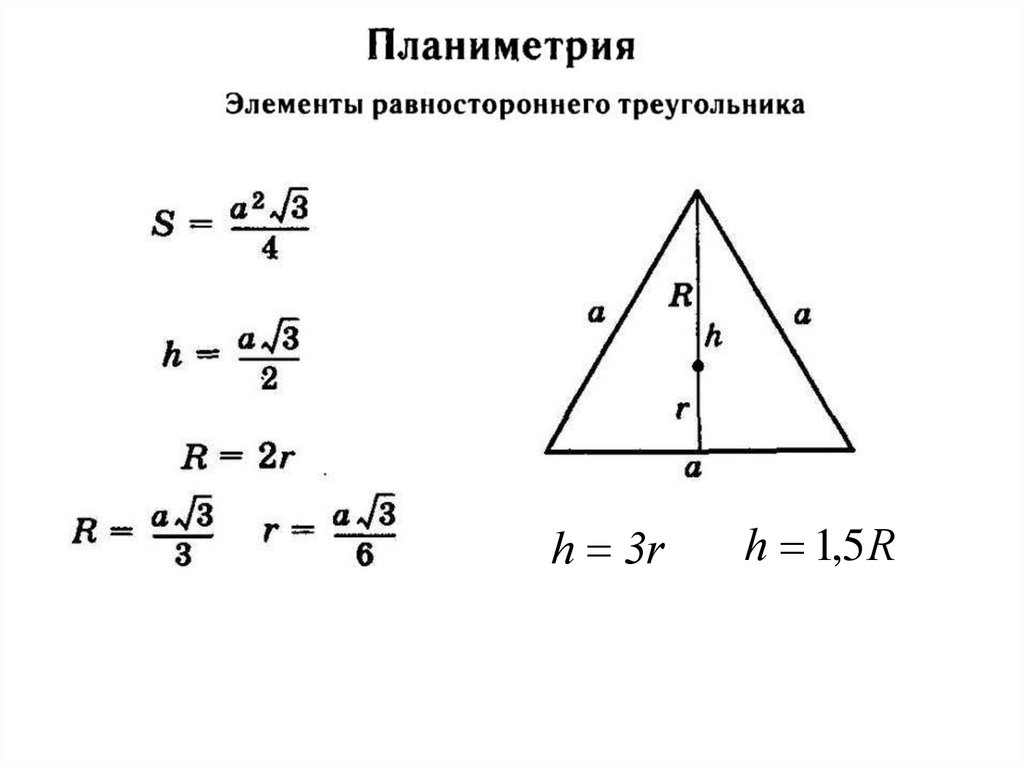
h 3rh 1,5 R
22.
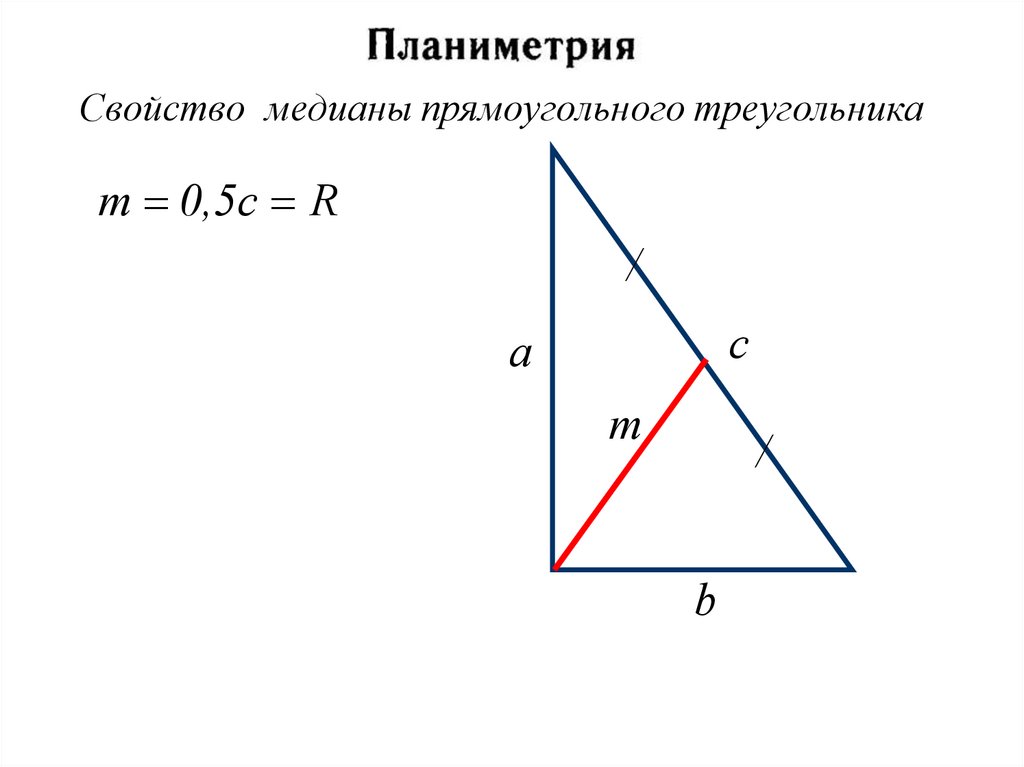
Свойствo медианы прямоугольного треугольникаm 0,5с R
/
с
a
m
/
b
23.
24.
Свойства параллелограммаБиссектриса параллелограмма отсекает равнобедренный треугольник.
В параллелограмме со сторонами a,b и диагоналями d 1 и d 2
выполняется равенство : 2а 2 2b 2 d 12 d 22
25.
26.
6. Если около трапеции можно описать окружность, то этатрапеция равнобедренная.
27.
28.
29.
30.
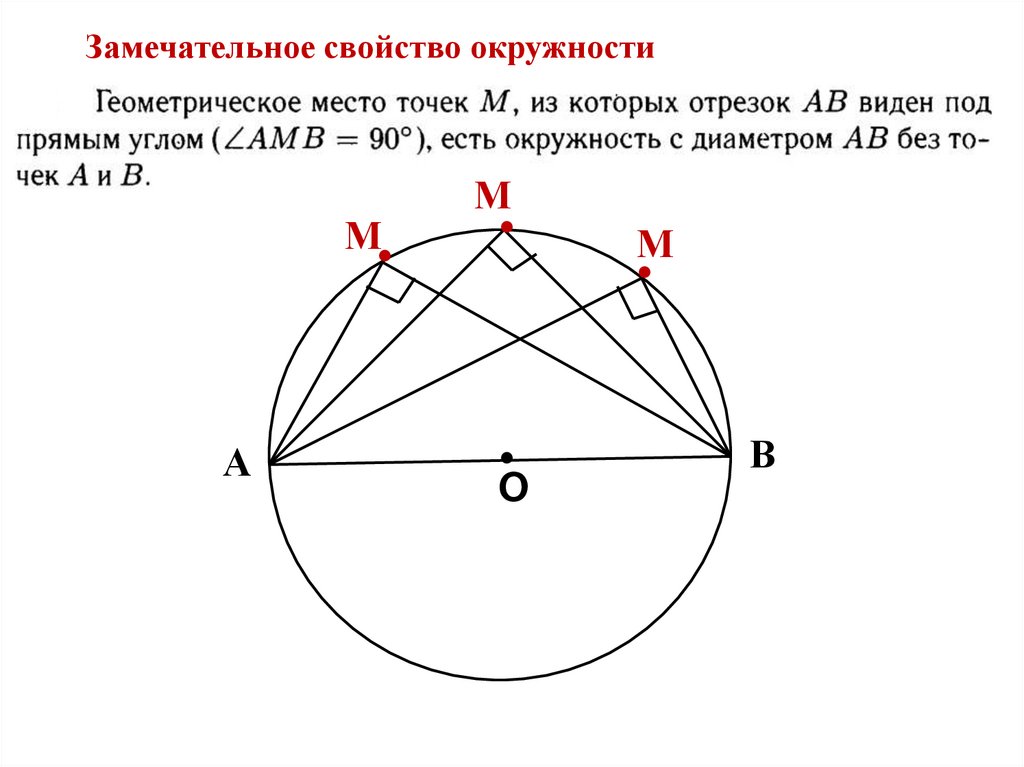
Замечательное свойство окружностиМ
.
А
М
.
.
О
М
.
В

























 mathematics
mathematics








