Lecture 7

1.

Physics 2
Voronkov Vladimir Vasilyevich

2. Lecture 7

• Blackbody Radiation
• Stefan-Boltzmann’s Law
• Rayleigh-Jeans Formula
• Planck Formula
• Wien’s Displacement Law
• Photoelectric Effect
• Compton’s Effect

3.

• All objects radiate energy continuously
in the form of electromagnetic waves
produced by thermal vibrations of the
molecules.
• Example: the orange glow from an
electric stove burner, an electric space
heater, or the coils of a toaster.

4. A blackbody

• A black body absorbs all light that falls on it. No
electromagnetic radiation passes through it and none is
reflected so the object appears black when it is cold. The light
emitted by a black body is called black-body radiation.
• If the black body is hot, these properties make it an ideal
source of thermal radiation. If a perfect black body at a certain
temperature is surrounded by other objects in thermal
equilibrium at the same temperature, it will on average emit
exactly as much as it absorbs, at every wavelength.
• The radiation in such an environment has a spectrum that
depends only on T, the temperature of the object is directly
related to the wavelengths of the light that it emits.
• At room temperature, black bodies emit infrared light, but as
the temperature increases, black bodies start to emit at visible
wavelengths, from red, through orange, yellow, and white
before ending up at blue, beyond which the emission includes
increasing amounts of ultraviolet.

5.

• The hole acts as a nearly ideal black-body
radiator. This makes peepholes into furnaces
good sources of blackbody radiation, and
sometimes we call it cavity radiation for this
reason.
• "Blackbody radiation" or "cavity radiation" refers
to an object or system which absorbs all
radiation incident upon it and re-radiates energy
which is characteristic of this radiating system
only, not dependent upon the type of radiation
which is incident upon it.

6. Stefan-Boltzmann law

The rate at which an object radiates energy is proportional
to the fourth power of its absolute temperature:
P is the power in watts radiated from the surface of the
object,
s=5.67 *10-8 W/(m2K4) is a constant,
A is the surface area of the object in m2,
e is the emissivity: 0≤e≤1, depending on the properties of
the surface of the object.
T is the surface temperature in kelvins.
The emissivity is equal to the absorptivity, which is the
fraction of the incoming radiation that the surface absorbs.

7.

As an object radiates energy at a rate given by the
Stefan’s law, it also absorbs electromagnetic
radiation. If the latter process did not occur, an
object would eventually radiate all its energy, and
its temperature would reach absolute zero. The
energy an object absorbs comes from its
surroundings, which consist of other objects that
radiate energy. If an object is at a temperature T
and its surroundings are at an average
temperature T0, then the net rate of energy gained
or lost by the object as a result of radiation is

8.

• When an object is in equilibrium with its
surroundings, it radiates and absorbs energy at the
same rate, and its temperature remains constant.
When an object is hotter than its surroundings, it
radiates more energy than it absorbs, and its
temperature decreases.
• A black body (or ideal absorber) is defined as an
object that absorbs all the energy incident on it, and
for such an object, e = 1.
• A black body is also an ideal radiator of energy.
• In contrast, an object for which e = 0 absorbs none of
the energy incident on it. Such an object re ects all
the incident energy, and thus is an ideal re ector.

9. Stefan-Boltzmann’s law for a black body

So for a black body e=1, then:
P=sAT4
P is the power in watts radiated from the surface of
the object,
s=5.669 6 *10-8 W/(m2K4) is a constant,
A is the surface area of the object in m2

10. Rayleigh-Jeans formula

For a black body radiation:
f is the frequency of the radiated energy
T is the temperature of the surface
u is the energy density function (in J/m3): the energy
in a small interval of frequencies [f; f+df] is u(f,t)df.
- This formula is correct only for low
frequencies.
- This formula is incorrect for high
frequencies.

11.

The Rayleigh-Jeans formula is derived on the basis of
classical thermodynamic statistics saying that energy
is distributed uniformly by the degrees of freedom.
According to Rayleigh-Jeans formula the radiated
energy density is proportional to the square of the
frequency:
u ~ f2
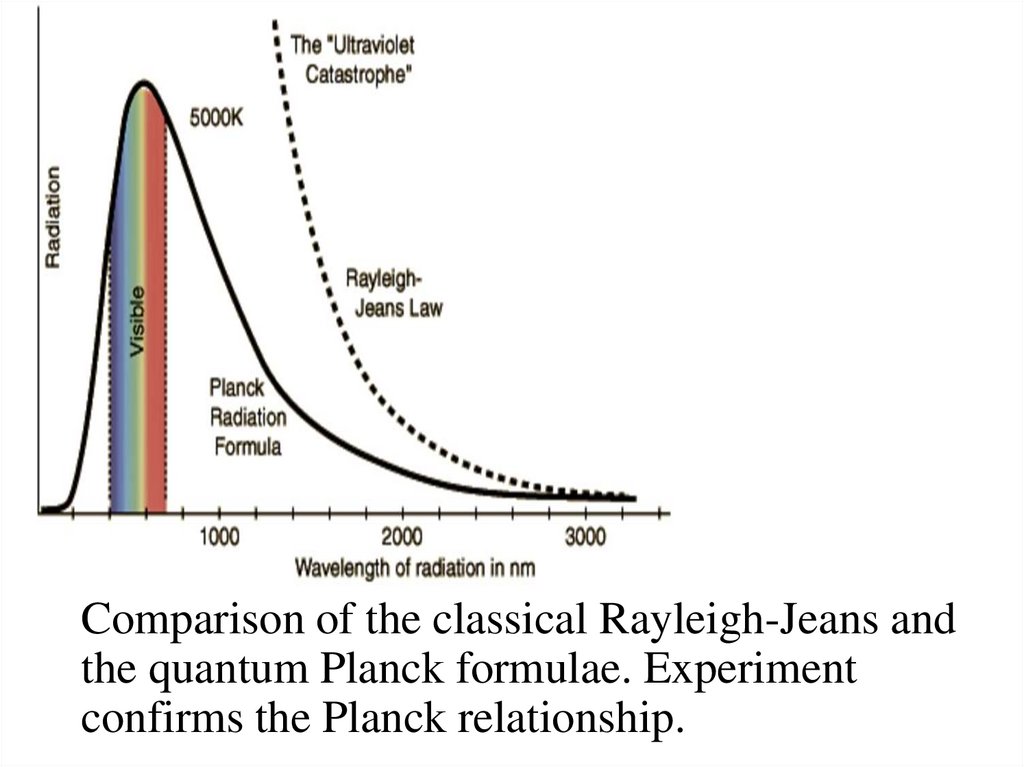
So for high frequencies this formula predicts
continual increase in radiated energy with frequency,
because of the continually repeating process of
absorption and emission. This failed prediction is
called the “ultraviolet catastrophe”.

12. Planck formula

u(f,t) is the energy-density function,
h=6.625·10-34 J·s_ is the Planck’s constant,
c=2.997*108 m/s is the speed of light
k=1.38·10-23 J/K is the Boltzmann’s constant
f is the frequency of emitted radiation
T is the temperature of the black body surface

13. The quantum nature of radiation

Planck derived his formula by making an assumption
that the walls of the cavity constantly absorb and
reemit the radiation, and the absorption and emission
of radiation was limited to "bundles" of energy. Each
bundle had an energy proportional to its frequency,
according to the formula:
E=hf
This assumption was interpreted by Einstein:
Electromagnetic radiation consists of quanta, or
identical, indivisible units, each carrying energy hf,
where f is the frequency of the radiation.

14.

These quanta, or photons moves with the speed
of light c, their energy is E=hf, then the
momentum p and the wavelength l of a photon
is:
p=E/c=hf/c
l=c/f=hc/E=h/p
l=h/p
This formula, connecting the wavelength and
momentum of a particle, is a sheer evidence of
dualism of light: it unites wave and quantum
properties.

15. Planck and Stefan-Boltzmann formulae

The Stefan-Boltzmann’s formula for total
radiation
P=sAT4
can be obtained from the Planck’s formula
by integrating it over all frequencies f.

16. Planck and Rayleigh-Jeans formulae

For small f, when hf << kT:
Thus, when the thermal energy is higher than
the energy of a photon, then the classical
approach is valid.

17.

Comparison of the classical Rayleigh-Jeans and
the quantum Planck formulae. Experiment
confirms the Planck relationship.

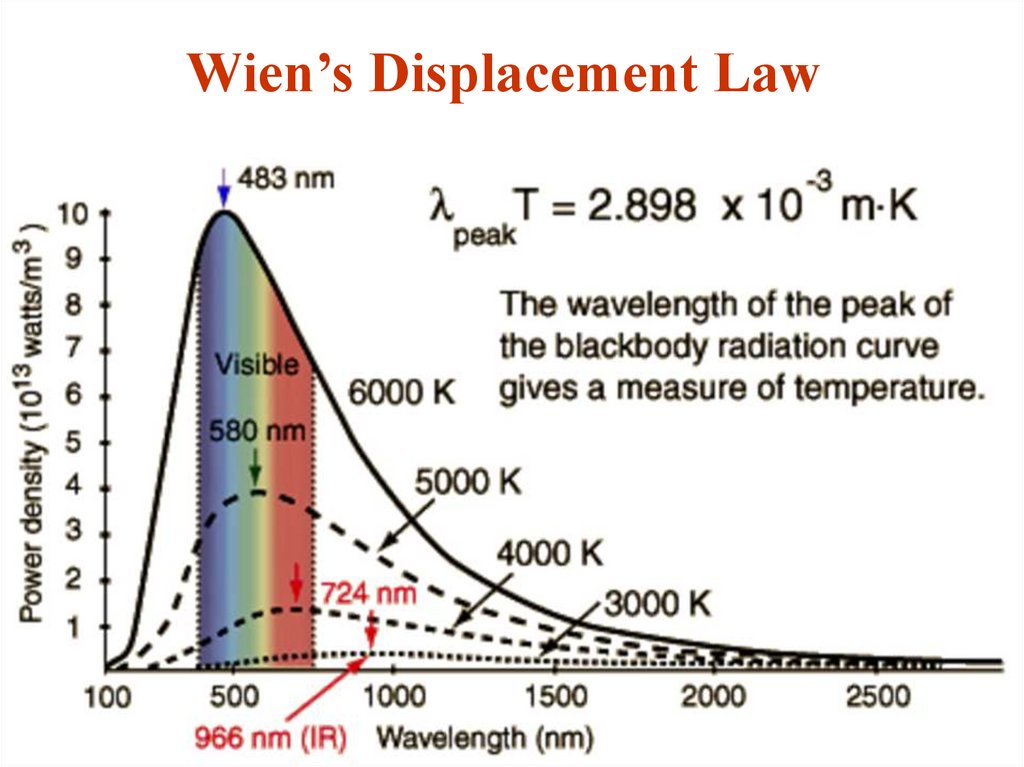
18. Wien’s Displacement Law

19.

Wien’s displacement law says that the
wavelength of the peak of the blackbody
radiation curve decreases in a linear fashion as
the temperature increases:
lm=b/T
b=2.898·10-3 m·K

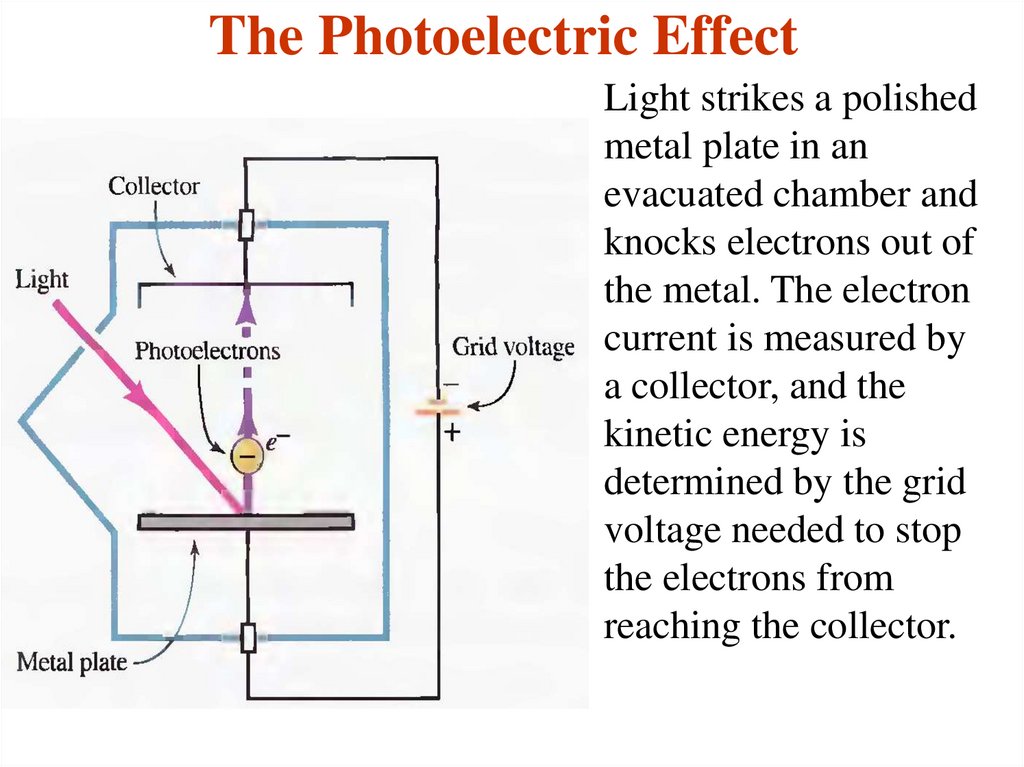
20. The Photoelectric Effect

Light strikes a polished
metal plate in an
evacuated chamber and
knocks electrons out of
the metal. The electron
current is measured by
a collector, and the
kinetic energy is
determined by the grid
voltage needed to stop
the electrons from
reaching the collector.

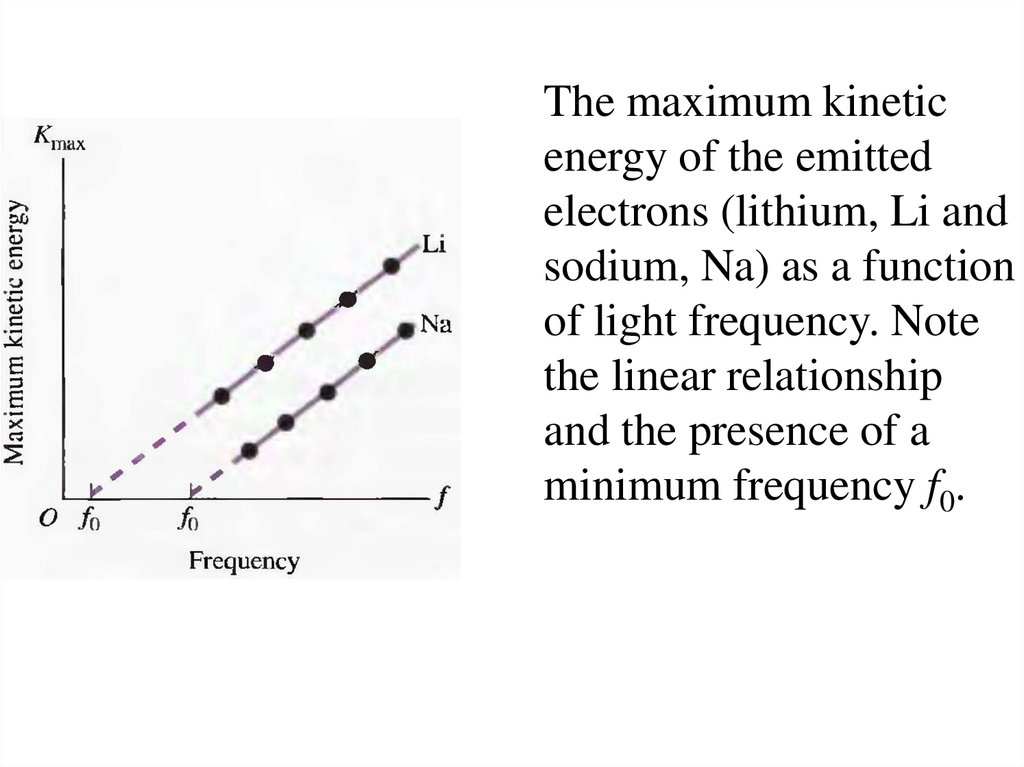
21.

The maximum kinetic
energy of the emitted
electrons (lithium, Li and
sodium, Na) as a function
of light frequency. Note
the linear relationship
and the presence of a
minimum frequency f0.

22.

• When a polished metal plate is exposed to
electromagnetic radiation, it may emit electrons, but
not positive ions. These electrons are sometimes
called photoelectrons.
• Electrons will be emitted only if the frequency of the
incident light exceeds a threshold value – that is f>f0.
The value of f0 varies with the particular metal.
• The magnitude of the emitted current of electrons
is proportional to the intensity of the light source but
does not depend on the frequency.
• The energy of the emitted electrons is independent
of the intensity of the light source but varies linearly
with the frequency of the incident light.

23.

Einstein explained these phenomena by postulating
that electrons are emitted because individual
electrons absorb individual photons.
E = hf – the energy of a photon,
W – the minimum energy required to liberate an
electron from the metal,
if hf < W then no electrons will be emitted,
if hf > W then electron can be emitted with the kinetic
energy:

24.

• The quantity W is a potential energy that must be
acquired before the electron can be liberated; it is called
the work function. The work function is a characteristic
of the particular metal that emits electrons, typically
taking on a value in the range of several eV. (1 eV = 1.6
·10-19 J).
• It takes one photon to liberate one electron. Therefore,
the current of emitted electrons is proportional to the
intensity of the radiation because the intensity is
proportional to the number of photons in the
electromagnetic wave.
• An electron absorbs a photon almost instantaneously,
that’s why there is no measurable time delay between the
arrival of the radiation and the appearance of the electron
current.

25. Compton Effect

Compton’s experiment. The scattered X rays are
diffracted by a crystal, with the angle a used to
determine the wavelength of the scattered radiation.

26.

Compton sent x-rays (1017 <f < 1020 Hz) through thin metallic foils
and observed scattered rays with 2 wavelengths: λ0 – incident
radiation and with a longer λ`:
m is the mass of electron,
θ is the scattering angle,
h/(mc)=2.4·10-12 m is the Compton wavelength of the electron.
This result contradicts the prediction of classical radiation theory, in
which the electrons absorb radiation and reradiate it as without any
change in wavelength.
Compton considered the photon as a particle with E= hf and p=E/c
which collides elastically with a target electron.
The electron final energy is:
The energy of scattered photon differs from that of the incident photon
so the wavelength is also different.
So this experiment confirmed the particle nature of radiation.

27.

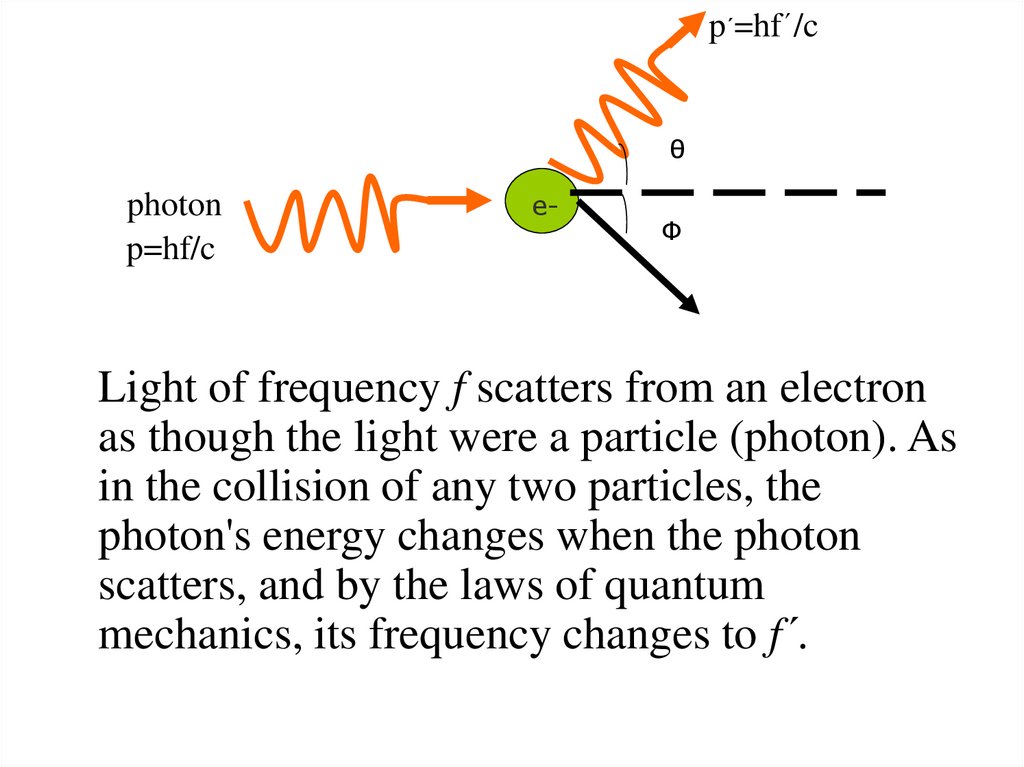
p´=hf´/c
θ
photon
p=hf/c
e-
Φ
Light of frequency f scatters from an electron
as though the light were a particle (photon). As
in the collision of any two particles, the
photon's energy changes when the photon
scatters, and by the laws of quantum
mechanics, its frequency changes to f´.

28.

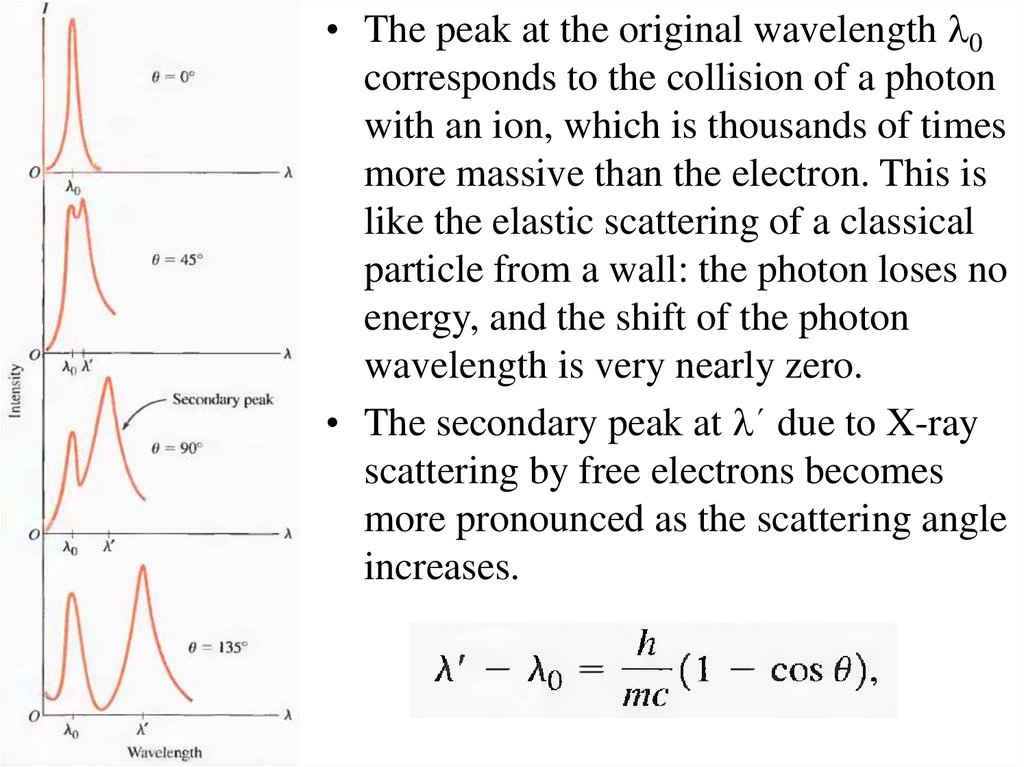
• The peak at the original wavelength l0
corresponds to the collision of a photon
with an ion, which is thousands of times
more massive than the electron. This is
like the elastic scattering of a classical
particle from a wall: the photon loses no
energy, and the shift of the photon
wavelength is very nearly zero.
• The secondary peak at l´ due to X-ray
scattering by free electrons becomes
more pronounced as the scattering angle
increases.

29. Electro-Magnetic Radiation Dualism

• Experiments such as the scattering of X
rays from matter, designed to study the
particle nature of radiation, do in fact see
radiation exhibiting particle behavior.
• At the same time, experiments that probe
the wave character of radiation, such as
interference experiments, confirm the
wave character of radiation.
• It shows that electro-magnetic radiation
has a dual wave-particle nature.

30. Units in Si

Wien’s constant
Planck’s constant
Planck’s constant
Boltzmann’s constant
Stefan-Boltzmann constant
b
2.898·10-3 m·K
h
6.626·10-34 J·s
ћ=h/(2p)
1.055·10-34 J·s
kB
1.38·10-23 J/K
s
5.67 *10-8 W/(m2K4)