Similar presentations:
Элементы квантовой механики атомов. Лекция 31
1.
Часть 5. Квантовая физикаЛекция 31. Элементы квантовой
механики атомов
2.
1. Атом водорода в квантовой механике2. Квантовые числа
3. Спин электрона
4. Принцип Паули
5. Распределение электронов в атоме по
состояниям
6. Периодическая
Менделеева
система
элементов
3.
Дополнение механической планетарной модели атомаРезерфорда постулатами Бора позволило достаточно
убедительно объяснить и описать линейчатый спектр
атома водорода.
Самой слабой стороной теории атома водорода Бора
была её внутренняя логическая противоречивость,
поскольку в ней использовались два принципиально
различных подхода:
понятие непрерывной
электрона в атоме
Ньютона:
траектории
классической
движения
механики
4.
представлениео
дискретных
состояниях атома.
квантовых
Дальнейшее развитие квантовой механики привело к
отказу от механической картины движения электрона в
кулоновском поле ядра.
Планетарная модель атома была заменена квантовомеханическим описанием его строения, базирующимся
на волновых свойствах вещества.
5.
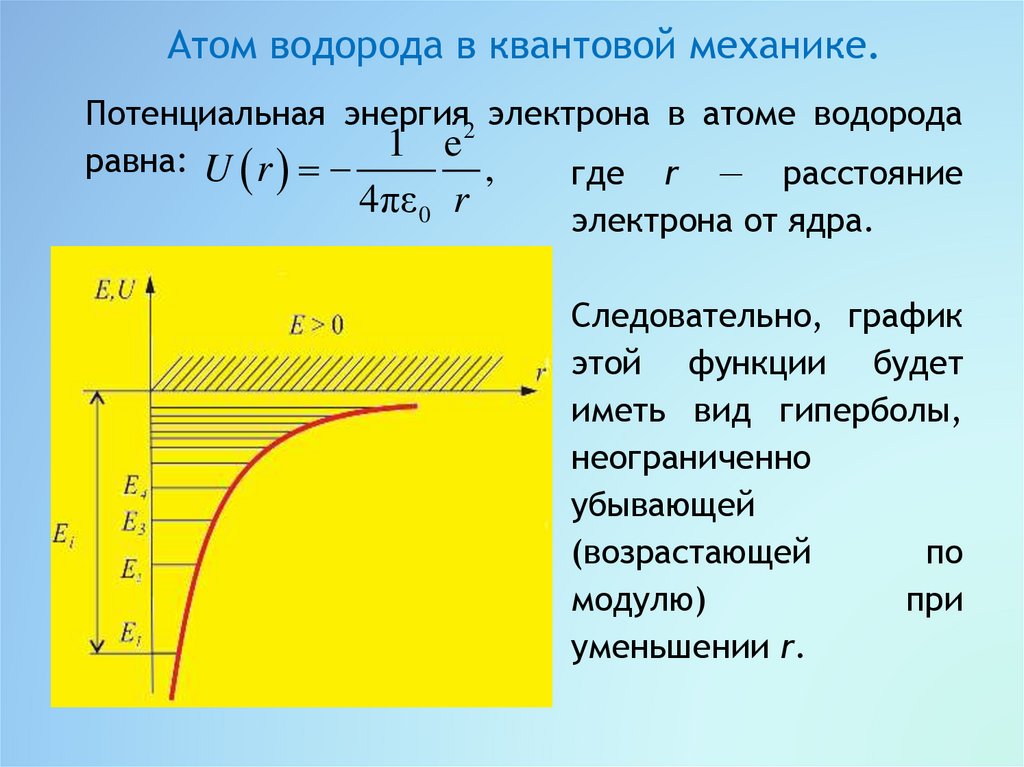
Атом водорода в квантовой механике.Потенциальная энергия2 электрона в атоме водорода
равна: U r 1 e ,
где r — расстояние
4πε 0 r
электрона от ядра.
Следовательно, график
этой функции будет
иметь вид гиперболы,
неограниченно
убывающей
(возрастающей
по
модулю)
при
уменьшении r.
6.
Состояниеэлектрона
в
атоме
определяется волновой функцией
удовлетворяющей
стационарному
Шредингера:
водорода
r ,
уравнению
2me
1 e2
2 E
0.
4πε 0 r
Не вдаваясь в математические подробности решения
этого уравнения, ограничимся анализом важнейших
результатов, которые из него следуют.
7.
Энергия. Записанное выше уравнение имеетрешения,
удовлетворяющие
требованиям
однозначности,
конечности
и
непрерывности
волновой пси-функции только при дискретных
отрицательных собственных значениях энергии,
равных
2
1 mee 4 1
En
2
2
4πε 0 2 n
Возможные значения
Е1,
приведённом выше графике
горизонтальных прямых.
n 1,2,3,... .
Е2,..
показаны на
U r
в виде
8.
Из графика следует, что по мере роста главногоквантового
числа
n
энергетические
уровни
располагаются теснее и при n E 0.
Самый нижний уровень Е1 при n = 1 называется
основной, все остальные (n > 1) — возбуждённые.
При Е < 0 «движение» электрона является связанным —
он находится внутри гиперболической потенциальной
ямы.
При
Е > 0
«движение» электрона становится
свободным,
эта
область
соответствует
ионизированному атому.
9.
Квантовые числаОказалось, что состояние электрона в атоме водорода
характеризуется определенным набором квантовых
чисел.
Главное квантовое число n определяет энергетические
уровни электрона в атоме и может принимать любые
целочисленные значения начиная с единицы:
n = 1, 2, 3, …
Орбитальное квантовое число l , которое при заданном
значении n может принимать значения
l = 0, 1, 3, …, (n — 1),
10.
характеризует геометрию орбиты электрона (еёэллиптичность) и определяет дискретный набор
возможных значений механического орбитального
момента импульса электрона:
Le
l l 1 .
Из решения уравнения Шредингера следует также, что
вектор момента импульса электрона Le может иметь
такие ориентации в пространстве, при которых его
проекция на направление z внешнего магнитного поля
принимает квантованные значения:
Lez ml ,
11.
где ml— магнитное квантовое число, которое при
заданном l может принимать квантованные значения:
ml 0, 1, 2, ..., l.
Таким
образом,
каждому
значению
главного
квантового числа n, определяющему энергетическое
состояние атома, соответствует ряд комбинаций
квантовых чисел l и ml.
Каждой
такой
комбинации
соответствует
определённое
распределение
вероятности
обнаружения
электрона
в
различных
точках
пространства («электронное облако»).
12.
Квантовые числа n и l характеризуют размер и формуэлектронного облака, а квантовое число ml
—
ориентацию электронного облака в пространстве.
Число различных состояний, соответствующих данному
n, равно
n 1
2
2
l
1
n
.
l 0
Область пространства, в которой высока вероятность
обнаружения электрона, называют орбиталью.
13.
В квантовой механике принято называть состоянияэлектрона, характеризующиеся квантовыми числами
l = 0 s-состояниями,
l = 1 — p-состояниями,
l = 2 — d-состояниями,
l = 3 — f-состояниями и т. д.
Значение главного квантового числа указывается перед
условным обозначением орбитального квантового числа.
Например, электроны в состояниях с n = 2 и l = 0 и l = 1
обозначаются соответственно символами 2s и 2р.
14.
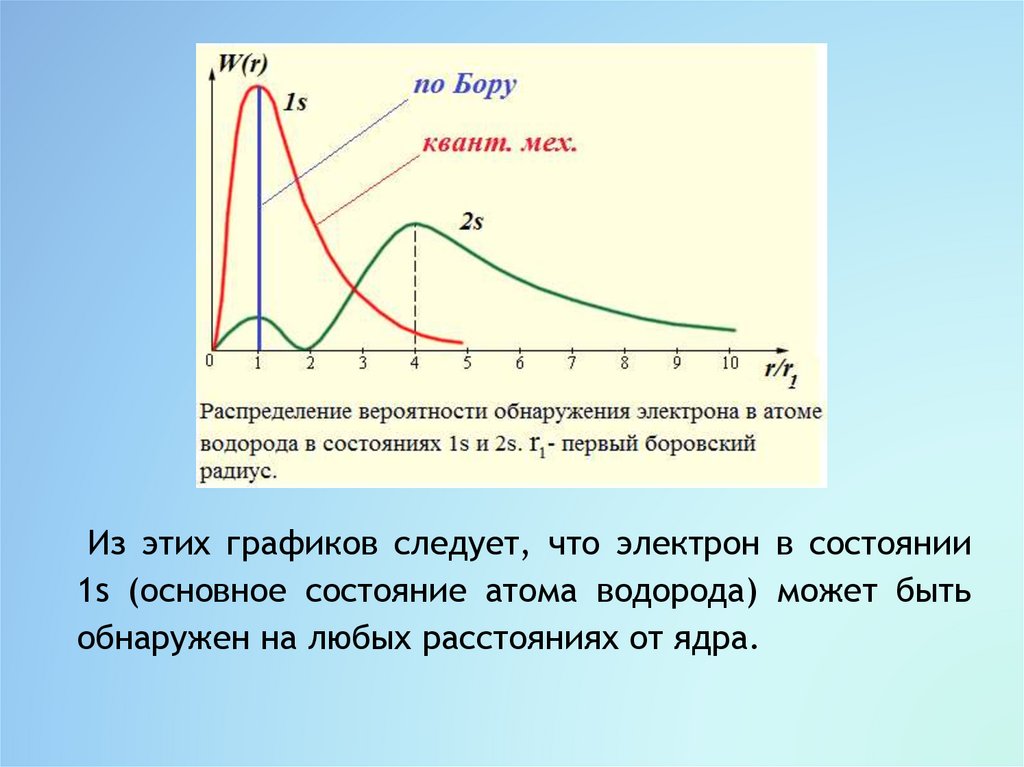
По теории Бора вероятность нахождения электронапри любых значениях r r1 равна нулю, тогда как
квантовая механика допускает нахождение электрона и
на других расстояниях от ядра, но с меньшей
вероятностью, чем при r r1.
Согласно квантовой механике боровские орбиты
электрона представляют собой геометрическое место
точек, в которых с наибольшей вероятностью может
быть обнаружен электрон.
15.
Из этих графиков следует, что электрон в состоянии1s (основное состояние атома водорода) может быть
обнаружен на любых расстояниях от ядра.
16.
С наибольшей вероятностью его можно обнаружить нарасстоянии, равном радиусу r1 первой боровской
орбиты.
Вероятность обнаружения электрона в состоянии 2s
максимальна на расстоянии r 4r1 от ядра.
В обоих случаях атом водорода можно представить в
виде сферического симметричного электронного
облака, в центре которого находится ядро.
При l > 1 сферическая симметрия электронного облака
нарушается.
17.
Боровскихорбит
в
атоме
водорода
в
действительности не существует.
В каждом состоянии может быть определено только
распределение вероятности нахождения электрона
на различных расстояниях от ядра, которое называют
электронным облаком.
18.
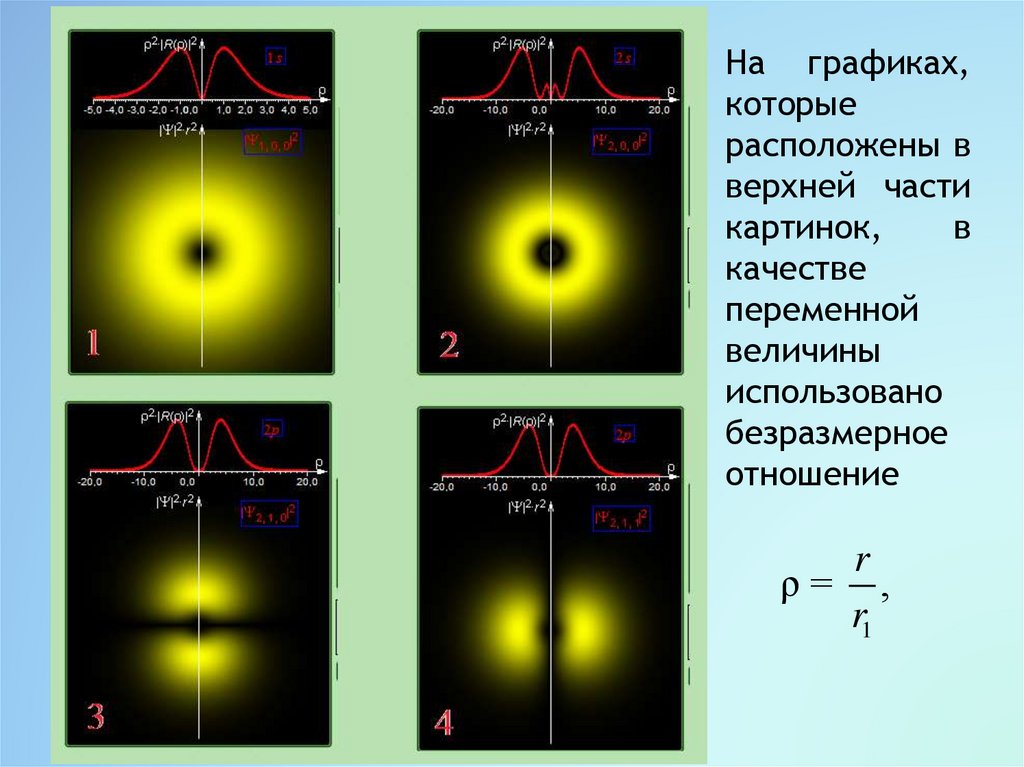
На графиках,которые
расположены в
верхней части
картинок,
в
качестве
переменной
величины
использовано
безразмерное
отношение
r
ρ= ,
r1
19.
20.
Спин электронаВ 1922 году О. Штерн и В. Герлах в опытах по
измерению магнитных моментов атомов различных
химических элементов обнаружили новое явление.
Оказалось, что узкий пучок атомов водорода,
находящихся в s-состоянии (проекция орбитального
момента импульса электрона на направление внешнего
магнитного поля равна нулю), в неоднородном
магнитном поле расщеплялся на два пучка.
21.
Возник вопрос, пространственное квантованиекакого момента импульса обнаружилось в этих
опытах?
В 1925 году молодые американские физики Д. Уленбек
и С. Гаудсмит теоретически объяснили расщепление
спектральных линий, предположив существование у
электрона собственного механического момента
импульса (спина), не связанного с пространственным
движением электрона.
22.
Спин электрона Ls (и всех других микрочастиц) —квантовая величина, у нее нет классического
аналога.
Это внутреннее свойство микрочастицы, подобное её
заряду или массе.
Спин электрона имеет только одно значение
Ls
2
3,
а проекция спина на направление внешнего
магнитного поля определяется выражением:
23.
Lsz ms ,1
где ms — магнитное спиновое квантовое число.
2
Таким образом, для полного описания состояния
электрона в атоме необходимо задать набор из четырех
квантовых чисел:
главного n, (1, 2, 3, …);
орбитального l, (0, 1, 2, …, (n —1));
магнитного ml (0, ±1, ±2, …, ±l);
магнитного спинового ms (±1/2).
24.
Принцип ПаулиЗадание набора квантовых чисел
для
описания
состояния
электронов
имеет
более
существенное
значение,
чем
просто
классификация
их
состояний.
Вольфганг Паули
В 1925 году швейцарский физик
В. Паули открыл закон, известный
под названием принцип Паули или
принцип запрета:
25.
в одном и том же атоме не может быть более одногоэлектрона с одинаковым набором четырёх квантовых
чисел n, l, ml, ms.
0
Z n, l , ml , ms
1
где Z n, l , ml , ms — число электронов, находящихся в
квантовом состоянии, описываемых набором четырёх
квантовых чисел: n, l , ml , ms .
26.
Распределение электроновв атоме по состояниям
Максимальное число электронов, находящихся в
состояниях,
определяемых
значением
главного
квантового числа n, равно
n 1
Z n 2 2l 1 2n 2 .
l 0
Совокупность электронов в многоэлектронном атоме,
имеющих одно и то же главное квантовое число,
называют электронной оболочкой.
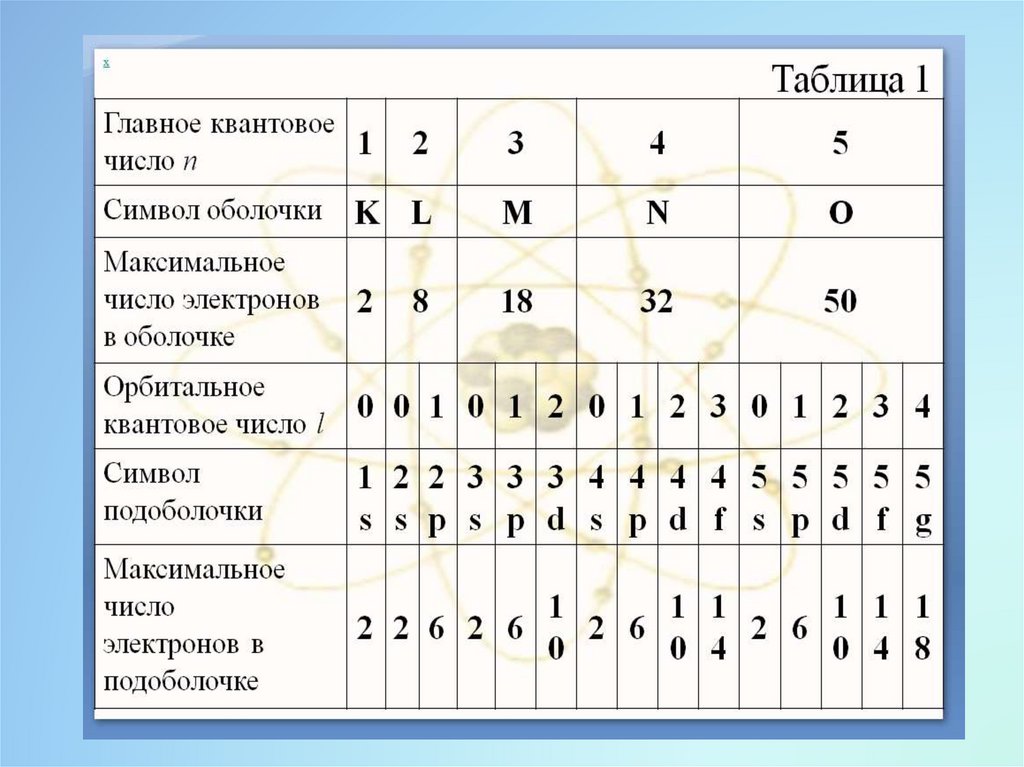
27.
В каждой из оболочек электроны распределяются поподоболочкам, соответствующим данному значению l.
Число подоболочек равно порядковому номеру
оболочки, т. к. l принимает значения от 0 до n — 1.
n
Количество электронов в подоболочке с заданным l
определяется магнитным орбитальным и магнитным
спиновым квантовыми числами:
Z l 2 2l 1 .
Обозначение оболочек, распределение электронов по
оболочкам и подоболочкам в атомах приведено в таблице
1 ниже.
28.
29.
Периодическая системаэлементов Менделеева
Д.И. Менделеев
Принцип Паули, лежащий в
основе
систематики
заполнения
электронных
состояний в атомах, позволяет
объяснить
Периодическую
систему
элементов Д. И.
Менделеева
—
фундаментальный
закон
природы,
являющийся
основой современной химии,
атомной и ядерной физики.
30.
Теория периодическойследующих положениях:
системы
основывается
на
общее число электронов в атоме данного
химического элемента равно порядковому номеру Z
элемента;
каждый последующий элемент образован из
предыдущего прибавлением к ядру одного протона и
одного электрона к электронной оболочке;
состояние электрона в атоме определяется набором
четырех квантовых чисел: n, l , ml , ms ;
31.
распределение
электронов
в
атоме
по
энергетическим
состояниям
удовлетворяет
принципам Паули и минимума потенциальной
энергии:
с
возрастанием
числа
электронов
каждый
следующий электрон должен занять возможное
энергетическое состояние с наименьшей энергией;
• взаимодействием электронов пренебрегаем.
32.
Z = 1 (водород, Н)Единственный электрон атома водорода находится в
состоянии 1s, характеризуемом квантовыми числами n =
1, l = 0, ml = 0
ms = 1/2 (ориентация спина произвольна).
Z = 2 (гелий, Не)
Оба электрона атома гелия находятся в состоянии 1s с
антипараллельной ориентацией спина. Электронная
конфигурация записывается в виде 1s2 (два 1s
электрона). На атоме гелия заканчивается заполнение Коболочки, что соответствует завершению первого
периода таблицы).
33.
Z = 3 (литий, Li)Третий электрон атома лития согласно принципу
Паули уже не может быть размещен в целиком
заполненной К-оболочке и поэтому занимает наинизшее
энергетическое состояние в следующей L-оболочке с
n = 2, т. е. 2s-состояние. Электронная конфигурация
для атома лития 1s22s. Атом лития начинает второй
период системы элементов.
Z = 4 (бериллий, Ве)
Четвёртым
электроном
бериллия
заканчивается
заполнение подоболочки 2s. У следующих шести
элементов от Z = 5 (бор, В) до Z = 10 (неон, Ne) идёт
заполнение подоболочки 2р.
34.
Z = 11 (натрий, Na)Одиннадцатый электрон натрия размещается в Моболочке (n = 3), занимая наинизшее энергетическое
состояние 3s. Электронная конфигурация имеет вид:
1s22s22p63s Как и 2s электрон атома лития электрон 3s
атома натрия является валентным электроном, поэтому
физические и химические свойства натрия и лития
схожи.
Таким
образом,
открытая
Менделеевым
периодичность в химических свойствах элементов
объясняется
повторяемостью
в
структуре
внешних
оболочек
у
атомов
родственных
элементов.
35.
Так инертные газы (He, Ne, Ar, Kr, Xe, Rn) имеютодинаковые внешние оболочки из 8-ми электронов в sи р-состояниях.
Во внешней оболочке щелочных металлов (Li, Na, K,
Rb, Cs, Fr) имеется лишь один s-электрон; во
внешней оболочке щелочно-земельных элементов (Be,
Mg, Ca, Sr, Ba, Ra) имеются два s-электрона, галоиды
(F, Cl, Br, I, At) имеют внешние оболочки, в которых
недостаёт одного электрона до оболочки инертного
газа.
36.
37.
Квантоваятрактовка
периодической
системы
позволила понять природу химических связей.
Ионная (гетерополярная) связь
образуется
при
объединении в молекулу атомов, к которых общее
количество электронов во внешнем слое равно 8
(например, NaCl). При этом один из атомов отдаёт свой
электрон (Na), и превращается в положительный ион, а
другой,
приобретая
электрон,
становится
отрицательным
ионом
(Cl).
Их
электрическое
взаимодействие позволяет образовываться устойчивой
молекуле.
38.
Ковалентная (гомеополярная) связь возникает присближении атомов с антипараллельными спинами
(например, атомы Н). В результате действия сил
притяжения между атомами возникает устойчивая
молекула.


































 physics
physics








