Similar presentations:
Дифференциал функции нескольких переменных
1.
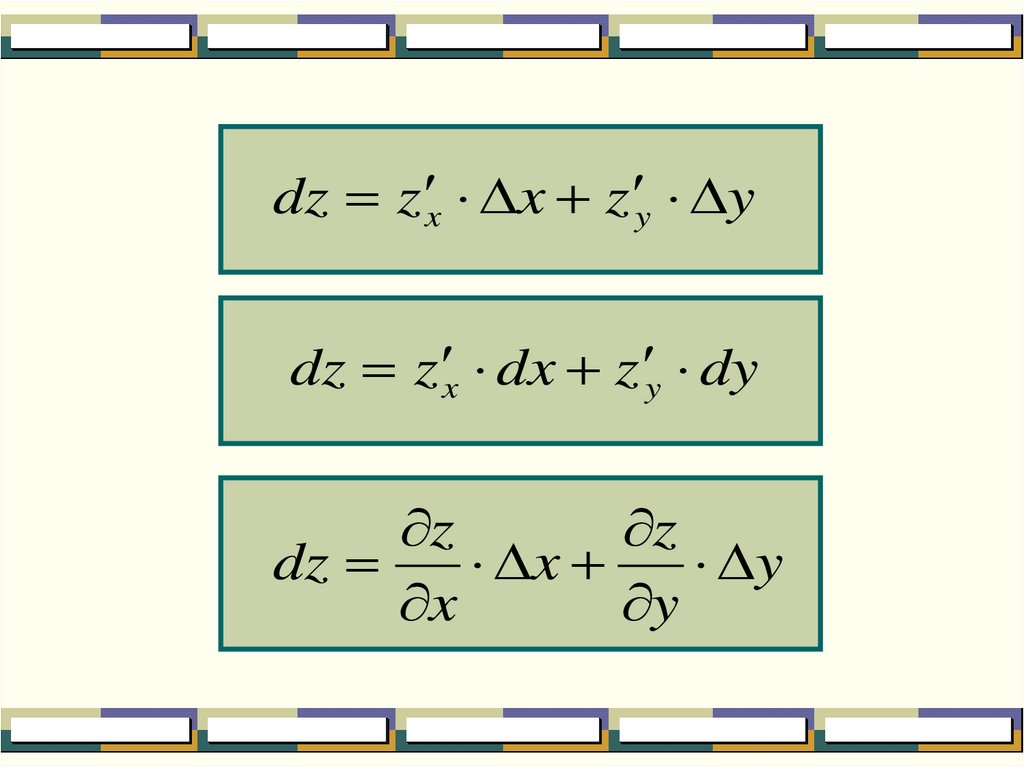
Дифференциалом функции называетсясумма произведений частных
производных этой функции на
приращения соответствующих
независимых переменных.
2.
dz z x x z y ydz z x dx z y dy
z
z
dz
x
y
x
y
3.
Функция z=f(x,y) называетсядифференцируемой в точке (x,y), если
ее полное приращение можно
представить в виде:
z dz x y
4.
Где dz – дифференциал функции;( x, y )
( x , y )
- бесконечно малые величины при
x 0
и
y 0
Таким
образом,
дифференциал
функции
нескольких переменных – это главная, линейная
относительно приращений Δх и Δу часть полного
приращения функции.
5.
Дляфункции
одной
переменной
существование конечной производной
y=f(x)
f (x )
и представление приращения функции в виде
y dy ( x) x
являются равнозначными утверждениями.
Для
функции
нескольких
переменных
существование частных производных является
необходимым но не достаточным условием
дифференцируемости функции.
6.
Если частные производные функцииz=f(x,y) существуют в некоторой
окрестности точки (x,y) и непрерывны
в самой точке (x,y), то функция
z=f(x,y) дифференцируема в этой точке.





 mathematics
mathematics








