Презентация Ремезов

1.

Бином Ньютона
Проект сделал учащийся 9 “Г” класса
Ремезов Георгий.

2.

Оглавление
1.
2.
3.
4.
5.
6.
7.
8.
9.
Что такое бином Ньютона?
Подробнее о биноме Ньютона
История создания
Подтверждения работоспособности бинома
Доказательство
Обобщение
Треугольник Паскаля
Заключение
Источники и литература

3.

Что такое бином Ньютона?
Бином Ньютона — формула для разложения на отдельные слагаемые целой
неотрицательной степени суммы двух переменных вида (a + b)ⁿ.

4.

Подробнее о биноме Ньютона
Обозначения:
C(n, k)
n
aиb
— Биномиальный коэффициент.
— Степень, в которую возводится двучлен.
— Переменные или числа.
В общем случае бином представляет собой бесконечный ряд.

5.

История создания
Долгое время считалось, что для натуральных показателей степени эту формулу, как и
треугольник, позволяющий находить коэффициенты, изобрел Блез Паскаль,
описавший её в XVII веке. Однако историки науки обнаружили, что формула была
известна ещё китайскому математику Яну Хуэю, жившему в XIII веке, а также
персидским математикам ат-Туси (XIII век) и аль-Каши (XV век).
Исаак Ньютон около 1665 года обобщил формулу для произвольного показателя
степени (дробного, отрицательного и др.). На основе биномиального разложения
Ньютон, а позднее Эйлер, выводили всю теорию бесконечных рядов.

6.

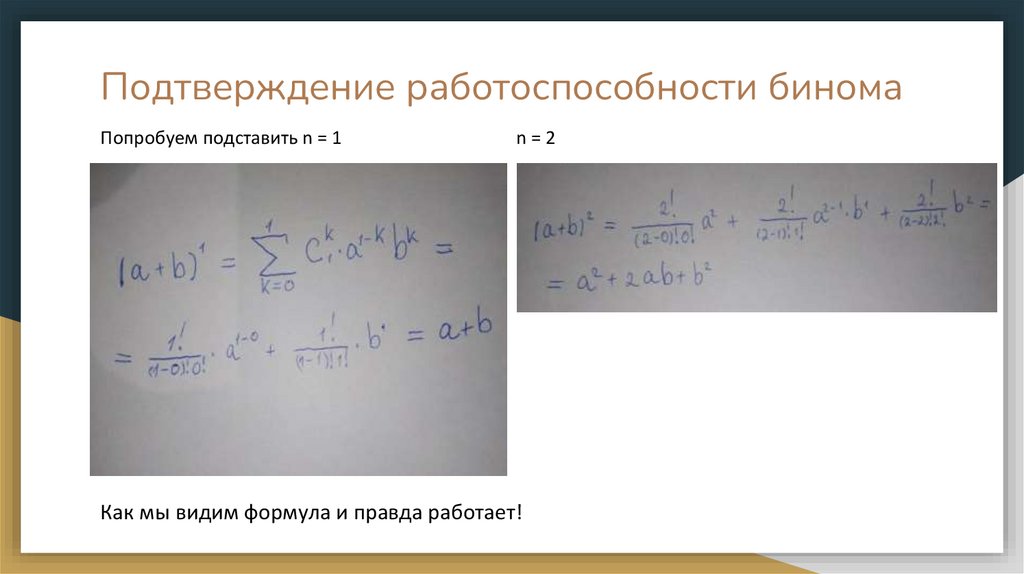
Подтверждение работоспособности бинома
Попробуем подставить n = 1
n=2
Как мы видим формула и правда работает!

7.

Доказательство
Чтобы умножить скобки, нужно взять из каждой по одному слагаемому и все
полученные произведения сложить.
Для получения степени a^k * b ^ (n−k)
нужно из k скобок выбрать a, а из оставшихся n−k выбрать b.
Вариантов выбрать a в первый раз столько же, сколько и скобок, то есть n. Затем,
соответственно, n−1, и так далее до n−k+1 на k-м шаге.
Однако для каждого варианта посчитаются и все его порядковые перестановки, число
которых k!.
Формируя, получаем в точности C(n, k).

8.

Обобщения
Формула бинома Ньютона является частным случаем разложения функции (1+x)^r в
ряд Тейлора:
Где r может быть произвольным комплексным числом (в частности, отрицательным или
вещественным). Коэффициенты этого разложения находятся по формуле

9.

Треугольник Паскаля
Мы можем использовать треугольник Паскаля для разложения бинома формы (a +
b)^n гораздо более простым способом.

10.

Заключение
Биномиальная теорема является одним из ключевых результатов алгебры,
открывающим широкий спектр применения в различных областях математики,
включая комбинаторику, теорию вероятностей и финансовую математику.
Благодаря возможности разложения каждой степени суммы (a + b)^n на
составляющие с использованием биномиальных коэффициентов, мы получаем
мощный инструмент для анализа и обработки многочленов.

11.

Источники и литература
https://docs.google.com/presentation/ - Google Презентации
https://www.wikipedia.org/ - Электронная энциклопедия
https://studfile.net/ - Каталог с изображениями