6. Методика изучения арифметических действий

1.

Методика изучения
арифметических действий
Лектор: Фатихова Лидия Фаварисовна, к.п.н., доцент
кафедры специальной педагогики и психологии БГПУ
им. М. Акмуллы

2.

План лекции:
1. Общая характеристика вычислительных приемов.
2. Методика формирование вычислительных приемов.
2.1. Обучение сложению и вычитанию в пределах 10.
2.2. Обучение сложению и вычитанию в пределах 20.
2.3. Обучение сложению и вычитанию в пределах 100.
Изучение табличного умножения и деления.
2.4. Изучение арифметических действий в пределах
1000.
2.5. Изучение арифметических действий с
многозначными числами.

3.

1.
Общая характеристика
приемов
вычислительных
Вычислительный навык – это высокая степень
овладения вычислительным приемом. Приобрести
вычислительный навык – это значит для каждого случая
знать, какие операции и в каком порядке следует
выполнять, чтобы найти результат арифметического
действия, и выполнять эти операции достаточно
быстро.
Наибольшая автоматизация выполнения действия
должна достигаться в следующих случаях:
1) табличные случаи сложения и вычитания в пределах
10-ти и 20-ти;
2) табличные случаи умножения и соответствующие
случаи деления.

4.

Классификация вычислительных приемов (навыков) в
зависимости от их теоретической основы
(по М.А. Бантовой)
Группа
Теоретическая
основа
Пример
1
конкретный
смысл
арифметически
х действий
1) а + 2, 3, 4, 0; а - 2, 3, 4, 0 (сложение и
вычитание в пределах 10-ти);
2) 9 + 5, 12 – 5 (сложение и вычитание с
переходом через десяток);
3) табличные случаи умножения;
4) табличные случаи деления (на начальном
этапе);
5) 1 · а, 0 · а.
2
свойства
арифметически
х действий
1) 2 + 8 (переместительное свойство сложения);
2) 14 · 5 (свойство умножения суммы на число);
3) 5 · 14 (переместительное свойство
умножения);
4) 81 : 3 (свойство деления суммы на число);
5) 18 · 40 (свойство умножения числа на
произведения).

5.

Группа
Теоретическая
основа
Пример
3
связи между
9 – 7, 24 : 6 , 60 : 20, 54 : 18, 9: 1, 0 : 6
компонентами и
результатами
арифметически
х действий
4
правила
1) а · 0, а · 1 (правила умножения на 0 и 1);
2) 34 + 20, 34 + 2 (правило: десятки складывают
с десятками, единицы с единицами)
5
вопросы
нумерации
чисел
а + 1, а – 1, 10 + 6, 16 – 6, 16 – 10, 57 · 10,
1200 : 100
6
изменение
1) 46 + 19 (прием округления: округляем 19 до
результатов в
20-ти, 46+ 20 = 66; если мы увеличили
зависимости от
слагаемое на 1, то сумму нужно уменьшить на
изменения
1: 66 – 1 = 65);
одного из
2) приемы умножения и деления на 5, 25, 50
компонентов

6.

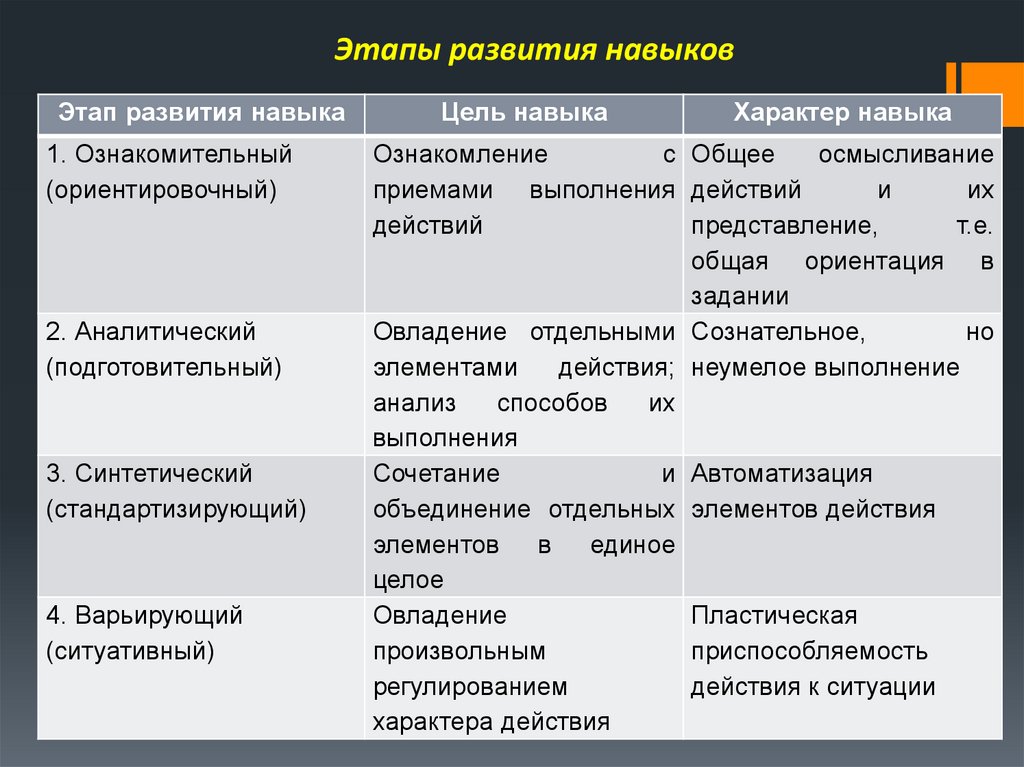
Этапы развития навыков
Этап развития навыка
1. Ознакомительный
(ориентировочный)
2. Аналитический
(подготовительный)
3. Синтетический
(стандартизирующий)
4. Варьирующий
(ситуативный)
Цель навыка
Характер навыка
Ознакомление
с Общее
осмысливание
приемами выполнения действий
и
их
действий
представление,
т.е.
общая ориентация в
задании
Овладение отдельными Сознательное,
но
элементами
действия; неумелое выполнение
анализ
способов
их
выполнения
Сочетание
и Автоматизация
объединение отдельных элементов действия
элементов в единое
целое
Овладение
Пластическая
произвольным
приспособляемость
регулированием
действия к ситуации
характера действия

7.

Сопоставление этапов развития навыка с этапами
формирования вычислительного навыка,
выделенными М.А. Бантовой
Этап
формирования ВН
1. Закрепление
знания
вычислительного
приема
2. Частичное
свертывание
выполнения
операций
Психологический
Характеристика этапа
этап развития
навыка
Учащиеся
самостоятельно Аналитический
выполняют
все
операции,
комментируя выполнение каждой из
них
вслух
и
одновременно
производя развернутую
запись,
если она была предусмотрена.
Происходит
свертывание Начало
вспомогательных
операций. синтетического
Учащиеся про себя выделяют этапа
операции и обосновывают выбор и
порядок их выполнения, вслух же
они проговаривают выполнение
основных
операций,
т.е.
промежуточных вычислений

8.

Этап
формирования
ВН
3. Полное
свертывание
выполнения
операций
4. Предельное
свертывание
выполнения
операций
Психологический
Характеристика этапа
этап развития
навыка
Происходит свертывание не только Синтетический
вспомогательных, но и основных
операций.
Учащиеся
про
себя
выполняют все операции, называют и
записывают
только
окончательный
результат.
Свертывание
основных
операций
несколько
отстает
от
свертывания
вспомогательных
операций, благодаря чему основные
операции будут актуализироваться,
Актуализация основных операций и
выполнение их в свернутом плане и
есть
собственно
вычислительный
навык.
Учащиеся выполняют все операции в Варьирующий
свернутом плане, предельно быстро,
т.е. они овладевают вычислительным
навыком. Навык может использоваться
в любых ситуациях, при варьировании
условий его применения.

9.

2. Методика формирования вычислительных
приемов
2.1. Обучение сложению и вычитанию в пределах 10.
С арифметическими действиями учащиеся знакомятся сразу
же после изучения числа 2. Изучение каждого из чисел
первого десятка (кроме 1), завершается изучением действий
сложения и вычитания в пределах этого числа. Действие
сложение и вычитание изучаются параллельно.
Основные задачи:
1) обеспечить усвоение детьми рациональных
вычислительных приемов сложения и вычитания в
пределах первого десятка;
2) сформировать правильные вычислительные навыки;
3) добиться запоминания наизусть результатов сложения и
вычитания, а также состава чисел первого десятка.

10.

Знания, умения и навыки при овладении сложением
вычитанием в пределах 10:
1) знакомство со знаками сложения - плюсом (+),
вычитания – минусом (-) и знаком равенства – равно
(=);
2) умение присчитывать и отсчитывать по 1;
3) умение отсчитывать (вычитать) по 1;
4) овладение приемами вычисления, формирование
прочных вычислительных навыков;
5) заучивание результатов сложения и вычитания в
пределах 10 и состава чисел первого 10;
6) узнавание и показ компонентов и результатов двух
арифметических действий и понимание их названий в
речи учителя;
7) знакомство с приемами сложения и вычитания,
опирающимся на свойство натурального ряда чисел.

11.

Трудности учащихся при овладении сложением и
вычитанием в пределах 10:
1) трудности овладения приемом отсчитывания, который
основан на хорошем знании обратного счета, а
обратный счет для многих учащихся первого класса
труден;
2) плохое запоминание того, сколько нужно отнять,
сколько уже отняли, сколько ещё надо отнять.

12.

Этапы изучения сложения и вычитания в пределах 10:
1. Подготовительный этап: раскрывается смысл действия
сложения вычитания, запись и чтения примеров, случаи
прибавления и вычитания 1, где результаты образуются на
основе знания образования натуральной
последовательности чисел.
2. Изучения приемов присчитывания и отсчитывания по
одному и группами для случаев прибавить и вычесть 2, 3,
4.
3. Изучение приемов перестановки слагаемых для случаев:
прибавить 5, 6, 7, 8, 9. Усвоение таблицы сложения и
состава чисел из слагаемых.
4. Изучения приема вычитания на основе связи сложения и
вычитания для случаев вычитания 5, 6, 7, 8, 9.
5. При изучении каждого числа первого десятка учащиеся
получают представление и о составе этих чисел.

13.

Последовательность работы над вычислительными
навыками в пределах 10:
1) знакомство с приемами сложения и вычитания;
2) упражнения в применении этих приемов;
3) составление таблиц и заучивание их, овладение
вычислительными навыками.
Пример составленной таблицы на овладение вычислительным
навыком «прибавить и вычесть 2»
1+2=3
2+2=4
3+2=5
4+2=6
5+2=7
6+2=8
7+2=9
8+2=10
3-2=1
4-2=2
5-2=3
6-2=4
7-2=5
8-2=6
9-2=7
10-2=8

14.

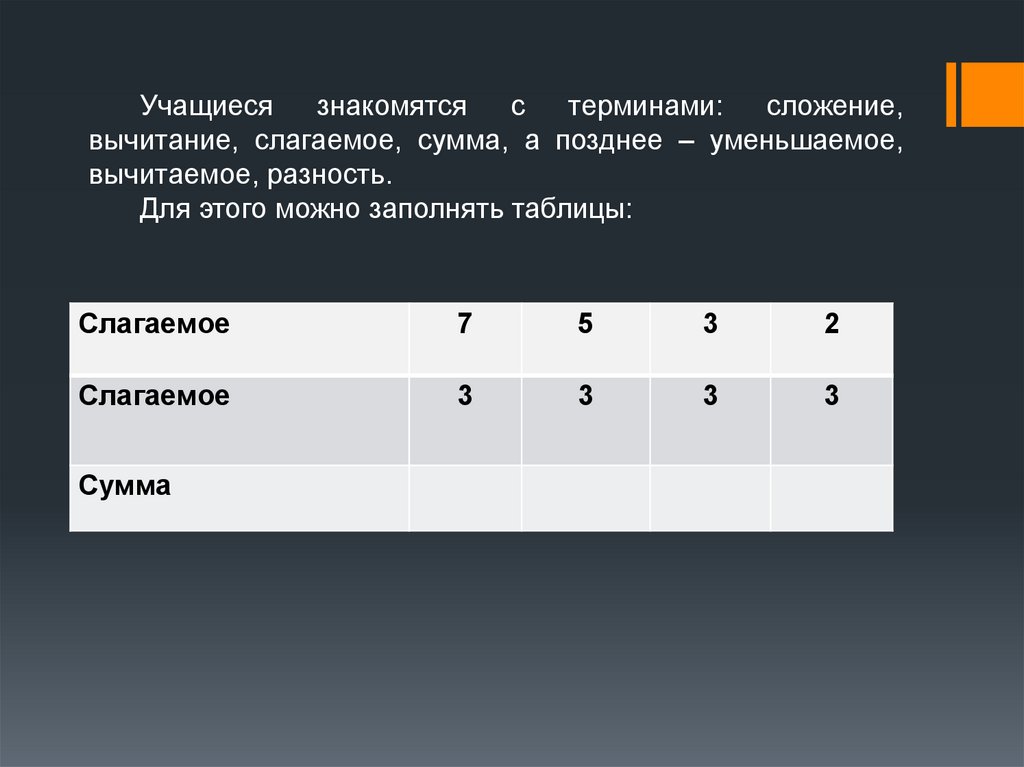
Учащиеся
знакомятся
с
терминами:
сложение,
вычитание, слагаемое, сумма, а позднее – уменьшаемое,
вычитаемое, разность.
Для этого можно заполнять таблицы:
Слагаемое
7
5
3
2
Слагаемое
3
3
3
3
Сумма

15.

В процессе изучения сложения и вычитания продолжается
формирование понятия о числе нуль. Нуль сравнивается с
единицей. Устанавливается, что ноль меньше единицы,
единица больше нуля, поэтому ноль должен стоять перед
единицей. Однако учитель должен помнить, что ноль не
относится к натуральным числам. Поэтому ряд натуральных
чисел должен начинаться с единицы.
Этапы работы изучения сложения в процессе
формирования понятия о нуле:
1) используются случаи вычитания, когда вычитаемое равно
уменьшаемому, чтобы в результате получился 0 (2-2, 3-3 и
т.д.). При этом опираются на решение соответствующих
задач;
2) в конце изучения темы «Десяток» включают случаи сложения
и вычитания с нулем (8+0, 6-0 и др.) с использованием
иллюстраций.

16.

2.2. Обучение сложению и вычитанию в пределах 20.
Овладение вычислительными приемами сложения и вычитания в
пределах 20 основано на хорошем знании сложения и вычитания
в пределах 10, знании нумерации и состава чисел в пределах 20.
При этом используются все виды наглядных пособий,
используемых при изучении нумерации, используются и при
изучении арифметических действий.
Во втором классе учащиеся должны знать:
1. Название компонентов действий сложения и вычитания.
2. Приемы сложения и вычитания, основанные на знаниях
десятичного состава чисел.
3. Сложение и вычитание без перехода через десяток:
а) к двухзначному числу прибавляется однозначное число. Из
двухзначного числа вычитается однозначное число;
б) получение суммы 20 и вычитание однозначного числа из 20;
в) вычитание из двухзначного числа двухзначного: 15-12, 20-15.

17.

Решение примеров с переходом через десяток можно
объяснить разными приемами:
1) разложить уменьшаемое и вычитаемое на десятки и
единицы и вычитать десятки из десятков, единицы из
единиц;
2) разложить вычитаемое на десяток и единицы. Вычитать из
уменьшаемого десятки, а из полученного числа – единицы;
3) сложение и вычитание с переходом через ряд
представляет наибольшие трудности для учащихся с
психофизическими нарушениями.

18.

Вычитание с переходом через десяток требует
ряд операций:
1) уменьшаемое разложить на десяток и единицы;
2) вычитаемое разложить на два числа, одно из которых
равно числу уменьшаемого единицы;
3) вычесть единицы;
4) вычесть из десятка оставшееся число единиц.

19.

Подготовительная работа должна заключаться в
повторении:
а) таблицы сложения и вычитания в пределах 10;
б) состава чисел первого десятка (всех возможных
вариантов из двух чисел);
в) дополнения чисел до 10;
г) разложения двухзначного числа на десятки и единицы;
д) вычитания из десяти однозначных чисел;
е) рассмотрения случаев вида 17-7, 15-5.

20.

2.3. Обучение сложению и вычитанию в пределах
100. Изучение табличного умножения и деления.
Основные задачи обучения сложению и вычитанию в
пределах 100:
1) знакомство с вычислительными приемами и
формирование умения применять их при сложении и
вычитании в пределах 100;
2) закрепление навыков табличного сложения и вычитания
в пределах 10;
3) формирование навыков табличного сложения чисел в
пределах 20;
4) усвоение связи между компонентами и результатом
действий вычитания.

21.

Обучение сложению и вычитанию в пределах 100
При обучении сложению и вычитанию в пределах 100
соблюдаются все требования, которые
предъявляются к обучению выполнению действий в
пределах 20. Многие трудности, которые испытывают
дети при выполнении действий сложения и вычитания
в пределах 20, не снимаются и при выполнении этих
же действий в пределах 100. По-прежнему большие
затруднения учащиеся испытывают при выполнении
действия вычитания. Наибольшее количество ошибок
возникает при решении примеров на сложение и
вычитание: из единиц вычитаемого единицы
уменьшаемого.

22.

Последовательность изучения действий
сложения и вычитания в пределах 100:
1. Сложение и вычитание круглых десятков (30 + 20, 50-20,
решение основано на знании нумерации круглых
десятков)
2. Сложение и вычитание без перехода через разряд.
3. Сложение двухзначного числа с однозначным числом,
когда в сумме получается круглые десятки. Вычитание из
круглых десятков однозначного и двухзначного числа.
4. Сложение и вычитание с переходом через разряд.
Примечание: все действия с примерами 1, 2 групп
выполняются приемами устных вычислений, то есть
вычисления надо начинать с единиц высших разрядов.
Запись примеров производится в нумерации,
десятичного состава чисел, таблиц сложения и
вычитания в пределах 10. Действия сложения и
вычитания изучаются параллельно.

23.

Система обучения умножению и делению в
пределах 100:
1. Введение понятия об умножении как сумм одинаковых
слагаемых.
2. Составление таблицы умножения числа 2.
3. Понятие деления на равные части.
4. Составление таблицы деления на 2.
5. Составление таблицы умножения в пределах 20.
6. Составление таблицы деления в пределах 20.
7. Деление по содержанию.
8. Сопоставление умножения и деления как
взаимообратных действий.
9. Изучение умножения в пределах 100. Составление
таблиц умножения и деления. Практическое знакомство
с переместительным законом умножения.
10. Деление с остатками.
11. Умножение на 1 и единицы. Деление на 1. Ноль как
компонент умножения. Ноль как делимое.

24.

Обучение табличному умножению и делению в
пределах 20
В 2 классе учащиеся получают понятие об умножении и
знакомятся с действиями умножения и деления в пределах 20.
Лучшему осознанию учащимся смысла действия умножения
способствует подготовительная работа: счет равными группами
предметов, а также счет по 2, 3, 4, 5, до 20.
После того как учащиеся получают первое представление об
умножении, познакомятся со знаком умножения и записью этого
действия, можно переходить к изучению таблицы умножения
числа 2.
Таблица умножения составляется по постоянному множимому.
Этапы знакомства с табличным умножением числа 2:
1.
2.
3.
Счет предметов от 2 до 20.
Счет изображений предметов по 2 на рисунках или числовых
фигурках и составление примеров на сложение.
Замена сложения умножением и чтения таблицы умножения.

25.

Обучение табличному делению в пределах 20
В начальных классах действие деления рассматривается в
зависимости от действия умножения. Только тогда дети хорошо
усваивают сущность деления, когда сопоставляется с
умножением, устанавливается взаимосвязь между этими двумя
действиями. Опыт показывает, что вывод деления из умножения
без объявления сущности самого процесса деления оказывается
малопонятным.
Деление с остатком вводится после изучения табличного деления.
На деление с остатком дети допускают много ошибок. Они либо
не записывают, либо прибавляют его к частному, либо получают
остаток больше делителя.
Во 2 классе повторяется табличное умножение в пределах 20 и
заканчивается изучение всего табличного умножения и деления.
По-прежнему много внимания уделяется наглядной основе и
счета равными группами их числам.
После составления таблицы умножения числа 6 учитель должен
обратить внимание на то, что ответ каждого последующего
примера может быть получен из предыдущего путем
прибавления 6 (единиц множимого).

26.

Внетабличное умножение и деление
Порядок изучения внетабличного умножения и
деления:
1) рассматриваются правила умножения числа на
сумму и суммы на число;
2) изучается умножение и деление чисел,
оканчивающихся нулем, вводится умножение
двухзначного числа на однозначное и умножение
однозначного числа на двухзначное;
3) вводится правило деления суммы на число, на
основе которого раскрывается прием деления
двухзначного числа на однозначное;
4) рассматривается деление двухзначного числа на
двухзначное, вводится проверка умножения и
деления.

27.

1. Приемы (способы) умножения числа на
сумму:
4*(3+2)
• 4*(3+2)=4*5=20
• 4*(3+2)=4*3+4*2=20
Аналогичным способом изучаются умножение
суммы на число и деление суммы на число.
Приемы для случаев умножения и деления чисел,
оканчивающихся нулем:
Умножение
20*3
2 дес.*3=6 дес.
20*3=60
Деление
80:4
8 дес.:4=2 дес.
80*2=20

28.

2. Умножение однозначных чисел на круглые
двухзначные
Используется прием перестановки множителей:
(4*20=20*4).
Деление двухзначных чисел на круглые двухзначные
выполняется способом подбора частного на основе
связи между компонентами и результатом умножения.
Например:
60:20 – надо подобрать такое число, при умножении
которого на 20 получится 60. 2 не подходит, 3
подходит, т.к. 20, т.к. 20*3=60, значит, 60:20=3.

29.

3. Умножение двухзначного числа на однозначное и
умножение однозначного на двухзначное
Прием умножения двухзначного числа на однозначное учащиеся
могут применять самостоятельно, объясняя ход решения по
развернутой записи:
12*3=(10+2)*3=10*3+2*3=36
При умножении однозначного числа на двухзначное используются:
1) правило умножения числа на сумму:
6*12=6*(10+2)=6*10+6*2=72;
2) переместительное свойство умножения: 6*12=12*6=72.
При делении двухзначного числа на однозначное используют
правило деления суммы на число. Используется следующая
последовательность изучения:
1) примеры, при решении которых приходится делимое заменять
суммой разрядных слагаемых: 36:3=(30+6):3=30:3+6:3=12;
2) примеры, при решении которых приходиться делимое заменять
суммой удобных слагаемых:
30:2=(20+10):2=20:2+10:2=15
78:6=(60+18):6=60:6+18:6=13

30.

4. Деление двухзначного числа на двухзначное
Используется способ подбора частного, который основан
на связи между компонентами и результатами действия
умножения: подбирают частное, а затем проверяют его
умножением:
81:27 (Какое число нужно умножить на 27, чтобы
получить 81? На число 3. Значит 81:27+27).

31.

Деление с остатком
Тема изучается в 3 классе после завершения работы над
внетабличным умножением и делением. При делении с остатком по
двум данным числам – делимому и делителю находят 2 числа:
частное и остаток.
Этапы изучения темы
1. В период подготовки к изучению темы решаются жизненно
практические задачи, когда дети складывают и раскладывают
предметы, устно отвечают на вопросы, проводится работа с
дидактическим материалом и с рисунками.
Пример:
Мама принесла 11 яблок и раздала детям, по 2 яблока каждому.
Сколько детей получили эти яблоки и сколько яблок осталось?
Решение задачи и запись:
11:2=5 (ост. 1).
Ответ: 5 детей и остается 1 яблоко.
2. Раскрывается соотношение между делителем и остатком, т.е.
ученики устанавливают: если пи делении получается остаток, то
он всегда меньше делителя. Для этого решаются примеры.
3. Проводятся упражнения на формирования данного
вычислительного навыка.

32.

2.4. Изучение арифметических действий в
пределах 1000.
Все действия в пределах 1000 без перехода через разряд
учащиеся выполняют приемами устных вычислений с
записью в строчку, а с переходом через разряд – приемами
письменных вычислений с записью в столбик. Важно
постепенно
нарастание
трудности
при
решении
арифметических примеров, каждый последующий уровень
в решении примеров должен опираться на знание
предыдущих случаев. Непреодолимые трудности для
ребенка могут возникнуть при несоблюдении степени
трудности решения примеров. Поэтому очень важно
соблюдать последовательность в выборе примеров,
учитывая их нарастающую степень трудности, и тщательно
отрабатывать каждый случай.

33.

Сложение и вычитание в пределах 1000
№
Этап
Задачи
1
Сложение и
вычитание без
перехода через
разряд
1) сложение и вычитание круглых сотен. Действие
производится на основе знаний нумерации, и
сводятся по существу к действиям в пределах 10
2) сложение и вычитание круглых сотен и единиц,
круглых сотен и десятков
3) сложение и вычитание круглых десятков, а также
круглых сотен десяток
4) сложение трехзначных чисел с однозначным
числом, двухзначным и трехзначным без
перехода через разряд и соответствующие случаи
вычитания
5) особые случаи сложения и вычитания. К ним
относятся случаи, которые вызывают наибольшие
трудности и в которых чаще всего допускают
ошибки. Учащихся больше всего затрудняют
действия с нулем, (ноль находится в середине
или в конце)

34.

№
2
Этап
Сложение и
вычитание с
переходом
через разряд
Задачи
1) сложение и вычитание с переходом через разряд
в одном разряде (единиц или десятков)
2) сложение и вычитание с переходом через разряд
в двух разрядах (единиц или десятков)
3) особые случаи сложения и вычитания, когда в
сумме или разности получается один или два
нуля, когда в уменьшаемом содержится один или
два нуля, когда в уменьшаемом содержится
единица
4) вычитание трехзначных, двухзначных и
однозначных чисел из 1000

35.

Умножение и деление в пределах 1000
№
Этап
1
Устное
умножение и
деление в
пределах 1000
Задачи
1) умножение и деление круглых сотен
2) умножение и деление круглых десятков на
однозначное число:
а) рассматриваются случаи умножения и деления
круглых десятков, которые сводятся к табличному
умножению и делению;
б) рассматриваются случаи, которые сводятся к
нетабличному умножению и делению без перехода
через разряд.
2
Умножение и деление трехзначных чисел на однозначное число без
перехода через разряд
3
Умножение десяти и ста, умножение на 10 и 100

36.

№
Этап
Задачи
4
Деление на
10 и 100
1) письменное умножение и деление в пределах 1000
2) умножение и деление на однозначное число с
переходом через разряд
3) умножение двухзначного числа на однозначное с
переходом через разряд в разряде десятков или
единиц
4) умножение двухзначного числа на однозначное с
переходом через разряд в разряде единиц и
десятков
5) умножение трехзначного числа на однозначное
число с переходом через разряд в одном разряде единиц или десятков
6) умножение трехзначного числа на однозначное
число с переходом через разряд в двух разрядах единиц и десятков
7) особый случай умножения - первый множитель трехзначное число с нулем на конце или в середине
8) умножение двухзначного числа на круглые десятки

37.

Деление изучается в последовательности:
1. Число сотен, десятков и единиц делится без остатка на
делитель.
2. Число сотен делится на делитель без остатка, а число
десятков без остатка на делитель не делится.
3. Число сотен не делится без остатка на делитель.
4. Число сотен делимого меньше числа единиц делителя, в
частном получается двухзначное число.
5. Особый случай деления, когда в частном на конце или в
середине получается ноль.
6. Деление на круглые десятки.

38.

2.5. Изучение арифметических действий с
многозначными числами.
Сложение и вычитание многозначных чисел
выполняются преимущественно приемами
письменных вычислений. Основой алгоритмов
сложения и вычитания чисел любого класса
является поразрядное сложение и вычитание.

39.

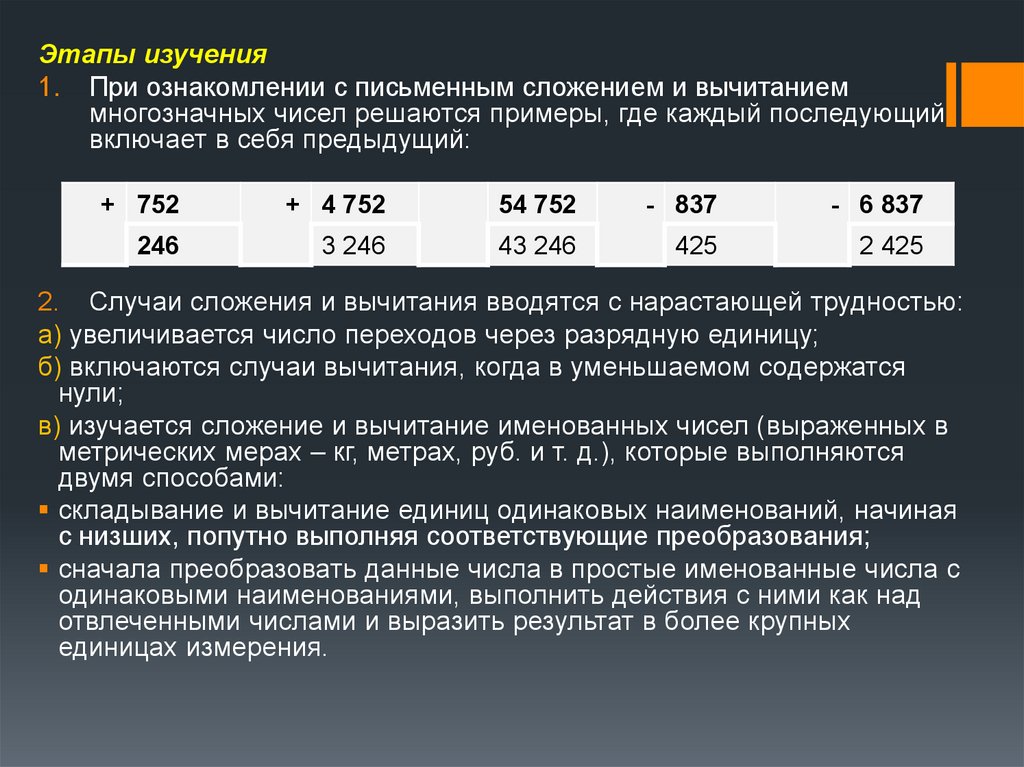
Этапы изучения
1. При ознакомлении с письменным сложением и вычитанием
многозначных чисел решаются примеры, где каждый последующий
включает в себя предыдущий:
+ 752
+ 4 752
54 752
- 837
- 6 837
246
3 246
43 246
425
2 425
2. Случаи сложения и вычитания вводятся с нарастающей трудностью:
а) увеличивается число переходов через разрядную единицу;
б) включаются случаи вычитания, когда в уменьшаемом содержатся
нули;
в) изучается сложение и вычитание именованных чисел (выраженных в
метрических мерах – кг, метрах, руб. и т. д.), которые выполняются
двумя способами:
складывание и вычитание единиц одинаковых наименований, начиная
с низших, попутно выполняя соответствующие преобразования;
сначала преобразовать данные числа в простые именованные числа с
одинаковыми наименованиями, выполнить действия с ними как над
отвлеченными числами и выразить результат в более крупных
единицах измерения.

40.

Умножение и деление многозначных чисел
Умножение и деление многозначных чисел представляет гораздо
больше трудностей, чем сложение и вычитание, т.к. учащиеся не
твердо знают таблицу умножения. Трудности возникают и тогда,
когда надо единицы высшего разряда перевести в низший
разряд, удержать их в памяти. Неумение долгое время
сосредоточить внимание на выполнение действия приводит к
тому, что учащиеся низшие разряды числа умножают правильно,
а при умножении высших разрядов допускают ошибки.
Этапы умножение и деления многозначных чисел:
1) умножение и деление на однозначное число (1, 2, 3…9);
2) умножение и деление на разрядные числа (10, 100, 1000, 40,
4000…);
3) умножение и деление на двузначное и трехзначное число (12,
35…).
На каждом из данных этапов сначала изучается умножение, а
затем деление.

41.

Спасибо за внимание!