7. Методика обучения решению арифметических задач

1.

Методика обучения решению
арифметических задач
Лектор: Фатихова Лидия Фаварисовна, к.п.н., доцент
кафедры специальной педагогики и психологии БГПУ
им. М. Акмуллы

2.

План лекции:
1. Основные положения обучения решению
арифметических задач.
2. Методика обучения решения простых
арифметических задач:
3. Методика решения составных (сложных)
арифметических задач.

3.

1. Основные положения обучения решению
арифметических задач
Решение арифметических задач позволяет:
1)
2)
3)
4)
5)
6)
7)
раскрыть основной смысл арифметических действий,
конкретизировать их, связать с определенной жизненной ситуацией;
усваивать математические понятия, отношения, закономерности,
ознакомить с такими математическими отношениями, как
нахождение суммы и остатка (на сколько меньше, на сколько
больше, «больше на ...», «меньше на ...», «столько, сколько» и
другими);
развивать произвольное внимание, наблюдательность, логическое
мышление, речь, сообразительность.
развивать процессов познавательной деятельности: анализ, синтез,
сравнение, обобщение.
обучать учащихся планировать и контролировать свою
деятельность, овладевать приёмами, самоконтроля (проверка
задачи прикидка задач и т.д.)
воспитывать настойчивость, волю, интерес к поиску решения задачи.
обучать переводу отношений между предметами и величинами на
«язык математики».

4.

Арифметическая задача – это словесная модель
ситуации, явления, события, процесса. Под
моделированием задачи понимается замена действий с
обычными предметами, действиями с их моделями —
уменьшенными образцами, муляжами, макетами, графами,
а также с их графическими изображениями, рисунками,
схемами, чертежами.
В арифметических задачах используется числовой
материал, отражающий успехи страны в различных
отраслях народного хозяйства, культуры, науки и т.д. Это
способствует расширению кругозора учащихся,
обогащению их новыми знаниями об окружающей
действительности. Умением решать арифметические
задачи учащиеся овладевают с большим трудом.

5.

Последовательность решения арифметической
(текстовой) задачи
1)
2)
3)
4)
5)
6)
чтение и осмысление текста задачи. При этом
предполагается, что ученики понимают значение каждого
слова в тексте задачи и мысленно представляют ситуацию,
изложенную в ней;
выявление в тексте задачи условия (известных и
неизвестных величин) и вопроса-требования;
установление связи между данными и между данными и
искомыми величинами (между условием и вопросом
задачи). На этой основе умение смоделировать отношения,
данные в задаче (перевести ее на язык математических
схем, символов и отношений);
составление плана решения задачи и выбор
арифметического действия для ее решения;
запись решения и ответа задачи;
работа над задачей после ее решения.

6.

Составные части задачи
1. Условие — то, что известно в задаче.
2. Вопрос — то, что надо узнать в задаче.
3. Решение — выполнение арифметических действий.
4. Ответ — результат полученного действия.

7.

Этапы решения задачи:
1. Ознакомление с содержанием задачи.
2. Поиск решения задачи предполагает отделение
вопроса задачи от условия, установление известных и
неизвестных величин и связи между ними.
3. Составление плана решения задачи и выбора
соответствующего арифметического действия.
4. Осуществление плана решения задачи – это
выполнение арифметических действий, выбранных
при составлении плана задачи.
5. Анализ решения задачи, заключающийся в работе над
задачей после ее решения.
6. Закрепление умений решать задачи.

8.

Ошибки, которые учащиеся допускают при решении
задач:
1. Привнесение лишнего вопроса и действия.
2. Исключение нужного вопроса и действия.
3. Несоответствие вопросов действия: правильно
поставленные вопросы и неправильный выбор действий
или, наоборот, правильный выбор действий и неверная
формулировка вопросов.
4. Случайный подбор чисел и действий.
5. Ошибки наименования величин при выполнении действий:
а) наименования не пишутся; б) наименования пишутся
ошибочно, вне предметного понимания содержания задачи;
в) наименования пишутся лишь при отдельных
компонентах.
6. Ошибки в вычислениях.
7. Неверная формулировка ответа задачи
(сформулированный ответ не соответствует вопросу, задачи
и т.д.).

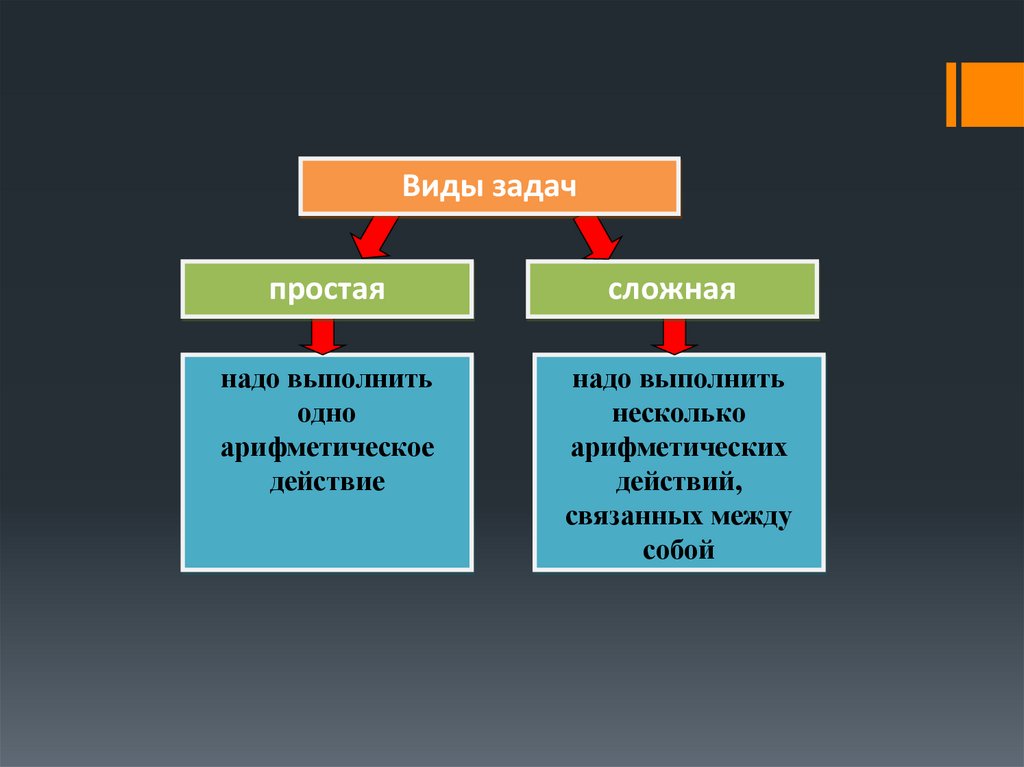
9.

Виды задач
простая
сложная
надо выполнить
одно
арифметическое
действие
надо выполнить
несколько
арифметических
действий,
связанных между
собой

10.

Виды простых и составных задач
1. Характеристика
Простые задачи на
Составные задачи
сложение и вычитание
Надо выполнить одно Включает в себя ряд
простых задач, связанных
арифметическое
действие.
Являются между
средством ознакомления собой так, что искомые
одних простых задач служат
с
математическими
данными других. Решение
отношениями: «больше задачи сводится к
на столько-то», «меньше расчленению ее на ряд
на столько-то», «столько- простых задач и
последовательному их
то», «столько, сколько»
решению.
и др.

11.

2. Виды
Простые задачи на
сложение и вычитание
Составные задачи
1.Задачи на нахождение суммы
чисел и остатка от числа –
решаются первыми и
раскрывают смысл
арифметического действия.
2.Задачи на увеличение
(уменьшение) числа на
несколько единиц.
3.Задачи на увеличение
(уменьшение) числа на
несколько единиц, одна из
исходных величин которых
выражена в косвенной
форме.
4.Задачи на нахождение
неизвестного слагаемого.
5.Задачи на разностное
сравнение чисел.
1. Задачи на разностное и кратное
сравнение.
2. Задачи на деление суммы на
число.
3. Задачи
на
нахождение
4-го
пропорционального.
4. Задачи
на
пропорциональное
деление.
5. Задачи на нахождение
неизвестного по двум разностям.
6. Задачи на движение в одном
направлении.
7. Задачи на встречное движение
двух тел.
8. Задача на движение двух тел в
противоположных направлениях.
9. Задачи на нахождение площади
фигур.
10. Задачи на нахождение периметра
геометрических фигур.
11. Задачи на нахождение числа по
доле и доли по числу.

12.

2.
Методика обучения
арифметических задач
решения
простых
Этапы работы над арифметической задачей:
1. Работа над содержанием задачи.
2. Поиск решения задачи.
3. Решение задачи.
4. Формулировка ответа.
5. Проверка решения задачи.
6. Последующая работа над решенной задачей.

13.

В процессе обучения решению арифметических задач
учитель задает специальные вопросы учащимся:
1. О чем эта задача, т.е. о каком процессе (явлении,
ситуации) идет речь в задаче, какими величинами
характеризуется этот процесс?
2. Что требуется найти в задаче?
3. Что обозначают те или иные слова в тексте задачи?
4. Что известно в задаче о названных величинах?
5. Что неизвестно?
6. Что является искомым?

14.

Большое внимание следует уделять работе над
содержанием задачи, т.е. над осмыслением ситуации
изложенной в задаче, установлением зависимости
между данными и искомым.
Последовательность работы над усвоением
содержания задачи:
1) разбор непонятных слов или выражений;
2) чтение текста задачи учителем и учащимся;
3) запись условия задачи;
4) повторение задачи по вопросам.

15.

Способы решения задач
Способ
Характеристика
Приемы решения
1. Арифметический
Ответ
находится 1) запись по действиям (с
посредством выполнения пояснением, без пояснения, с
арифметических
вопросами);
действий над числами.
2) запись в виде выражения.
2. Алгебраический
Ответ
находится
при 1) в виде
составлении и решении решения;
уравнения.
2) через
уравнения
и
его
запись
шагов
составления уравнения, самого
уравнения и его решения.

16.

Формы записи содержания задачи:
1. Сокращенная форма записи, при которой из текста задачи
выписывают числовые данные и только те слова и
выражения, которые необходимы для .понимания
логического смысла задачи.
2. Сокращенно-структурная форма записи, при которой
каждая логическая часть задачи записывается с новой
строки.
3. Схематическая форма записи.
4. Графическая форма записи.

17.

Приемы для включения контроля учащихся в
процесс решения задач:
1. Проверить словесно сформулированные задачи,
производя действие над предметами.
2. Проверять реальность ответа.
3. Проверять соответствие ответа условию и вопросу
задачи. Проверка решение задачи другим способам
её решения возможно с 4 класса.

18.

Приемы по закреплению решения задачи:
1. Ставятся узловые вопросы по содержанию задачи.
2. Предлагается рассказать весь ход решения задачи с
обоснованием выбора действий.
3. Ставятся вопросы к отдельным действиям или
вопросам.

19.

Значимость приема составления задач для
учащихся:
1) лучше осознают жизненно-практическую значимость
задачи, глубже понять её структуру;
2) различают задачи различных видов, осознают
приемы их решения.
Составление задач проводится параллельно с
решением готовых задач. Легче всего учащимся
составлять задачи частично. Очень полезно, когда
для составления задач учащиеся привлекают
материал «добываемый» ими во время экскурсий, из
справочников, газет, журналов и т.д.

20.

Подготовительный этап обучения решению
арифметических задач
1.
2.
3.
Учитель обогащает и развивает практический опыт учащихся, их
ориентировку в окружающей действительности. Учащиеся вводятся
в жизненную ситуацию, в которой придется решать арифметические
задачи, производить изменения.
Учитель организует наблюдение над изменением количества
элементов предметных множеств содержимого сосудов и т. д., что
способствует развитию представлений учащихся о количестве к
знакомству их с определенной терминологией, которая
впоследствии встретится при словесной формулировке задач:
стало, всего осталось, взяли, увеличилось, уменьшилось и т.д.
Организуется как игровая, так и практическая деятельность
учащихся: являясь непосредственными участниками этой
деятельности, а также наблюдая, учащиеся сами делают вывод в
каждом отдельном случае: увеличилось или уменьшилось число
элементов множества и какой операции и словесному выражению
соответствует это увеличение или уменьшение (этот этап совпадает
с началом работы над числами первого десятка и знакомства с
арифметическими действиями, с решением и составлением
примеров операций с предметными множествами).

21.

Этап обучения решения арифметических задач
1. Чтобы решить задачу, ученики должны решать
арифметические примеры, слушать, а затем читать задачу,
повторять задачу по вопросам, по краткой записи, по
памяти, выделять в задаче составные компоненты, решать
задачу и проверять ее правильность решения.
2. В 1 классе учащиеся учатся решать задачи на нахождение
суммы и остатка. Эти задачи вводятся впервые при
научении чисел первого десятка. При обучении решению
задач на нахождение суммы одинаковых слагаемых, на
деление на равные части или на деление по содержанию,
следует опираться на понимание учащимися сущности
арифметических действий умножения и деления.
3. До решения задачи на разностное сравнение чисел
учащимися нужно дать понятие о сравнение предметов
одной совокупности, двух предметных совокупностей,
величин, чисел, устанавливая между ними отношения
равенства и неравенства.

22.

3. Методика решения составных (сложных)
арифметических задач
Подготовительная работа к решению составных
задач
К решению составных задач учитель может переходить тогда,
когда учащиеся овладели приемами решения простых задач,
которые войдут в составную задачу, сами могут составить
простую задачу определенного вида. Проводится система
упражнений, приемов, целенаправленно ведущих учащихся к
овладению решением составных задач. При решении
составных задач учащиеся должны или к данным ставить
вопросы или к вопросу подбирать данные. Поэтому в
подготовительный период (в 1 классе и в начале 2 класса),
следует предлагать учащимся задания:
1. К готовому условию подобрать вопросы.
2. По вопросу составить задачу, подобрав недостающие
числовые данные.

23.

Общие приемы работы над задачей при обучении
учащихся решению сложных задач:
1) умение анализировать содержание задачи, выделяя
известные данные, искомое (т.е. устанавливая, что нужно
узнать в задаче);
2) Умение определять, каких данных не достает для ответа
на главный вопрос в задаче;
3) прием работы с карточками, заданиями в которых
излагается последовательность работы над задачей. При
решении задач оформление ее решения записывается с
вопросами или записывается каждое действие и
поясняется;
4) обобщенный способ решения сложных задач –
обеспечивается многократным решением задач с
разнообразными видами, решением готовых и
составленных самими учащимися задач, сравнением задач
данного вида с ранее решавшимися видами задач и т. д.

24.

Задачи, связанные с пропорциональными
величинами – это задачи на нахождение 4-го
пропорционального, на пропорциональное деление, на
нахождение неизвестных по двум разностям и задачи,
связанные с движением.

25.

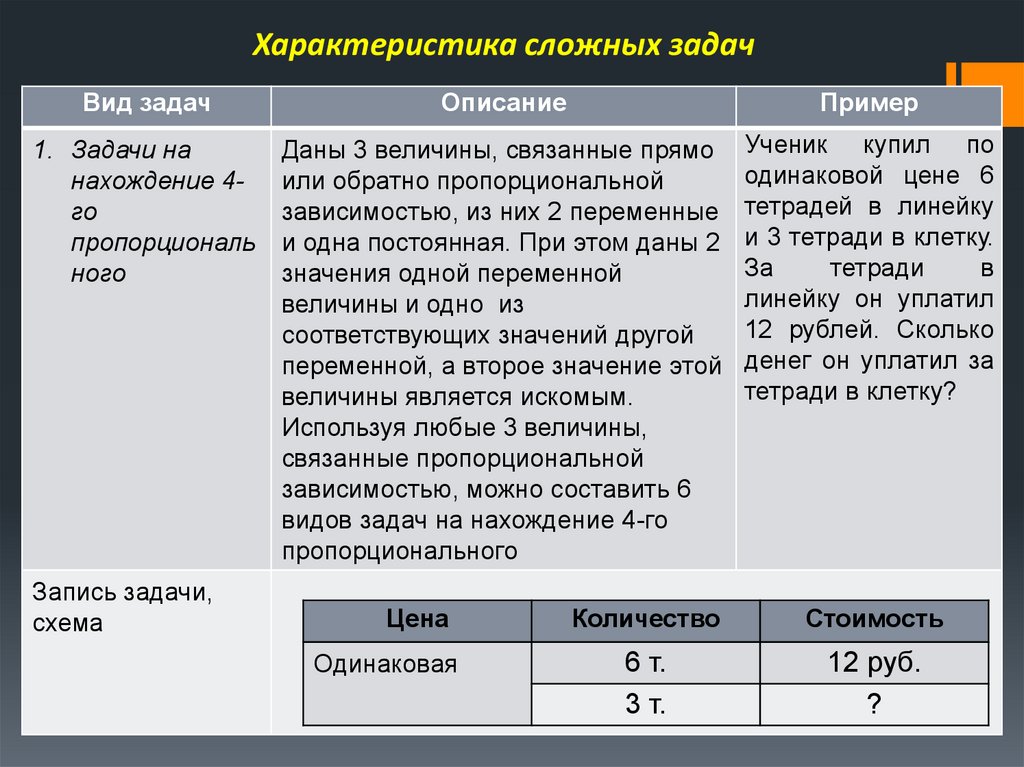
Характеристика сложных задач
Вид задач
Описание
Пример
1. Задачи на
нахождение 4го
пропорциональ
ного
Даны 3 величины, связанные прямо
или обратно пропорциональной
зависимостью, из них 2 переменные
и одна постоянная. При этом даны 2
значения одной переменной
величины и одно из
соответствующих значений другой
переменной, а второе значение этой
величины является искомым.
Используя любые 3 величины,
связанные пропорциональной
зависимостью, можно составить 6
видов задач на нахождение 4-го
пропорционального
Ученик купил по
одинаковой цене 6
тетрадей в линейку
и 3 тетради в клетку.
За
тетради
в
линейку он уплатил
12 рублей. Сколько
денег он уплатил за
тетради в клетку?
Запись задачи,
схема
Цена
Одинаковая
Количество
Стоимость
6 т.
3 т.
12 руб.
?

26.

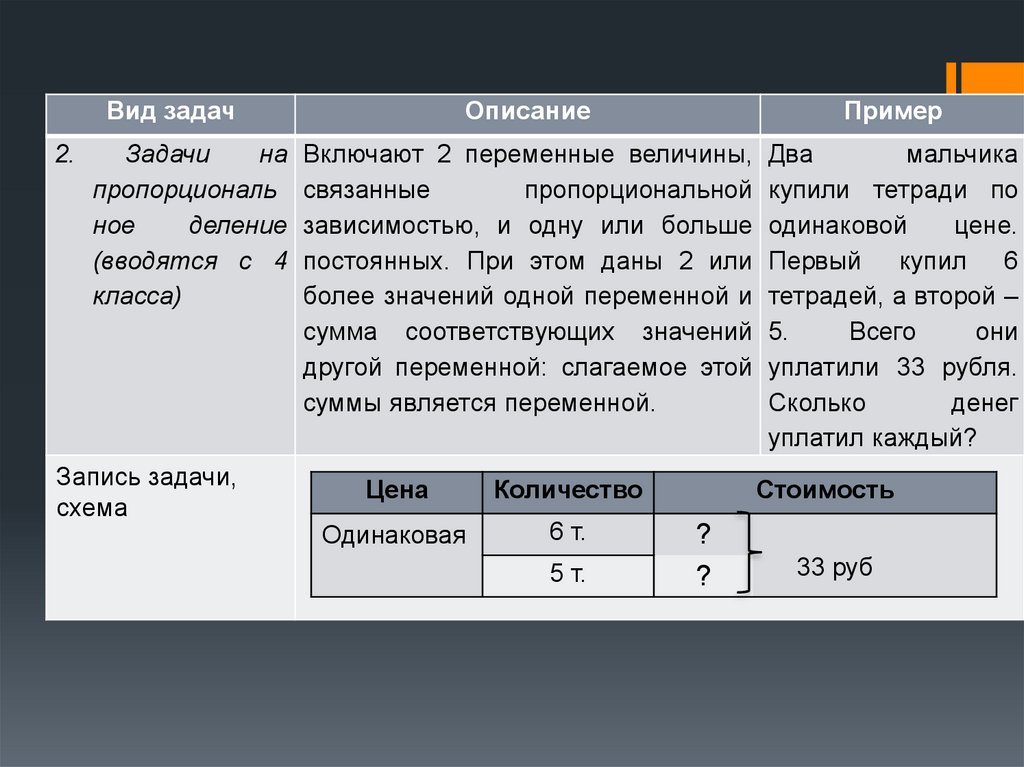
Вид задач
2.
Описание
Пример
Задачи
на Включают 2 переменные величины, Два
мальчика
пропорциональ связанные
пропорциональной купили тетради по
ное
деление зависимостью, и одну или больше одинаковой
цене.
(вводятся с 4 постоянных. При этом даны 2 или Первый купил 6
класса)
более значений одной переменной и тетрадей, а второй –
сумма соответствующих значений 5.
Всего
они
другой переменной: слагаемое этой уплатили 33 рубля.
суммы является переменной.
Сколько
денег
уплатил каждый?
Запись задачи,
схема
Цена
Количество
Одинаковая
6 т.
5 т.
Стоимость
?
?
33 руб

27.

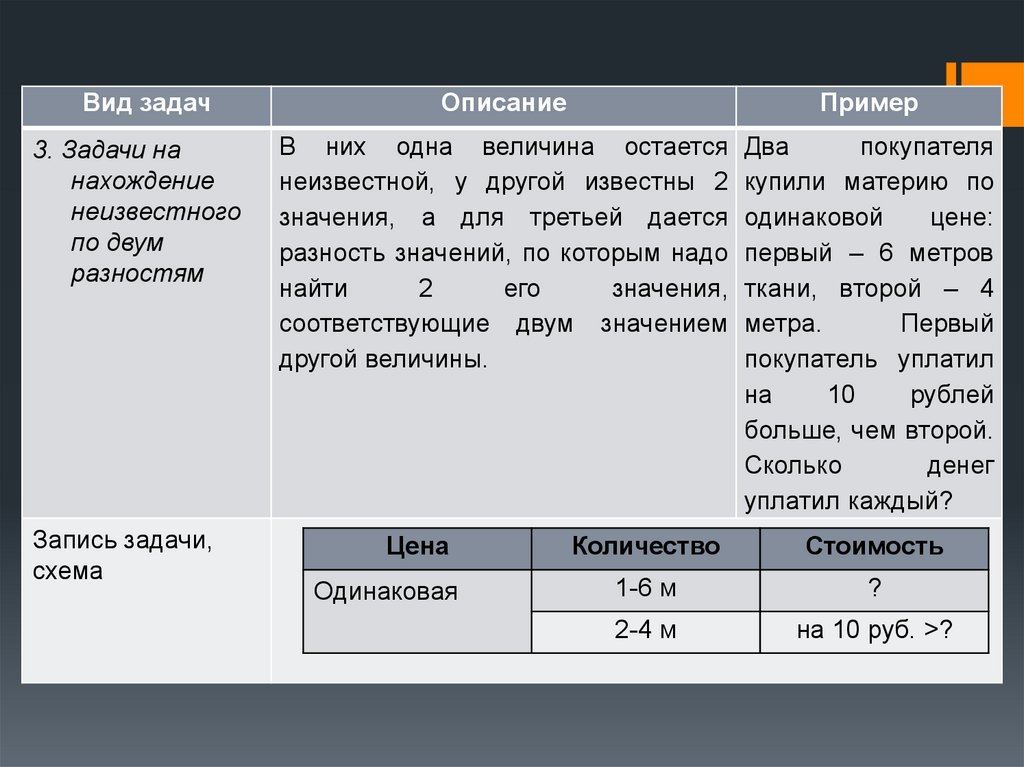
Вид задач
3. Задачи на
нахождение
неизвестного
по двум
разностям
Запись задачи,
схема
Описание
Пример
В них одна величина остается Два
покупателя
неизвестной, у другой известны 2 купили материю по
значения, а для третьей дается одинаковой
цене:
разность значений, по которым надо первый – 6 метров
найти
2
его
значения, ткани, второй – 4
соответствующие двум значением метра.
Первый
другой величины.
покупатель уплатил
на
10
рублей
больше, чем второй.
Сколько
денег
уплатил каждый?
Цена
Одинаковая
Количество
Стоимость
1-6 м
?
2-4 м
на 10 руб. >?

28.

Вид задач
4. Задачи,
связанные с
движением
(вводятся с 4
класса)
Описание
Пример
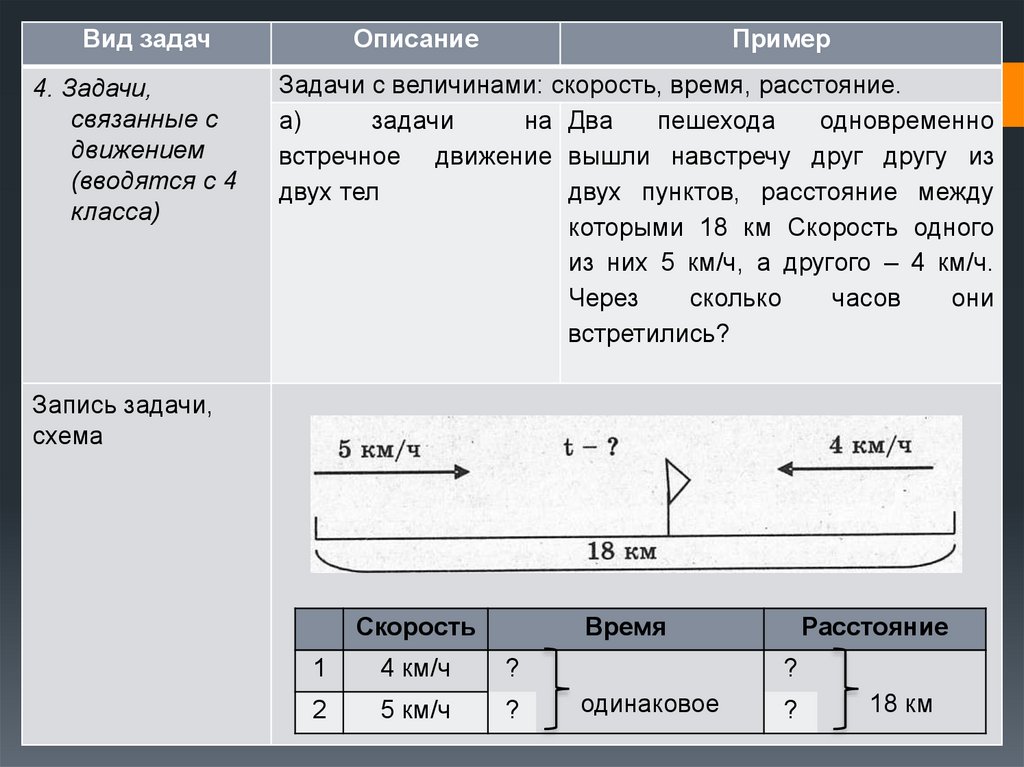
Задачи с величинами: скорость, время, расстояние.
а)
задачи
на Два
пешехода
одновременно
встречное движение вышли навстречу друг другу из
двух тел
двух пунктов, расстояние между
которыми 18 км Скорость одного
из них 5 км/ч, а другого – 4 км/ч.
Через
сколько
часов
они
встретились?
Запись задачи,
схема
Скорость
Время
1
4 км/ч
?
2
5 км/ч
?
Расстояние
?
одинаковое
?
18 км

29.

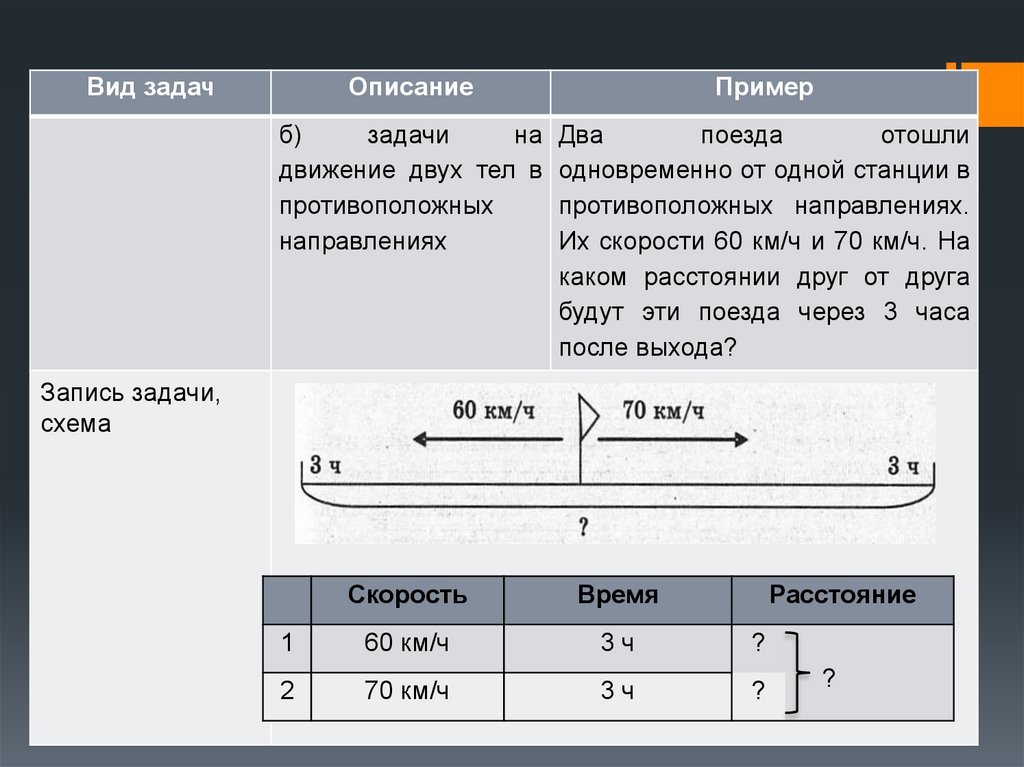
Вид задач
Описание
Пример
б)
задачи
на Два
поезда
отошли
движение двух тел в одновременно от одной станции в
противоположных
противоположных направлениях.
направлениях
Их скорости 60 км/ч и 70 км/ч. На
каком расстоянии друг от друга
будут эти поезда через 3 часа
после выхода?
Запись задачи,
схема
Скорость
Время
Расстояние
1
60 км/ч
3ч
?
2
70 км/ч
3ч
?
?

30.

Спасибо за внимание!