Методика обучения младших школьников решению задач

1.

2.

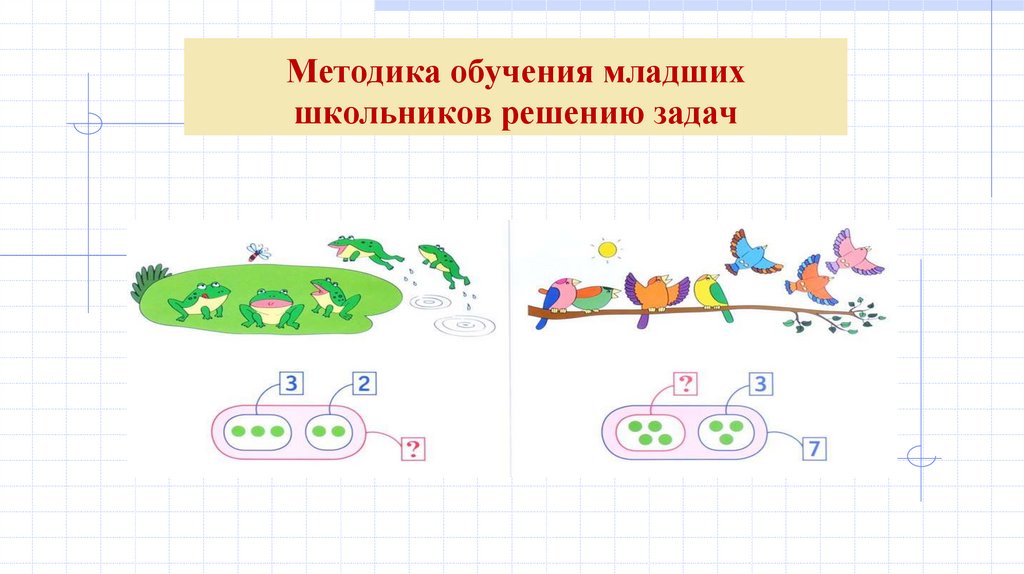
Методика обучения младших
школьников решению задач

3.

ЗАДАЧА:
Задача – это то, что требует разрешения,
исполнения (Ожегов С.И.).
Задача –
сформулированный словами вопрос,
ответ на который может быть получен с помощью
арифметических
действий
(Моро
М.И.,
Пышкало А.М.).
Любая задача представляет собой требование или
вопрос, на который надо найти ответ, опираясь и
учитывая те условия, которые указаны в ней
(Фридман Л.М., Турецкий Е.Н.).

4.

Функции задач в начальном курсе
математики
Способствуют умственному развитию детей (логическое
мышление, мыслительные операции, умозаключения)
Воспитательное значение (самостоятельность, трудолюбие,
настойчивость, терпение)
Способствуют формированию основ материалистического
мировоззрения (абстрактные понятия «число» и «цифра»
имеют корни в реальной жизни)
Углубляются представления о реальной действительности
Формируются основные понятия
Формируются вычислительные навыки

5.

Текстовая
задача
–
это
математическое задание, в котором можно
выделить условие и требование (указание, что
нужно найти) или вопрос, ответ на который
можно получить с помощью арифметических
действий.

6.

ЗАДАЧА
УСЛОВИЕ – та часть, где содержатся сведения об
известных и неизвестных значениях величин, об
отношениях между ними.
ТРЕБОВАНИЕ - указание на то, что нужно найти.
Для каждого ТРЕБОВАНИЯ применяется
определенный
МЕТОД или СПОСОБ ДЕЙСТВИЯ.

7.

В зависимости от СПОСОБА ДЕЙСТВИЯ различают
ВИДЫ ЗАДАЧ на построение, доказательство ,
преобразование, комбинаторные задачи, арифметические
задачи .
Понятие ЗАДАЧА в начальных классах – арифметическая
задача (текст, в котором находят отражение
количественные отношения между реальными
объектами)
Арифметическая = текстовая, сюжетная, вычислительная.

8.

1. В сюжетах – практические ситуации из жизни ребенка. Это помогает ему
ОСОЗНАТЬ реальные количественные отношения между различными
объектами ( величинами) и тем самым УГЛУБИТЬ и РАСШИРИТЬ свои
представления о реальной действительности.
2. РЕШЕНИЕ этих задач позволяет ребенку ОСОЗНАТЬ практическую
значимость тех математических ПОНЯТИЙ, которыми он овладеет в
начальном курсе математики.
3. В процессе их решения у ребенка формируются УМЕНИЯ, необходимые для
решения любой задачи: выделять ДАННЫЕ, ИСКОМОЕ, УСЛОВИЕ и
ВОПРОС, УСТАНАВЛИВАТЬ ЗАВИСИМОСТЬ между ними, строить
УМОЗАКЛЮЧЕНИЯ, МОДЕЛИРОВАТЬ, ПРОВЕРЯТЬ полученный
результат.

9.

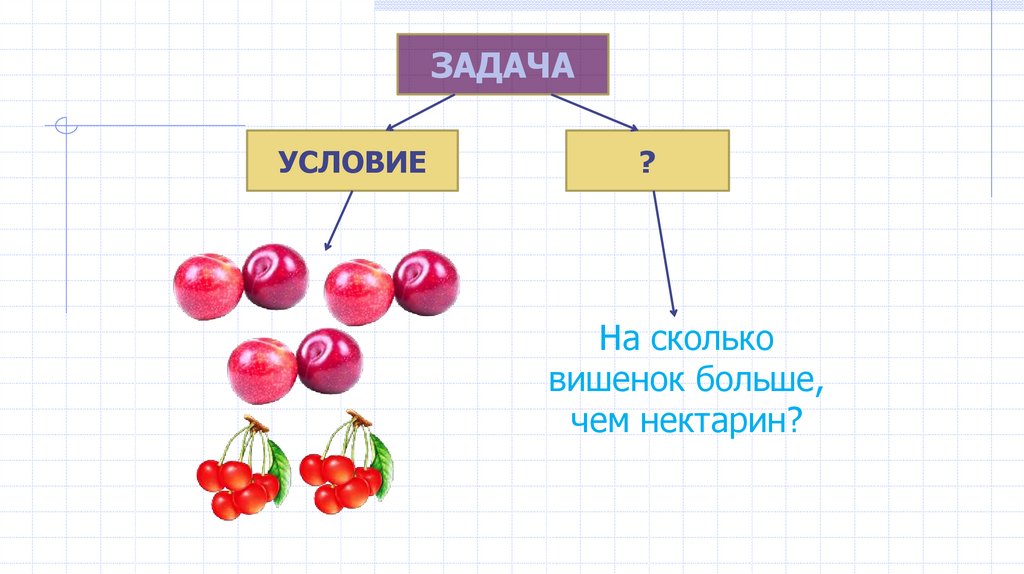
ЗАДАЧА
УСЛОВИЕ
?
На сколько
вишенок больше,
чем нектарин?

10.

Классификация текстовых задач
1 класс
1. Задачи на нахождение суммы (на сложение).
2. Задачи на увеличение и уменьшение числа на
несколько единиц.
3. Задачи на нахождение остатка (на вычитание).

11.

4. Задачи на нахождение неизвестного слагаемого.
5. Задачи на разностное сравнение.
6. Составные задачи на нахождение суммы.
7. Составные задачи на нахождение остатка.

12.

2 класс
1. Простые задачи на нахождение неизвестного
вычитаемого.
2. Простые задачи на нахождение уменьшаемого.
3. Составные задачи на нахождение слагаемого и
вычитаемого.
4. Составные задачи на нахождение третьего
слагаемого.
5. Составные задачи на нахождение уменьшаемого.

13.

6. Составные задачи на нахождение суммы.
7. Составные задачи на разностное сравнение.
8. Простые задачи на нахождение произведения (на
умножение).
9. Задачи на деление по содержанию и на равные части.
10.Задачи на нахождение периметра и сторон
геометрических фигур.

14.

3 класс
1. Задачи на увеличение и уменьшение числа в несколько
раз.
2. Задачи на кратное сравнение.
3. Задачи на приведение к единице.
4. Составные задачи на нахождение уменьшаемого,
вычитаемого, разности.
5. Составные задачи на кратное и разностное сравнение.

15.

6. Задачи на нахождение суммы двух произведений.
7. Составные задачи на нахождение неизвестного
слагаемого.
8. Составные задачи на нахождение суммы.
9. Простые и составные задачи, раскрывающие
зависимость между группами величин.

16.

10. Составные задачи на деление суммы на число.
11. Задачи на деление с остатком.
12. Задачи на нахождение числа по доле и доли по числу.
13. Задачи на нахождение периметра и сторон
геометрических фигур, площади квадрата,
прямоугольника.

17.

4 класс
1. Простые задачи на движение.
2. Задачи на встречное движение.
3. Задачи на движение в одном направлении.
4. Задачи на движение в противоположных направлениях.
5. Задачи с косвенными вопросами.

18.

6. Задачи на пропорциональное деление.
7. Задачи на нахождение неизвестного по двум
разностям.
8. Задачи на нахождение числа по доле и доли по числу.
9. Составные задачи на нахождение площади.

19.

Этапы решения текстовой задачи
Этапы решения задачи
М.А.Бантова
Л.М.Фридман
А.В.Тихоненко
1. Ознакомление с содержанием задачи.
2. Поиск плана решения.
3. Выполнение решения задачи.
4. Проверка решения задачи.
1. Анализ задачи.
2. Схематическая запись задачи.
3. Поиск способа решения задачи.
4. Осуществление решения задачи.
5. Проверка решения задачи.
6. Исследование задачи.
7. Формулирование ответа задачи.
8. Анализ решения задачи.
1. Чтение и осмысление текста задачи.
2. Выявление в тексте задачи условия и вопроса.
3. Установление связи между условием и вопросом.
4. Составление плана решения задачи и выбор
арифметического действия для ее решения.
5. Запись решения и ответа задачи.
6. Работа над задачей после ее решения.

20.

Решение задачи
Решение задачи - ответ на вопрос, результат
выполнения арифметических или других
действий.
Решение задачи - это выполнение действий,
которые в итоге дают значение искомой
величины.
Решение задачи - это догадка о том, какие нужны
действия и в какой последовательности их нужно
выполнять (если их несколько), чтобы получить
значение искомой величины (способ и метод
решения).

21.

Научить решать задачу – значит
научить раскрывать связи между
данными и искомыми, заданными в
условии задачи, на основе чего
выбирать, а затем выполнять
арифметические действия
(рационально) и отвечать на вопрос
задачи.

22.

Способы решения задачи
Практический (дети действуют непосредственно либо с реальными
объектами, либо с предметными моделями или изображениями этих
объектов и находят ответ на требование задачи с помощью
наблюдения, сравнения (измерения), счета).
Графический (учащиеся используют числовой луч, чертежи, где
изображения осуществляются в натуральную величину или в масштабе,
а ответ на требование задачи получается нахождением
соответствующих точек на луче, счетом и измерением искомой
величины на графической модели).
Алгебраический (уч-ся составляют простейшие уравнения и, решая их,
находят ответ на требование задачи).
Логический (дети выстраивают цепочку рассуждений, приводящих к
искомому заключению)
Схематическое моделирование
Комбинированный (используется сочетание различных методов)
Арифметический

23.

По действиям с устным пояснением
По действиям с письменным пояснением
По действиям с вопросами
Выражением

24.

преобразование текстов, не являющихся задачами, в
задачи;
изменение условия или вопроса так, чтобы действий
в решении стало больше (меньше);
сравнение задач;
составление задач самими учащимися;
решение задач с лишними (недостающими) данными;
изменение текста задачи так, чтобы в ее решении
появилось обратное действие;
выбор вопроса к условию;
выбор условия к заданному вопросу;
выбор схемы;
выбор решения.

25.

краткую запись с использованием общепринятых
условных обозначений (требует внимательного
чтения текста задачи, позволяет установить
взаимосвязь между величинами);
графическое моделирование задачи;
таблицу;
схематическое моделирование;
рисунок;
предметное моделирование.

26.

Общая характеристика работы
над задачей:
Подготовительная работа.
Работа по разъяснению текста задачи.
Фронтальная беседа по тексту задачи.
Наглядная интерпретация задачи.
Разбор задачи – поиск пути решения и
составления плана решения задачи.
Запись решения и ответа.
Решение задачи другим способом.
Проверка решения задачи.
Работа над задачей после ее решения.

27.

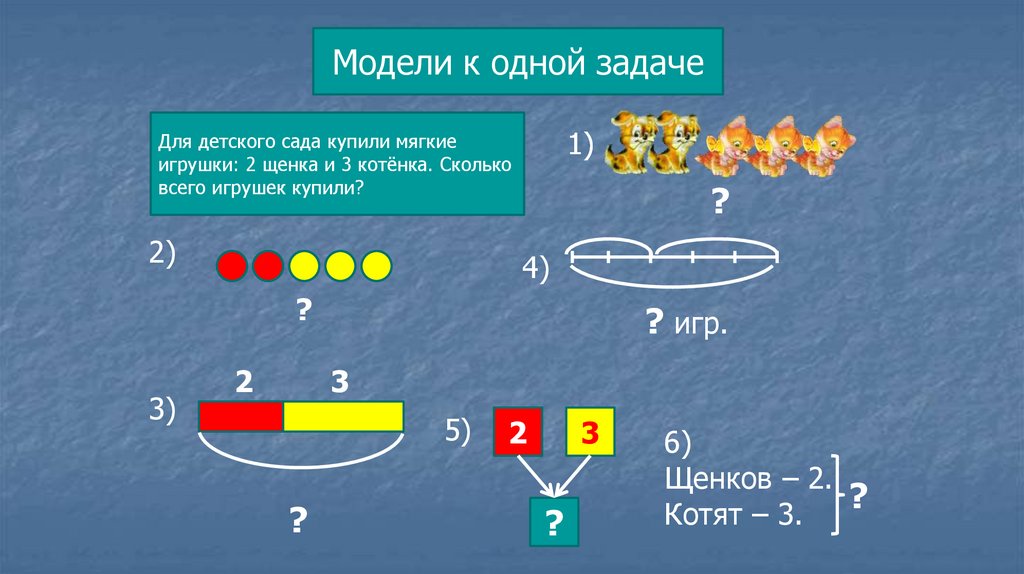
Модели к одной задаче
1)
Для детского сада купили мягкие
игрушки: 2 щенка и 3 котёнка. Сколько
всего игрушек купили?
2)
?
4)
?
3)
2
? игр.
3
5)
?
2
3
?
6)
Щенков – 2.
?
Котят – 3.