Лекция_6логика_1курс — копия

1. Лекции по информатике раздел «Элементы алгебры логики» для студентов 1 курса преподаватель Е.А.Зелинская

2.

Алгебра логики
Среди задач, для решения которых
используется компьютер,
немало так называемых “логических”
(например, про козу, капусту и волка).
При решении этих задач важным
является умение рассуждать.

3.

Алгебра логики
Компьютер может воспринимать
всего два вида сигналов: 0 и 1 (есть
контакт или нет контакта).
Каким образом можно перевести
сложные логические умозаключения
на язык, понятный компьютеру?
Ответ на этот вопрос дает
алгебра логики.

4.

Алгебра логики
Основоположником математической
логики считают великого немецкого
математика и философа
Вильгельма Лейбница (XVII век).
Его идеи развил в середине XIX века
английский математик Джордж Буль
(отец известной писательницы Этель
Войнич, автора романа “Овод”).

5.

Алгебра логики
Джордж Буль ввел для логических
построений особую алгебру –
алгебру логики.
В ней символами обозначались не
числа, а высказывания.

6.

Алгебра логики
Булева алгебра (алгебра логики)
применима к любым переменным,
которые могут принимать только два
значения (истина/ложь, 1 или 0), что
соответствует состоянию контактов:
вкл/выкл.
Поэтому алгебра логики лежит в основе
электрических и электронных
переключателей и схем, используемых в
компьютере.

7.

Алгебра логики
Высказывание – утверждение, о
котором можно судить, истинно оно
или ложно.
Высказывания обозначаются заглавными
буквами латинского алфавита.
Пример. A: “Париж – столица Нигерии”
A = 0 (высказывание A ложно)
B: “Москва – столица России”
B = 1 (высказывание B истинно)

8.

Алгебра логики
Простым высказыванием называется
высказывание, о котором точно можно
сказать истинно оно или ложно.
Из простых высказываний можно
составить сложные высказывания с
помощью логических операций.
Значение истинности сложного высказывания
определяется значениями истинности
составляющих его простых высказываний.

9.

Логические операции
I. Отрицание
A:
“Нил – озеро в Америке”
Ā:
“Нил не является озером в
Америке”
A=0
Ā=1

10.

Логические операции
Таблица истинности отрицания
A
Ā
0
1
1
0

11.

Логические операции
II. Конъюнкция
Конъюнкция является
логическим умножением
и соответствует союзу “И”.
Обозначение операции конъюнкция:
Λ

12.

Логические операции
A:
B:
“Гоголь – писатель”
“Пушкин – космонавт”
A=1
B=0
AΛB=0
Конъюнкция двух простых высказываний
истинна тогда и только тогда, когда оба
эти высказывания истинны.

13.

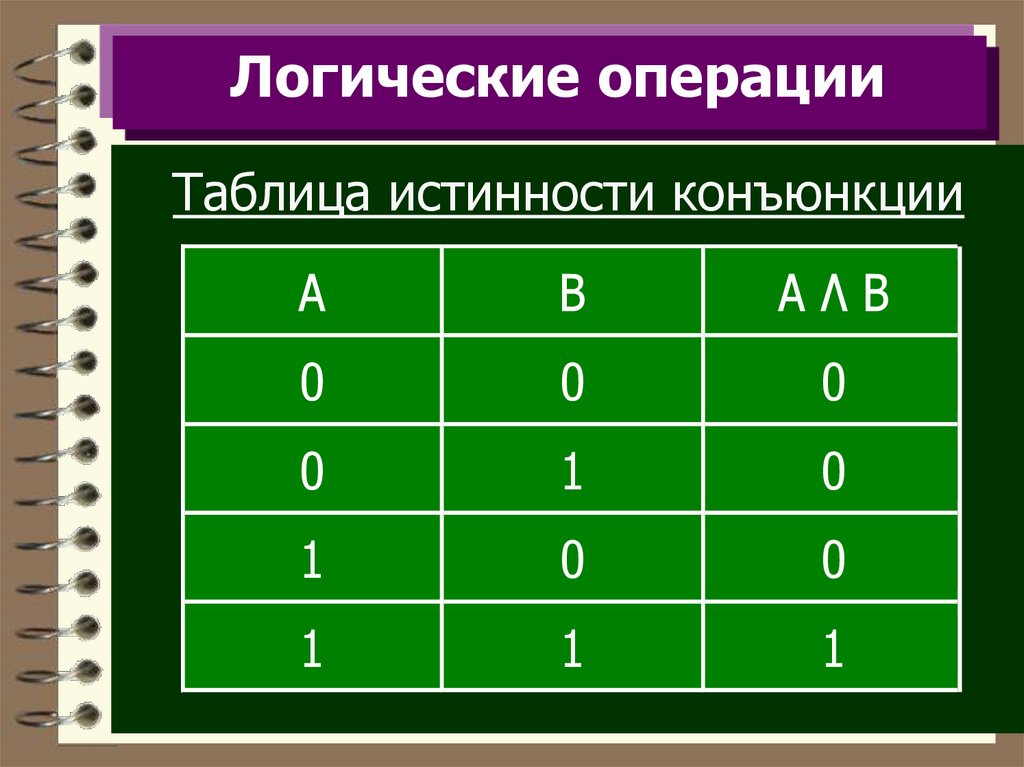
Логические операции
Таблица истинности конъюнкции
A
B
AΛB
0
0
0
0
1
0
1
0
0
1
1
1

14.

Логические операции
III. Дизъюнкция
Дизъюнкция является
логическим сложением
и соответствует союзу “ИЛИ”.
Обозначение операции дизъюнкции:
V

15.

Логические операции
A: “В летнюю сессию 1 курс сдает
экзамен по математике”
B: “В летнюю сессию 1 курс сдает
экзамен по геодезии”
A = 1, B = 0
AVB=1
Дизъюнкция двух простых высказываний
истинна тогда и только тогда, когда хотя
бы одно из этих высказываний истинно.

16.

Логические операции
Таблица истинности дизъюнкции
A
B
AVB
0
0
0
0
1
1
1
0
1
1
1
1

17.

Логические операции
Порядок выполнения логических
операций:
1) отрицание,
2) конъюнкция
(логическое умножение),
3) дизъюнкция
(логическое сложение).

18.

Логические операции
Задача 1 Составить таблицу истинности
для формулы: A Λ ( B V Ā )
A B Ā BVĀ AΛ(BVĀ)
0
0
0
1
1
0
1
1

19.

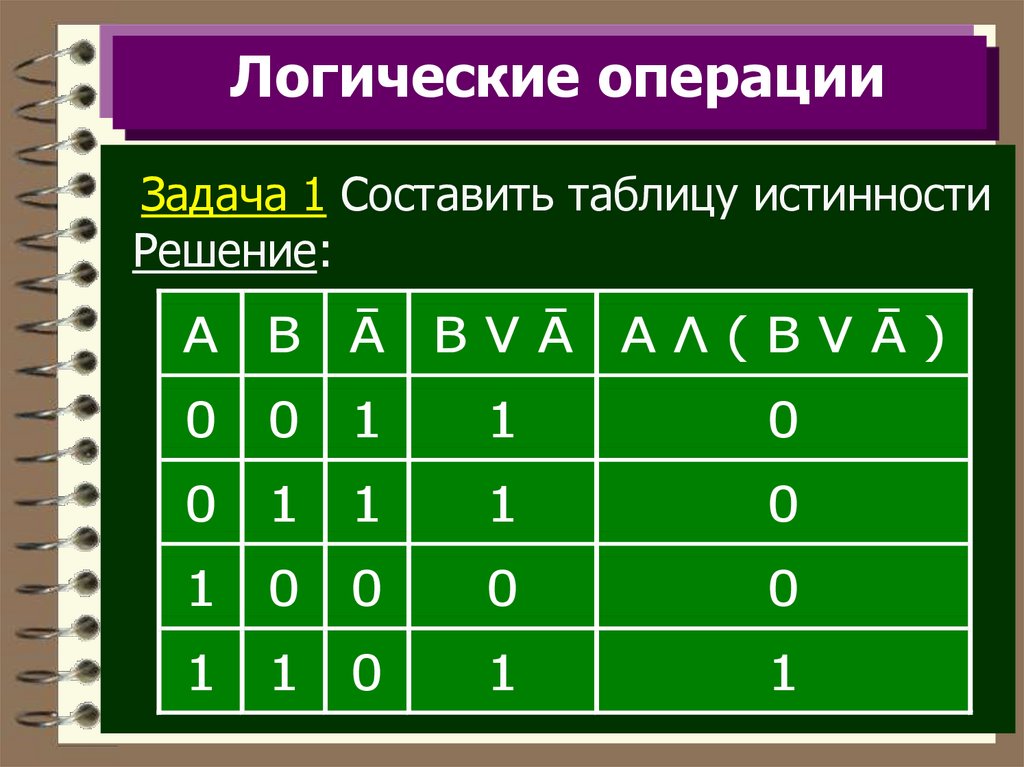
Логические операции
Задача 1 Составить таблицу истинности
Решение:
A
B Ā
BVĀ AΛ(BVĀ)
0
0
1
1
0
0
1
1
1
0
1
0
0
0
0
1
1
0
1
1

20.

Логические операции
Задача 2 Составить таблицы
истинности для следующих формул:
а) A Λ B V B
б) A Λ Ā V B Λ B
в) A Λ B V ( Ā V B )

21.

Логические операции
Две формулы называются
равносильными, если они принимают
одинаковые значения истинности при
одинаковых наборах значений
входящих в них переменных.
Задача 3 Показать равносильность
следующих формул:
AΛ(ĀVB)
и AΛĀVAΛB

22.

Логические операции
Задача 4 Выделите в сложных
высказываниях простые и
обозначьте их буквами.
Представьте эти сложные
высказывания в виде формул.
а) В воскресенье мы поедем на
дачу или на рыбалку, но на
рыбалке уху варить не будем.

23.

Логические операции
Задача 4 (a)
Решение:
A: “В воскресенье мы поедем на
дачу”
B: “В воскресенье мы поедем на
рыбалку”
C: “Сварим уху”
AVBΛС

24.

Логические операции
Задача 4 Выделите в сложных
высказываниях простые и
обозначьте их буквами.
Представьте эти сложные
высказывания в виде формул.
б) Число 156 делится на 3 и 4, но
не делится на 7.

25.

Логические операции
Задача 4 (б)
Решение:
A: “Число 156 делится на 3”
B: “Число 156 делится на 4”
C: “Число 156 делится на 7”
AΛBΛС

26.

Логические операции
Задача 4 Выделите в сложных
высказываниях простые и
обозначьте их буквами.
Представьте эти сложные
высказывания в виде формул.
в) На каникулах я поеду на
экскурсию в Петродворец или
Ломоносов, а моя сестра
поедет отдыхать в Ялту или Адлер.

27.

Логические операции
Задача 4 (в)
Решение:
A: “На каникулах я поеду на экскурсию в
Петродворец”
B: “На каникулах я поеду на
экскурсию в Ломоносов”
C: “Моя сестра поедет отдыхать в Ялту”
D: “Моя сестра поедет отдыхать в Адлер”
( A V B ) Λ (C V D )

28.

Логические операции
Задача 5 Даны простые высказывания:
A: “Доктор Ватсон – отставной офицер”
B: “Д-р Ватсон – друг Шерлока Холмса”
C: “Д-р Ватсон окончил университет”
Составить сложные высказывания,
используя следующие формулы:
а) B V A Λ C
б) B Λ C Λ Ā