Сложные высказывания. Основы формальной логики. Тема 5

1.

Основы формальной
логики
Тема 5
Сложные высказывания

2.

Сложные высказывания
Исчисление высказываний
• Понятие о сложном и простом высказывании
Виды сложных высказываний
Отрицание
Конъюнкция
Дизъюнкция
Исключающая (строгая) дизъюнкция
Импликация
Эквиваленция (эквивалентность)
Логические отношения между сложными высказываниям и
их членами
Функция истинности
• Вычисление функции истинности
• Равносильные формулы

3.

Исчисление высказываний
Элементарные высказывания – высказывания, не содержащие
логических постоянных.
Сложные высказывания – высказывания, содержащие логические
постоянные.
Логические постоянные – логические союзы (связки) и кванторы.
Логические (пропозициональные) связки – слова и
словосочетания «не», «неверно, что», «и», «или», «либо..., либо»,
«если..., то», «тогда и только тогда, когда» и др., а также
равнозначные им по смыслу слова и словосочетания.
Кванторы – словосочетания «для всех… имеет место, что», «для
некоторых… имеет место, что», а также равнозначные им по
смыслу слова и словосочетания.

4.

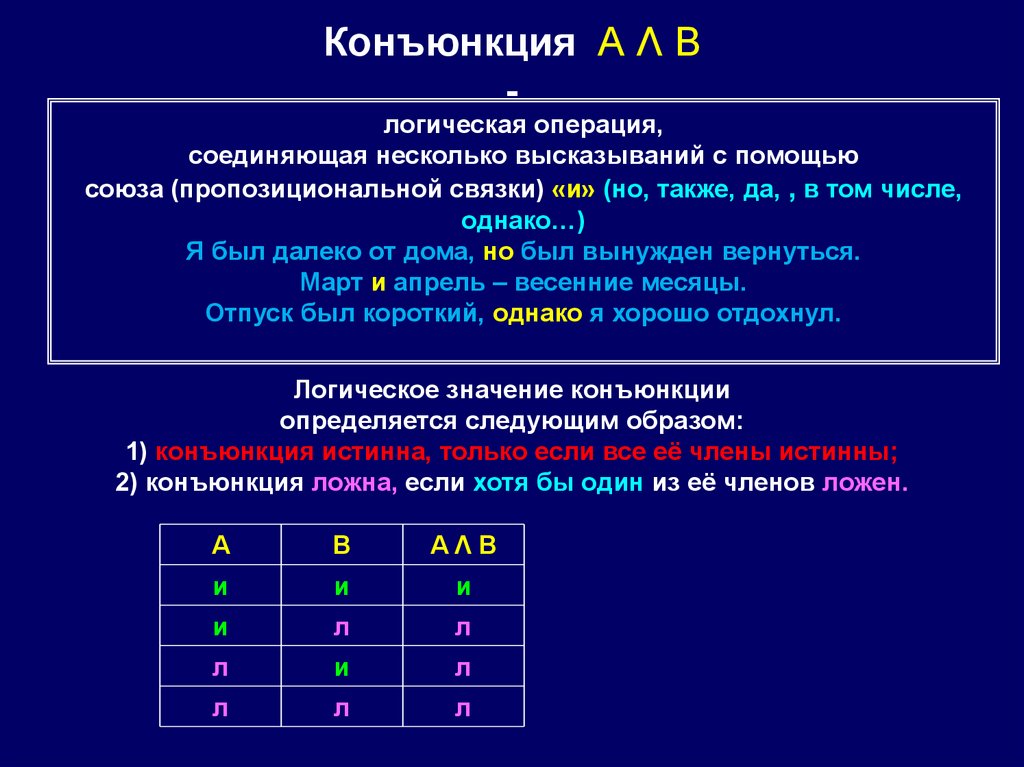
Конъюнкция A Λ B
-
логическая операция,
соединяющая несколько высказываний с помощью
союза (пропозициональной связки) «и» (но, также, да, , в том числе,
однако…)
Я был далеко от дома, но был вынужден вернуться.
Март и апрель – весенние месяцы.
Отпуск был короткий, однако я хорошо отдохнул.
Логическое значение конъюнкции
определяется следующим образом:
1) конъюнкция истинна, только если все её члены истинны;
2) конъюнкция ложна, если хотя бы один из её членов ложен.
A
B
AΛ B
и
и
и
и
л
л
л
и
л
л
л
л

5.

Дизъюнкция –
логическая операция,
соединяющая несколько высказываний с помощью
союза (пропозициональной связки) «или».
Дизъюнкция:
- Слабая (неисключающая, мягкая) «или» / «и» A V B
- Сильная (исключающая, жесткая) «или» / «либо» A V B
- Слабая: увеличение рентабельности может быть достигнуто путем
повышения производительности труда или снижения себестоимости
продукции
- Сильная: я поеду в отпуск на машине или полечу на самолете

6.

Логическое значение слабой дизъюнкции
определяется следующим образом:
1) дизъюнкция истинна, если хотя бы один из её членов
истинен;
2) дизъюнкция ложна, только если все её члены ложны.
A
B
AVB
и
и
и
и
л
и
л
и
и
л
л
л

7.

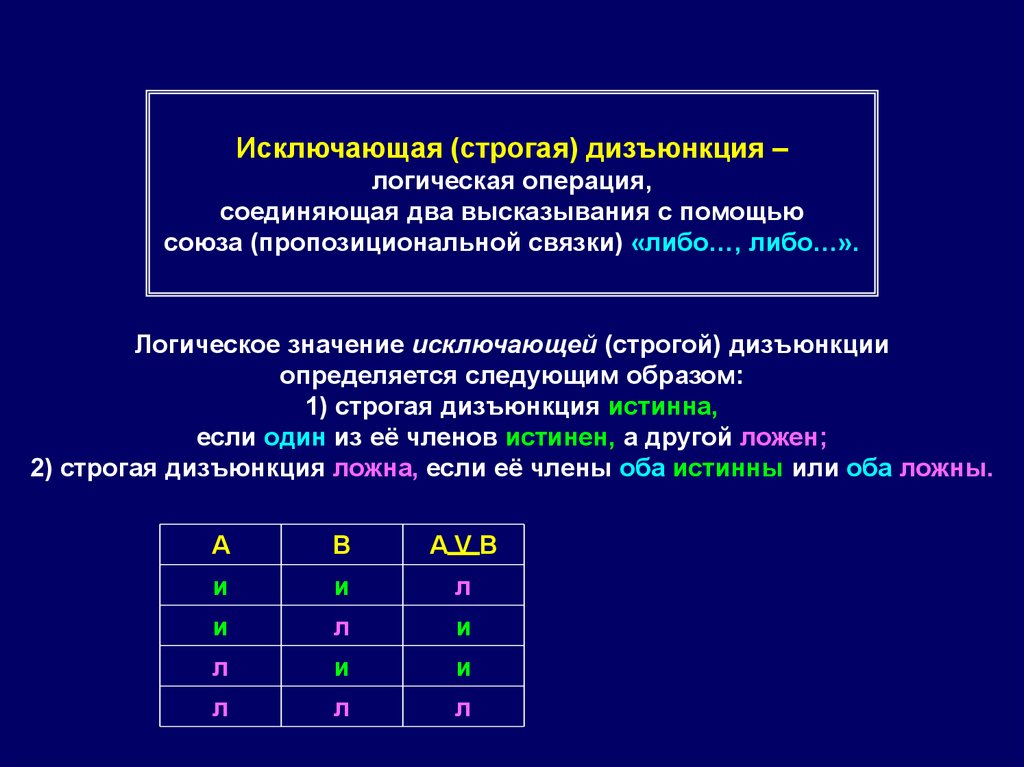
Исключающая (строгая) дизъюнкция –
логическая операция,
соединяющая два высказывания с помощью
союза (пропозициональной связки) «либо…, либо…».
Логическое значение исключающей (строгой) дизъюнкции
определяется следующим образом:
1) строгая дизъюнкция истинна,
если один из её членов истинен, а другой ложен;
2) строгая дизъюнкция ложна, если её члены оба истинны или оба ложны.
A
B
AVB
и
и
л
и
л
и
л
и
и
л
л
л

8.

Импликация A → B
Импликация (логическое следование)–
логическая операция,
соединяющая два высказывания с помощью
союза (пропозициональной связки) «если…, то…».
Не соблюдается закон логической симметрии (коммуникативности):
Если А, то В не есть Если В, то А
Если прошел дождь, то улицы мокрые. НЕ ЕСТЬ
Если улицы мокрые, то прошел дождь.
Антецедент (лог.причина) –
первый член
импликации,
заключённый между союзом «если» и
частицей «то».
Консеквент (лог.следствие)–
второй член
импликации,
стоящий
после
частицы «то».

9.

Импликация
Логическое значение импликации определяется следующим образом:
1) импликация истинна во всех случаях, когда
антецедент ложен или консеквент истинен;
2) импликация ложна только если антецедент истинен, а консеквент
ложен
A
B
A→B
и
и
и
и
л
л
л
и
и
л
л
и

10.

Эквиваленция (эквивалентность) A ↔ B
Эквиваленция –
логическая операция, соединяющая два высказывания
с помощью союза (пропозициональной связки)
«если и только если…, то…» или «тогда и только тогда, когда…».
Логическое значение эквиваленции определяется следующим образом:
1) эквиваленция истинна, если её члены оба истинны или оба ложны;
2) эквиваленция ложна, если один из её членов истинен, а другой ложен.
A
B
A↔B
и
и
и
и
л
л
л
и
л
л
л
и

11.

Отрицание
:
Отрицание –
логическая операция, отрицающая истинность
(утверждающая ложность) некоторого высказывания,
в результате чего из данного высказывания
получается высказывание, контрадикторное исходному.

12.

Отрицание
Виды :
- Внутренне и внешнее.
- Я не люблю кофе с молоком, но в редких случаях могу
выпить капуччино.
- Неверно, что я люблю кофе с молоком и регулярно его
пью.
- Внутреннее : простое и двойное.
Я не был на
занятиях. Неправда, что я не был на занятии.
Логическое значение отрицания
определяется следующим образом:
1) отрицание ложно, если отрицаемое суждение истинно,
2) отрицание истинно, если отрицаемое суждение ложно.
A
~A
и
л
л
и

13.

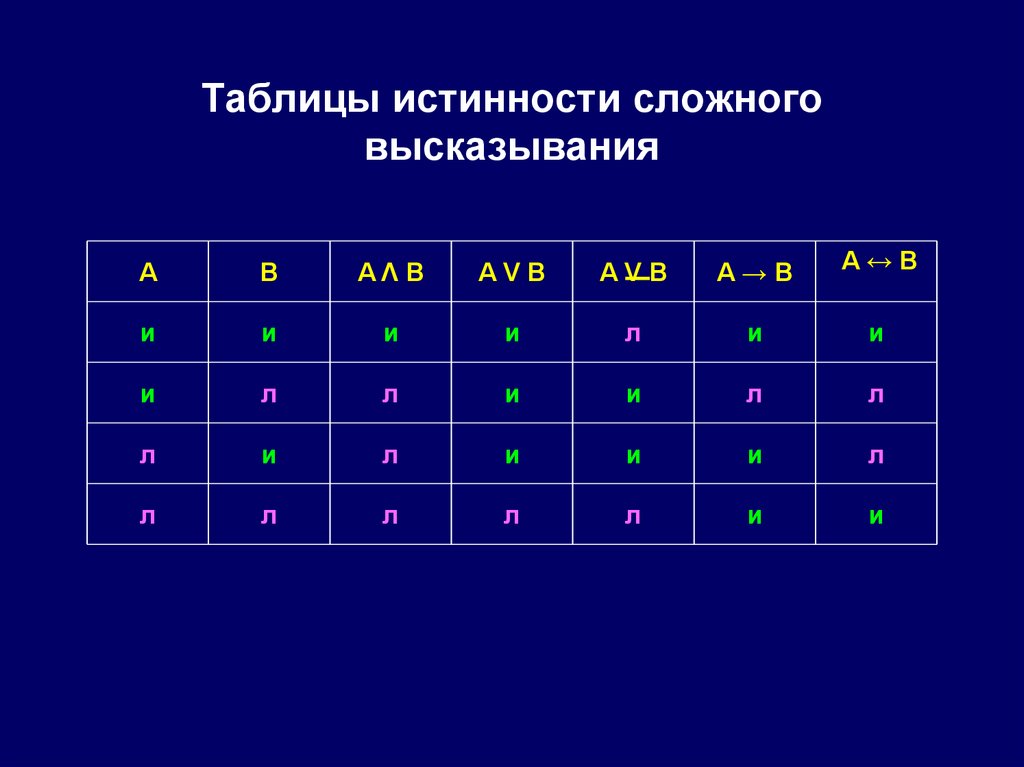
Таблицы истинности сложного
высказывания
A
B
AΛ B
AVB
AVB
A→B
A↔B
и
и
и
и
л
и
и
и
л
л
и
и
л
л
л
и
л
и
и
и
л
л
л
л
л
л
и
и

14.

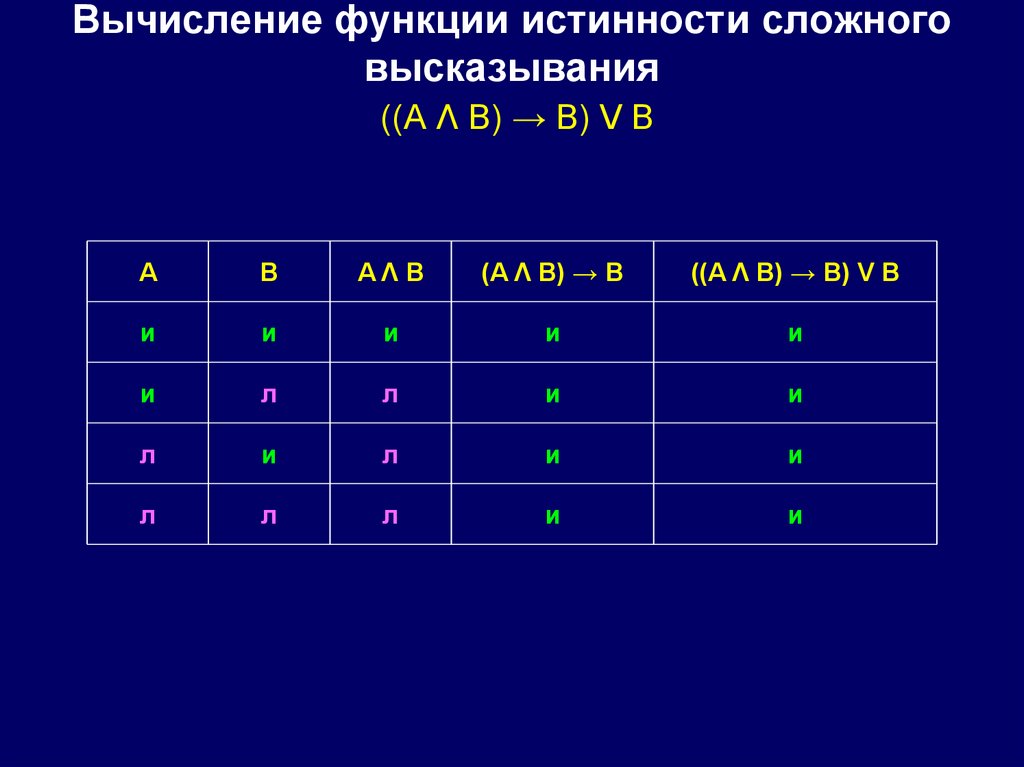
Вычисление функции истинности сложного
высказывания
((A Λ B) → B) V B
A
B
AΛ B
(A Λ B) → B
((A Λ B) → B) V B
и
и
и
и
и
и
л
л
и
и
л
и
л
и
и
л
л
л
и
и

15.

Исчисление истинности для
формул с внутренним и внешним отрицанием
A
B
~B
A→~B
A
B
A → B ~ (A → B)
и
и
л
л
и
и
и
л
и
л
и
и
и
л
л
и
л
и
л
и
л
и
л
л
и
и
л
л
и
и
л
л

16.

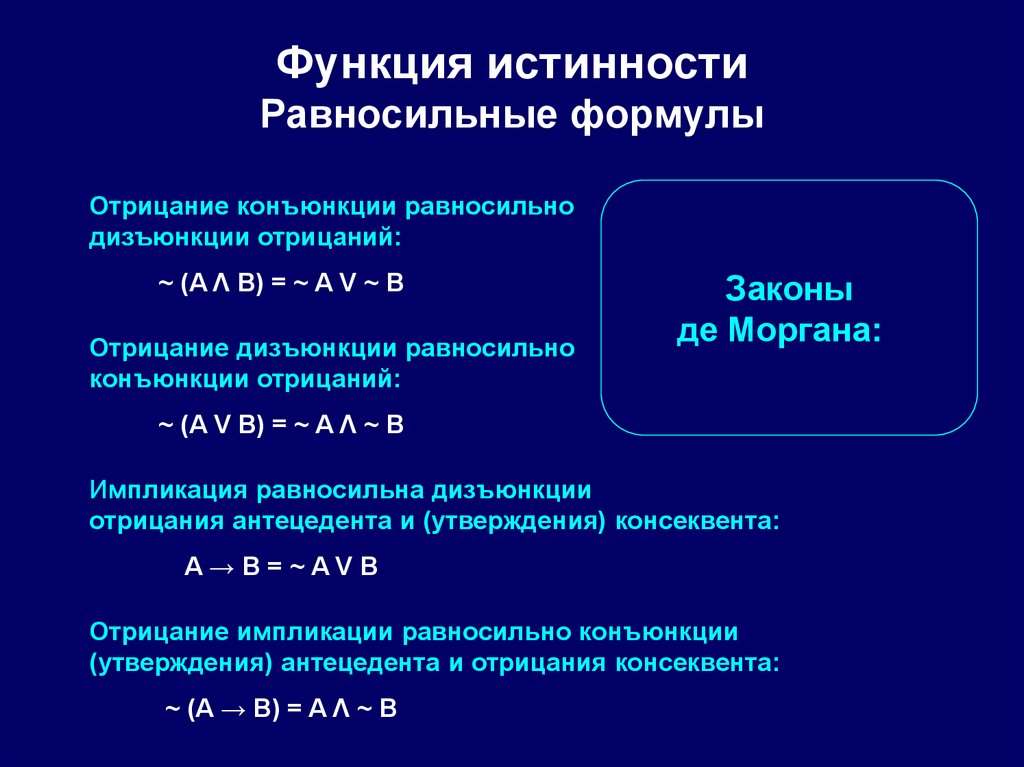
Функция истинности
Равносильные формулы
Отрицание конъюнкции равносильно
дизъюнкции отрицаний:
~ (A Λ B) = ~ A V ~ B
Отрицание дизъюнкции равносильно
конъюнкции отрицаний:
Законы
де Моргана:
~ (A V B) = ~ A Λ ~ B
Импликация равносильна дизъюнкции
отрицания антецедента и (утверждения) консеквента:
A→B=~AVB
Отрицание импликации равносильно конъюнкции
(утверждения) антецедента и отрицания консеквента:
~ (A → B) = A Λ ~ B