Алгебра логики

1. Алгебра логики

2.

Урок № 1
Логика как наука.
Формы человеческого
мышления
Хорошо думать —
значит победить
беспорядочность потока
мыслей.
Густав Гийом
Урок № 2
Логические операции.
Построение таблиц
истинности
Урок № 3
Логические законы.
Упрощение сложных
высказываний

3.

Урок № 1
Логика как наука.
Формы человеческого
мышления
Урок № 2
Логические операции.
Построение таблиц
истинности
Урок № 3
Логические законы.
Упрощение сложных
высказываний
Объяснение
материала
Об истории
логики
Область
применения
алгебры логики
Основные
понятия логики

4.

Урок № 1
Логика как наука.
Формы человеческого
мышления
Урок № 2
Логические операции.
Построение таблиц
истинности
Урок № 3
Логические законы.
Упрощение сложных
высказываний
Объяснение
материала
Логические
операции
Сложные
высказывания
Построение
таблиц
истинности
сложных
высказываний

5.

Урок № 1
Логика как наука.
Формы человеческого
мышления
Урок № 2
Логические операции.
Построение таблиц
истинности
Урок № 3
Логические законы.
Упрощение сложных
высказываний
Объяснение
материала
Законы логики
Упрощение
сложных
высказываний

6. Об истории логики

Термин логика происходит от древнегреческого
logos, означающего «слово, мысль, понятие,
рассуждение, закон».
Логика - это наука правильно
рассуждать, наука о формах и законах
человеческого мышления.
Задача логики - описать и исследовать те
способы рассуждений, которые являются
правильными.

7. Основоположник формальной логики

Аристотель
(384 - 322 гг. до н.э.)
Основоположник формальной логики

8.

Рене Декарт
(1596 - 1650)
Рекомендовал в логике использовать
общепринятые математические методы.

9. Предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной

Готфрид Вильгельм
Лейбниц
(1646 - 1716 )
Предложил использовать в логике
математическую символику и впервые
высказал мысль о возможности
применения в ней двоичной системы
счисления. Так зародилась
математическая, или символическая,
логика.

10. Основоположник алгебры логики (булевой алгебры)

Джордж Буль
(1815 - 1864)
Основоположник алгебры логики
(булевой алгебры)

11.

Большой вклад в становление и развитие математической
логики внесли многие выдающиеся математики и логики
XVI - XX веков, в том числе
М. В. Ломоносов А. Тьюринг Д. Гильберт
Г. Фреге
П. С. Новиков
К. Гедель
А. А. Марков
И. Кант
А. Н. Колмогоров

12. Область применения алгебры логики

Алгебра логики сегодня - раздел
математической логики, изучающий
строение (форму, структуру) сложных
логических высказываний и способы
установления их истинности с
помощью алгебраических методов.

13.

Мыслить логично - значит мыслить
точно и последовательно, не допуская
противоречий в своих рассуждениях,
уметь вскрывать логические ошибки.
Постижение науки логики дает возможность:
узнать законы, правила и приемы мышления;
анализировать правильность рассуждений;
оценивать истинность полученных
заключений.

14.  в вычислительной технике;  в логических построениях в математике;  в повседневных рассуждениях.

Практическое применение
булевой алгебры
в вычислительной технике;
в логических построениях в математике;
в повседневных рассуждениях.

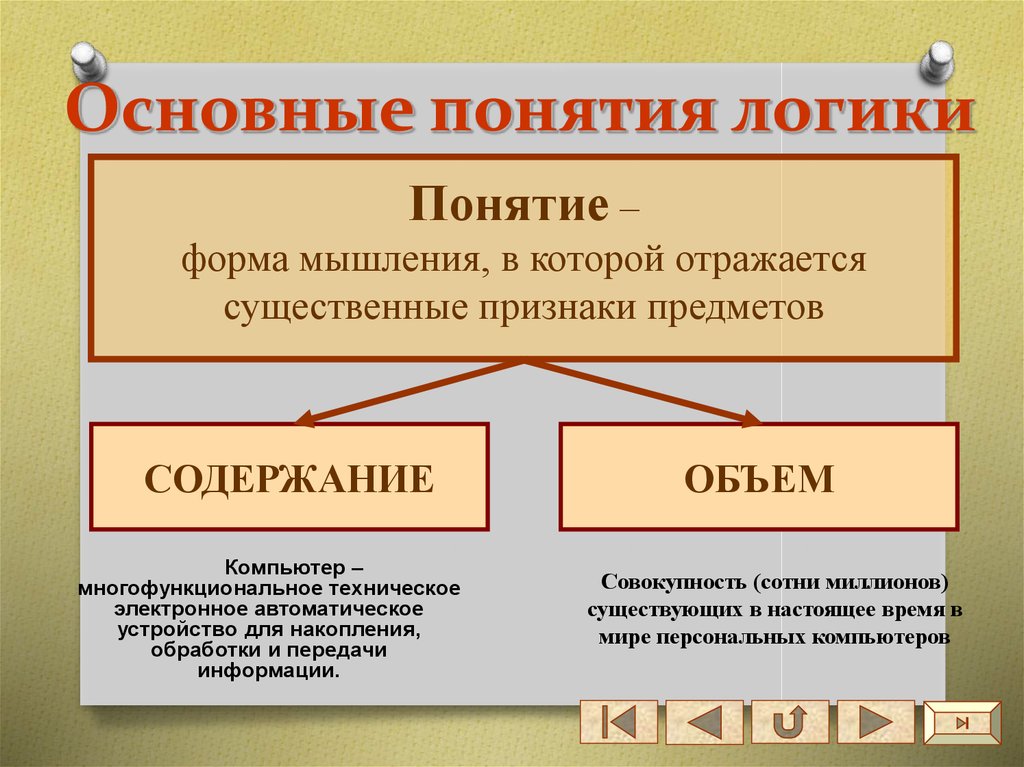
15. Основные понятия логики

Понятие –
форма мышления, в которой отражается
существенные признаки предметов
СОДЕРЖАНИЕ
Компьютер –
многофункциональное техническое
электронное автоматическое
устройство для накопления,
обработки и передачи
информации.
ОБЪЕМ
Совокупность (сотни миллионов)
существующих в настоящее время в
мире персональных компьютеров

16.

Виды понятий
O Несравнимые
– далекие друг от друга по своему
содержанию понятия, не имеющие
общих признаков.
O Сравнимые
– остальные.
O Совместимые
– объемы понятий совпадают
полностью или частично.
O Несовместимые – объемы понятий не совпадают
ни по одному элементу.

17.

Физкультминутка
Упражнение первое:
сжимать и разжимать кулаки. Повторить 4- 5
раз.
Упражнение второе:
вращать кистями рук в одну и другую сторону.
Повторить 4-5 раз.
Упражнение третье:
перевести взгляд быстро по диагонали:
направо вверх - налево вниз, потом прямо
вдаль на счет 1-6; затем налево вверх направо вниз и посмотреть вдаль на счет 1-6.
Повторить 4-5 раз.

18. Основные понятия логики

Суждение (высказывание, утверждение) форма мышления, в которой что-либо утверждается
или отрицается о предметах, их свойствах или
отношениях между ними.
Суждение (высказывание, утверждение)
- повествовательное предложение, относительно
которого можно сказать, истинно оно или ложно.

19. Не являются суждениями:

O Предложения, о которых Эта книга - информатика.
нельзя сказать, истинны Метеорологический
прогноз.
они или ложны.
O Вопросительные и
восклицательные
предложения.
O Предикаты (выражения о
Как мелодичны вы, песни,
Украины!
Верно ли, что сегодня
теплая погода?
5 +X =12
переменных) , в которых
X+Z<1
значения переменных не
Число Y кратно 3
определены.

20. Виды суждений

O Частные
– выражают конкретные факты.
O Общие
– характеризуют свойства групп
O Простые
–
O Сложные
–
O Равносильные –
(эквивалентные)
объектов (явлений).
не содержат в себе других
высказываний.
образованы из нескольких
простых с помощью
определенных способов
соединения.
одновременно истинные или
одновременно ложные.

21. Основные понятия логики

Умозаключение - форма мышления,
посредством которой из одного или нескольких
истинных суждений (посылок) по определенным
правилам вывода получают суждение-заключение.

22.

Вопросы и задания 1
С
У
Ж
Д
Е
Н
И
Е
Н
Е
С
У
Ж
Д
Е
Н
И
Е
Какие из перечисленных ниже предложений являются суждениями?
• Некоторые люди имеют голубые глаза.
• Вы были в театре?
• Мойте руки перед едой.
• Если будет дождь, то мы поедем за грибами.
• Завтра я сдам экзамен, либо останусь на второй год.
• Существую такие люди, которые не любят животных.
• Завтра я пойду на каток.
• Если я поеду туда, то смогу ли вернуться?
• IF X>1 THEN Y=0

23.

Вопросы и задания 2
Укажите для нижеприведенных высказываний, сложные они или простые:
С
Л
О
Ж
Н
Ы
Е
П
Р
О
С
Т
Ы
Е
• Если две прямые параллельны, то они пересекаются.
• Идет дождь.
• На следующем уроке будет либо контрольная работа, либо
свободный урок.
• Завтра или сегодня брат приедет к нам в гости.
• Треугольники с равными сторонами не равнобедренны.
• Завтра премьера в нашем театре.
• Это число не простое.
• Сегодня, завтра и каждый день я буду учиться.
• 7 + x x + c + 0,1 a
• Число 4 больше числа 2.

24.  Вопросы и задания 3

Вопросы и задания 3
Какие из перечисленных ниже предложений являются суждениями
и каково значение их истинности:
И
С
Т
И
Н
А
O "сижу и смотрю";
O "сумма внутренних углов треугольника
равна двум прямым углам";
O "верно ли, что π=3,1415926...?";
Л
О
Ж
Ь
O "44>88";
O "математическое доказательство";
O "Z + 5 = 45".

25.  Вопросы и задания 4

Вопросы и задания 4
Укажите, какие из суждений являются частными, а какие общими:
Ч
А
С
Т
Н
Ы
Е
О
Б
Щ
И
Е
O
(X + Y) (X - Y) = X2 - Y2;
O
"Любой ромб является параллелограммом";
O
"А3= А2, если А=1";
O
Если |А| = |В|, то А = В;
O
"Квадрат любого числа делится на 4";
O
"Меркурий - спутник Марса";
O
"Джордано Бруно - ученик Галилео Галилея";
O
"Не существует целого числа, куб которого оканчивается
цифрой 2 ".

26.

Физкульминутка
Упражнение первое:
резко зажмурить глаза на 2-3 секунды: и широко
открыть на 2-3 секунды, повторить упражнение 10
раз.
Упражнение второе:
часто-часто моргать глазами, повторить 10 раз.
Упражнение третье:
поднять глаза вверх, при этом голова остается в одном
положении, задержать взгляд на 2-3 секунды, затем
опустить глаза вниз и задержать взгляд на 2-3 секунды
повторить упражнение 10 раз .

27. Логические операции

– способ построения сложного высказывания
из данных высказываний, при котором
значение истинности сложного
высказывания полностью определяется
значениями истинности исходных
высказываний.

28.

Логическое отрицание -ИНВЕРСИЯ
Образуется из высказывания с помощью добавления
частицы «НЕ» к сказуемому или использования
оборота речи «НЕВЕРНО, ЧТО...»
Обозначение:
Ā, ¬А, не А, Примеры инверсии:
not А
А= «Неверно, что у меня
Таблица истинности:
А Ā
0
1
1
0
есть приставка Dendy»
В= «Я не знаю китайского
языка»
Инверсия высказывания истинная,
когда высказывание ложно, и ложна,
когда высказывание истинно.

29.

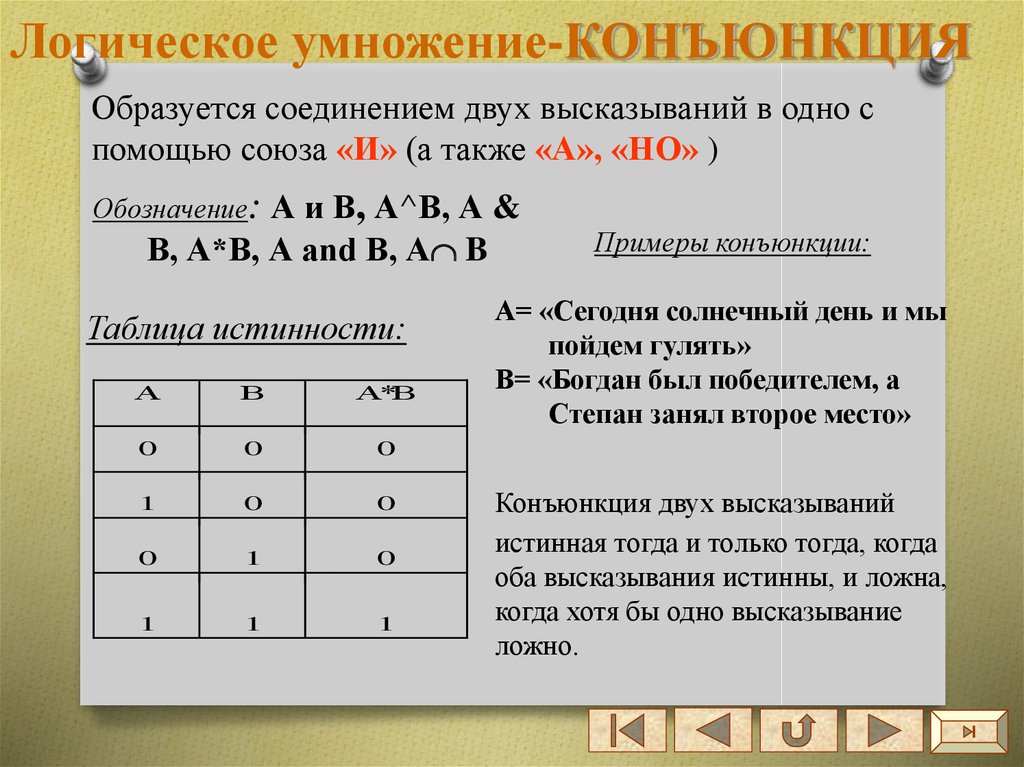
Логическое умножение-КОНЪЮНКЦИЯ
Образуется соединением двух высказываний в одно с
помощью союза «И» (а также «А», «НО» )
Обозначение: А и В, А^В, А &
В, А*В, А and B, А B
Таблица истинности:
А
В
А*В
0
0
0
1
0
0
0
1
0
1
1
1
Примеры конъюнкции:
А= «Сегодня солнечный день и мы
пойдем гулять»
В= «Богдан был победителем, а
Степан занял второе место»
Конъюнкция двух высказываний
истинная тогда и только тогда, когда
оба высказывания истинны, и ложна,
когда хотя бы одно высказывание
ложно.

30.

Логическое сложение -ДИЗЪЮНКЦИЯ
Образуется соединением двух высказываний в одно с
помощью союза «ИЛИ» (нестрогая), «ЛИБО» (строгая)
Обозначение: А или В, АV В,
А | В, А+В, А or B, А B;
A B, A xor B
Таблица истинности:
А
В
А+В
0
0
0
1
0
1
0
1
1
1
1
1
Примеры дизъюнкции:
А= «Снег пойдет ночью или утром»
В= «Он приедет сегодня либо
завтра»
Дизъюнкция двух высказываний
ложна тогда и только тогда, когда оба
высказывания ложны, и истинна, когда
хотя бы одно высказывание истинно.

31.

Логическое следование -ИМПЛИКАЦИЯ
Образуется соединением двух высказываний в одно с
помощью оборота речи «ЕСЛИ …, ТО ...»
Обозначение: А В, А В
Таблица истинности:
А
В
А В
0
0
1
1
0
0
0
1
1
1
1
1
Примеры импликации:
А= «Если число делится на 9, то оно
делится на 3»
В= «Если на улице дождь, то
асфальт мокрый»
Импликация двух высказываний
ложна тогда и только тогда, когда из
истинного высказывания следует
ложное.

32.

Логическое равенство -ЭКВИВАЛЕНТНОСТЬ
Образуется соединением двух высказываний в одно с
помощью оборота речи «… ТОГДА И ТОЛЬКО ТОГДА,
КОГДА ...»
Обозначение: А В, А В,
А=В, А В, А~В
Таблица истинности:
А
В
А В
0
0
1
1
0
0
0
1
0
1
1
1
Примеры эквивалентности:
А= «Число кратно 3 тогда и только
тогда, когда сумма цифр числа
делится нацело на 3»
В= «Угол называется прямым тогда
и только тогда, когда он равен
90°»
Эквивалентность двух высказываний
истинна тогда и только тогда, когда
оба высказывания истинны или оба
ложны.

33. Свойства логических операций

высказывание ложно
Инверсия истинна
Дизъюнкция ложна
Конъюнкция истинна
тогда
оба высказывания
ложны
истинны
и
Дизъюнкция истинна
только
Конъюнкция ложна
тогда,
когда
хотя бы одно
высказывание
истинно
ложно
Импликация ложна
из истинного высказывания
следует ложное высказывание
Эквивалентность
истинна
оба высказывания ложны или
оба высказывания истинны

34. Перевод логических операций на естественный язык

O Инверсия
O Конъюнкция
O
Дизъюнкция
O Импликация
O Эквивалентность
O не А; неверно, что А
O и А, и В; как А, так и В; А вместе с В;
А несмотря на В; А, в то время как В;
АиВ
O А или В; А либо В; либо А, либо В;
строго А или В
O
если А, то В; В, если А; В
необходимо для А; А достаточно для
В; А только тогда, когда В; В тогда,
когда А; все А есть В
O А эквивалентно В; А необходимо и
достаточно для В; А тогда и только
тогда, когда В

35. Приоритет логических операций

O инверсия
O конъюнкция
O дизъюнкция
O импликация
эквивалентность
Операции одного приоритета выполняются
слева направо.
Для изменения порядка действий
используются скобки.
O

36.

Пример 1
3
4
2
5
1
Дана формула: А V В С & D Ā
Порядок вычисления:
•Ā
— инверсия
• C&D
— конъюнкция
• АV В
— дизъюнкция
•АVВ С&D
— импликация
•АVВ С&D Ā
— эквивалентность

37.

Пример 2
4
2
3
5
1
Дана формула: А V (В С) & D Ā
Порядок вычисления:
•Ā
— инверсия
• (В C)
— импликация в скобках
• (В С) & D
— конъюнкция
• А V (В С) & D
— дизъюнкция
• А V (В С) & D Ā
— эквивалентность

38. Сложные высказывания

Если несколько простых высказываний объединены в
одно с помощью логических операций, то такое
высказывание называется сложным.
Примеры сложных высказываний:
Сло ж
ное высказывание
Е = «Идет дождь, а
меня нет зонта »
Сос тавляющие прос тые
высказывания
у А = «Идет дождь »;
В = «У меня есть зонт »
Е = «Когда живется весело, А = «Живется весело»;
то работа спорится»
В = «Работа спорится»
Е = «Идет налево – песнь А = «Идет налево»;
заводит, направо – сказку В = «Идет направо»;
говорит »
С = «Песнь заводит »;
D = «Сказку говорит »
Форма сло ж
ного
высказывания
Е =А & В
Е = А В
Е = (А С) V (В D)

39. Тождественно истинные, тождественно ложные и эквивалентные высказывания

Если высказывание истинно при всех значениях входящих в
него переменных, то такое высказывание называется
тождественно истинным или тавтологией (обозначается
константой 1).
Например, Демократ - человек, исповедующий демократические убеждения.
Если высказывание ложно при всех значениях входящих в него
переменных, то такое высказывание называется тождественно
ложным (обозначается константой 0).
Например, Компьютер включен, и компьютер выключен.
Если значения сложных высказываний совпадают на всех
возможных наборах значений входящих в них переменных, то
такие высказывания называется равносильными,
тождественными, эквивалентными.

40. Задача № 1

Укажите значения истинности простых
высказываний, при которых суждение
«Если у меня будет свободное время, и я сдам
экзамены, то я поеду отдыхать»
ложно.

41. Задача № 1

Решение
В = «У меня будет свободное время»
Е = «Я сдам экзамены»
А = «Я поеду отдыхать»
B&Ē Ā

42. Построение таблиц истинности сложных высказываний

Построить таблицу истинности для высказывания
B &Ē Ā
Алгоритм построения таблицы истинности сложного высказывания
( на примере n=3):
• вычислить количество строк и столбцов таблицы истинности
(количество строк - 2n +2, количество столбцов равно сумме количества
переменных (n) и количества логических операций, входящих в сложное
высказывание);
• начертить таблицу и заполнить заголовок в соответствии с приоритетом
логических операций;
• заполнить первые 3 столбца с учетом всех возможных комбинаций
значений переменных;
• заполнить остальные столбцы таблицы в соответствии с таблицами
истинности логических операций, причем при заполнении каждого
столбца операции выполняются над значениями столбцов, расположенных
левее заполняемого.

43.

В & Ē Ā
В Е А Ē Ā В & Ē В &Ē Ā
1
2
3
0
0
0
0
0
1
0
0
1
1
0
1
1
1
0
0
1
1
0
1
0
1
1
1
4(2) 5(3)
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
6 (1) * (4)
0
7 (6) (5)
1
0
1
0
0
1
1
1
1
1
0
0
1
0
1

44. Законы логики

45.

Закон тождества:
в процессе определенного рассуждения
всякое понятие и суждение должны
быть тождественны самим себе.
А=А

46.

Закон непротиворечия:
невозможно, чтобы одно и тоже в
одно и тоже время было и не было
присуще одному и тому же в одном и
том же отношении. То есть
невозможно что-то одновременно
утверждать и отрицать.
А&Ā=0

47.

Закон исключения
третьего:
из двух противоречащих суждений
одно истинно, другое ложно, а
третьего не дано.
А+Ā=1

48.

Закон достаточного
основания:
всякая истинная мысль должна быть
достаточно обоснована.

49.

Закон двойного
отрицания:
если отрицать дважды некоторое
высказывание, то в результате
получается исходное высказывание.
А =А

50.

Свойства констант:
отрицание
лжи есть
истина.
0=1
отрицание
истины
есть ложь.
1=0
Аv0=А
А&0=0
Аv1=1
А&1=A

51.

Закон идемпотентности:
АvА=А
А&А=A

52.

Законы коммутативности
(сочетательные законы):
операнды А и В в операциях
дизъюнкции и конъюнкции можно
менять местами.
АvВ=ВvА
А&В=В&А

53.

Законы ассоциативности
(распределительные законы):
если в выражении используется только
операция дизъюнкции или только операция
конъюнкции, то можно пренебрегать
скобками или произвольно их расставлять.
А v (В v C) = (А v В) v C
А & (В & C) = (А & В) & C

54.

Законы дистрибутивности:
А v (В & C) = (А v В) & (А v C)
А & (В v C) = (А & В) v (А & C)

55.

Законы поглощения:
А & (В v B) = А или
А & (А v В) = А или
(А v B) & B = А & B
А v В & B = А или
А v (А & В) = А или
(А & B) v B = А v B

56.

Законы де Моргана:
отрицание дизъюнкции есть конъюнкция
отрицаний. Отрицание конъюнкции есть
дизъюнкция отрицаний.
А v В = А & В или
АvB=А&B
А & В = А v В или
А&B=АvB

57.

Правило замены операции
импликации:
А В =АvВ

58.

Правило замены операции
эквивалентности:
А В =В А
А В = (А v В) & (А v B)
А В = (А & В) v (А & B)
А В = (А В) & (B A)

59. Доказательство логических законов

построить таблицу истинности для правой и
левой частей равенства;
O выполнить эквивалентные преобразования
над правой и левой частями равенства для
приведения их к одному виду;
O с помощью диаграмм Эйлера - Венна;
O путем правильных логических рассуждений.
O

60. Упрощение сложных высказываний

61.

X=X&1
- по свойствам констант;
X=Xv0
1=АvA
- по закону исключения третьего;
0=Z&Z
- по закону исключения третьего;
B=BvB=BvBvBvB
C=C&C=C&C&C&C
E=E
- по законам
идемпотентности;
- по закону двойного отрицания.

62. Задача № 2 «Уроки логики»

На вопрос, кто из трех школьников
изучал логику, был получен
правильный ответ:
если изучал первый, то изучал и
второй, но не верно, что если
изучал третий, то изучал и второй.
Кто из учащихся изучал логику?

63. Задача № 2 «Уроки логики»

Решение:
Р1 = «Первый школьник изучал логику»
Р2 = «Второй школьник изучал логику»
Р3 = «Третий школьник изучал логику»

64. Задача № 2 «Уроки логики»

(Р1 → Р2) & (Р3 → Р2) =
= (P1 v P2) & (P3 v P2) =
= (P1 v P2) & (P3 & P2) =
= (P1 & P3 & P2) v (P2 & P3 & P2) =
=0
= (P1 & P3 & P2)

65.

Пример 3
Требуется упростить: А & B v A & B
По закону дистрибутивности вынесем А за
скобки:
А & B v A & B = А & (B v B) = А & 1 = A

66.

Пример 4
Требуется упростить: (А v B) & (A v B)
Способ 1. Применим закон дистрибутивности:
(А v B) & (A v B) = А v (B & B) = А v 0 = A
Способ 2. Перемножим скобки на основании того
же закона дистрибутивности:
(А v B) & (A v B) = А & А v А & B v B & А v B & B
= А v А & (B v B) v 0 = А v A & 1 = А v А = A

67.

Пример 5
Требуется упростить: X v X & Y
Представим Х как Х & 1, а 1 распишем по закону исключения
третьего как Y v Y, далее раскроем скобки:
X v X & Y = X & 1 v X & Y = X & (Y v Y) v X & Y= X & Y v
v X & Y v X & Y.
Закон имподентности позволяет добавить в выражение любое
из имеющихся в нем слагаемых. Добавим к полученному
выражению X & Y и сгруппируем слагаемые:
X&Yv X&YvX&Y=X&YvX&YvX&YvX&Y=
= (X & Y v X & Y) v (X & Y v X & Y) = X & (Y v Y) v Y &
& (X v X) = X & 1 v Y & 1 = X v Y.

68.

Пример 6
Требуется упростить: А & C v B & C v А & B
Добавим к последнему слагаемому С. Это делается
стандартным способом: умножим А & B на 1, а 1 распишем как
С v С:
A&C v B &C vA&B =A&C v B &C vA&B & 1 =A&C v
v B & C v А & B & (C v C) = A & C v B & C v A & B & C v A &
&B &C =A& C vA&B &C v B &C vA&B &C =
=
A & C & (1 v B) v B & C & (1 v А) = A & C v B & C

69.

Пример 7
Требуется упростить: X v Y
Применим закон де Моргана:
X v Y=X& Y=X&Y

70.

Пример 8
Требуется упростить: X & Y v X & Y v X & Z
В данном случае воспользуемся законом двойного отрицания:
X&YvX& YvX&Z=X&YvX& YvX&Z=
{раскроем одно отрицание}= (X & Y) & (X & Y) & (X & Z) =
= (X v Y) & (X v Y) & (X v Z) = {перемножим первую и вторую
скобки, упростим, а третью скобку оставим без
изменения}= (X & X v X & Y v X & Y v Y & Y) & (X v Z) =
= (X & Y v X & Y) & (X v Z) = {перемножим скобки,
упростим}= X & X & Y v X & Y & Z v X & Y v X & Y & Z =
= X & Y & Z v X & Y = {применим закон де Моргана}=
X & Y & Z & (X v Y) = (X v Y v Z) & (X v Y)
=

71. Физкульминутка

Упражнение 1.
Поднять глаза вверх, при этом голова остается в одном положении,
задержать взгляд на 2-3 секунды, затем опустить глаза вниз и
задержать взгляд на 2-3 секунды повторить упражнение 10 раз.
Упражнение 2.
Посмотреть вправо (не поворачивая головы), как можно дальше,
задержать взгляд на 2-3 секунды, затем посмотреть влево, как
можно дальше (при этом голова остается в том же положении) "и
задержать взгляд на 2-3 секунды, повторить упражнение 10 раз.
Упражнение 3.
Вращать глаза по часовой стрелке -10 раз, затем в обратную
сторону 10 раз.