Similar presentations:
Логика высказываний
1. ЛОГИКА ВЫСКАЗЫВАНИЙ
ПреподавательИванилова Татьяна Николаевна
2. Высказывания и операции над ними
3.
ОпределениеПод высказыванием понимают
языковое предложение, о котором
можно сказать, истинно оно или ложно
4.
Логические значения высказываний:«истина» (И, 1, t)
«ложь» (Л, 0, f)
5.
Примеры:1. Париж – столица Англии
2. Шесть делится на два
3. Сколько будет 7*7?
4. 7 * х = 21
Укажите высказывания и их логические
значения
6.
Высказывание, представляющее собойодно утверждение, называют простым
(элементарным).
Высказывания, которые получаются из
простых с помощью грамматических
связок:
«не», «и», «или», «если …, то …», «тогда
и только тогда, когда»
принято называть сложными
(составными)
7.
ПримерКарась не рыба
Это простое или сложное высказывание?
8.
Все высказывания будем рассматривать сточностью до их логического значения
Пример
«В Красноярске есть педагогический вуз»
«Два – простое число»
Эти высказывания для нас одинаковые
(оба истинны)
9.
Элементарные высказывания будемобозначать латинскими буквами:
А, В, С, …
x, y, z, ...
10.
Логическое значение высказыванияопределяется функцией истинности,
которая принимает значения в
двухэлементном множестве {0; 1}
11.
ОпределениеОтрицанием высказывания А называется
новое высказывание, которое является
истинным, если А – ложно, и ложным,
если А – истинно
Обозначение:
Читается: «не А», «Неверно, что А»
12.
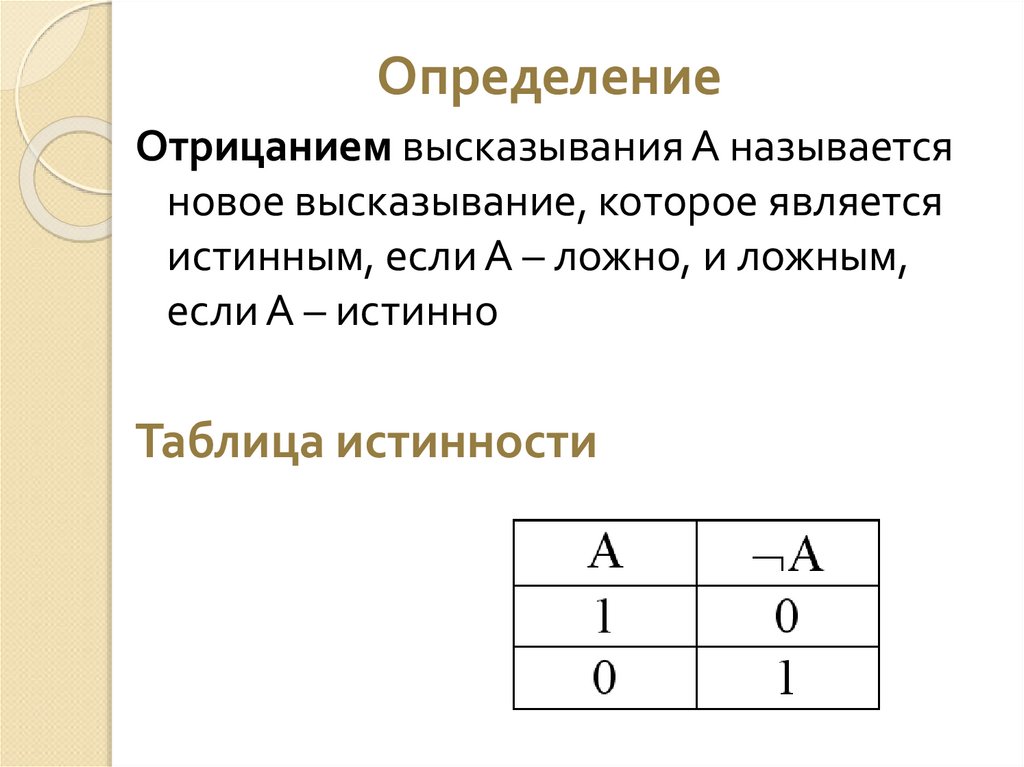
ОпределениеОтрицанием высказывания А называется
новое высказывание, которое является
истинным, если А – ложно, и ложным,
если А – истинно
Таблица истинности
13.
ОпределениеКонъюнкцией двух высказываний А, В
называется новое высказывание,
которое является истинным в
единственном случае, если оба
высказывания А, В – истинны
Обозначение:
Читается: «А и В»
14.
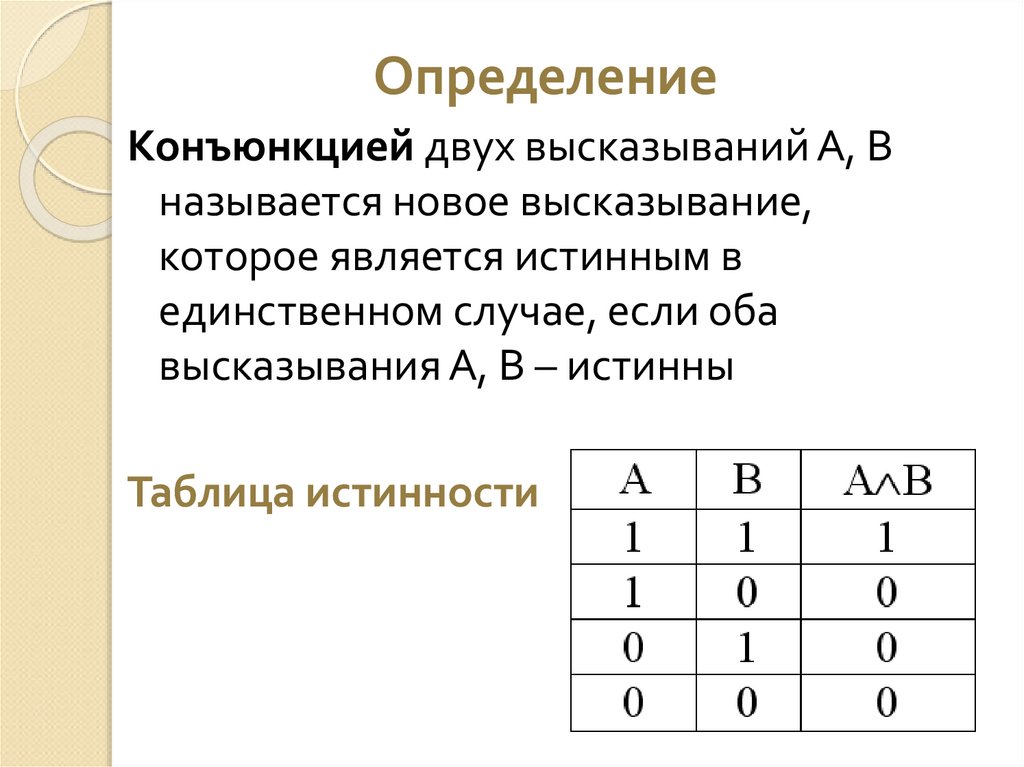
ОпределениеКонъюнкцией двух высказываний А, В
называется новое высказывание,
которое является истинным в
единственном случае, если оба
высказывания А, В – истинны
Таблица истинности
15.
Конъюнкция: логическое умножение АВТаблица истинности
16.
ОпределениеДизъюнкцией двух высказываний А, В
называется новое высказывание,
которое является ложным в
единственном случае, если оба
высказывания А, В – ложны
Обозначение:
Читается: «А или В»
17.
ОпределениеДизъюнкцией двух высказываний А, В
называется новое высказывание,
которое является ложным в
единственном случае, если оба
высказывания А, В – ложны
Таблица истинности
18.
ОпределениеИмпликацией двух высказываний А, В
называется новое высказывание,
которое является ложным в
единственном случае, если первое
высказывание А - истинно, а второе
высказывание В – ложно
19.
ИмпликацияОбозначение:
Читается:
«если А, то В»
«из А следует В»
«А имплицирует В»
А – посылка
В – заключение
20.
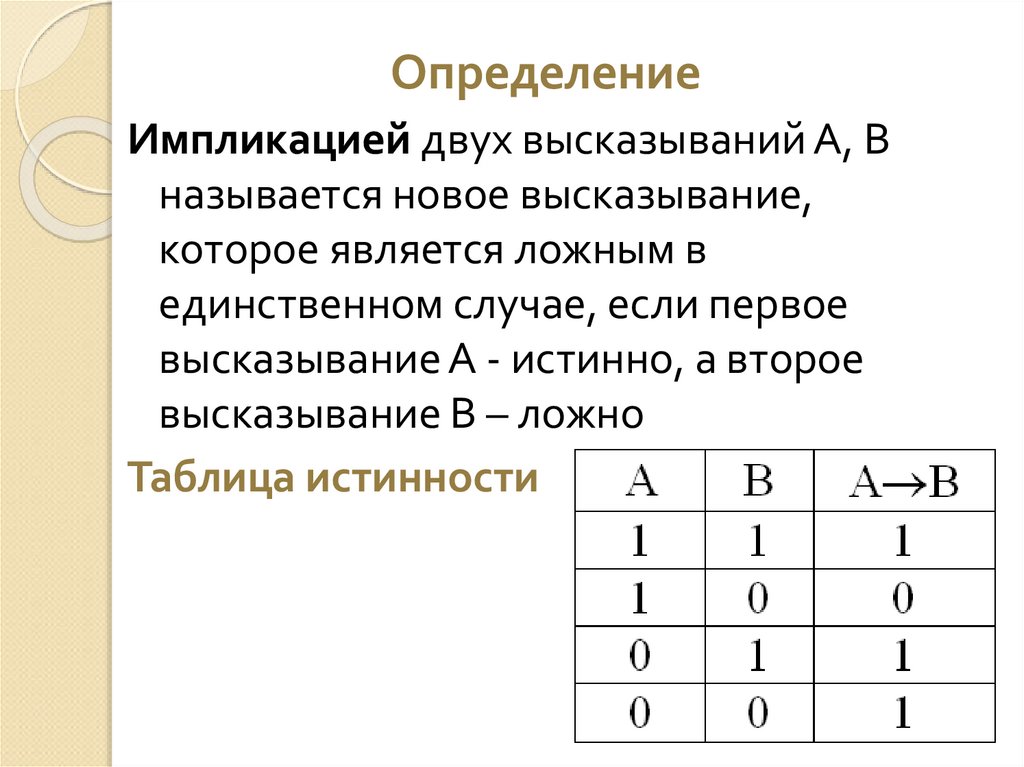
ОпределениеИмпликацией двух высказываний А, В
называется новое высказывание,
которое является ложным в
единственном случае, если первое
высказывание А - истинно, а второе
высказывание В – ложно
Таблица истинности
21.
ОпределениеЭквивалентностью двух высказываний А,
В называется новое высказывание,
которое является истинным, если
высказывания А, В имеют одинаковые
логические значения, и ложным – в
остальных случаях
22.
ЭквивалентностьОбозначение: A~B,
Читается:
- «А тогда и только тогда, когда В»
- «для того, чтобы А, необходимо и
достаточно, чтобы В»
- «А эквивалентно В»
23.
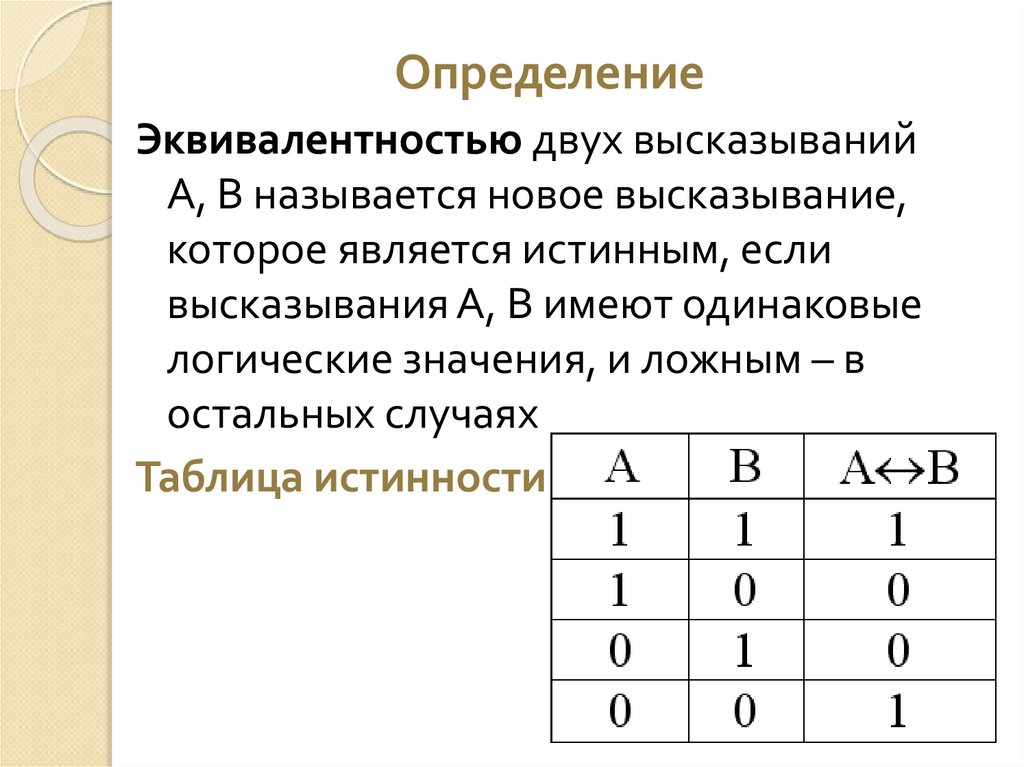
ОпределениеЭквивалентностью двух высказываний
А, В называется новое высказывание,
которое является истинным, если
высказывания А, В имеют одинаковые
логические значения, и ложным – в
остальных случаях
Таблица истинности
24.
Разделительное «или»Обозначение:A B
Читается:
- «А не эквивалентно В»
- Операция “XOR”
25.
ОпределениеРазделительное «или» для двух
высказываний А, В это новое
высказывание, которое истинно, если
высказывания А, В имеют разные
логические значения, и ложно – в
остальных случаях.
A B ( A B)
26. Дополнительные связки
Штрих ШеффераA |B A B
Стрелка Пирса(функция Вебба)
A B A B
27. Таблицы истинности
Составляются для любой формулы логикивысказываний
Если в формуле n переменных, то в таблице
строк 2n
Пусть дана формула F(x1,x2,…,xn)
Список переменных формулы <x1,x2,…,xn>
Оценки списка переменных
<0,0,…,0>,<0,1,…,1>, <1,1,0,…,1>, <1,1,…,1>
и т.п.
28.
•Для формулы, которая содержит двепеременные, таких наборов значений
переменных всего четыре: (0,0), (0,1), (1,0),
(1,1).
•Если формула содержит три переменные, то
возможных наборов значений переменных
восемь:
•(0,0,0), (0,0,1), (0,1,0), (0,1,1),
•(1,0,0), (1,0,1), (1,1,0), (1,1,1).
•Количество наборов для формулы с четырьмя
переменными равно шестнадцати и т.д.
29. Основные законы алгебры логики
ЗаконДля И
Для ИЛИ
Коммутативность
А В В А
А В В А
Дистрибутивность
А (В С) (А В) (А С)
А (В С) (А В) (А С)
Идемпотентность
А А А
А А А
Ассоциативность
А (В С) (А В) С
А (В С) (А В) С
Закон де Моргана
(А В) А В
(А В) А В
Закон
расщепления
А (А В) (А В)
А (А В) (А В)
Закон поглощения
А (А В) А
А (А В) А
Снятие
двойного
отрицания
А А
30. Выражение одних логических связок через другие:
А В А В (А В)А В (А В) (В А) ( A B) ( B A)
(А В) ( А В)
А В А В ( А В)
А В (А В) ( ( А В))
А В (А В) =(А В) ( А В)
31. Тавтология
Некоторые формулы принимаютзначение “истина” при любых
значениях истинности входящих в них
переменных. Например, формула А v
Такие формулы называются
тождественно истинными формулами
или тавтологиями.
Высказывания, которые
формализуются тавтологиями,
называются логически истинными
высказываниями.
32. Тождественная ложь
В качестве другого примера рассмотрим формулу А &, которой соответствует, например, высказывание
“Катя самая высокая девочка в классе, и в классе есть
девочки выше Кати”. Очевидно, что эта формула
ложна, так как либо А, либо обязательно ложно.
Такие формулы называются тождественно ложными
формулами или противоречиями.
Высказывания, которые формализуются
противоречиями, называются логически ложными
высказываниями.
33. Тождественная ложь
При всех наборах значений переменных x и y формулапринимает значение 0, то есть является тождественно
ложной.
34. Выполнимая формула
Формула в некоторых случаях принимает значение 1, а внекоторых — 0, то есть является выполнимой.






























 mathematics
mathematics








