Similar presentations:
Типовые динамические звенья. Математические модели, примеры, характеристики
1.
Типовые динамические звеньяматематические модели, примеры, характеристики.
2.
Пропорциональное (безынерционное) звено.Уравнение (оригинал):
xВЫХ kxВХ
Передаточная функция:
X ВЫХ
W
k
X ВХ
L( ) 20 lg k
3.
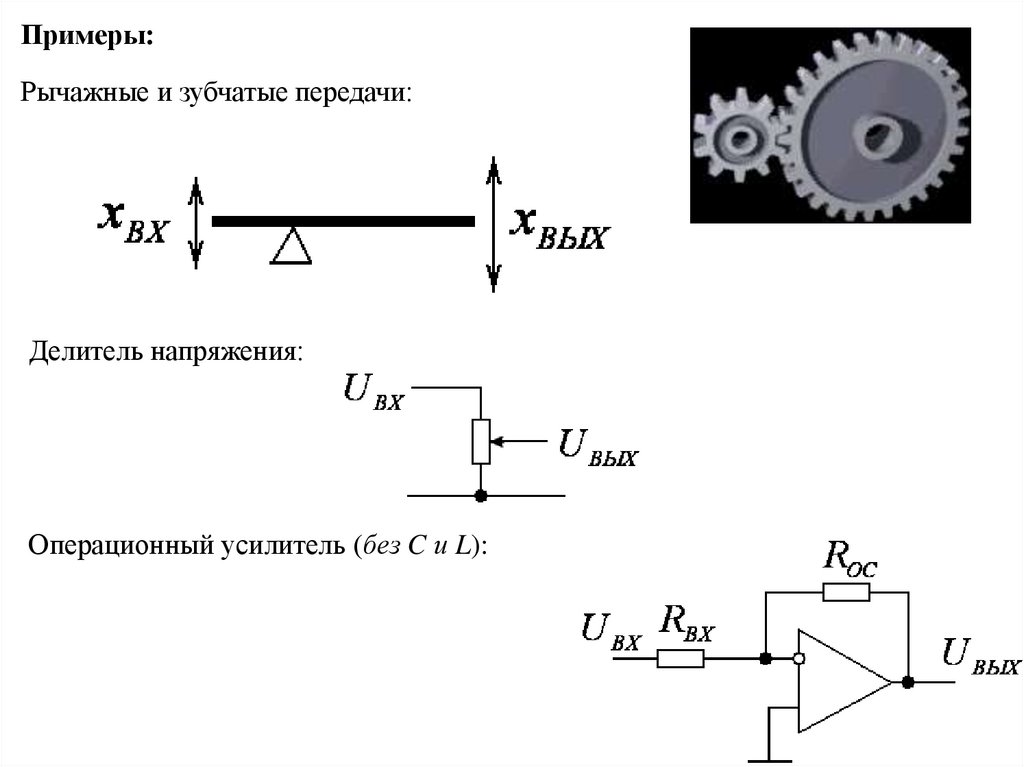
Примеры:Рычажные и зубчатые передачи:
Делитель напряжения:
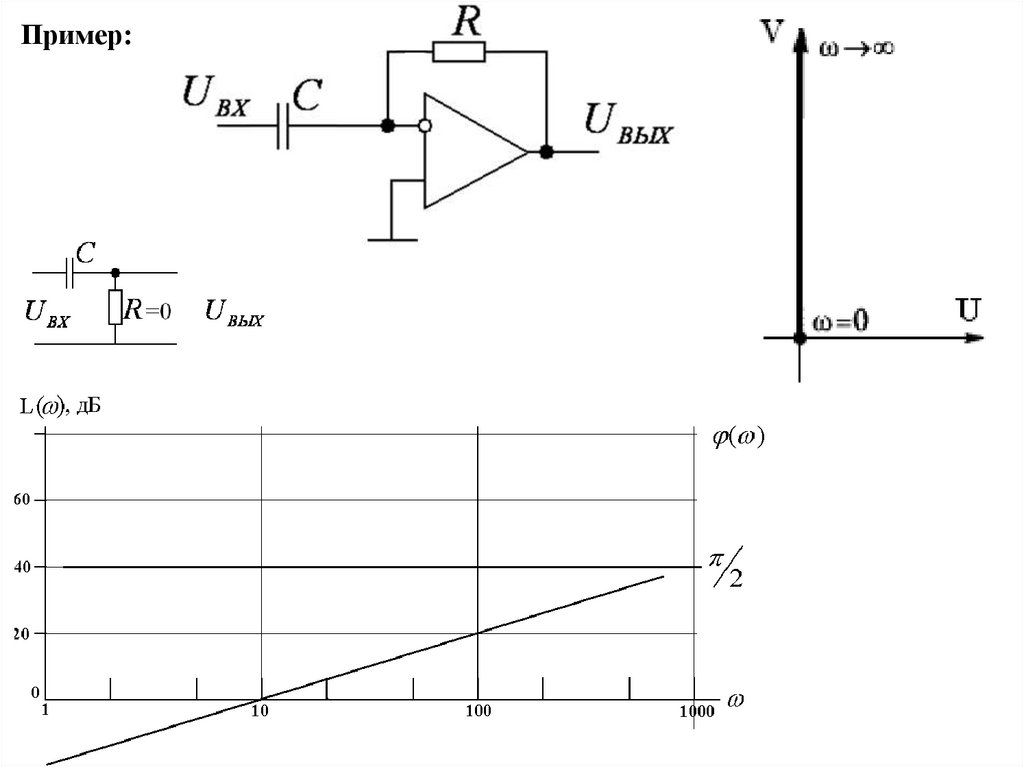
Операционный усилитель (без C и L):
4.
Интегрирующее звено.Дифференциальное уравнение (оригинал):
Операторная форма (изображение):
TpX ВЫХ X ВХ
X ВЫХ
1
k
W
X ВХ
Tp p
1
W (i )
i T
dxВЫХ
T
xВХ
dt
5.
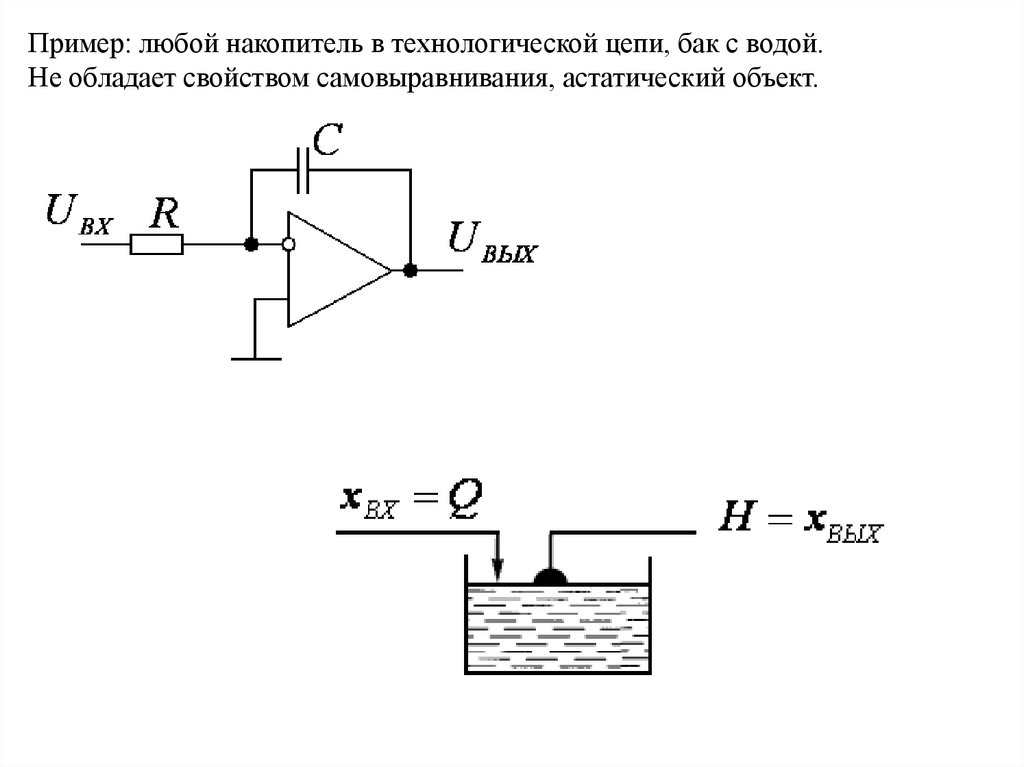
Пример: любой накопитель в технологической цепи, бак с водой.Не обладает свойством самовыравнивания, астатический объект.
6.
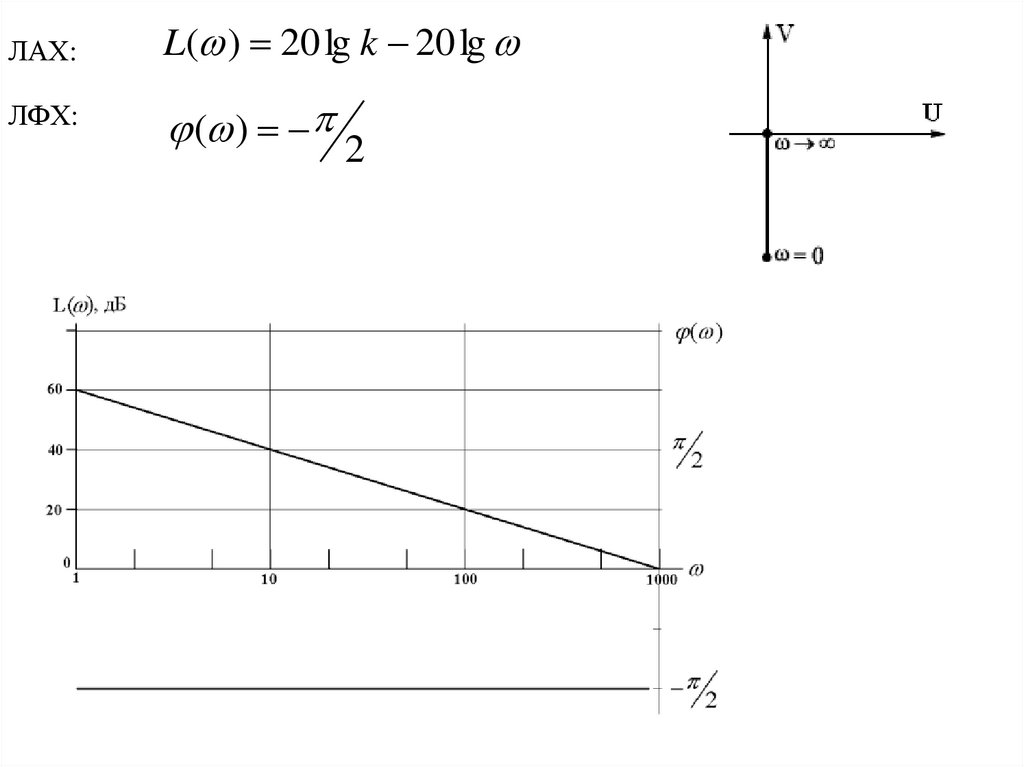
ЛАХ:ЛФХ:
L( ) 20 lg k 20 lg
( ) 2
7.
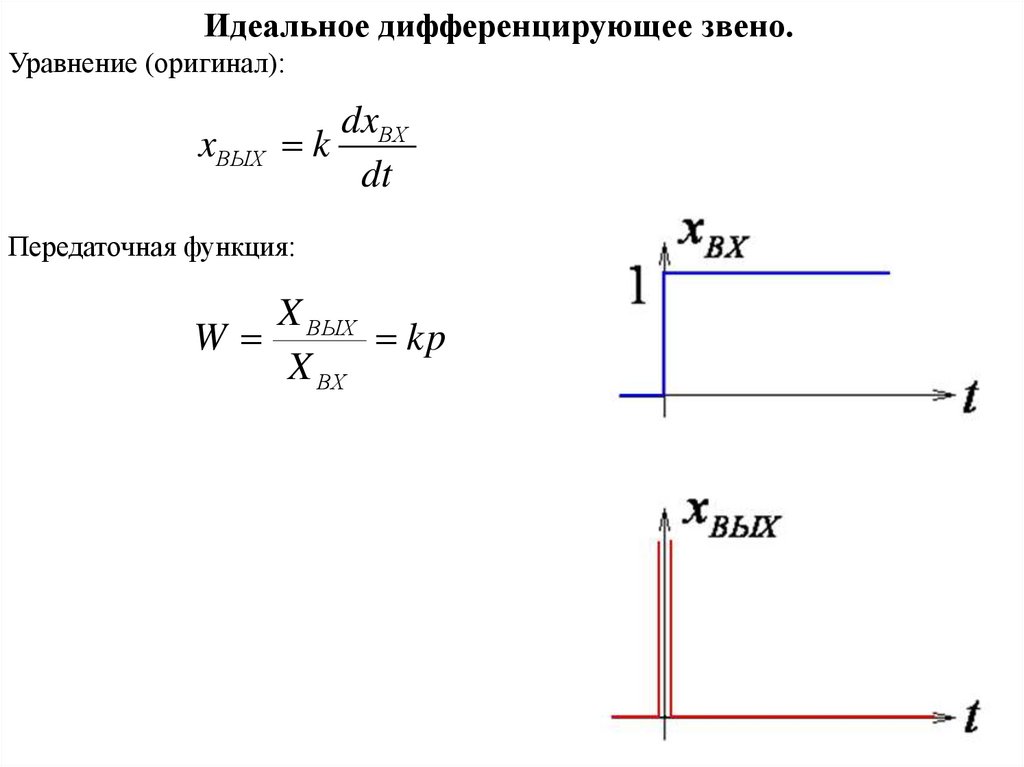
Идеальное дифференцирующее звено.Уравнение (оригинал):
dxВХ
xВЫХ k
dt
Передаточная функция:
X ВЫХ
W
kp
X ВХ
8.
Пример:9.
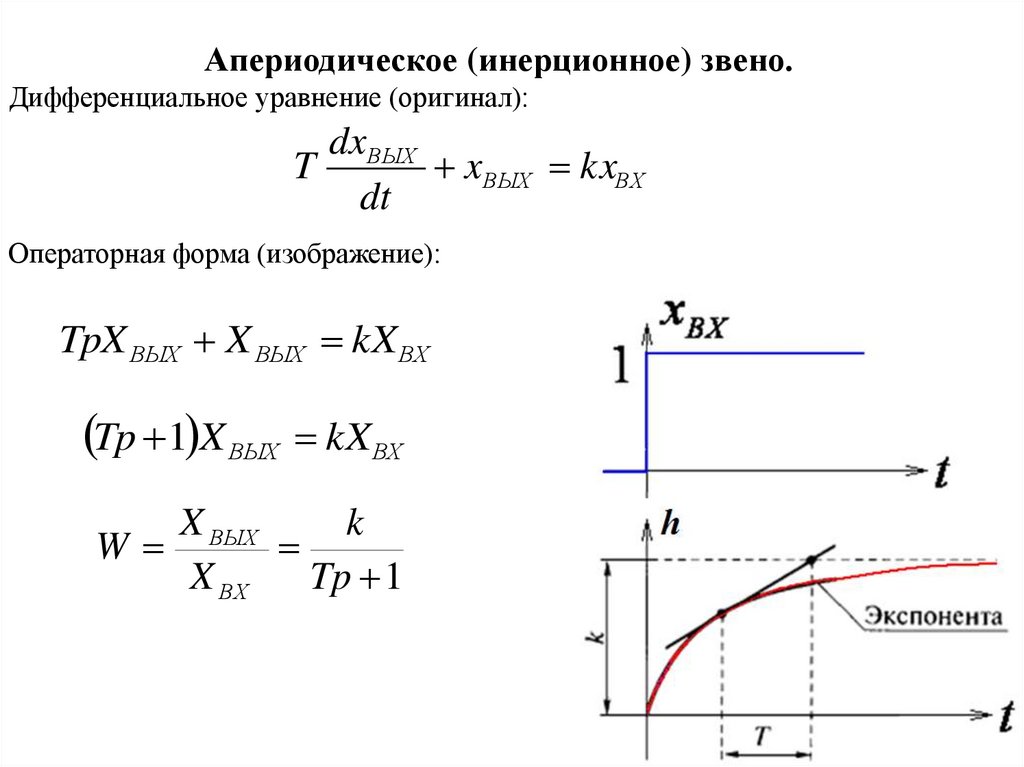
Апериодическое (инерционное) звено.Дифференциальное уравнение (оригинал):
dxВЫХ
T
xВЫХ kxВХ
dt
Операторная форма (изображение):
TpX ВЫХ X ВЫХ kX ВХ
Tp 1 X ВЫХ kXВХ
X ВЫХ
k
W
X ВХ
Tp 1
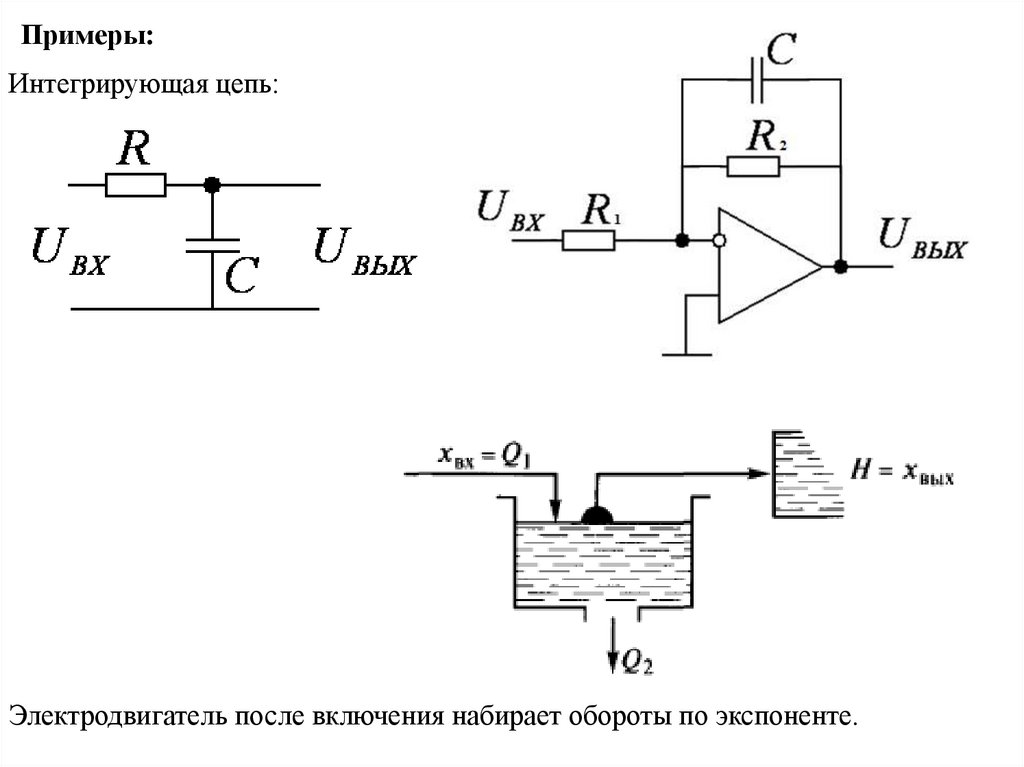
10.
Примеры:Интегрирующая цепь:
Электродвигатель после включения набирает обороты по экспоненте.
11.
kW ( i )
i T 1
АЧХ получаем заменой p → iω
Для получения ЛАХ прологарифмируем W(ω):
L( ) 20 lg k 20 lg 2T 2 1
( ) arctg ( T )
Рассмотрим вторую составляющую ЛАХ:
L2 ( ) 20 lg T 1
2
2
При ωТ << 1, L2(ω) = 0,
При ωT >> 1, L2(ω) = -20lg(ωT).
Логарифмическую амплитудную характеристику можно представить в виде двух
асимптот (прямых), сопряженных в точке ωS = 1/T. В окрестности ωS асимптоты
сопрягаются плавной кривой, лежащей ниже точки сопряжения на 3 дБ.
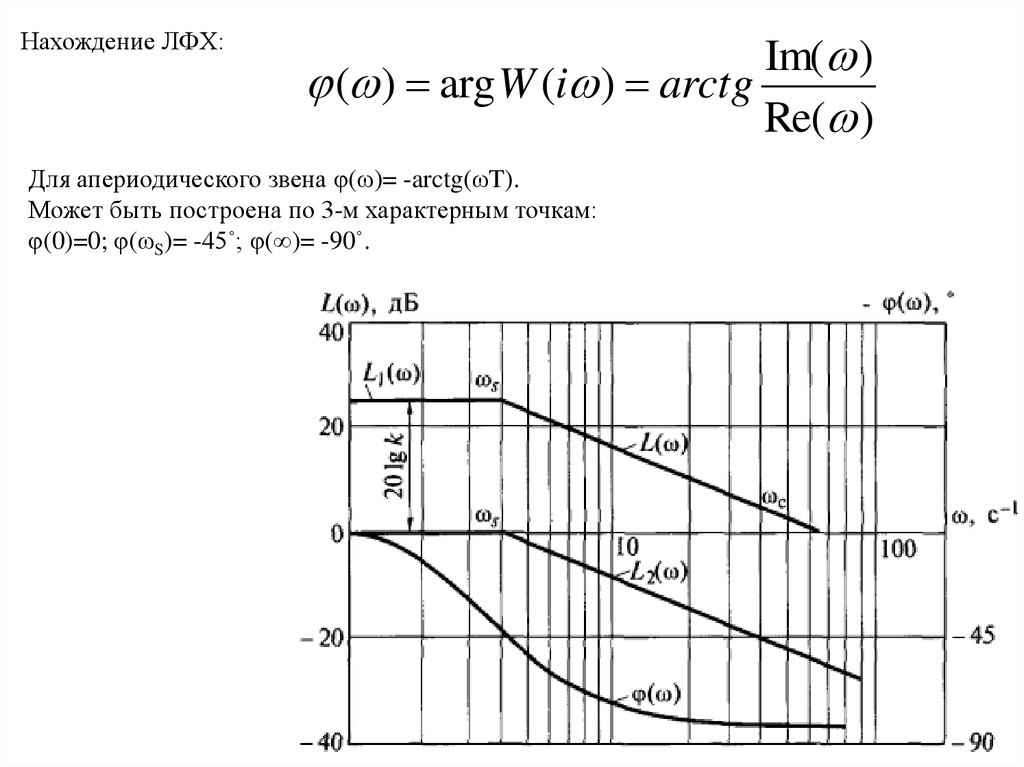
12.
Нахождение ЛФХ:Im( )
( ) arg W (i ) arctg
Re( )
Для апериодического звена φ(ω)= -arctg(ωT).
Может быть построена по 3-м характерным точкам:
φ(0)=0; φ(ωS)= -45˚; φ(∞)= -90˚.
13.
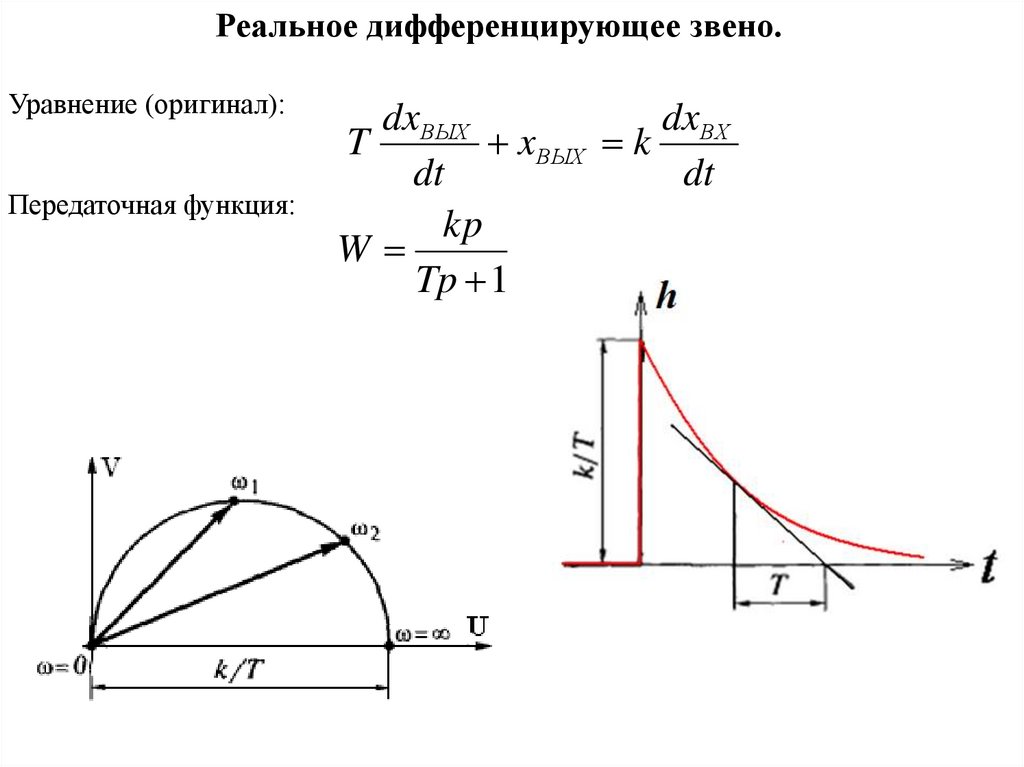
Реальное дифференцирующее звено.Уравнение (оригинал):
Передаточная функция:
dxВЫХ
dxВХ
T
xВЫХ k
dt
dt
kp
W
Tp 1
14.
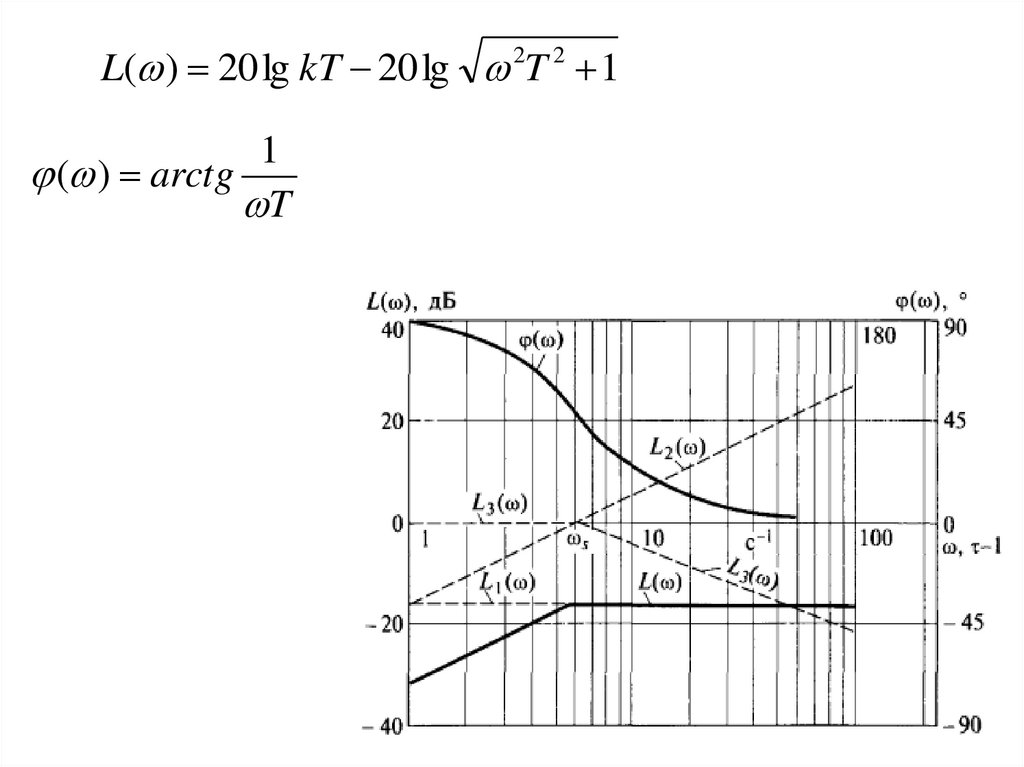
L( ) 20 lg kT 20 lg 2T 2 11
( ) arctg
T
15.
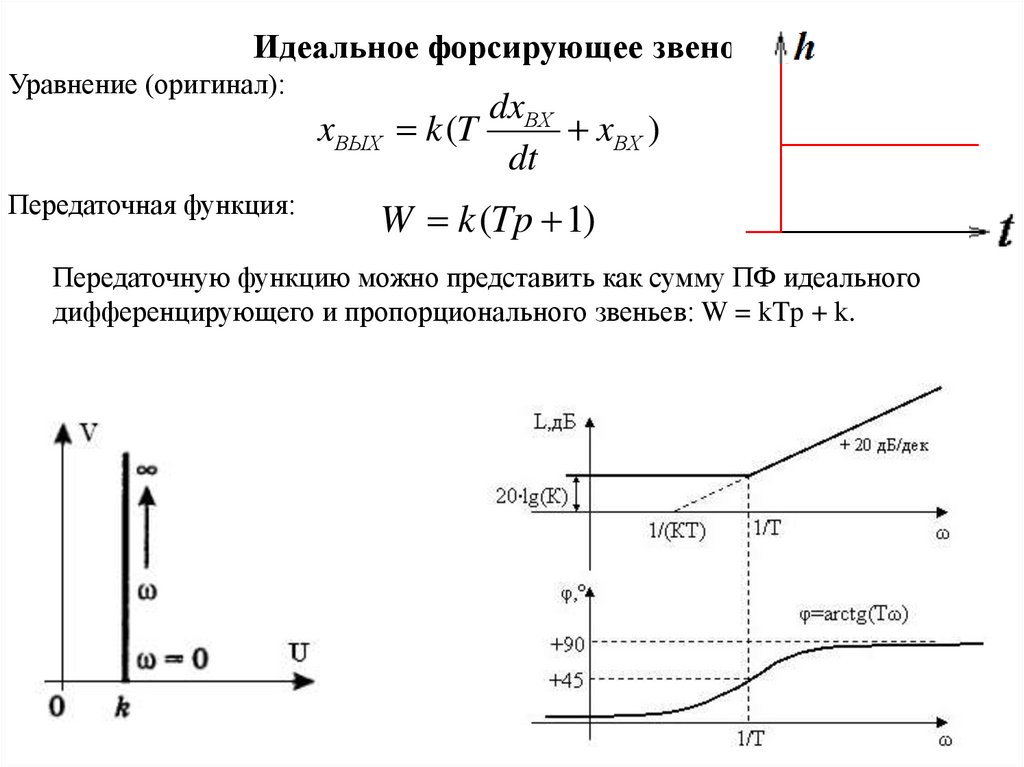
Идеальное форсирующее звено.Уравнение (оригинал):
Передаточная функция:
dxВХ
xВЫХ k (T
xВХ )
dt
W k (Tp 1)
Передаточную функцию можно представить как сумму ПФ идеального
дифференцирующего и пропорционального звеньев: W = kTp + k.
16.
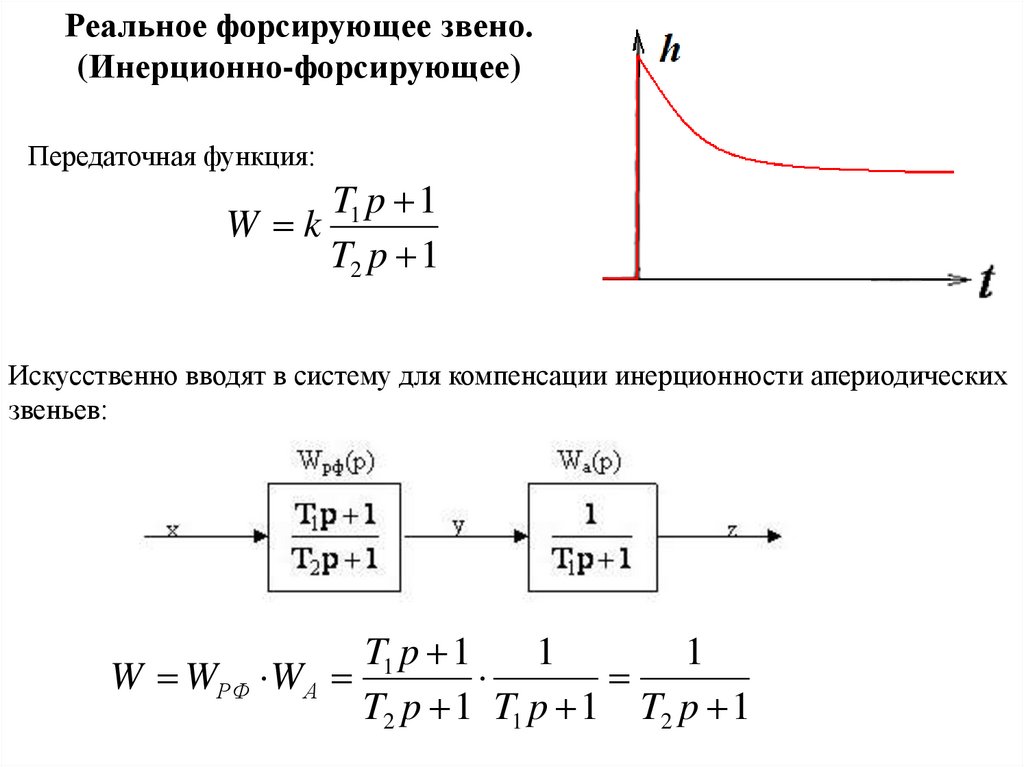
Реальное форсирующее звено.(Инерционно-форсирующее)
Передаточная функция:
T1 p 1
W k
T2 p 1
Искусственно вводят в систему для компенсации инерционности апериодических
звеньев:
T1 p 1
1
1
W WРФ WА
T2 p 1 T1 p 1 T2 p 1
17.
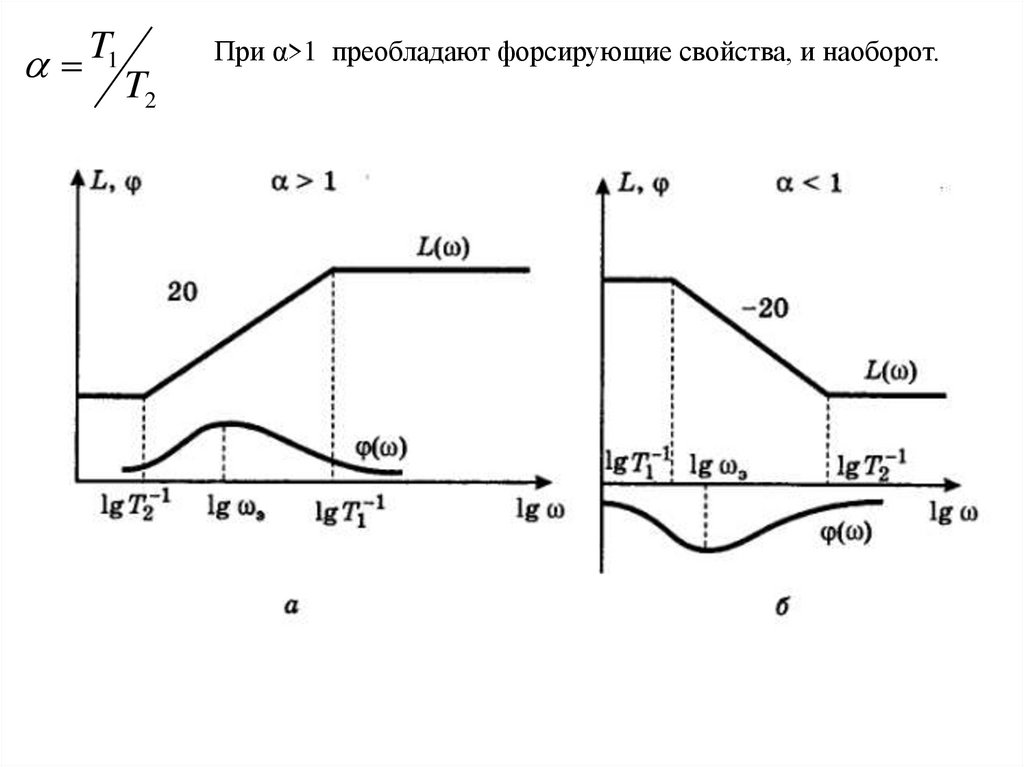
T1 T2
При α>1 преобладают форсирующие свойства, и наоборот.
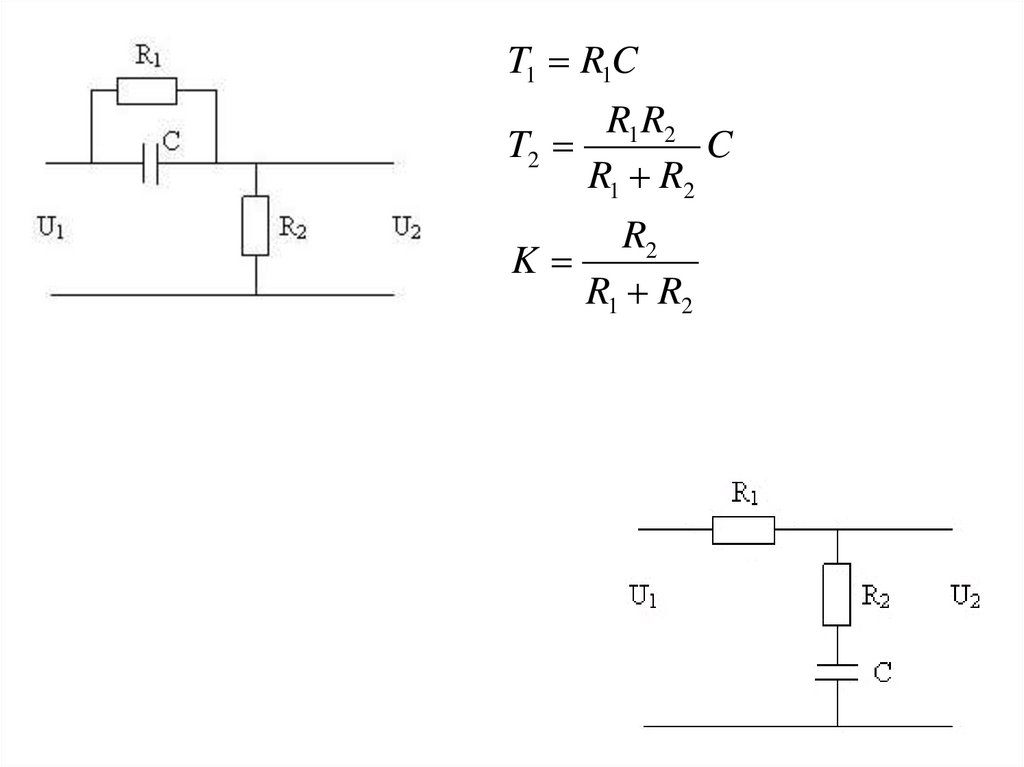
18.
T1 R1CR1 R2
T2
C
R1 R2
R2
K
R1 R2
19.
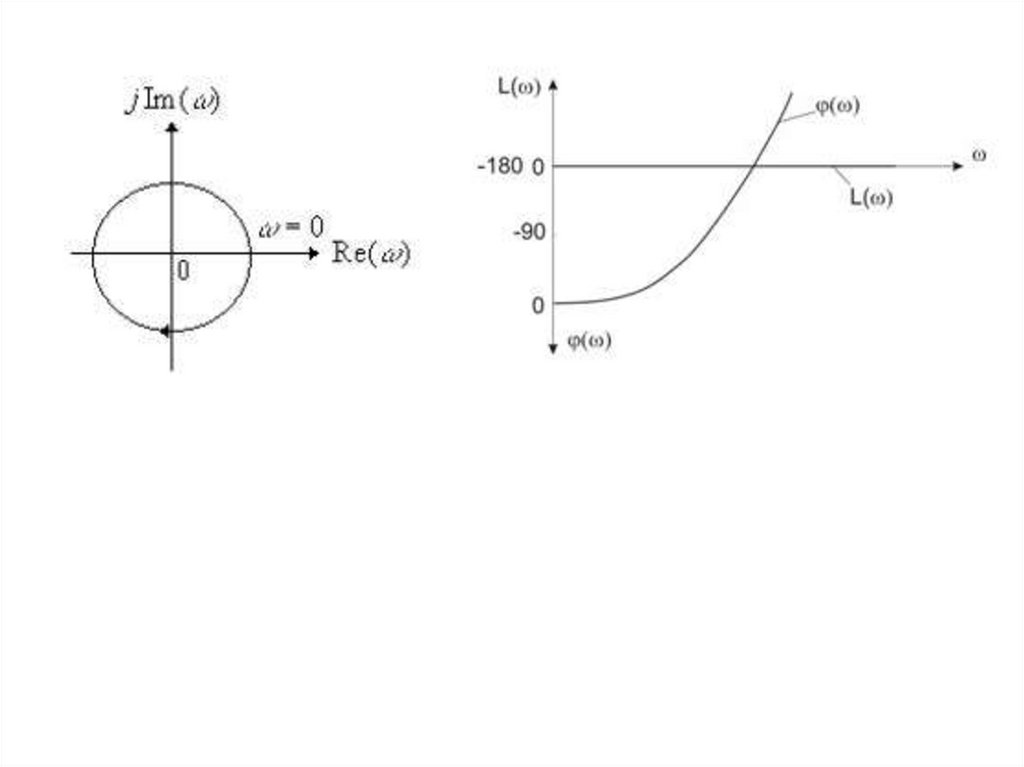
Звено чистого запаздывания (транспортное)Уравнение (оригинал):
Передаточная функция:
xВЫХ (t ЗАП ) xВХ (t )
W exp( p ЗАП )
L( ) 20 lg 1 0
( ) ЗАП
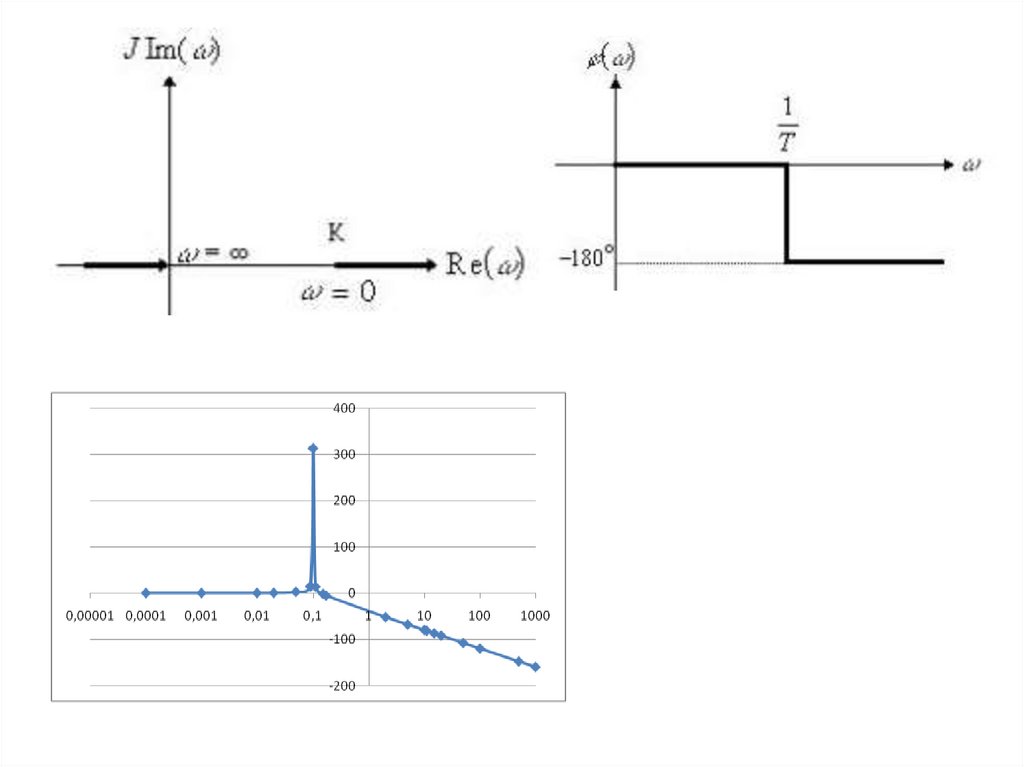
20.
21.
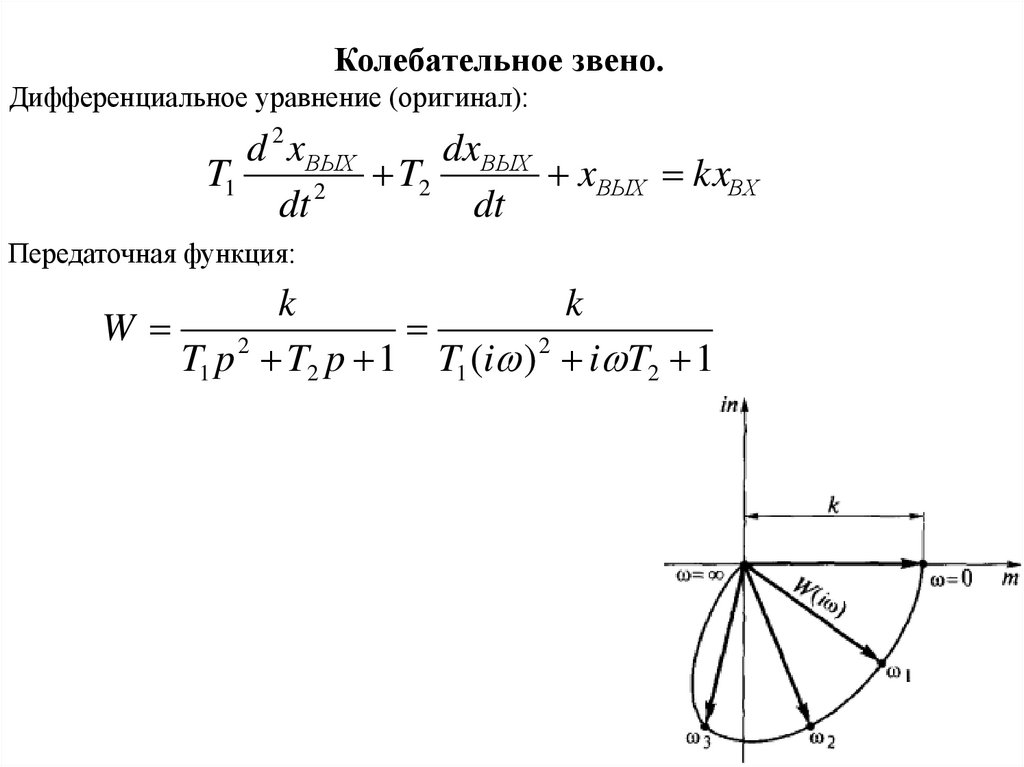
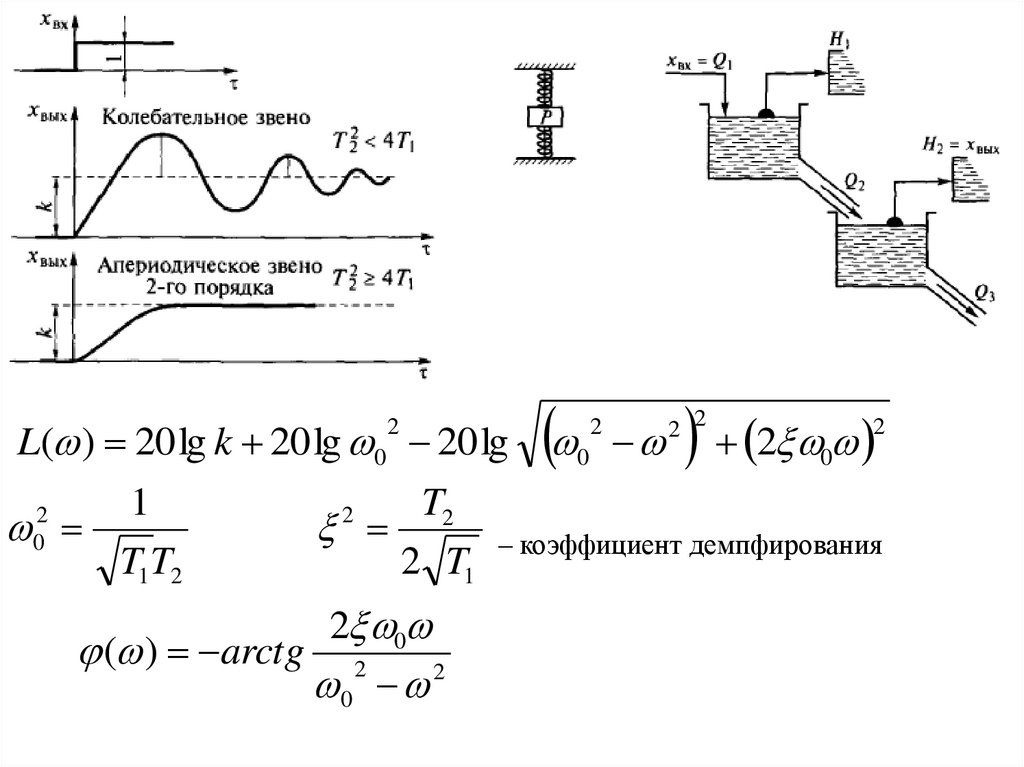
Колебательное звено.Дифференциальное уравнение (оригинал):
d 2 xВЫХ
dxВЫХ
T1
T2
xВЫХ kxВХ
2
dt
dt
Передаточная функция:
k
k
W
2
T1 p T2 p 1 T1 (i ) 2 i T2 1
22.
L( ) 20 lg k 20 lg 0 20 lg2
1
T1T2
2
0
2
2
0
2 2
2
0
T2
2 T1 – коэффициент демпфирования
2
2 0
( ) arctg 2
0 2
23.
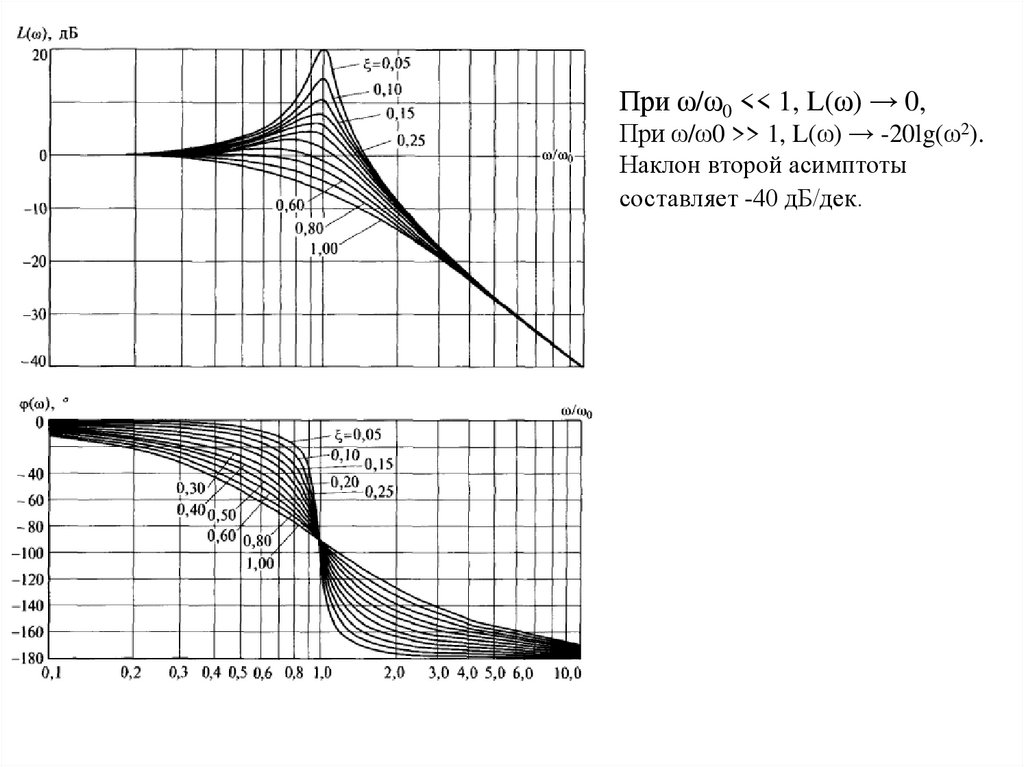
При ω/ω0 << 1, L(ω) → 0,При ω/ω0 >> 1, L(ω) → -20lg(ω2).
Наклон второй асимптоты
составляет -40 дБ/дек.
24.
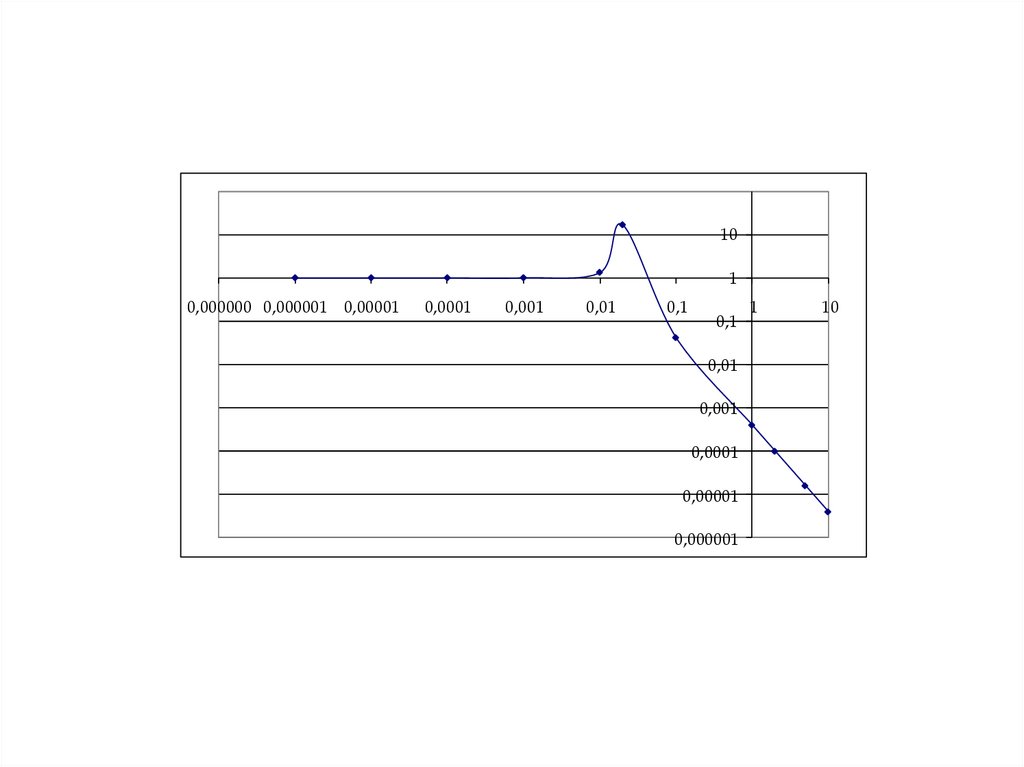
При 0,38 < ξ < 0,707 расхождение между асимптотической и истинной ЛАЧХ непревышает 3 дБ, при меньших значениях ξ асимптотическую ЛАЧХ корректируют
на величину выброса h. Значение h находят по приблизительной формуле
1 l
h 20 lg
2 2
где l – число одинаковых корней (кратность корня),
или по типовым характеристикам.
ξ
0,05
0,1
0,15
0,3
0,6
1
h, дБ
20
14
10
5
0
-5
25.
101
0,000000 0,000001
0,00001
0,0001
0,001
0,01
0,1
0,1
0,01
0,001
0,0001
0,00001
0,000001
1
10
26.
Консервативное звено.Дифференциальное уравнение (оригинал):
d 2 xВЫХ
T
xВЫХ kxВХ
2
dt
Передаточная функция:
W
k
Tp 2 1
27.
28.
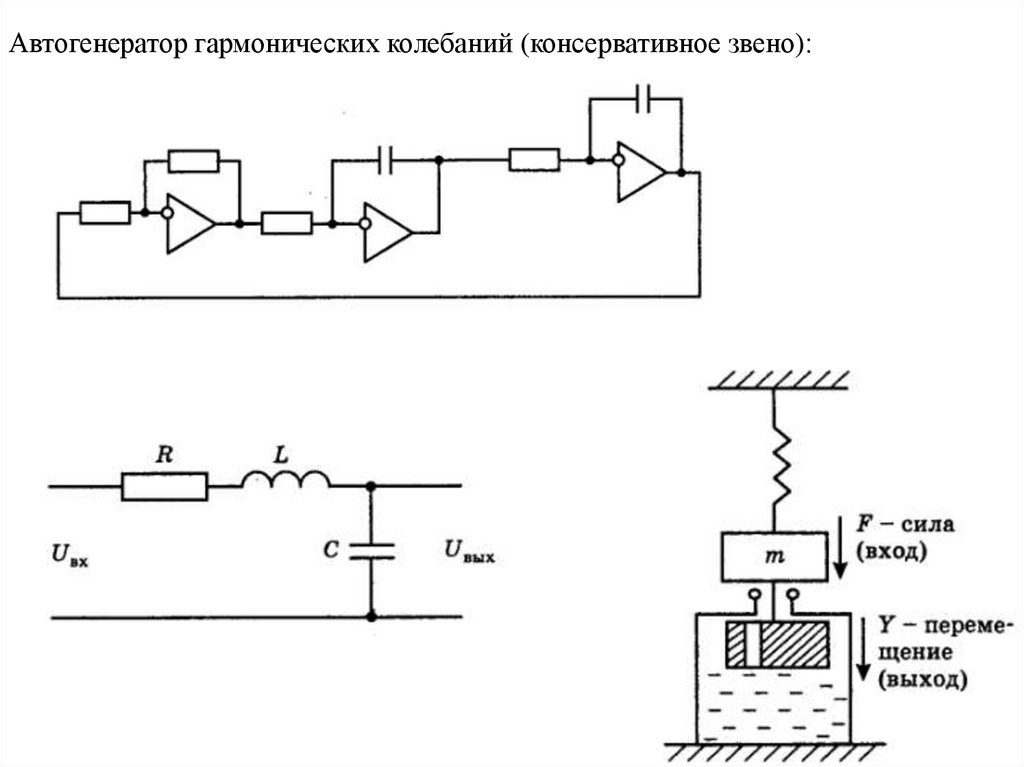
Автогенератор гармонических колебаний (консервативное звено):29.
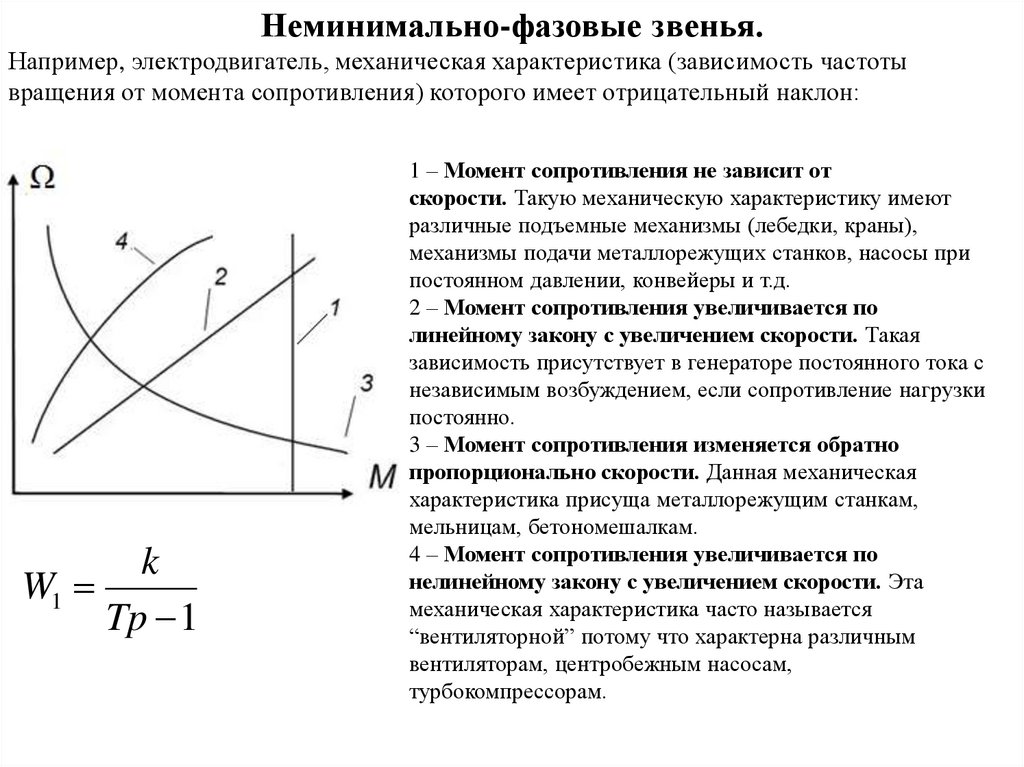
Неминимально-фазовые звенья.Например, электродвигатель, механическая характеристика (зависимость частоты
вращения от момента cопротивления) которого имеет отрицательный наклон:
k
W1
Tp 1
1 – Момент сопротивления не зависит от
скорости. Такую механическую характеристику имеют
различные подъемные механизмы (лебедки, краны),
механизмы подачи металлорежущих станков, насосы при
постоянном давлении, конвейеры и т.д.
2 – Момент сопротивления увеличивается по
линейному закону с увеличением скорости. Такая
зависимость присутствует в генераторе постоянного тока с
независимым возбуждением, если сопротивление нагрузки
постоянно.
3 – Момент сопротивления изменяется обратно
пропорционально скорости. Данная механическая
характеристика присуща металлорежущим станкам,
мельницам, бетономешалкам.
4 – Момент сопротивления увеличивается по
нелинейному закону с увеличением скорости. Эта
механическая характеристика часто называется
“вентиляторной” потому что характерна различным
вентиляторам, центробежным насосам,
турбокомпрессорам.
30.
kW
1 T 2 p2
k
W
1 2 Tp T 2 p 2
Квазиконсервативное звено:
Квазиколебательное звено:
Колебательное звено с
отрицательным затуханием:
k
W
1 2 Tp T 2 p 2
T1 p 1
W k
T2 p 1
и другие….








 mathematics
mathematics








