Similar presentations:
Сжатие и помехоустойчивое кодирование. Практическое занятие 5. Циклический код Хемминга, CRC
1.
Центр дистанционного обученияСжатие и помехоустойчивое кодирование
Практическое занятие 5
Циклический код Хемминга, CRC
ФИО преподавателя: Смирнов
Александр Витальевич
e-mail: av_smirnov@mirea.ru
online.mirea.ru
2. Введение
Центр дистанционного обученияВведение
1. Выполнение заданий по данной теме рассчитано на два
практических занятия. По теме оформляется отчет в
электронном виде. Рекомендуемый формат файла .pdf. Имя
файла должно содержать сокращенное название дисциплины,
фамилию студента, номер группы и номер работы. Текст и
таблицы отчета могут выполняться как на компьютере, так и на
бумаге с последующим сканированием или
фотографированием.
online.mirea.ru
3. П2. Ответы на вопросы
Центр дистанционного обученияП2. Ответы на вопросы
2.1. Дать определение циклического кода.
2.2. Дать определение порождающего многочлена.
2.3. Указать основные свойства кодов Хемминга: минимальное
расстояние, исправляющую способность, скорость, разрядность
синдрома.
2.4. Каковы возможности кодов Хемминга в режимах исправления и
обнаружения ошибок?
2.5. Дать определение расширенного кода.
2.6. Указать основное назначение кодов CRC.
2.7. Какие ошибки можно обнаруживать с помощью кодов CRC?
2.8. Сколько разных значений может иметь контрольная сумма CRC,
если степень порождающего полинома равна m?
2.9. Приведите два примера систем, в которых используются коды
CRC, укажите типы этих кодов и разрядность их порождающих
многочленов.
online.mirea.ru
4. Пункты 3.1 и 3.2
Центр дистанционного обученияПункты 3.1 и 3.2
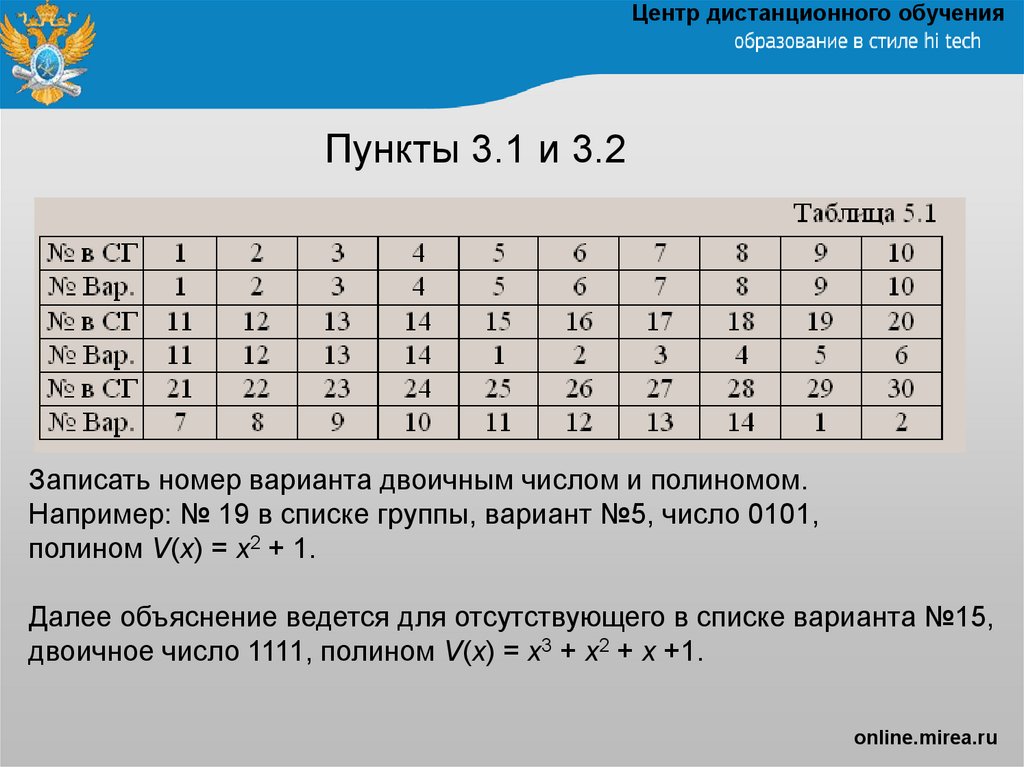
Записать номер варианта двоичным числом и полиномом.
Например: № 19 в списке группы, вариант №5, число 0101,
полином V(x) = x2 + 1.
Далее объяснение ведется для отсутствующего в списке варианта №15,
двоичное число 1111, полином V(x) = x3 + x2 + x +1.
online.mirea.ru
5. Пункты 3.3 и 3.4
Центр дистанционного обученияПункты 3.3 и 3.4
3.3. Найти кодовое слово W(x), умножив полином V(x) на
порождающий полином g(x) = x3 + x + 1.
W(x) = V(x) g(x) = (x3 + x2 + x +1)(x3 + x + 1) = x6 + x5 + x4 + x3 + x4 + x3 +
+ x2 + x + x3 + x2 + x +1 = x6 + x5 + x3 + 1. Число 1101001.
3.4. Поделить полученное кодовое слово W(x) «в столбик» на
порождающий полином, убедиться, что получается полином V(x).
online.mirea.ru
6. Пункт 3.4. Окончание
Центр дистанционного обученияПункт 3.4. Окончание
Ввести в W(x) одну ошибку. Поделить на g(x), убедиться, что
получается остаток от деления.
В число 1101001 введем одну ошибку: 1101000.
Многочлен W'(x) = x6 + x5 + x3 . Выполняем деление:
online.mirea.ru
7. Пункт 4.1
Центр дистанционного обученияПункт 4.1
Найти кодовое слово Ws(x) систематического кода. Четыре
старших бита Ws(x) являются битами V(x), а три младших - остаток
от деления x3V(x) на g(x).
Запишем x3V(x) = x6 + x5 + x4 + x3. Выполним деление
Частное от деления затем не используется. Остаток равен x2+x+1.
Таким образом, получаем кодовое слово
Ws(x) = x6 + x5 + x4 + x3 + x2 + x + 1.
online.mirea.ru
8. Пункт 4.2
Центр дистанционного обученияПункт 4.2
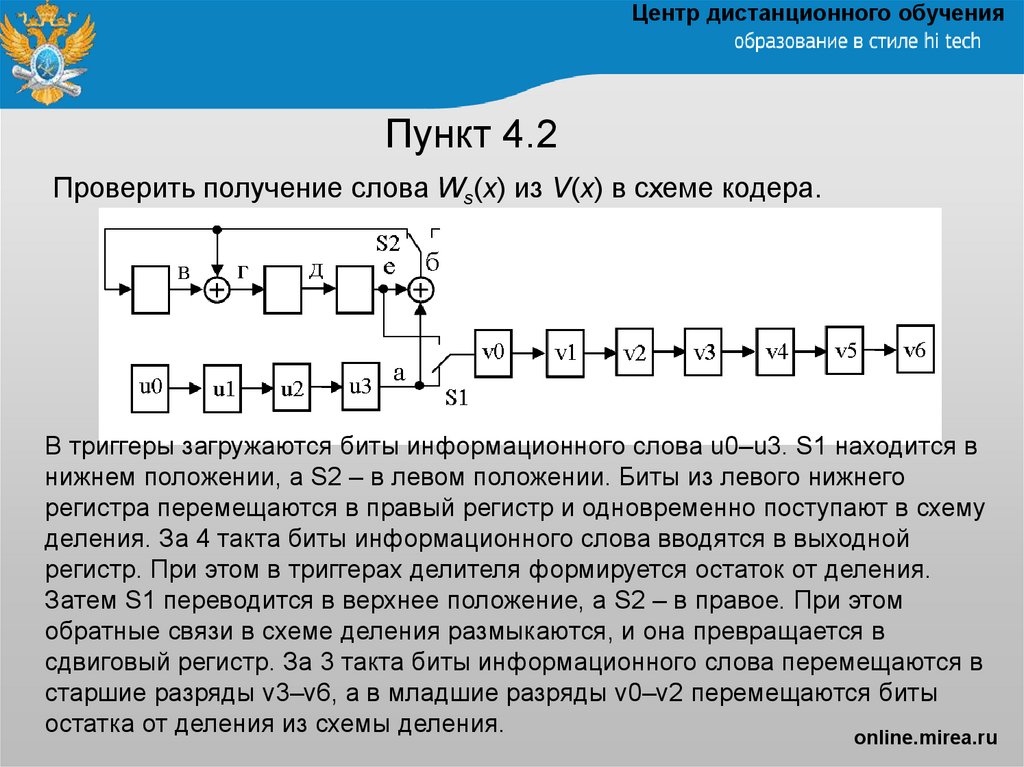
Проверить получение слова Ws(x) из V(x) в схеме кодера.
В триггеры загружаются биты информационного слова u0–u3. S1 находится в
нижнем положении, а S2 – в левом положении. Биты из левого нижнего
регистра перемещаются в правый регистр и одновременно поступают в схему
деления. За 4 такта биты информационного слова вводятся в выходной
регистр. При этом в триггерах делителя формируется остаток от деления.
Затем S1 переводится в верхнее положение, а S2 – в правое. При этом
обратные связи в схеме деления размыкаются, и она превращается в
сдвиговый регистр. За 3 такта биты информационного слова перемещаются в
старшие разряды v3–v6, а в младшие разряды v0–v2 перемещаются биты
остатка от деления из схемы деления.
online.mirea.ru
9. Пункт 4.2. Окончание
Центр дистанционного обученияПункт 4.2. Окончание
Выходы сумматоров:
«б» = «а»+«е»; «г» = «б»+«в».
В табл. 5.2 каждая строка соответствует
состоянию после подачи тактового
импульса, когда триггеры перешли в
новые состояния, и на выходах
сумматоров также установились новые
состояния.
Триггеры с выходами «в», «д», «е» предварительно установлены в нули.
Слово 1111 подается в точку «а», начиная со старшего бита. На выходах
сумматоров "1". По первому тактовому импульсу в триггер «а» записывается
второй, считая от старшего, бит информационного слова. Одновременно
выходное состояние сумматора «б» записывается в триггер «в», а выходное
состояние сумматора «г» записывается в триггер «д», состояние которого
записывается в триггер «е». При получении состояний триггеров в строке 1
используются выходные уровни сумматоров из строки 0 и т.д.
После 4-го тактового импульса переключатель S2 размыкается, на верхнем
входе сумматора «г» фиксируется «0», и состояния «а» и «б» не влияют на
«г». В триггерах «в», «д», «е» получается остаток от деления.
online.mirea.ru
10. Пункт 4.3
Центр дистанционного обученияПункт 4.3
Генерировать таблицу синдромов ошибок, находя синдром
каждой возможной одиночной ошибки (всего их 7), как остаток от
деления соответствующего полинома ошибки на порождающий
полином g(x).
Полиномы ошибок: e0(x) = 1; e1(x) = x; ... e6(x) = x6.
Очевидно, синдромы ошибок e0(x), e1(x), e2(x) равны самим
полиномам этих ошибок.
Для примера найдем еще синдром для ошибки e6(x).
Этот синдром равен x2 + 1. Аналогично находятся остальные.
online.mirea.ru
11. Пункты 4.4 и 4.5
Центр дистанционного обученияПункты 4.4 и 4.5
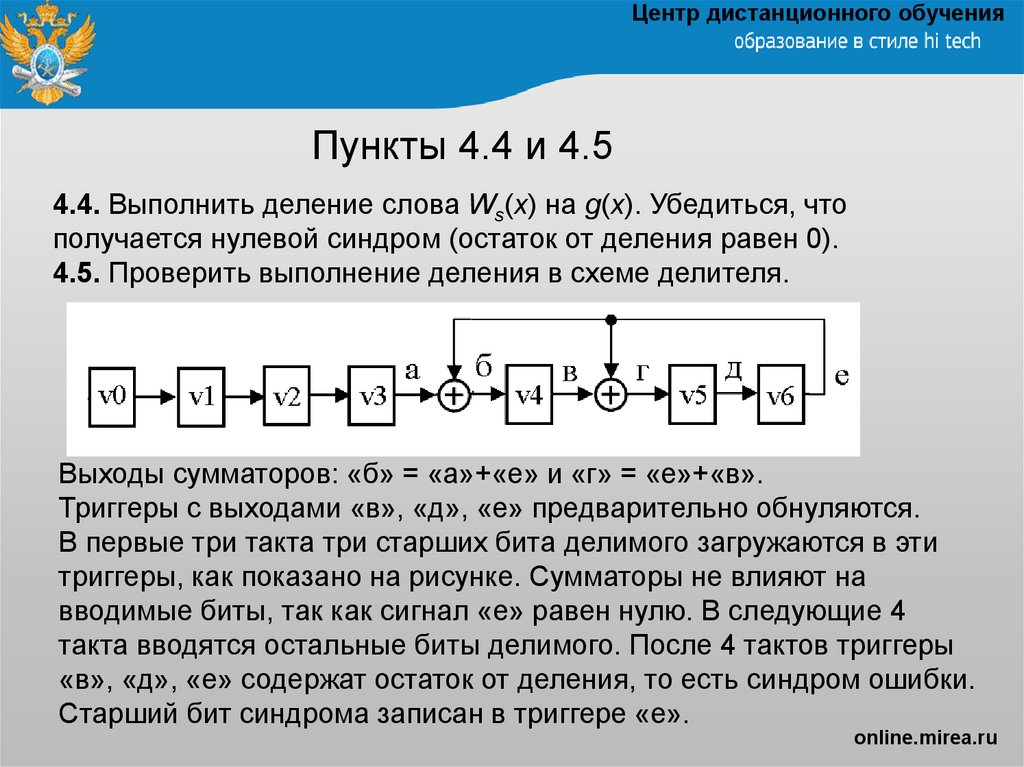
4.4. Выполнить деление слова Ws(x) на g(x). Убедиться, что
получается нулевой синдром (остаток от деления равен 0).
4.5. Проверить выполнение деления в схеме делителя.
Выходы сумматоров: «б» = «а»+«е» и «г» = «е»+«в».
Триггеры с выходами «в», «д», «е» предварительно обнуляются.
В первые три такта три старших бита делимого загружаются в эти
триггеры, как показано на рисунке. Сумматоры не влияют на
вводимые биты, так как сигнал «е» равен нулю. В следующие 4
такта вводятся остальные биты делимого. После 4 тактов триггеры
«в», «д», «е» содержат остаток от деления, то есть синдром ошибки.
Старший бит синдрома записан в триггере «е».
online.mirea.ru
12. Пункт 4.5. Окончание
Центр дистанционного обученияПункт 4.5. Окончание
Выходы триггеров:
«в», «д», «е».
Выходы сумматоров:
«б» = «а»+«е»;
«г» = «е»+«в».
Положения битов входного слова после первых трех тактов
(строка 0 таблицы): v6 в «е»; v5 в «д»; v4 в «в»; v3 в «а».
В следующие 4 такта в триггеры вводятся остальные биты
делимого. После 4 тактов (строка 4) триггеры «в», «д», «е»
содержат остаток от деления, то есть синдром ошибки. Старший
бит синдрома записан в триггере «е».
online.mirea.ru
13. Пункты 4.6 и 4.7
Центр дистанционного обученияПункты 4.6 и 4.7
4.6. Ввести в Ws(x) одиночную ошибку. Выполнить деление.
Получить синдром. Проверить, правильно ли указывает синдром на
сделанную ошибку.
4.7. Проверить выполнение деления в схеме делителя.
Выходы триггеров:
«в», «д», «е».
Выходы сумматоров:
«б» = «а»+«е»;
«г» = «е»+«в».
В строке 0 разряд v6 в «е».
Передается кодовое слово 1111111, полученное из информационного
слова 1111. Принято слово 1110111, содержащее ошибку в третьем
разряде e3(x) = x3. Синдром ошибки 011 или x + 1 правильно
показывает на разряд, в котором ошибка.
online.mirea.ru
14. Пункты 4.8 и 4.9
Центр дистанционного обученияПункты 4.8 и 4.9
4.8. Ввести в Ws(x) другую одиночную ошибку. Выполнить деление.
Получить синдром. Проверить, правильно ли указывает синдром на
сделанную ошибку.
4.9. Ввести в Ws(x) обе одиночные ошибки по п. 4.6 и п. 4.8.
Вычислить синдром. Правильно ли он указывает на ошибку?
В этих пунктах не надо выполнять деление в схеме. Достаточно
выполнить деление в столбик.
online.mirea.ru
15. Пункт 4.10
Центр дистанционного обученияПункт 4.10
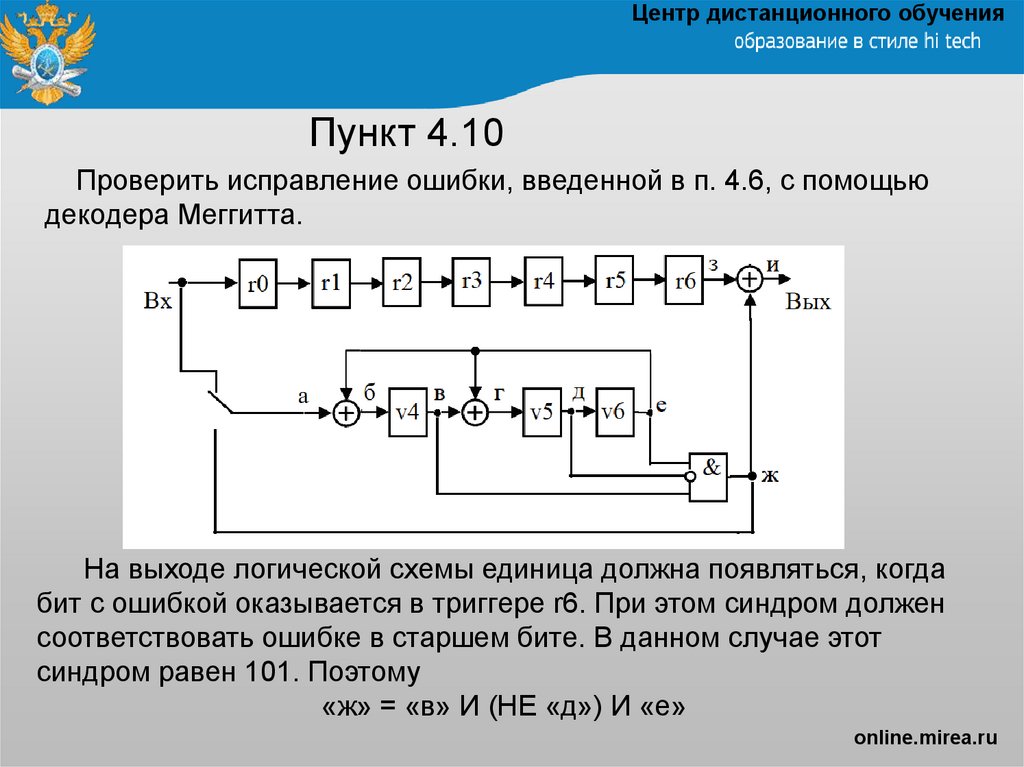
Проверить исправление ошибки, введенной в п. 4.6, с помощью
декодера Меггитта.
На выходе логической схемы единица должна появляться, когда
бит с ошибкой оказывается в триггере r6. При этом синдром должен
соответствовать ошибке в старшем бите. В данном случае этот
синдром равен 101. Поэтому
«ж» = «в» И (НЕ «д») И «е»
online.mirea.ru
16. Пункт 4.10. Продолжение
Центр дистанционного обученияПункт 4.10. Продолжение
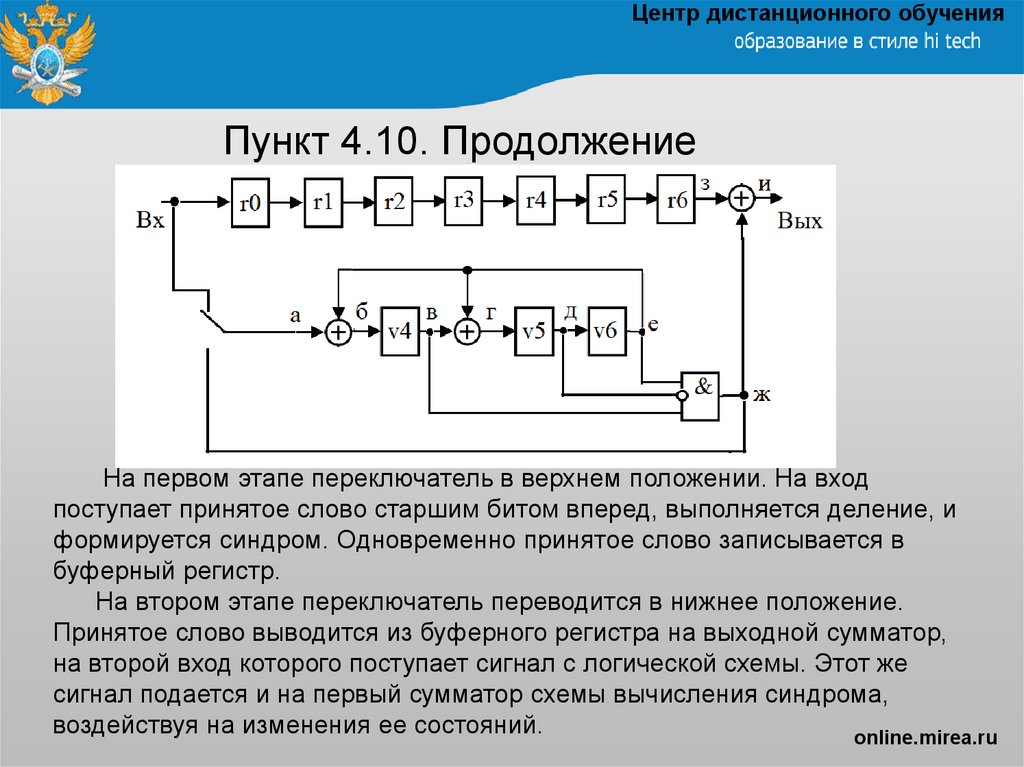
На первом этапе переключатель в верхнем положении. На вход
поступает принятое слово старшим битом вперед, выполняется деление, и
формируется синдром. Одновременно принятое слово записывается в
буферный регистр.
На втором этапе переключатель переводится в нижнее положение.
Принятое слово выводится из буферного регистра на выходной сумматор,
на второй вход которого поступает сигнал с логической схемы. Этот же
сигнал подается и на первый сумматор схемы вычисления синдрома,
воздействуя на изменения ее состояний.
online.mirea.ru
17. Пункт 4.10. Окончание
Центр дистанционного обученияПункт 4.10. Окончание
Выходы триггеров:
«в», «д», «е».
Выходы сумматоров:
«б» = «а»+«е»;
«г» = «е»+«в».
Передано: 1111111.
Принято: 1110111.
Синдром в «е», «д», «в».
«ж»=«в» И (НЕ«д») И «е».
В строке 0 показаны состояния точек схемы после перевода
переключателя в верхнее положение.
В столбце «з» показаны биты принятого слова, поступающие из
буферного регистра.
Когда на выходе буферного регистра появляется бит с ошибкой, в
точках «ж» и «а» оказывается единица. В результате ошибочный бит
исправляется, а триггеры регистра синдрома обнуляются.
online.mirea.ru
18. Пункт 5.1
Центр дистанционного обученияПункт 5.1
5.1. Построить проверочную матрицу систематического кода
Хемминга (7,4), имеющую 3 строки и 7 столбцов. Получить из нее
проверочную матрицу расширенного кода, дополнив сначала
столбцом из 3 нулей слева, а затем строкой из 8 единиц сверху.
online.mirea.ru
19. Пункты 5.2 – 5.6
Центр дистанционного обученияПункты 5.2 – 5.6
5.2. Кодовое слово, полученное в п.4.1, дополнить слева битом
проверки четности, получив кодовое слово расширенного кода
Хемминга.
5.3. Рассчитать синдром, выполнив умножение кодового слова на
транспонированную проверочную матрицу. Убедиться, что синдром
равен 0.
5.4. Ввести одиночную ошибку как в п.4.6. Рассчитать синдром.
Сопоставить его с синдромом по п.4.6.
5.5. Ввести одиночную ошибку как в п.4.8. Рассчитать синдром.
Сопоставить его с синдромом по п.4.8.
5.6. Ввести обе ошибки как в п.4.9. Рассчитать синдром. Отметить в
отчете, какое свойство синдрома при двойной ошибке позволяет ее
обнаружить в режиме исправления.
online.mirea.ru
20. Пункт 6. Код CRC
Центр дистанционного обученияПункт 6. Код CRC
6.1. Построить последовательность из 16 битов. Для этого взять 4
последние цифры номера своего телефона и записать их 4-битовые коды.
6.2. Получить контрольную сумму последовательности с помощью кода
CRC-4, имеющего порождающий полином g(x) = x4 + x + 1. Записать
передаваемую последовательность.
Контрольной суммой называется остаток от деления последовательности
на порождающий полином. Алгоритм вычисления этого остатка описан в
Приложении П4.
6.3. Ввести в последовательность по п.6.1 одну ошибку. Вычислить
контрольную сумму. Сравнить с результатом п.6.2.
6.4. Ввести в последовательность по п.6.1 две ошибки. Вычислить
контрольную сумму. Сравнить с результатом п.6.2.
6.5. Ввести в последовательность по п.6.1 три ошибки. Вычислить
контрольную сумму. Сравнить с результатом п.6.2.
6.6. Ввести в последовательность по п.6.1 четыре ошибки. Вычислить
контрольную сумму. Сравнить с результатом п.6.2.
6.6. Сопоставить результаты с ответом на вопрос по п.2.7.
online.mirea.ru
21. Пример вычисления контрольной суммы
Центр дистанционного обученияПример вычисления контрольной суммы
online.mirea.ru
22. Пояснения к примеру
Центр дистанционного обученияПояснения к примеру
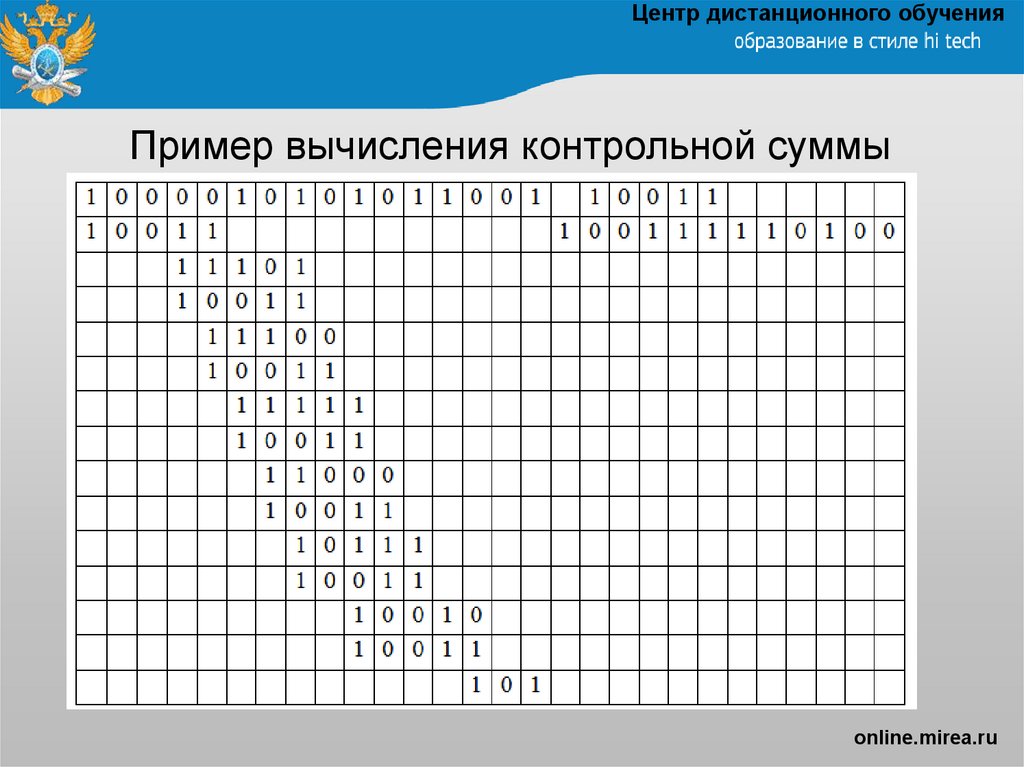
Вычисление остатка от деления кодируемой последовательности
на порождающий многочлен кода CRC может быть выполнено в
столбик, как показано ниже. Единица записывается в частное
всегда, когда старший бит из 5 битов текущего операнда равен «1».
При этом выполняется сложение по модулю 2 этих пяти битов с
делителем. Если же указанный бит равен «0», то в частное
записывается «0».
Остаток от деления должен содержать 4 бита, так как старшая
степень делителя равна 4. Поэтому в данном примере результат
будет равен 0101.
Известны алгоритмы, позволяющие находить остаток от деления
эффективнее, чем данный простой алгоритм. Информацию о них
можно найти в Интернете.
online.mirea.ru
23.
Центр дистанционного обученияСпасибо за внимание!
online.mirea.ru

















 informatics
informatics








