Лекция №5 (5). Электромагнитные поля элементарных источников

1. Тема 2. ИЗЛУЧЕНИЕ ЭМВ В СВОБОДНОЕ ПРОСТРАНСТВО Лекция №5 (5). Электромагнитные поля элементарных источников

1.
2.
3.
4.
Общие характеристики ЭМП элементарных источников.
Поля элементарных электрического и магнитного вибраторов.
Диаграмма направленности.
Сферические волны. Поле электрического и магнитного
вибраторов.
Цилиндрические волны. Структура поля линейного
электрического и магнитного излучателей.
Электродинамика и РРВ.Сем.1. Лекция 5(5).
1

2. 1 Общие характеристики ЭМП элементарных источников

Решение задачи об излучении:
- электрического типа
э
Am (r )
~a
V
~
exp( ik r )
jmэ.ст (r ')
dv
4 r
- магнитного типа
м
Am (r ) ~a
V
~
exp(
i
k
r)
м.ст
jm (r ')
dv
4 r
~
exp( ik r )
G (r , r ')
4 r
- функция Грина.
Функция Грина – истокообразная, т.е. описывающая возбуждение
поля. Математически данное явление соответствует обращению
в нуль знаменателя (случай, когда расстояние между точкой
наблюдения и точкой источника совпадает).
Электродинамика и РРВ.Сем.1. Лекция 5(5).
2

3.

Структура поля излучателя – распределение по зонам.
1. Ближняя зона
r r r '
2. Зона Френеля
r r r'
3. Зона излучения,
зона Фраунгофера
r r r '
В задачах ЭД решение осуществляется по зонам.
Ближняя зона рассматривается при решении задач по
электромагнитной совместимости, эффекты взаимной связи.
Дальняя зона – при решении задач об излучении.
Электродинамика и РРВ.Сем.1. Лекция 5(5).
3

4.

2 Поля элементарных электрического и
магнитного вибраторов. Диаграмма
направленности
Элементарным электрическим излучателем называют элемент
электрического линейного тока, характеризуемый следующими
особенностями:
1) его длина весьма мала по сравнению с длиной волны
создаваемого им поля , а радиус меньше длины a ,
2) в каждый момент времени ток имеет одно и то же значение
I ( z, t ) const .
Элементарный магнитный излучатель – это воображаемый
«проводник» длиной , по которому протекает фиктивный
магнитный ток .
Примеры реализации: диполь Герца (электрический тип), рамка с
током, щель в экране (магнитный тип).
Электродинамика и РРВ.Сем.1. Лекция 5(5).
4

5.

Нахождение структуры поля элементарного
электрического излучателя.
Замечания по геометрии:
1) Об используемой системе координат: Используется
та система координат, в которой одна из координатных
поверхностей совпадает с поверхностью излучателя
(для разделения компонент ЭМП).
2) Ориентация излучателя: образующая излучателя
должна совпадать с осью 0z.
3) Отсчет углов: от оси вибратора.
Электродинамика и РРВ.Сем.1. Лекция 5(5).
5

6.

Нахождение структуры поля элементарного электрического
излучателя
1) Решение задачи в декартовой системе координат.
Распределение стороннего тока
в излучателе:
э
j (r ') zI 0 ( x 0) ( y 0) ( z 0)
Электродинамический потенциал с
учетом свойств дельта-функции
exp( ikr )
A (r ) z
I 0
4 r
э
2) Переход в сферическую систему координат :
exp( ikr )
I 0 cos
4 r
э
exp( ikr )
э
A A sin
I 0 sin
4 r
э
ARэ A cos
Электродинамика и РРВ.Сем.1. Лекция 5(5).
A э 0
6

7.

Нахождение структуры поля элементарного электрического
излучателя
3) Нахождение компонент ЭМП с помощью уравнений связи:
H 0
H R 0,
ER
I 0
I 0
H
(1 ikr) sin exp( ikr)
2
4 r
(1 ikr) cos exp( ikr)
2 a r
I 0
2 2
E
(
1
ikr
k
r ) sin exp( ikr)
3
4 a r
3
E 0
Анализ структуры поля
Ближняя зона. Пренебрегаем вкладом слагаемых, у которых есть
множители r 1 , Получаем три отличные от нуля компоненты
I
H 0 2 sin
4 r
iI 0
ER
cos
3
2 a r
E
Электродинамика и РРВ.Сем.1. Лекция 5(5).
iI 0
sin
3
4 a r
7

8.

Анализ структуры поля
Дальняя зона. Пренебрегаем вкладом слагаемых, у которых
множители имеют порядок, больший чем r 1 . От нуля будут
отличны только две компоненты:
I 0 k 2
exp( ikr)
E
sin
4 a
r
I 0
exp( ikr )
H
sin
4
r
Для поля элементарного магнитного излучателя используем
принцип двойственности. В результате получаем:
I м 0 k 2
exp( ikr)
H
sin
4 a
r
I м 0
exp( ikr )
E
sin
4
r
Структура поля – сферические волны, уходящие от источника
(множитель exp( ikr ) / r ).
В дальней зоне поле квазиплоское (отсутствует R-компонента).
Соотношение между компонентами – величина постоянная:
E
E
- волновое число свободного
W0 120 Ом
H
H
пространства
8
Электродинамика и РРВ.Сем.1. Лекция 5(5).

9.

Структура поля – сферические волны, уходящие от источника
(множитель exp( ikr ) / r ).
В дальней зоне поле квазиплоское (отсутствует R-компонента).
Соотношение между компонентами – величина постоянная:
E
E
W0 120
H
H
Ом
- волновое число свободного
пространства
9
Электродинамика и РРВ.Сем.1. Лекция 5(5).

10.

Диаграмма направленности.
Распределение поля излучения в пространстве при R=const
характеризуется при помощи функции, называемой
характеристикой направленности:
F ( , )
U ( , )
U ( , )
max
Традиционно для излучателей электрического типа используется
характеристика направленности, полученная относительно
распределения электрического поля (U E),
а для излучателей магнитного типа – относительно распределения
магнитного поля ( U H ).
Для элементарных электрического и магнитного излучателей
характеристика направленности имеет вид:
F ( , ) sin
График функции направленности называется диаграммой
направленности.
10
Электродинамика и РРВ.Сем.1. Лекция 5(5).

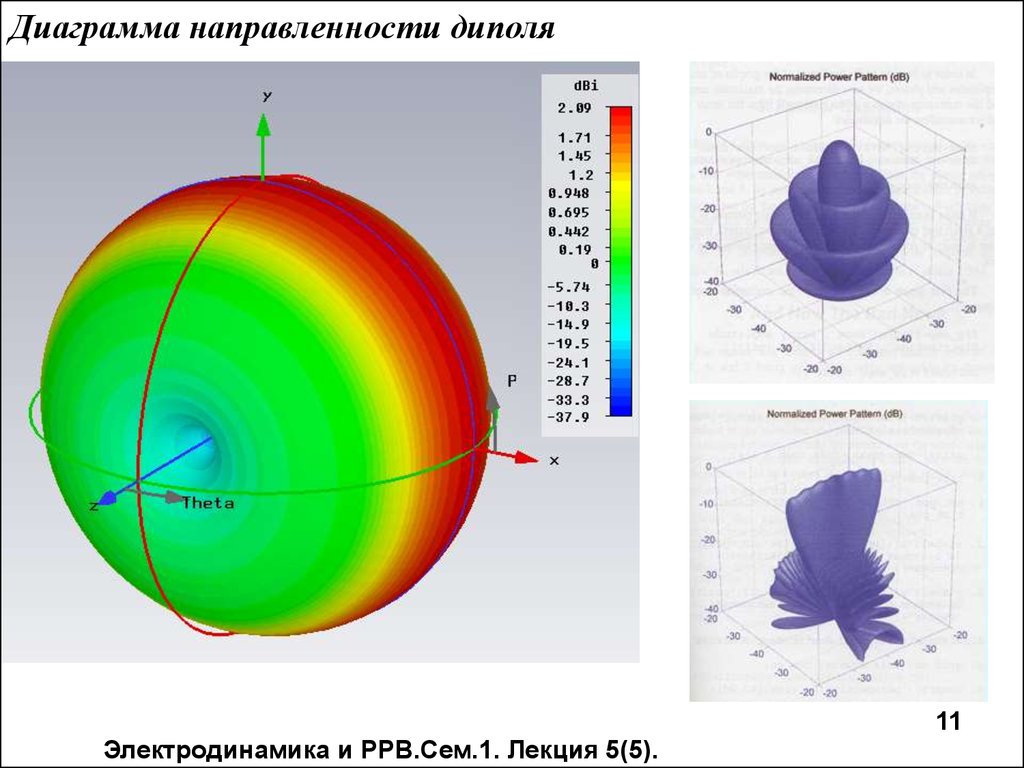
11.

Диаграмма направленности диполя
11
Электродинамика и РРВ.Сем.1. Лекция 5(5).

12.

Поле диполя
12
Электродинамика и РРВ.Сем.1. Лекция 5(5).

13.

Поле диполя
13
Электродинамика и РРВ.Сем.1. Лекция 5(5).

14.

3 Сферические волны. Поле электрического и
магнитного вибраторов
Геометрия задачи
Распределение тока
j
э ст
I э ( z ) exp[ i ( z )], z L,
( z) iz
z L
0
Выражение для потенциала
э
A ix
1
exp( ikr)
э
I
(
z
'
)
exp[
i
(
z
'
)]
dz '
4 L
r
r x 2 y 2 ( z z' ) 2
14
Электродинамика и РРВ.Сем.1. Лекция 5(5).

15.

Компоненты ЭМП:
H R 0,
H 0
H
ER
exp( ikr )W
(sin H )
kr sin
E
exp( ikr )W
(r H )
kr
r
exp( ikr)
э
э
r
sin
A
cos
A
z
z
r
r
E 0
При kr (в дальней зоне) поле имеет две поперечные
относительно направления распространения синфазные
составляющие.
Фронт волны (поверхность фаз) представляет собой сферу
(сомножитель exp( ikr ) ) . Однако поле зависит еще и от угловой
координаты . Такая волны называется неоднородной
сферической волной.
15
Электродинамика и РРВ.Сем.1. Лекция 5(5).

16.

4 Цилиндрические волны. Структура поля
линейного электрического и магнитного
излучателей
Источник является протяженным – линейным излучателем
(например, бесконечно длинный провод с радиусом,
намного меньше длины волны)).
Распределение стороннего тока:
ст
j (r ') i z I 0э (r a) ( 0)
Векторный потенциал в цилиндрической
системе координат:
I 0э ( 2)
A (r ) i z H 0 (kr )
4i
э
где
H 0( 2) ( )
- функция Ганкеля 2-го рода
нулевого порядка.
16
Электродинамика и РРВ.Сем.1. Лекция 5(5).

17.

I 0э
( 2)
H
k
H
1 (kr )
Компоненты ЭМП:
4i
k
exp[ ikr i / 4]
В дальней зоне: H
8 r
I 0э
E z kW0 H 0( 2) (kr )
4i
E z H W0
ЭМП распространяется в направлениях, перпендикулярных нити.
Имеет две поперечные относительно направления
распространения синфазные составляющие (Ez и H ,) - T-волна.
Фаза меняется по r при kr по закону бегущей волны.
Фронт волны представляет собой бесконечный цилиндр с осью,
совпадающей с нитью тока. Амплитуды составляющих векторов
поля убывает с ростом r по закону, определяемому функцией 1
r
Составляющие векторов поля однородны по азимутальному углу
и по координате z. Волну этого типа называют однородной
цилиндрической волной.
Для магнитного излучателя:
м
I 0м ( 2)
E
H1 (kr )
4i
I 0 k ( 2)
Hz
H 0 (kr )
4W
Электродинамика и РРВ.Сем.1. Лекция 5(5).
17