Кванторы существования и общности

1.

Кванторы
существования и общности
Выполнил: Дмитриева С.А. преподаватель ОГБПОУ
«Северский промышленный коллдж»

2.

Для количественных характеристик обычно
используют понятия «все», «некоторые»,
«существуют» и др., которые называют
кванторами (от лат. quantum - сколько).
Такие кванторы, как (любой, для всех) и
(существует) используются в математике. Как
действуют
данные
кванторы
для
высказывательных форм – мы рассмотрим в
данной презентации.

3.

Как нам уже известно

4.

5.

Запись х² - 5х = 0 х(х – 5) = 0
Является
не
формулой,
а
истинным
высказыванием
о
равносильности двух формул,
представленных
в
виде
уравнений.

6.

В то же время справедлива запись
х (х² - 5х = 0) (х(х – 5) = 0),
выражающая
истинное
высказывание, которое включает
операцию
эквиваленции
в
качестве составляющей.

7.

Поэтому логическое следование
можно
определить
через
импликацию, а равносильность
через эквиваленцию.

8.

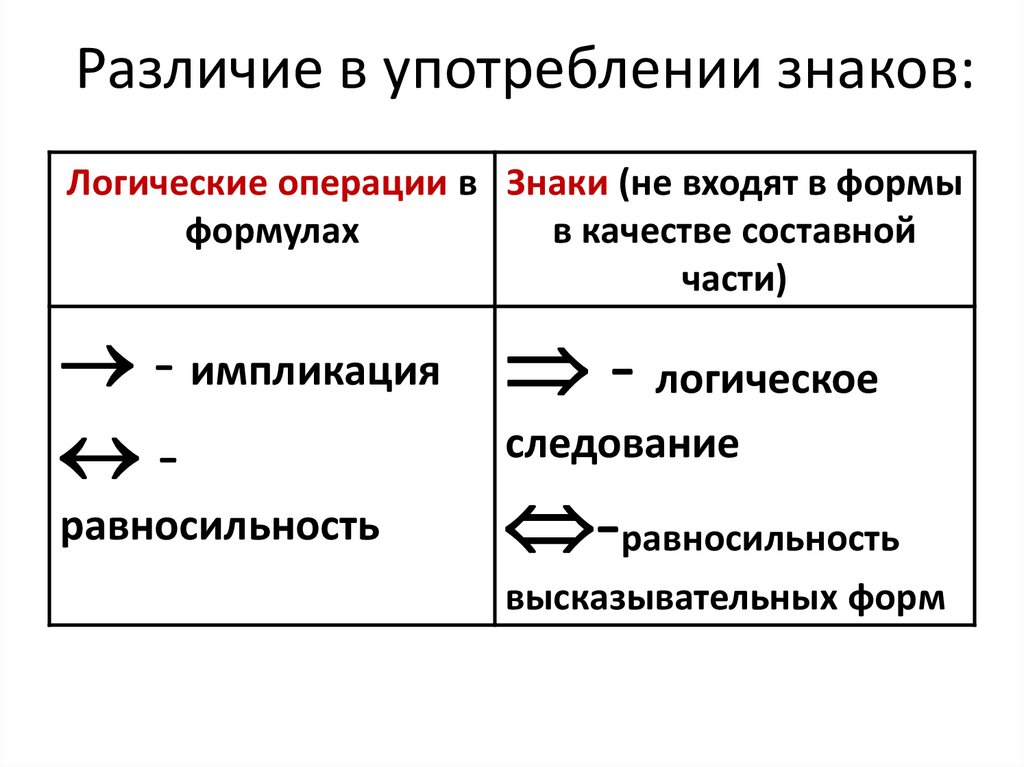
Различие в употреблении знаков:
Логические операции в Знаки (не входят в формы
формулах
в качестве составной
части)
- импликация - логическое
следование
равносильность
-равносильность
высказывательных форм

9.

10.

Например
В выражении переменная х связывает
свойство
предиката
и
квантор
общности.
хР(х)
Грубо говоря, от этой переменной, её
конкретного вида и имени, ничего не
зависит, т.е. хР(х) и уР(у)
суть одно и то же.

11.

12.

Часть формулы, на которую распространяется
действие квантора, называется областью
действия этого квантора.
Вхождение переменной в формулу может
быть
связанным,
если
переменная
расположена либо непосредственно после
знака квантора, либо в области действий
квантора, после которого стоит переменная.
Все прочие вхождения – свободные.

13.

например, в формуле
А (х1, х2) х1 В(х1)
первое включение переменной
х1
свободное,
связанное.
а
второе
–

14.

Переменная, не являющаяся связанной,
называется свободной, если после
подстановки
вместо
нее
имени
некоторых
конкретных
объектов
предикат превращается в осмысленное
предложение.
Кванторы общности и существования
являются дополнениями и аналогами
соответственно логических операций
конъюнкции и дизъюнкции.

15.

16.

17.

Например
Запишем с помощью формул логики
предикатов
следующее
утверждение: «Для лечения любого
известного компьютерного вируса
имеются программы. Существуют
новые
(неизвестные)
компьютерные
вирусы,
для
лечения которых программы еще
не разработаны».

18.

Введем обозначения
элементарных формул:
А(х) – известен компьютерный вирус х.
В(х) – для лечения вируса х существует
программа.

19.

Тогда с помощью логических связок и
кванторов получим формулы:
В(х) – против вируса х нет программы;
х(А(х)) – любой вирус известен;
х(А(х))
–
существуют
новые
(неизвестные) вирусы;
х(А(х)→В(х)) – если вирус давно
известен, то имеется программа для его
лечения;

20.

х(А(х) В(х))
существуют
(появились) новые вирусы, для
лечения которых программы еще не
разработаны.
Тогда формализованное исходное
утверждение примет вид:
–
( х(А(х)→В(х))) ( х(А(х) В(х)))