Similar presentations:
Производная функции
1.
МатематикаПреподаватели:
Кормилицына Елена Анатольевна,
Федотова Екатерина Алексеевна
2.
Тема 2.Производная
функции
3.
План лекцииВведение.
1. Приращение аргумента и
функции.
2. Непрерывность функции.
3. Понятие производной функции
4. Геометрический смысл
производной.
5. Физический смысл производной.
4.
ВведениеИзучая поведение функции
f (x ) в окрестности некоторой
точки
, важно знать, как
0
меняется значение функции при
изменении значения аргумента.
Для этого введём понятие
приращения аргумента и
приращения функции.
x
5.
1. Приращение аргумента ифункции.
Опр. Окрестностью точки
0
называется интервал
x
( x0 r; x0 r ),
где число r будем называть
радиусом окрестности.
6.
Рассмотрим небольшой пример.Пусть дан интервал (5,9 ; 6,1) он
будет являться окрестностью
точки 6, следовательно радиус
r = 0,1.
7.
Пусть дана функция f (x ).Рассмотрим два значения её
аргумента : исходное x0 и
новое .
Так же заметим, что точка
лежит в окрестности точки x0 .
x
x
8.
Опр. Разность x x0
называется приращением
аргумента(при переходе от
точки x0 к точке x ) и
обозначается x (дельта икс),
то есть
x x x0 .
9.
Аналогично, разностьf ( x) f ( x0 )
называется приращением
функции и обозначается f
(дельта эф), то есть
f f ( x) f ( x0 ).
10.
Выразим приращение x0 .функции через точку
Итак, если x x x0
следовательно x x0 x,
отсюда
f f ( x0 x) f ( x0 ).
11.
2. Непрерывность функцииОпр. Функция f (x )
называется непрерывной в
точке x0 ,если выполняется
условие
lim f ( x) f ( x0 )
x x0
12.
При этом предполагалось, чтофункция f (x ) определена в
точке x0 и в некоторой её
окрестности.
Дадим определение
непрерывности функции,
пользуясь понятиями
приращения функции и
аргумента.
13.
Действительно, определениевыше равносильно равенству
lim f ( x) f ( x0 ) 0
x x0
Полагая f f ( x) f ( x0 ),
x x x0 и замечая, что при
x x0 x 0.
14.
Т.о., функция непрерывна,если выполняется условие
lim f 0,
x 0
то есть бесконечно малому
приращению аргумента
соответствует бесконечно
малое приращение функции.
15.
3. Понятие производнойфункции
Опр. Пусть функция f (x )
определена в точке x0 и в её
окрестности. Дадим аргументу
приращение x в точке
0
такое, чтобы остаться в
окрестности точки
,
0
x
x
16.
то есть величина x x0
так же лежит в окрестности
точки 0 Если существует
предел отношения
приращения функции f
к приращению аргумента
при условии x 0,
x.
x,
17.
то он называется производнойфункции f (x ) в точке
0
и обозначается
0
Таким образом по
определению имеем
f ( x0 x) f ( x0 )
f
lim
lim
f ( x0 )
x 0 x
x 0
x
x
f ( x ).
18.
В этом случае функциюназывают f (x )
дифференцируемой(гладкой) в
точке x0 ,а сам процесс
нахождения производной
называют
дифференцированием.
19.
4. Геометрический смыслпроизводной
Опр. Прямую AB,
проведенную через две точки
графика функции f (x )
называют секущей.
20.
Опр. Касательной к графикуфункции в точке A
называется предельное
положение секущей AB, когда
точка B перемещаясь по
кривой, неограниченно
приближается к точке A.
21.
Формулировка. Если к графикуфункции f (x ) в точке
0
провести касательную, то
f ( x0 ) выражает угловой
коэффициент – k(тангенс угла
наклона касательной к графику
функции). То есть
k tg f ( x0 ).
x
22.
5. Физический смыслпроизводной
Формулировка. Предел средней
скорости при t 0
будет выражать мгновенную
скорость v (t ) , а мгновенная
скорость есть производная
пути по времени. То есть
23.
v(t ) lim vср s (t0 )t 0
24.
СПАСИБО ЗАВНИМАНИЕ!






















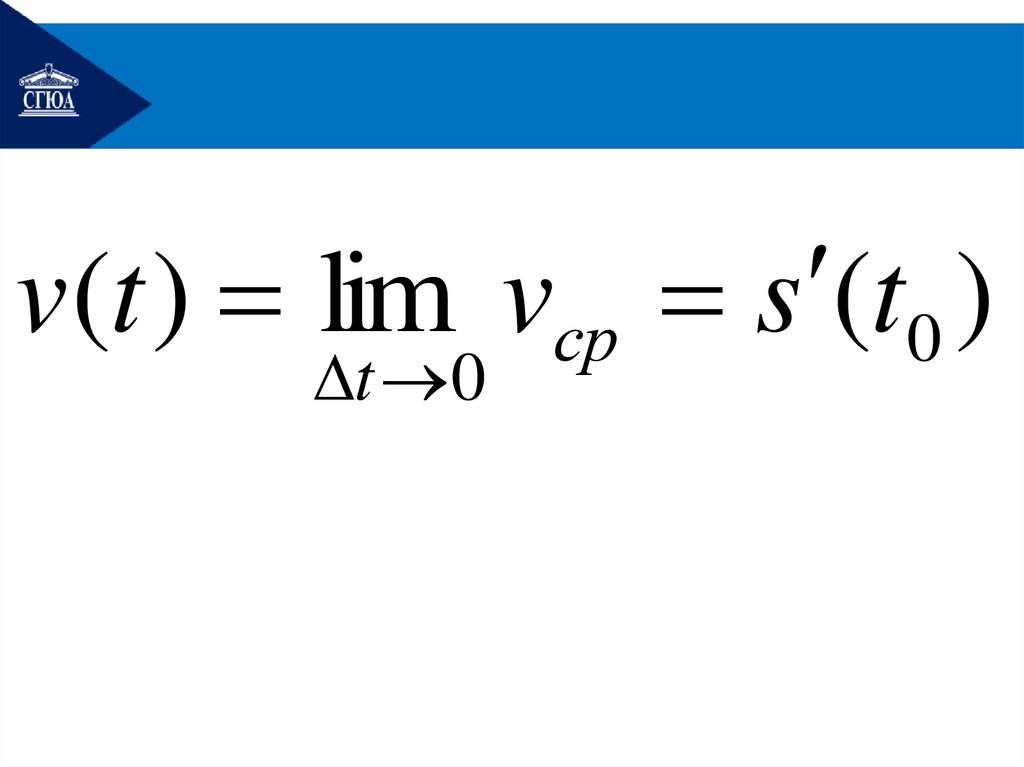

 mathematics
mathematics








