Сила трения

1. Сила трения

Занятие №4

2.

Очень часто при решении статических задач бывает
необходимо учесть силу трения. Для описания силы
трения пользуются законами Кулона:
1. Вектор силы трения лежит в общей касательной
плоскости к поверхностям трущихся тел, тормозя
движение одного тела по поверхности другого, и
имеет величину, пропорциональную нормальной
реакции N, действующей между телами:
Т = kN
Коэффициент
пропорциональности
k
называется
коэффициентом трения.
2. Коэффициент трения не зависит от размеров
соприкасающихся тел.
3. Коэффициент трения существенно зависит от
материала трущихся тел и состояния поверхностей
соприкосновения.

3.

При отсутствии относительного движения тел
величина k не определена, и с ростом
сдвигающей силы k тоже будет возрастать до
некоторой предельной величины, называемой
коэффициентом статического трения
(трения покоя). При дальнейшем увеличении
сдвигающей силы тела сдвигаются друг
относительно друга и коэффициент трения
падает до его значения при движении –
коэффициента динамического трения. В
теоретической механике считается, что он не
зависит от скорости относительного движения.

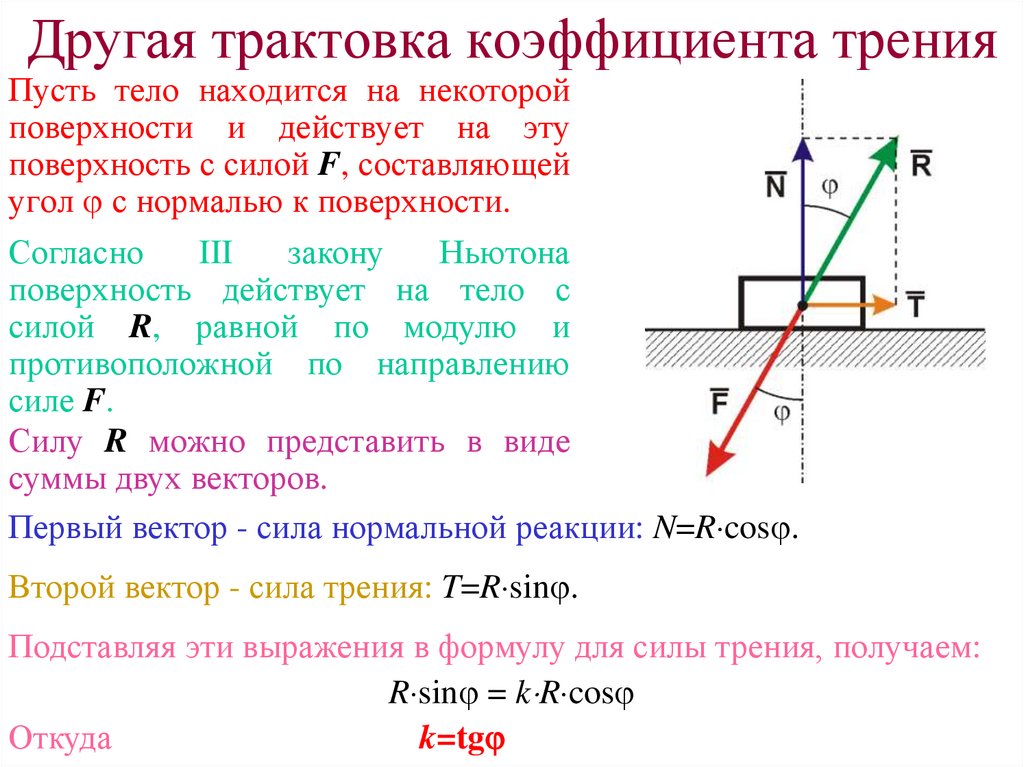
4. Другая трактовка коэффициента трения

Пусть тело находится на некоторой
поверхности и действует на эту
поверхность с силой F, составляющей
угол с нормалью к поверхности.
Согласно
III
закону
Ньютона
поверхность действует на тело с
силой R, равной по модулю и
противоположной по направлению
силе F.
Силу R можно представить в виде
суммы двух векторов.
Первый вектор - сила нормальной реакции: N=R cos .
Второй вектор - сила трения: T=R sin .
Подставляя эти выражения в формулу для силы трения, получаем:
R sin = k R cos
Откуда
k=tg

5.

• Предельное значение угла называется
углом трения. Тело остается в покое, когда угол
между нормалью к поверхности и направлением
действующей силы не превосходит угла . Если
этот угол больше – тело начинает скользить по
поверхности.
• Для решения задач, в которые входят силы
трения, недостаточно только уравнений статики:
их надо дополнять выражениями для силы
трения. Поэтому такие задачи являются
статически неопределимыми.

6. Примеры решения задач

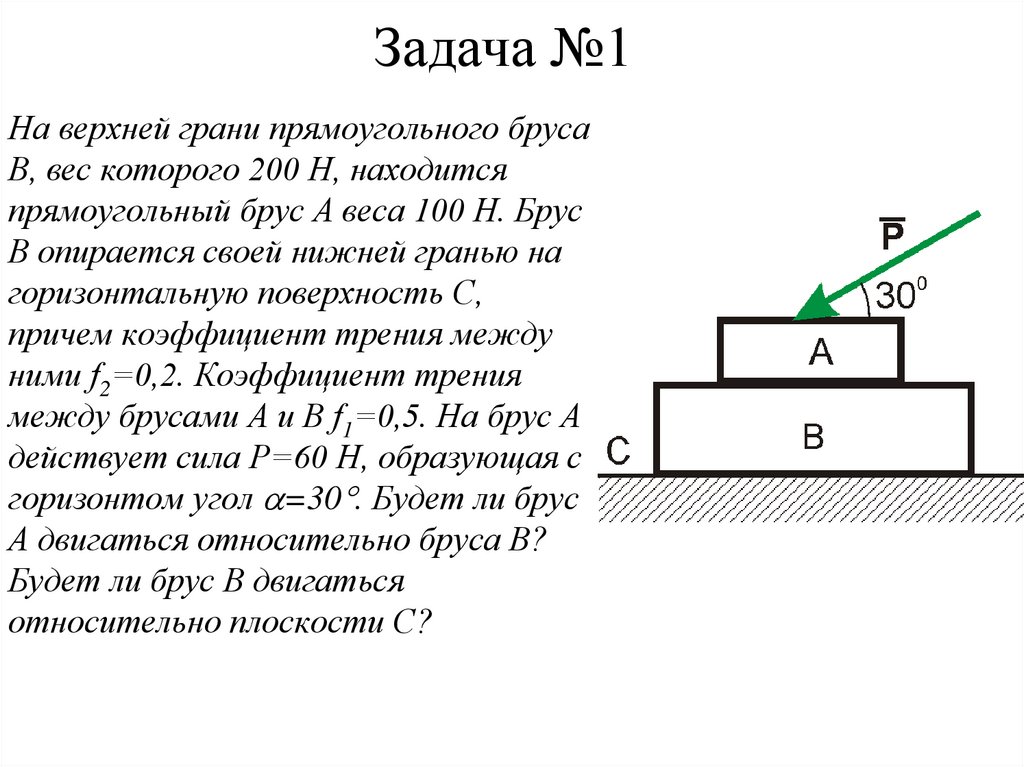
7. Задача №1

На верхней грани прямоугольного бруса
В, вес которого 200 Н, находится
прямоугольный брус А веса 100 Н. Брус
В опирается своей нижней гранью на
горизонтальную поверхность С,
причем коэффициент трения между
ними f2=0,2. Коэффициент трения
между брусами А и В f1=0,5. На брус А
действует сила Р=60 Н, образующая с
горизонтом угол =30 . Будет ли брус
А двигаться относительно бруса В?
Будет ли брус В двигаться
относительно плоскости С?

8.

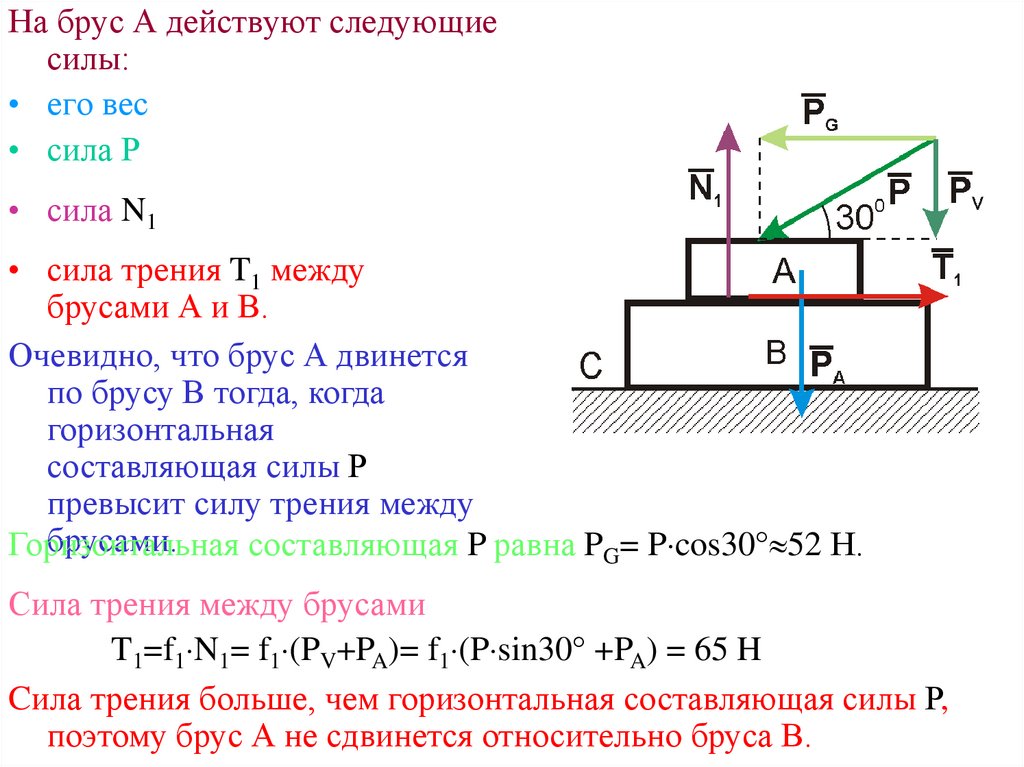
На брус А действуют следующие
силы:
• его вес
• сила Р
• сила N1
• сила трения T1 между
брусами А и В.
Очевидно, что брус А двинется
по брусу В тогда, когда
горизонтальная
составляющая силы Р
превысит силу трения между
брусами.
Горизонтальная
составляющая P равна PG= P cos30 52 Н.
Сила трения между брусами
T1=f1 N1= f1 (PV+PA)= f1 (P sin30 +PA) = 65 H
Cила трения больше, чем горизонтальная составляющая силы Р,
поэтому брус А не сдвинется относительно бруса В.

9.

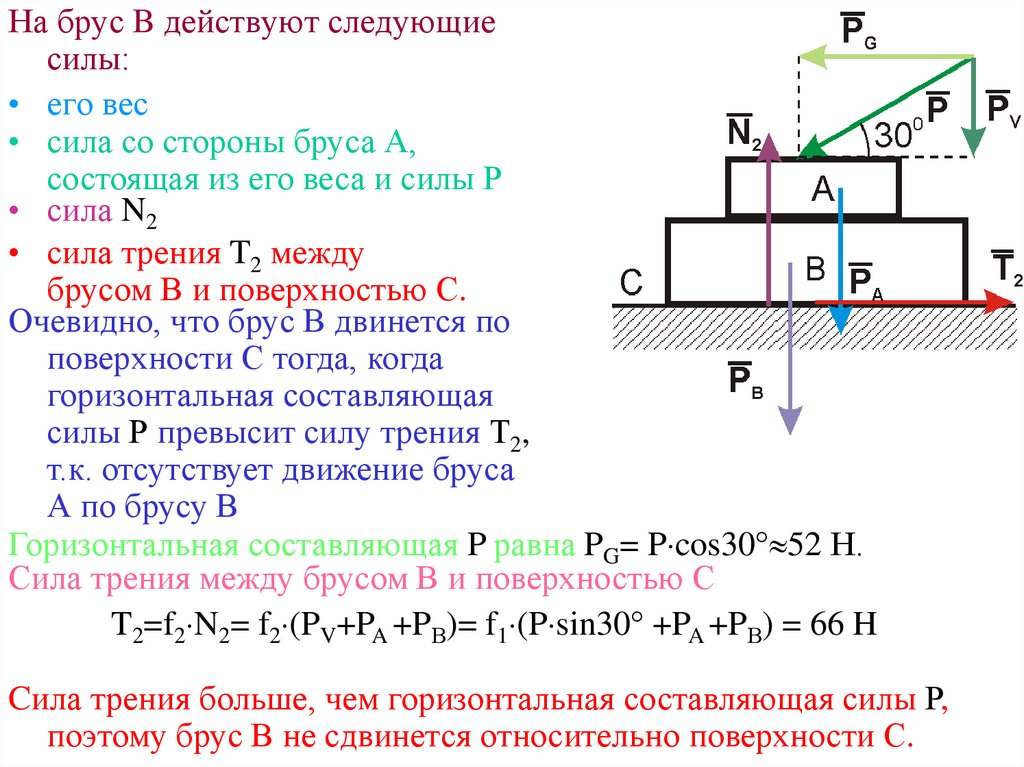
На брус B действуют следующие
силы:
• его вес
• сила со стороны бруса А,
состоящая из его веса и силы Р
• сила N2
• сила трения T2 между
брусом В и поверхностью С.
Очевидно, что брус В двинется по
поверхности С тогда, когда
горизонтальная составляющая
силы Р превысит силу трения Т2,
т.к. отсутствует движение бруса
А по брусу В
Горизонтальная составляющая P равна PG= P cos30 52 Н.
Сила трения между брусом В и поверхностью С
T2=f2 N2= f2 (PV+PA +PВ)= f1 (P sin30 +PA +PВ) = 66 H
Cила трения больше, чем горизонтальная составляющая силы Р,
поэтому брус В не сдвинется относительно поверхности С.

10. Задача №2

Листы бумаги, сложенные, как показано на рисунке, склеиваются
свободными концами через лист, так что получаются две
самостоятельные кипы А и В. Вес каждого листа Q=0,06 Н, число
всех листов 200, коэффициент трения бумаги о бумагу, а также о
стол, на котором бумага лежит, равен 0,2. Предполагая, что одна
из кип удерживается неподвижно, определить наименьшее
горизонтальное усилие Р, необходимое для того, чтобы вытащить
вторую кипу.

11.

Решение
• Сначала рассмотрим случай, когда удерживается кипа В, а кипу А вытаскивают.
Очевидно, что прикладываемая сила FA должна быть не меньше, чем сила трения,
действующая на все листы кипы А.
• Рассмотрим верхний лист кипы А. На каждую его поверхность действует своя сила
трения, равная произведению коэффициента трения на силу нормальной реакции этой
поверхности. Реакция верхней поверхности равна Q (вес листа кипы В, находящегося
над ним), реакция нижней поверхности – 2Q (вес верхних листов обоих кип). Таким
образом, сила трения, действующая на верхний лист кипы А, равна
• P1=f Q + 2f Q
• Рассматривая аналогично второй лист кипы А видим, что сила реакции его верхней
поверхности равна 3Q (над ним – три листа обоих кип), а нижней поверхности – 4Q.
Таким образом,
• P2=3f Q + 4f Q
• Точно также рассматривается третий лист и все остальные. Всего листов. входящих в
кипу – 100 (половина общего их количества), для последнего листа
• P100=199f Q + 200f Q
Общая сила трения, удерживающая кипу А внутри кипы В, равна
FA P1 P2 P3 ... P99 P100 f Q 2 f Q 3 f Q 4 f Q ... 199 f Q 200 f Q
f Q 1 2 3 4 ... 199 200

12.

Выражение в скобках – сумма арифметической прогрессии. Применяя формулу для ее
определения
a1 an
Sn
n
2
получаем:
1 200
FA f Q
200 f Q 20100
2
После подстановки f и Q получаем окончательно
FА=241,2 Н.
Случай, когда кипа В вытаскивается из кипы А, рассматривается аналогично. Применяя
ту же формулу, получаем
FВ= f Q 19900=238,8 Н.

13. Задача №3

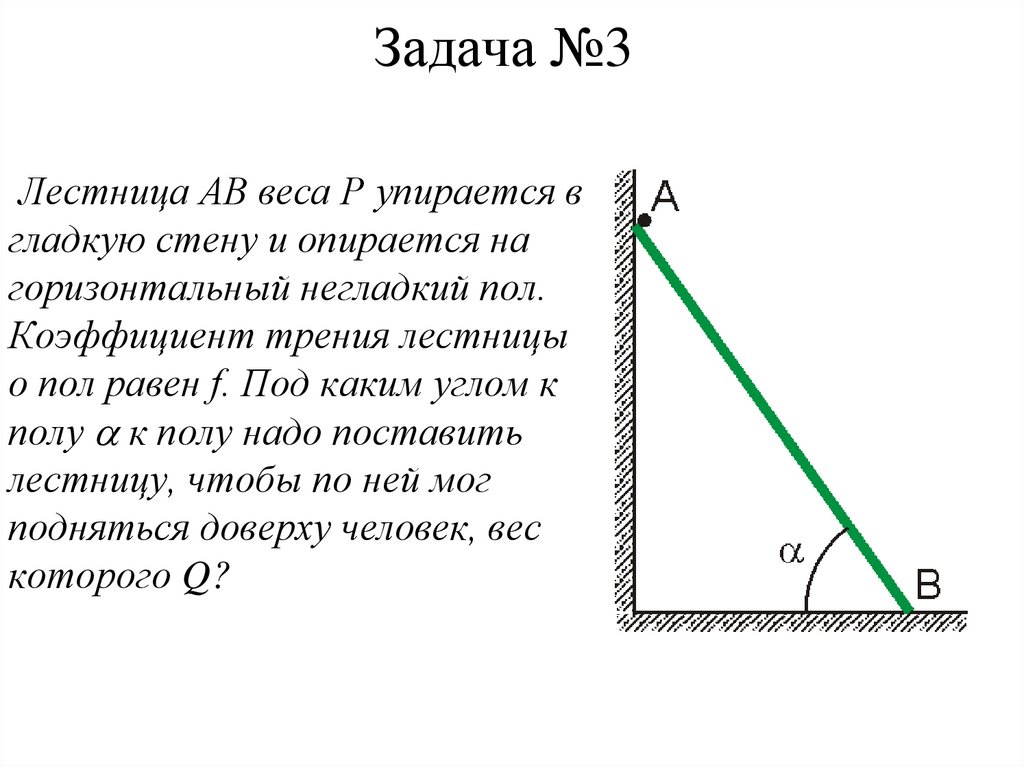
Лестница АВ веса Р упирается в
гладкую стену и опирается на
горизонтальный негладкий пол.
Коэффициент трения лестницы
о пол равен f. Под каким углом к
полу к полу надо поставить
лестницу, чтобы по ней мог
подняться доверху человек, вес
которого Q?

14.

Согласно условия задачи, на лестницу АВ действуют следующие
силы:
• вес лестницы Р,
• вес человека наверху Q,
• нормальная реакция стены в
точке А NA,
• нормальная реакция пола в
точке В NВ
• сила трения между полом и
лестницей F
Согласно общему порядку решения задач статики с произвольной
системой сил, необходимо ввести систему координат и составить
уравнения равновесия.
Уравнения равновесия выглядят так (l – длина лестницы):
Ox:
NA - F = 0;
Oy:
-Q - P + NB = 0;
momB: Q l cos - NA l sin + P (l/2) cos = 0

15.

Так как уравнений статики – три, а неизвестных – четыре (две
нормальные реакции, сила трения и угол наклона лестницы), то
для того, чтобы решить задачу, необходимо дополнить систему
уравнений статики соотношением для силы трения: F=f NB.
После подстановки и элементарных преобразований получается
следующая система для трех неизвестных:
N A f NB 0
NB P Q 0
(2Q P) cos 2 N sin 0
A
Из первых двух уравнений находятся NA и NB; после их
подстановки в последнее уравнение получается следующая
формула для угла наклона :
2Q P
tg
2 f (Q P)
Если угол наклона будет меньше угла , то момент сил тяжестиQ и
P окажется больше момента силы NA относительно точки В, и
лестница соскользнет вниз. Если же угол будет больше – момент
силы тяжести будет меньше, и лестница останется в покое.

16. Задача №4

Однородный стержень своими
концами А и В может скользить
своими концами по негладкой
окружности радиуса а.
Расстояние ОС стержня от
центра О окружности,
расположенной в вертикальной
плоскости, равно b.
Коэффициент трения между
стержнем и окружностью равен
f. Определить для положений
равновесия стержня угол ,
составляемый прямой ОС с
вертикальным диаметром
окружности

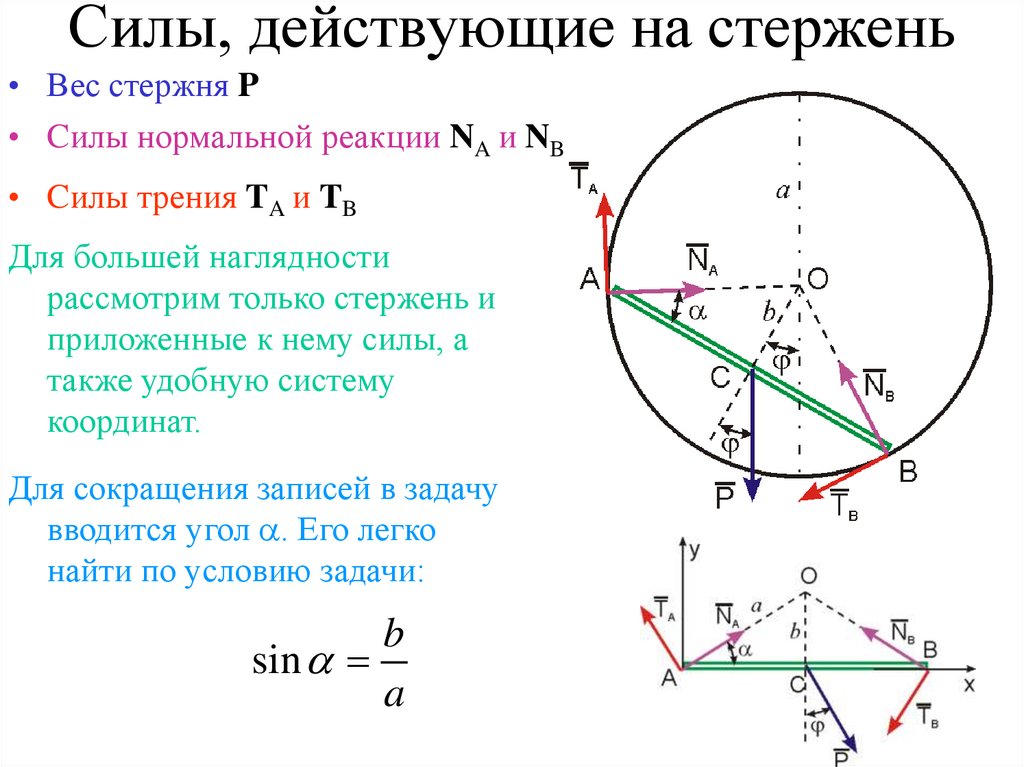
17. Силы, действующие на стержень

• Вес стержня P
• Cилы нормальной реакции NA и NB
• Cилы трения TA и TB
Для большей наглядности
рассмотрим только стержень и
приложенные к нему силы, а
также удобную систему
координат.
Для сокращения записей в задачу
вводится угол . Его легко
найти по условию задачи:
b
sin
a

18.

Уравнения статики составляются
обычным образом. Для того,
чтобы уравнение моментов
оказалось проще, целесообразно
моменты вычислять относительно
центра окружности О.
Ox : N A cos TA sin P sin N B cos TB sin 0
Oy : N A sin TA cos P cos N B sin TB cos 0
momO : Pb sin a(TA TB ) 0
К этим уравнениям нужно добавить соотношения для сил трения:
ТА = f NA, ТB = f NB

19.

После подстановки этих выражений в систему и элементарных
преобразований, система уравнений статики станет такой:
cos ( N A N B ) f sin ( N A N B ) P sin
f cos ( N A N B ) sin ( N A N B ) P cos
Pb sin af ( N N )
A
B
Из первых двух уравнений легко определить сумму (NA+NB):
P(cos f sin )
N A NB
sin (1 f 2 )
Если подставить это выражение в уравнение для моментов и
сократить Р, то получится уравнение для определения угла :
cos f sin
b sin af
sin (1 f 2 )
После деления этого уравнения на sin и замены sin по формуле
получается окончательное выражение для искомого угла:
b (1 f )
ctg f
2
a f
2
2