Тема 8. СИСТЕМЫ СЧИСЛЕНИЯ

1.

ИНФОРМАТИКА
МОДУЛЬ 2 Представление информации в персональных компьютерах
Лекция на тему:
СИСТЕМЫ СЧИСЛЕНИЯ
Лектор:
старший преподаватель
кафедры электроэнергетики и автоматики
Анисимова З.Г.

2.

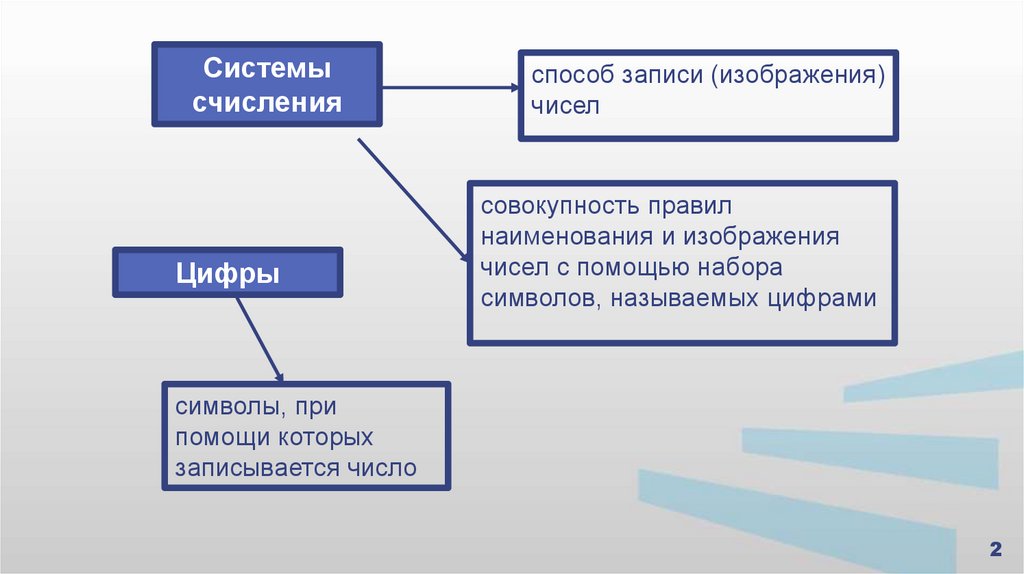
Системы
счисления
Цифры
способ записи (изображения)
чисел
совокупность правил
наименования и изображения
чисел с помощью набора
символов, называемых цифрами
символы, при
помощи которых
записывается число
2

3.

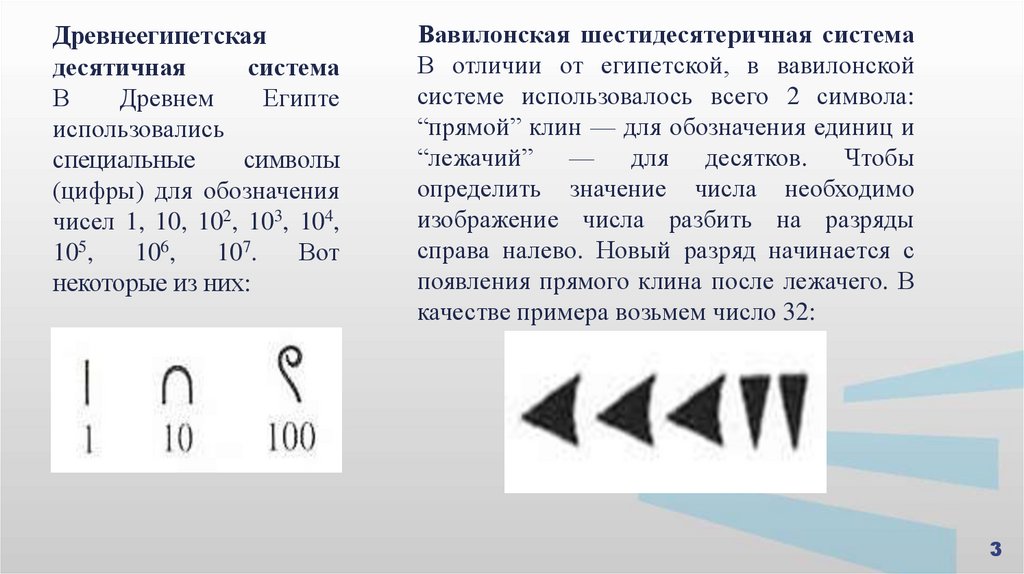
Древнеегипетская
десятичная
система
В
Древнем
Египте
использовались
специальные
символы
(цифры) для обозначения
чисел 1, 10, 102, 103, 104,
105,
106,
107.
Вот
некоторые из них:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской
системе использовалось всего 2 символа:
“прямой” клин — для обозначения единиц и
“лежачий” — для десятков. Чтобы
определить значение числа необходимо
изображение числа разбить на разряды
справа налево. Новый разряд начинается с
появления прямого клина после лежачего. В
качестве примера возьмем число 32:
3

4.

Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел
1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C,
D и M соответственно. Число в римской системе счисления — это набор стоящих
подряд цифр
Помимо цифирных, существуют и буквенные (алфавитные) системы счисления,
такие как: Славянская, Греческая (ионийская).
Шестидесятеричная вавилонская система — первая система счисления, частично
основанная на позиционном принципе. Данная система счисления используется и
сегодня, например, при определении времени — час состоит из 60 минут, а минута из
60 секунд. В Индии система приняла форму позиционной десятичной нумерации с
применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её
переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось
название “арабская”.
4

5.

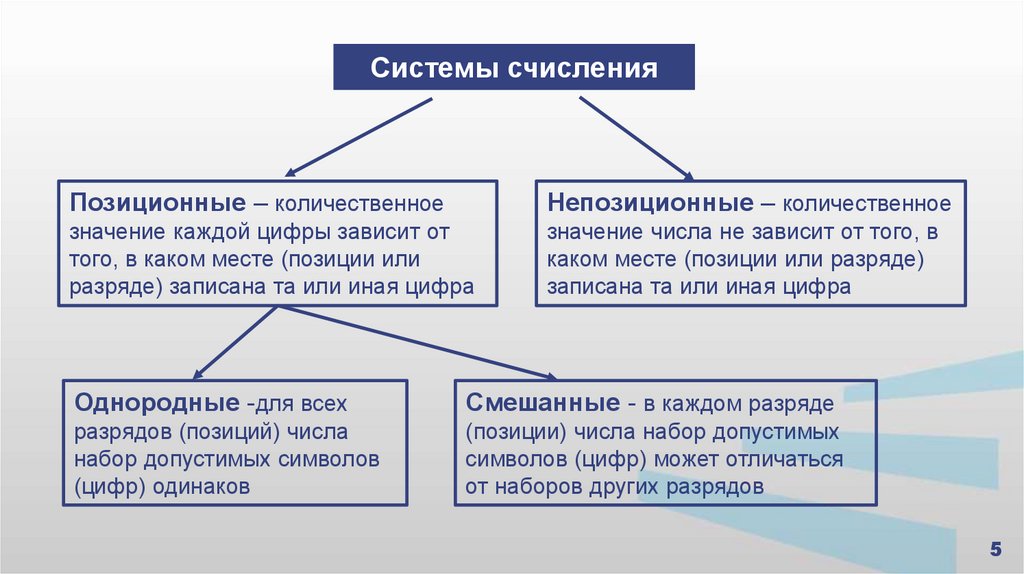
Системы счисления
Позиционные – количественное
Непозиционные – количественное
значение каждой цифры зависит от
того, в каком месте (позиции или
разряде) записана та или иная цифра
значение числа не зависит от того, в
каком месте (позиции или разряде)
записана та или иная цифра
Однородные -для всех
Смешанные - в каждом разряде
разрядов (позиций) числа
набор допустимых символов
(цифр) одинаков
(позиции) числа набор допустимых
символов (цифр) может отличаться
от наборов других разрядов
5

6.

Разряд - это позиция цифры в числе. Разрядность числа количество цифр, из которых состоит число (например, 264 трехразрядное число, 00010101 - восьмиразрядное число).
Разряды нумеруются справа на лево (например, в числе 598
восьмерка занимает первый разряд, а пятерка - третий)
Цель создания системы счисления - выработка наиболее
удобного способа записи количественной информации
6

7.

Основание позиционной системы счисления – это
количество различных знаков или символов, используемых
для изображения цифр в данной системе
Алфавитом системы счисления называется совокупность различных
цифр, используемых в позиционной системе счисления для записи чисел.
Например:
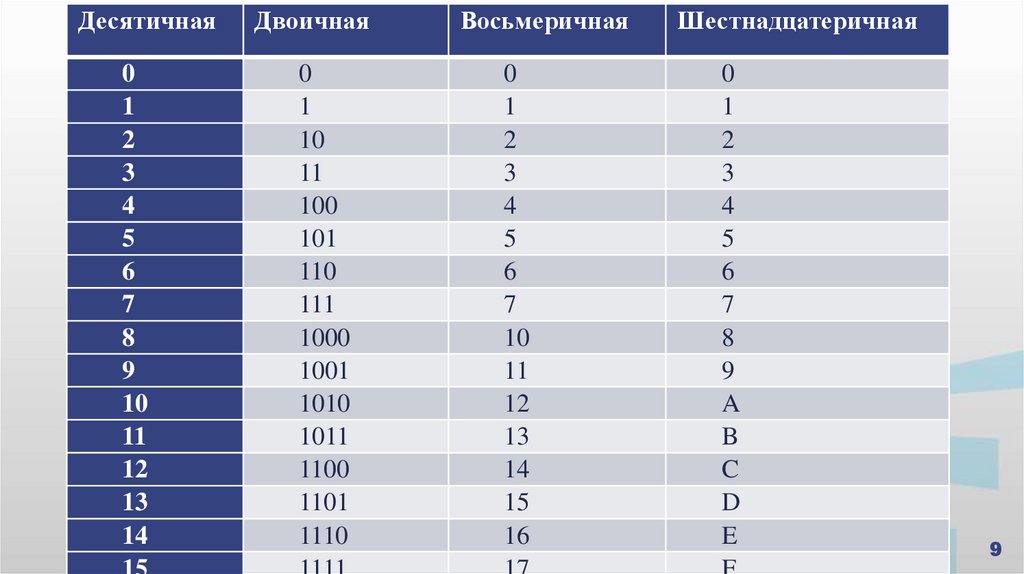
Десятичная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Двоичная система: {0, 1}
Восьмеричная система: {0, 1, 2, 3, 4, 5, 6, 7}
Шестнадцатеричная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}
Количество цифр в алфавите равно основанию системы счисления.
7

8.

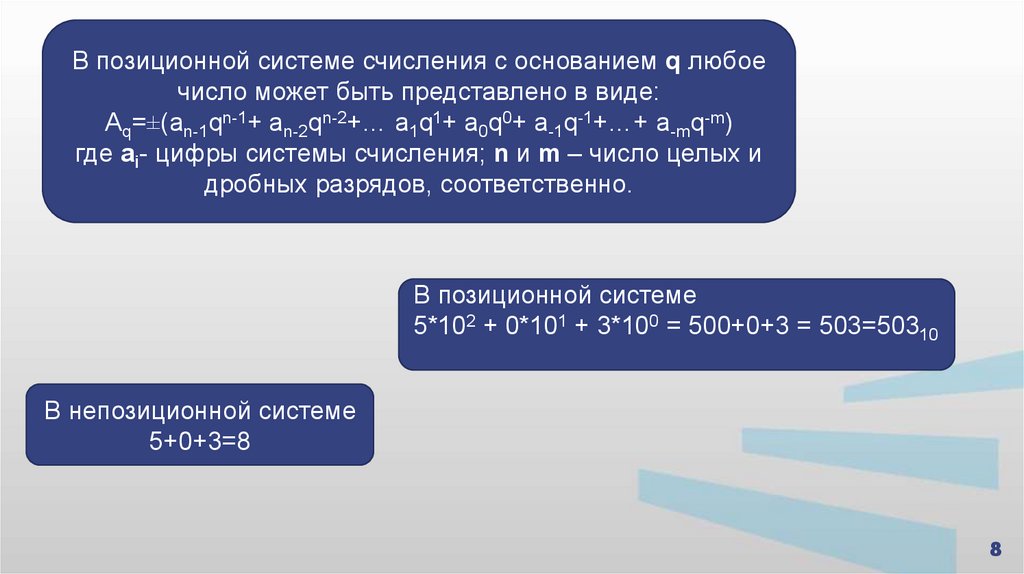
В позиционной системе счисления с основанием q любое
число может быть представлено в виде:
Аq=±(an-1qn-1+ an-2qn-2+… a1q1+ a0q0+ a-1q-1+…+ a-mq-m)
где ai- цифры системы счисления; n и m – число целых и
дробных разрядов, соответственно.
В позиционной системе
5*102 + 0*101 + 3*100 = 500+0+3 = 503=50310
В непозиционной системе
5+0+3=8
8

9.

Десятичная
Двоичная
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
Восьмеричная
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
Шестнадцатеричная
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
9

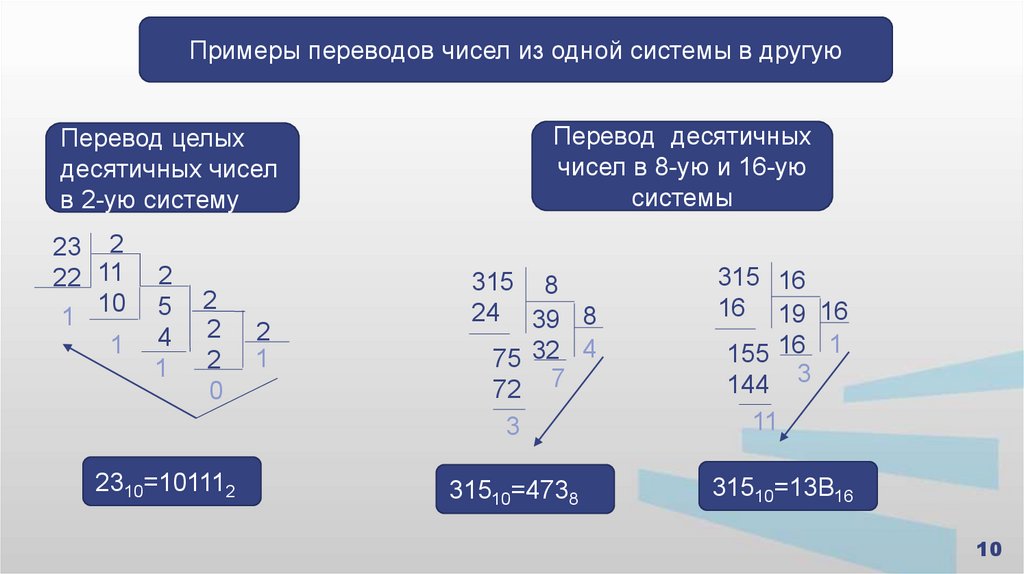
10.

Примеры переводов чисел из одной системы в другую
Перевод десятичных
чисел в 8-ую и 16-ую
системы
Перевод целых
десятичных чисел
в 2-ую систему
23 2
22 11
10
1
1
2
5
4
1
2
2
2
0
2310=101112
2
1
315 8
24 39 8
75 32 4
72 7
315 16
16 19 16
155 16 1
144 3
3
11
31510=4738
31510=13В16
10

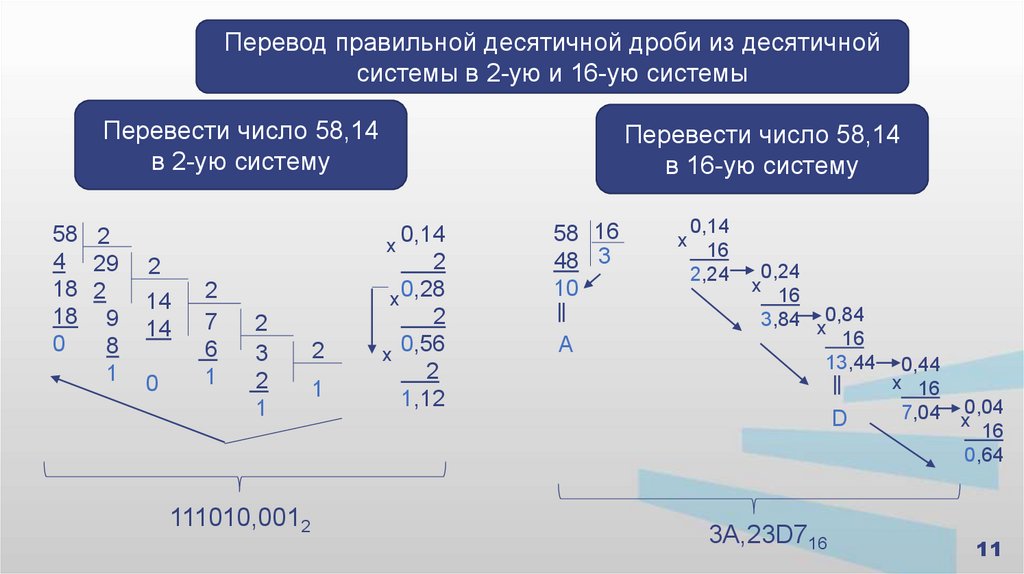
11.

Перевод правильной десятичной дроби из десятичной
системы в 2-ую и 16-ую системы
Перевести число 58,14
в 2-ую систему
58 2
4 29
18 2
18 9
0
8
1
Перевести число 58,14
в 16-ую систему
0,14
2
х 0,28
2
х 0,56
2
1,12
х
2
14
14
0
2
7
6
1
2
3
2
1
111010,0012
2
1
58 16
48 3
10
∥
А
х
0,14
16
2,24
0,24
х
16
3,84 х0,84
16
13,44
∥
D
3A,23D716
0,44
х 16
7,04
0,04
х
16
0,64
11

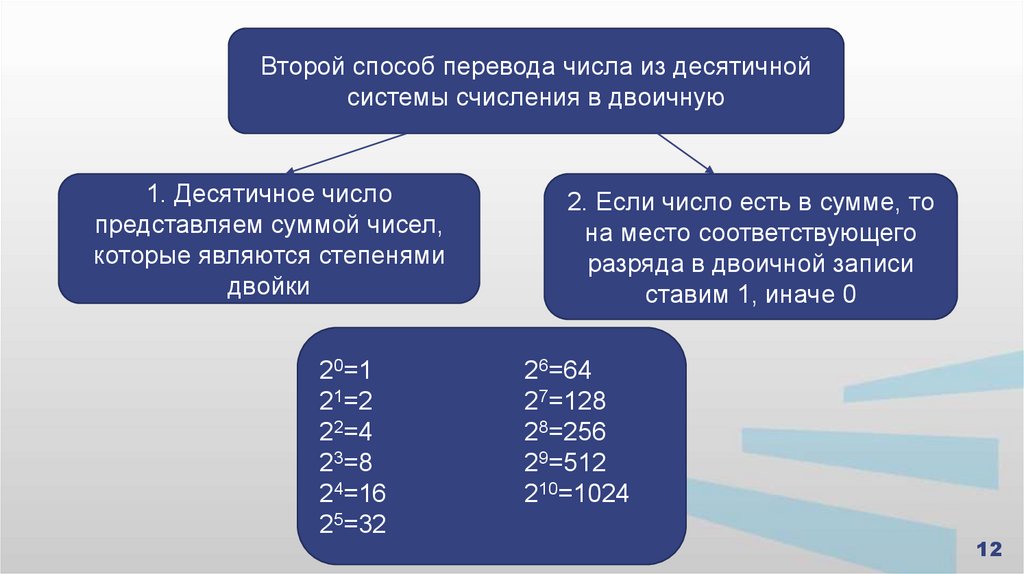
12.

Второй способ перевода числа из десятичной
системы счисления в двоичную
1. Десятичное число
представляем суммой чисел,
которые являются степенями
двойки
20=1
21=2
22=4
23=8
24=16
25=32
2. Если число есть в сумме, то
на место соответствующего
разряда в двоичной записи
ставим 1, иначе 0
26=64
27=128
28=256
29=512
210=1024
12

13.

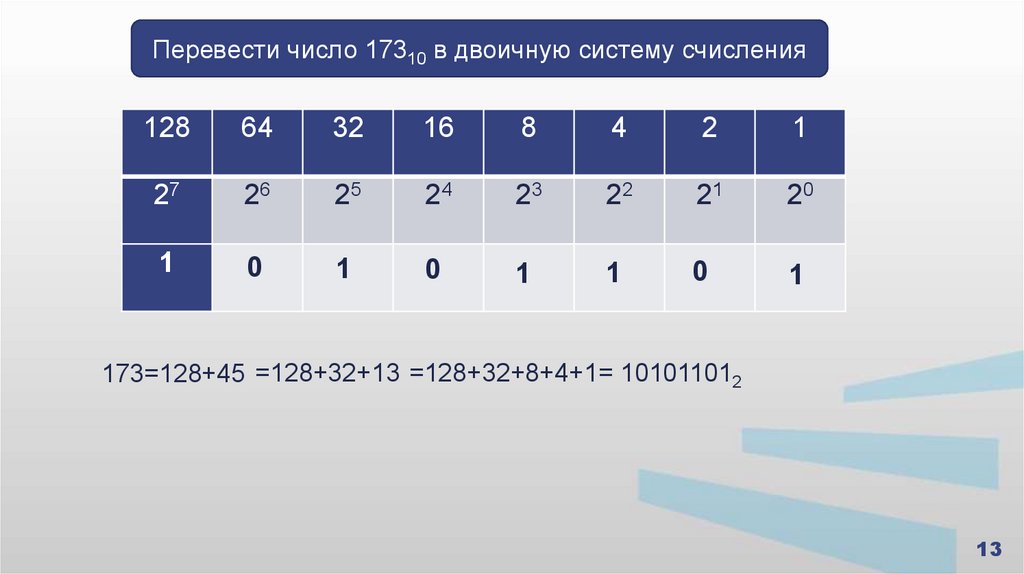
Перевести число 17310 в двоичную систему счисления
128
64
32
16
8
4
2
1
27
26
25
24
23
22
21
20
1
0
1
0
1
1
0
1
173=128+45 =128+32+13 =128+32+8+4+1= 101011012
13

14.

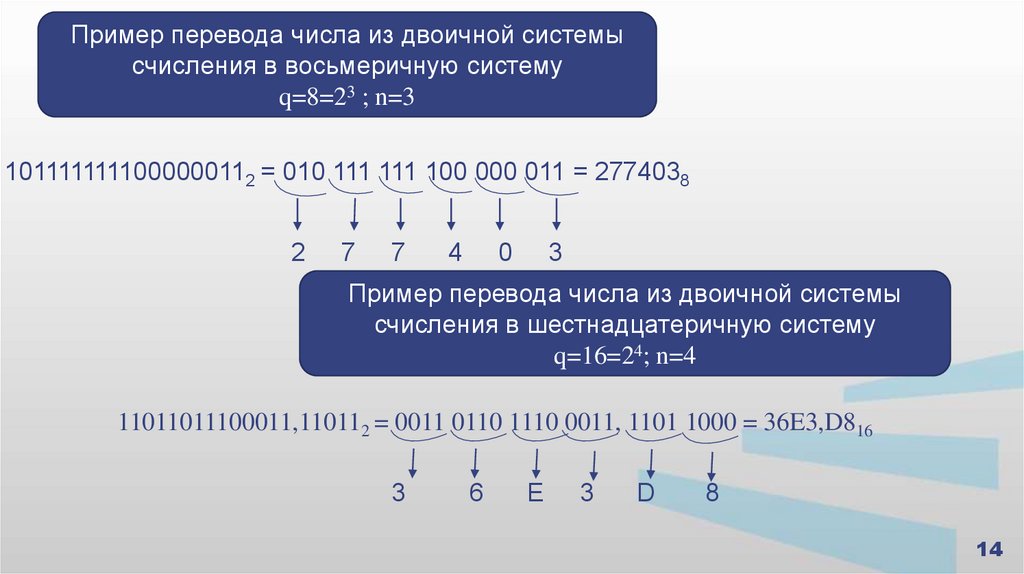
Пример перевода числа из двоичной системы
счисления в восьмеричную систему
q=8=23 ; n=3
1011111111000000112 = 010 111 111 100 000 011 = 2774038
2
7
7
4
0
3
Пример перевода числа из двоичной системы
счисления в шестнадцатеричную систему
q=16=24; n=4
11011011100011,110112 = 0011 0110 1110 0011, 1101 1000 = 36E3,D816
3
6
Е
3
D
8
14

15.

Построение в двоично-десятичной системе
Для записи цифры 0 используется код – 0000
Для записи цифры 1 используется код – 0001
Для записи цифры 2 используется код - 0010
Для записи цифры 3 используется код - 0011
Для записи цифры 4 используется код - 0100
Для записи цифры 5 используется код - 0101
Для записи цифры 6 используется код - 0110
Для записи цифры 7 используется код - 0111
Для записи цифры 8 используется код - 1000
Для записи цифры 9 используется код - 001
369110=0011 0110 1001 00012-10
1000 0000 0111 00102-10 = 807210
15

16.

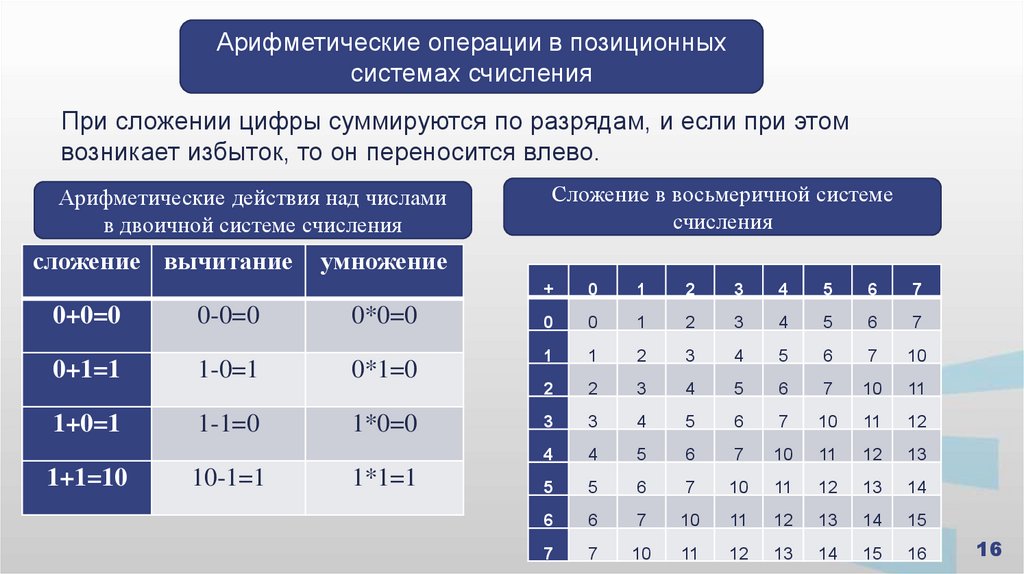
Арифметические операции в позиционных
системах счисления
При сложении цифры суммируются по разрядам, и если при этом
возникает избыток, то он переносится влево.
Арифметические действия над числами
в двоичной системе счисления
сложение вычитание
умножение
0+0=0
0-0=0
0*0=0
0+1=1
1-0=1
0*1=0
1+0=1
1-1=0
1*0=0
1+1=10
10-1=1
Сложение в восьмеричной системе
счисления
1*1=1
+
0
1
2
3
4
5
6
7
0
0
1
2
3
4
5
6
7
1
1
2
3
4
5
6
7
10
2
2
3
4
5
6
7
10
11
3
3
4
5
6
7
10
11
12
4
4
5
6
7
10
11
12
13
5
5
6
7
10
11
12
13
14
6
6
7
10
11
12
13
14
15
7
7
10
11
12
13
14
15
16
16

17.

Сложим числа 15 и 6 в различных системах счисления.
Двоичная:11112+1102 Восьмеричная: 178+68
111
+
1111
0110
10101
1+0=1
1+1=2=2+0
1+1+1=3=2+1
1+1=2=2+0
+
Шестнадцатеричная: F16+616
17
6
25
F
+6
15
7+6=13=8+5
15+6=21=16+5
1+1=2
Ответ: 15+6=2110=101012=258=1516
Проверка: преобразуем полученные суммы к десятичному виду:
101012=24+22+20=16+4+1=21,
258=2·81+5·80=16+5=21,
1516=2·161+5·160=16+5=21.
17

18.

Сложим числа 15, 7 и 3 в различных системах счисления
Десятичная: 1510+710+310
Восьмеричная:178+78+38
Двоичная: 11112+1112+112
11+1 1
1
17
+ 7
3
31
15
+ 7
3
25
5+7+3=15=10+5
1+1=2
Шестнадцатеричная: F16+716+316
1111
+ 111
11
11001
7+7+3=17=2*8+1
1+1+1=3=2+1
1+1+1+1=4=2*2+0
1+1=2=2+0
1+1+1=3=2+1
2+1=3
F
+ 7
3
19
15+7+3=25=16+9
18

19.

Сложим числа 141,5 и 59,75 в двоичной системе счисления
1. Переведем числа в двоичную систему
141 2
140 70 2
1 6
35
10 2
10 15
0 14
1
х
2
17
16
1
2
8
8
0
0,5
2
1,0
2
4 2
4 2 2
0 2 1
0
10001101,12
19

20.

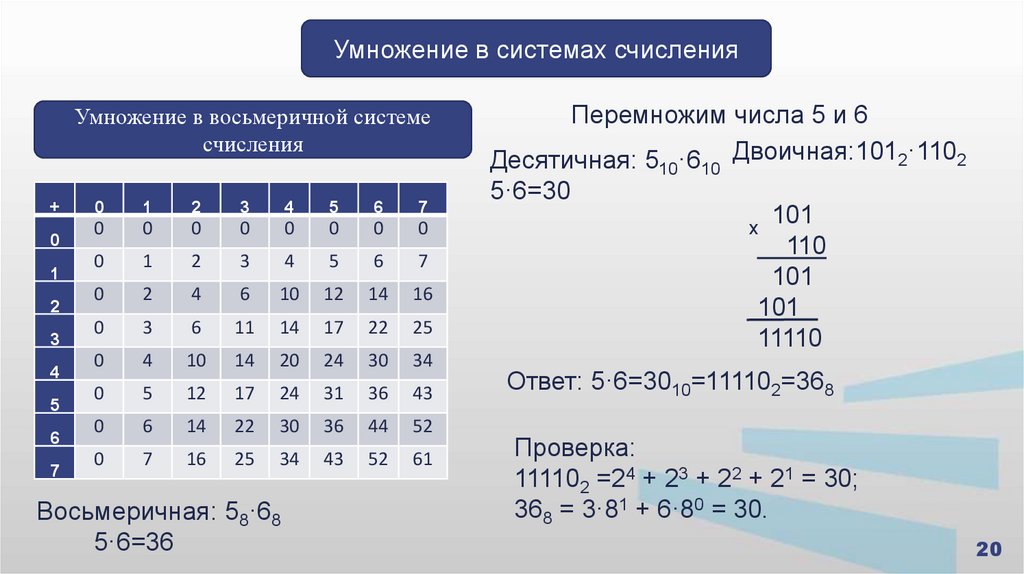
Умножение в системах счисления
Умножение в восьмеричной системе
счисления
+
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
0
2
4
6
10
12
14
16
0
3
6
11
14
17
22
25
0
4
10
14
20
24
30
34
0
5
12
17
24
31
36
43
0
6
14
22
30
36
44
52
0
7
16
25
34
43
52
61
Восьмеричная: 58·68
5·6=36
Перемножим числа 5 и 6
Десятичная: 5 ·6 Двоичная:1012·1102
5·6=30
10
10
101
110
101
101
11110
х
Ответ: 5·6=3010=111102=368
Проверка:
111102 =24 + 23 + 22 + 21 = 30;
368 = 3·81 + 6·80 = 30.
20

21.

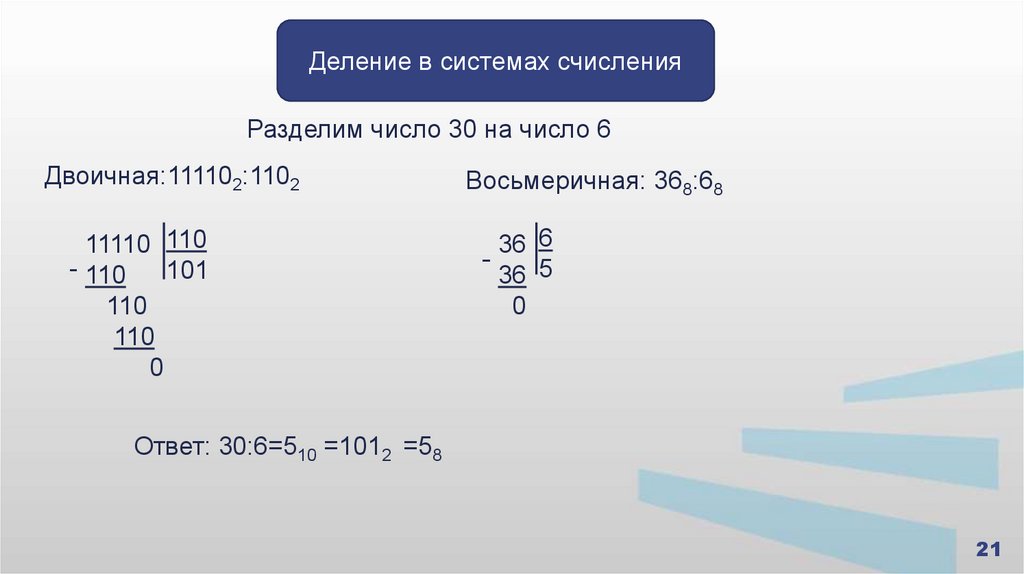
Деление в системах счисления
Разделим число 30 на число 6
Двоичная:111102:1102
11110 110
- 110
101
110
110
0
Восьмеричная: 368:68
36 6
36 5
0
Ответ: 30:6=510 =1012 =58
21

22.

22

23.

Спасибо за внимание
23