Системы счисления

1. Лекция № 1. Системы счисления

ИНФОРМАТИКА
Лекция № 1.
Системы счисления
1

2. Определение системы счисления

Определение № 1.
Набор символов, правил счета и записи чисел в
виде последовательности символов из этого
набора образуют систему счисления. Набор
символов системы счисления называется
алфавитом, а сами символы - цифрами.
2

3. Непозиционные системы счисления

Определение № 2.
В
непозиционных
системах
счисления
количественное значение цифры зависит только от ее
вида, а в некоторых непозиционных системах
счисления (например, римской) - от взаимного
расположения цифр.
3

4. Позиционные системы счисления

Определение № 3.
В позиционных системах счисления вес цифры в
записи числа зависит от ее вида и от занимаемой ею
позиции. Позиции цифр в таких системах счисления
называются разрядами.
Собственным весом цифры назовем значение
одноразрядного числа записанного только с помощью
этой одной цифры.
4

5. Основание системы счисления

Определение № 4.
Число q, равное количеству различных цифр в
алфавите позиционной системы счисления,
называется основанием системы счисления.
В алфавите арабской системы счисления q равно
десяти, так как алфавит включает в себя десять
различных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В
соответствии со значением основания арабскую
систему
счисления
называют
десятичной
системой счисления.
5

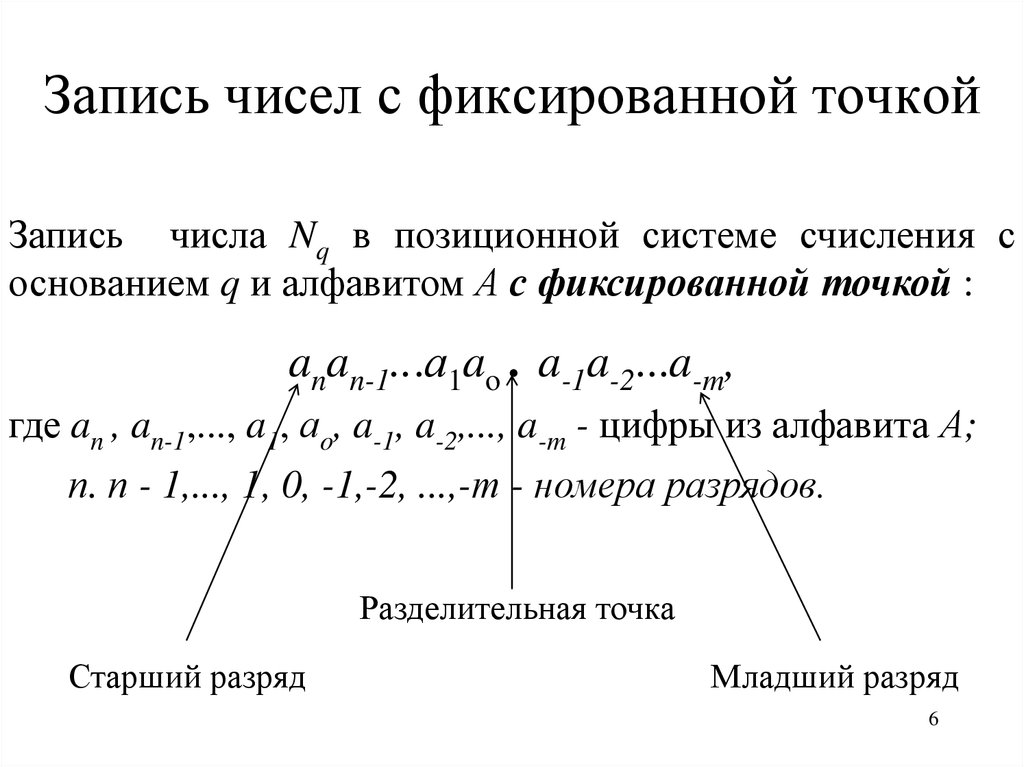
6. Запись чисел с фиксированной точкой

Запись числа Nq в позиционной системе счисления с
основанием q и алфавитом А с фиксированной точкой :
anan-1...а1ao . a-1a-2...a-m,
где an , an-1,..., a1, аo, a-1, a-2,..., a-m - цифры из алфавита А;
п. п - 1,..., 1, 0, -1,-2, ...,-т - номера разрядов.
Разделительная точка
Старший разряд
Младший разряд
6

7. Запись чисел с фиксированной точкой. Определения 5-7.

5. Разряды с номерами, которые больше или равны
нуля, образуют целую часть числа. Разряды с
номерами, меньшими нуля, образуют дробную часть
числа. В записи числа эти части числа отделяются
разделительной (дробной) точкой.
6. Если дробная часть отсутствует, то число
называют целым и опускают разделительную точку в
записи числа.
7. Если отсутствует целая часть, то число называют
правильной дробью и перед разделительной точкой
записывают ноль.
7

8. Запись чисел с плавающей точкой

Запись числа Nq в позиционной системе счисления с
основанием q и алфавитом А с плавающей точкой :
anan-1...а1ao . a-1a-2...a-m qk,
где an , an-1,..., a1, аo, a-1, a-2,..., a-m - цифры алфавита А;
п, п - 1,..., 1, 0, -1, -2, ..., -т - номера разрядов,
k – абсолютный порядок числа.
Пример: 0.035 1099 = 0.35 1098= 0.0035 10100.
8

9. Применение систем счисления в ЭВМ

Двоичная система счисления имеет алфавит, состоящий
только из двух цифр: 0 и 1.
Основанием двоичной системы счисления является число два.
Восьмеричная система счисления имеет алфавит из восьми
цифр:0, 1, 2, 3, 4, 5, 6, 7.
Основанием восьмеричной системы является число восемь.
Десятичная система счисления имеет алфавит, состоящий
только из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Основанием двоичной системы счисления является число
десять.
Шестнадцатеричная система счисления имеет алфавит из
шестнадцати цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f.
Основанием шестнадцатеричной системы счисления является
число шестнадцать.
9

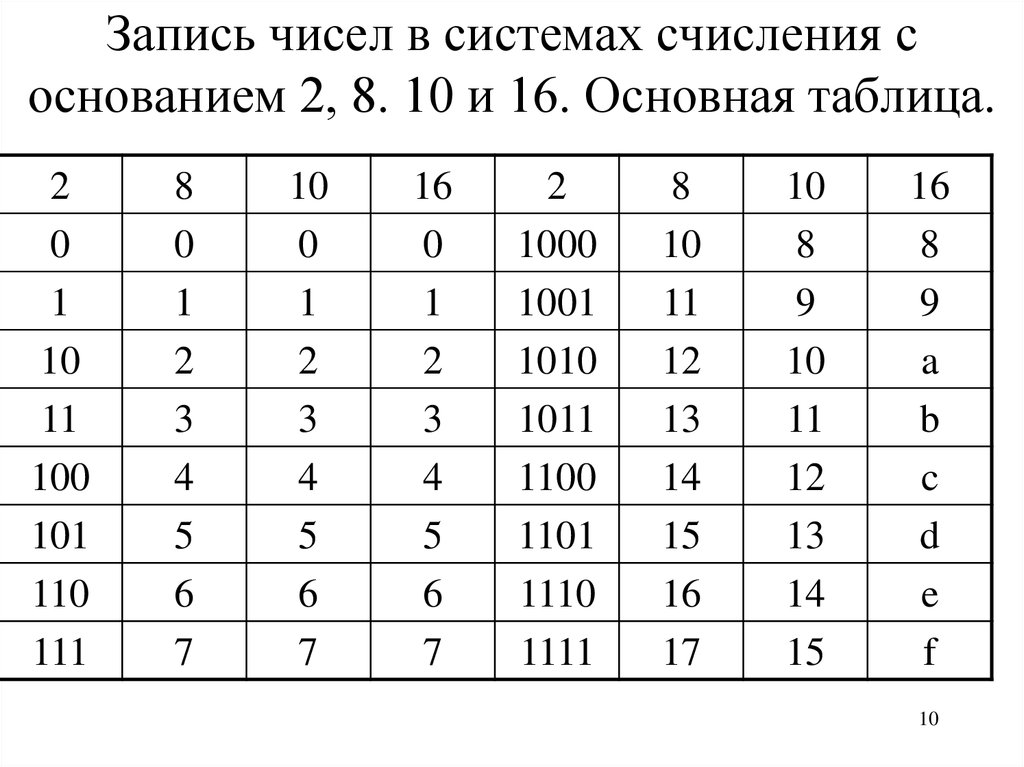
10. Запись чисел в системах счисления с основанием 2, 8. 10 и 16. Основная таблица.

2
0
1
10
11
100
101
110
111
8
0
1
2
3
4
5
6
7
10
0
1
2
3
4
5
6
7
16
0
1
2
3
4
5
6
7
2
1000
1001
1010
1011
1100
1101
1110
1111
8
10
11
12
13
14
15
16
17
10
8
9
10
11
12
13
14
15
16
8
9
a
b
c
d
e
f
10

11. Перевод чисел из одной СС в другую СС

8
1
2
1
4
3
10
2
2
2
1
3
4
16
11

12. Пример перевода из двоичной СС

Выполнить перевод числа 1011012 из двоичной системы
счисления в десятичную систему счисления:
543210
1011012 = 1 25 + 0 24 + 1 23 +1 22 + 0 21 +1 20 =
= 32 + 0 + 8 + 4 + 0 + 1 = 4510.
12

13. Проверка решения. Перевод из десятичной СС в двоичную СС

Проверим результат перевода:
45:2 = 22 (1);
22:2 = 11 (0);
11:2 = 5 (1);
5:2 = 2 (1);
2:2 = 1 (0).
Запишем число в двоичной системе счисления:
4510 = 1011012.
Проверка подтверждает правильность решения.
Ответ: 1011012 = 4510.
13

14. Перевод из шестнадцатеричной системы счисления в десятичную систему счисления

Выполнить перевод числа 1dc16 из шестнадцатеричной системы
счисления в десятичную систему счисления.
2 10
1dc16 = 1 162 + 13 161 +12 160 = 256+208+12 = 47610.
Проверим результат перевода:
1.)
476:16 = 29 (12);
2.)
29:16 =
1 (13).
Запишем число в шестнадцатеричной системе счисления: 47610=
1dc16. Проверка подтверждает правильность решения.
Ответ: 1dc16 = 47610.
14

15. Пример перевода чисел из двоичной СС в восьмеричную СС

Выполнить перевод числа 1011112 из двоичной системы
счисления в восьмеричную систему счисления:
Разобьем исходную запись числа на триады двоичных разрядов:
101111 101 111.
Поставим в соответствие каждой триаде восьмеричную цифру:
1012 58;
1012 78.
Запишем число: 1011112 = 578.
15

16. Проверка решения. Перевод из восьмеричной СС в двоичную СС

Проверим результат перевода:
Поставим в соответствие каждой восьмеричной цифре триаду:
58 1012;
7 1112;
Запишем число: 578 = 1011112.
Проверка подтверждает правильность решения.
Ответ: 1011112 = 578.
16

17. Пример перевода дробных чисел

Перевести 17.9710 из десятичной системы счисления в
восьмеричную систему счисления
и обратно
из полученного представления числа
в
десятичную
систему
счисления.
Перевод
производить с точностью до 3 знаков.
Сравнить результаты, полученные после «обратного»
перевода в десятичную систему счисления с
исходным
десятичным
числом.
Определить
относительную ошибку перевода.
17

18. Перевод в восьмеричную систему

1. Выполним перевод числа 17.97 из десятичной системы
счисления в восьмеричную систему счисления.
1.1.
Переводим целую часть числа:
1)
17 : 8 = 2 (1), 2 < 8 – конец перевода.
Итак, 1710 = 218
1.2.
Переводим дробную часть числа:
1)
0.97 8 = 7.76 (7);
2)
0.76 8 = 6.08 (6);
3)
0.08 8 = 0.64 (0);
Итак, 0.9710 = 0.7608
Таким образом, 17.9710 = 21.7608
18

19. Перевод из восьмеричной в десятичную систему

Выполним перевод числа 21.760 из восьмеричной системы
счисления в десятичную систему счисления.
1 0 -1-2-3
21.7608 = 2 81 + 1 80 + 6 8-2 + 0.8-3 = 16 + 1 + 0.875 +
0.09375 + 0 = 17.9687510.
Запишем искомое число: 21.7608 = 17.9687510
Имеем: 17.970 ≠ 17.96875.
19

20. Определение относительной ошибки

Вычислим относительную ошибку :
( N 10 N 10)
(17.970 17.96875)
*100%
*100% 0.0069%
N 10
17.970
20