Системы счисления

1.

Информатика
Системы счисления
Представление чисел в различных
системах счисления.
Операции над числами в различных
системах счисления
Элементы теории
www.learn.knastu.ru

2.

Информатика
Оглавление
1 Общие сведения о системах счисления
2 Позиционные системы счисления. Основные понятия
3 Представление чисел в позиционных системах счисления.
Общая формула. Перевод из одной системы счисления в другую
3.1 Десятичная система счисления
3.2 Двоичная система счисления
3.3 Восьмеричная система счисления
3.4 Шестнадцатеричная система счисления
3.5 Троичная система счисления
4 Арифметические операции над числами в различных системах
счисления
4.1 Операции над числами в двоичной системе счисления
4.2 Операции над числами в произвольной системе счисления
Системы счисления. Элементы теории
www.learn.knastu.ru

3.

Информатика
1 Общие сведения о системах счисления
Для записи информации о количестве объектов материального
мира используются числа.
Числа записываются с использованием символов, которые называются
цифрами.
Система счисления - знаковая система, состоящая из цифр и
определенных правил записи чисел.
Все используемые в данной системе счисления цифры составляют ее
алфавит.
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории

4.

1 Общие сведения о системах счисления
Информатика
Системы счисления
Позиционные
Непозиционные
Значение числа в позиционной
системе счисления определяется как
цифрами, принятыми в системе, так и
положением (позицией) этих цифр в
числе.
25
52
520
502
XXVII = 10+10+5+1+1
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории

5.

Информатика
2 Позиционные системы счисления.
Основные понятия
Основание системы счисления - это целое положительное число, большее 1 и
равное максимальному количеству различных символов, употребляемых в данной
системе счисления.
В частности, для десятичной системы счисления
0 1 2 3 4 5 6 7 8 9
Основание равно 10.
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории

6.

Информатика
3 Представление чисел в позиционных системах счисления
3.1 Десятичная система счисления
123
Запись числа
1
2
3
Номер разряда
3
2
1
Значение
102
101
100
A = an+1 10n + an 10n–1 + ... + a1 100
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории

7.

Информатика
3 Представление чисел в позиционных системах счисления
3.2 Общая формула записи числа в позиционной системе счисления с
произвольным целым основанием
Обозначения:
q – основание системы счисления,
ai - любая цифра из алфавита системы счисления (вес разряда).
i - номер позиции, занимаемой цифрой (разряд).
Запись числа А
an+1
an
…
a2
a1
Номер разряда
n+1
n
…
2
1
Значение
qn
qn-1
…
q1
q0
Aq = an+1qn + an qn–1 + ... + a2q1 +a1q0
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории

8.

Информатика
3 Представление чисел в позиционных системах счисления
3.3 Двоичная система счисления
Цифры - 0, 1.
Запись числа А
an+1
an
…
a2
a1
Номер разряда
n+1
n
…
2
1
Значение
2n
2n-1
…
21
20
Разряд
1
20
n
n–1
1
0
A2 = an+12 + an 2 + ... + a22 +a12 2
20
3
20
4
20
510 = 1*22+0*21 +1*20 = 1012
5
20
6
20
7
20
Вес
1
2
4
8
16
32
64
Разряд
8
20
9
20
10
20
11
20
12
20
13
20
…
…
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории
Вес
128
256
512
1024
2048
4096
…

9.

Информатика
3 Представление чисел в позиционных системах счисления
3.3 Двоичная система счисления
Перевод чисел из десятичной СС в двоичную
Для перевода числа из десятичной СС в двоичную исходное десятичное число
многократно (до тех пор, пока частное не станет равным нулю) делится на основание
двоичной системы, т.е. на 2. Если при делении образуется остаток, то в
соответствующий двоичный разряд записывается 1, если делится без остатка, то
записывается 0. Запись остатков в двоичное число ведется слева направо, т.е. от
младшего разряда к старшим.
www.learn.knastu.ru
www.learn.knastu.ru
Системы счисления. Элементы
теории

10.

Информатика
3 Представление чисел в позиционных системах счисления
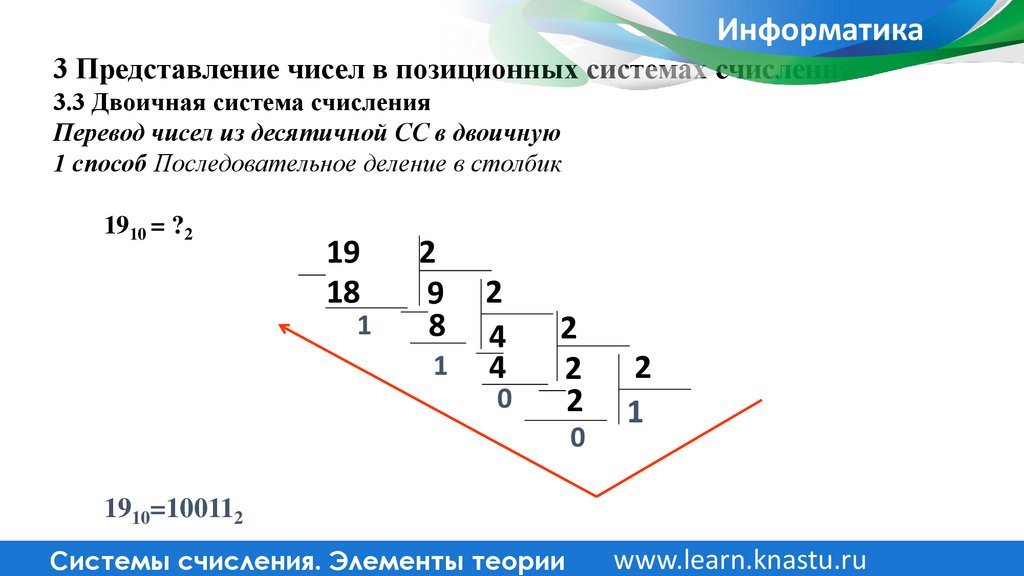
3.3 Двоичная система счисления
Перевод чисел из десятичной СС в двоичную
1 способ Последовательное деление в столбик
1910 = ?2
19
18
1
2
9
8
1
2
4
4
0
2
2
2
0
2
1
1910=100112
Системы счисления. Элементы теории
www.learn.knastu.ru

11.

Информатика
3 Представление чисел в позиционных системах счисления
3.3 Двоичная система счисления
Перевод чисел из десятичной СС в двоичную
2 способ Последовательное деление
1910 = ?2
19 : 2 = 9 (остаток 1)
9 : 2 = 4 (остаток 1)
4 : 2 = 2 (остаток 0)
2 : 2 = 1 (остаток 0)
1 : 2 = 0 (остаток 1)
1910=100112
Системы счисления. Элементы теории
www.learn.knastu.ru

12.

Информатика
3 Представление чисел в позиционных системах счисления
3.3 Двоичная система счисления
Перевод чисел из десятичной СС в двоичную
3 способ Подбор
1910 = ?2
1910 = 16 + 2 + 1 = 24 + 21 + 20 = 100112
Разряд
1910=100112
Вес
Разряд
Вес
1
20
1
8
20
128
2
20
2
9
20
256
3
20
4
10
20
512
4
20
8
11
20
1024
5
20
16
12
20
2048
6
20
32
13
20
4096
7
20
64
…
…
…
Системы счисления. Элементы теории
www.learn.knastu.ru

13.

Информатика
3 Представление чисел в позиционных системах счисления
3.3 Двоичная система счисления
Перевод чисел из двоичной СС в десятичную
Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы
произведений степеней числа 2 (основания двоичной системы счисления) на соответствующие
цифры в разрядах двоичного числа.
100112 = 1*20 + 1*21 + 0*22 + 0*23 + 1*24 = 1+ 2 + 16 = 1910.
Системы счисления. Элементы теории
www.learn.knastu.ru

14.

Информатика
3 Представление чисел в позиционных системах счисления
3.3 Двоичная система счисления
Системы счисления. Элементы теории
www.learn.knastu.ru

15.

Информатика
3 Представление чисел в позиционных системах счисления
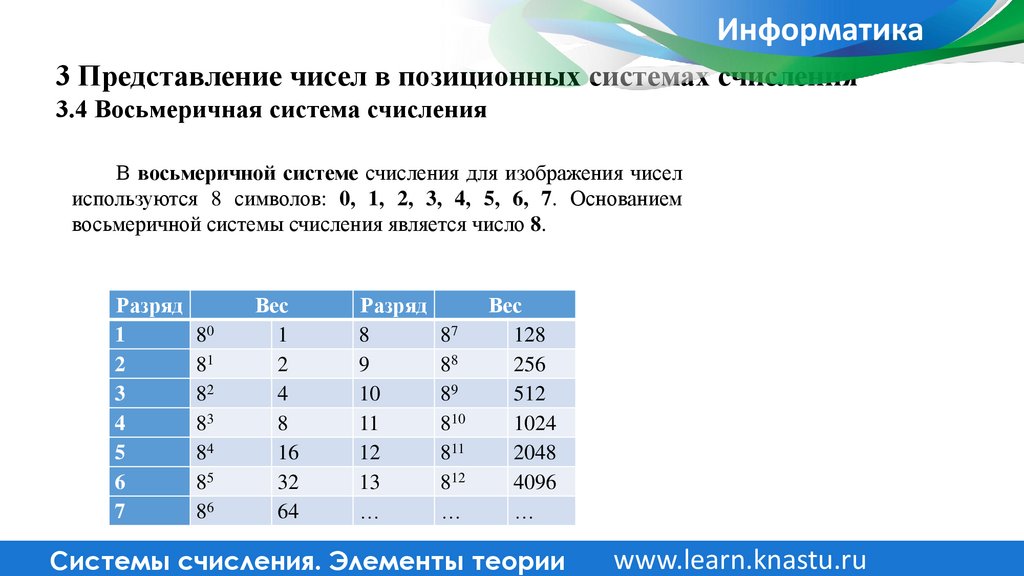
3.4 Восьмеричная система счисления
В восьмеричной системе счисления для изображения чисел
используются 8 символов: 0, 1, 2, 3, 4, 5, 6, 7. Основанием
восьмеричной системы счисления является число 8.
Разряд
1
80
2
81
3
82
4
83
5
84
6
85
7
86
Вес
1
2
4
8
16
32
64
Разряд
8
87
9
88
10
89
11
810
12
811
13
812
…
…
Вес
128
256
512
1024
2048
4096
…
Системы счисления. Элементы теории
www.learn.knastu.ru

16.

Информатика
3 Представление чисел в позиционных системах счисления
3.4 Восьмеричная система счисления
Перевод десятичного числа в 8-ричную системы счисления
Для перевода числа из десятичной СС в восьмеричную исходное десятичное число
многократно (до тех пор, пока частное не станет равным нулю) делится на основание
двоичной системы, т.е. на 8. Если при делении образуется остаток, то он записывается в
соответствующий разряд, если делится без остатка, то записывается 0. Запись остатков в
восьмеричное число ведется слева направо, т.е. от младшего разряда к старшим.
478410 = 112608
Системы счисления. Элементы теории
www.learn.knastu.ru

17.

Информатика
3 Представление чисел в позиционных системах счисления
3.4 Восьмеричная система счисления
Перевод 8-ричного числа в десятичную систему счисления
Для преобразования чисел из восьмеричной системы счисления в десятичную
необходимо записать число в полной форме и вычислить его значение.
6758=?10
6758 = 6*82+7*81+5*80= 6*64+7*8+5*1=44510
Системы счисления. Элементы теории
www.learn.knastu.ru

18.

Информатика
3 Представление чисел в позиционных системах счисления
3.4 Восьмеричная система счисления
Перевод 8-ричного числа в двоичную систему счисления
Для преобразования чисел из восьмеричной системы счисления в
двоичную необходимо каждую цифру исходного восьмеричного
числа перевести в двоичную систему счисления и в том же порядке
записать полученные числа вместе.
7518=?
78=1112
58=0112
18=0012
7518=111 011 0012
Системы счисления. Элементы теории
www.learn.knastu.ru

19.

Информатика
3 Представление чисел в позиционных системах счисления
3.4 Восьмеричная система счисления
Перевод 2-ичного числа в 8-ричную систему счисления
Для преобразования числа из двоичной системы счисления в
восьмеричную необходимо каждую цифру исходного восьмеричного
числа перевести в двоичную систему счисления и в том же порядке
записать полученные числа вместе.
110010011112 = ?8
011.001.001.1112
0112 = 38
0012 = 18
0012 = 18
1112 = 78
110010011112 = 31178
Системы счисления. Элементы теории
www.learn.knastu.ru

20.

Информатика
.
.
Спасибо за внимание!
Системы счисления. Элементы теории
www.learn.knastu.ru