Системы счисления. Что такое система счисления?

1.

Системы счисления
СУХАЧЕВА ВАЛЕРИЯ АРТЕМОВНА,
УЧИТЕЛЬ ИНФОРМАТИКИ
ГБОУ СОШ № 79

2.

Вспомним
Что такое система счисления?
Какие системы счисления вы знаете?
Что такое позиционная сс?
Что такое непозиционная сс?

3.

Основные понятия систем счисления
Система счисления - это способ записи (представления) чисел.
Число - это некоторая величина
Цифра - это символы, участвующие в записи числа
Алфавит - совокупность различных цифр, используемых для записи числа

4.

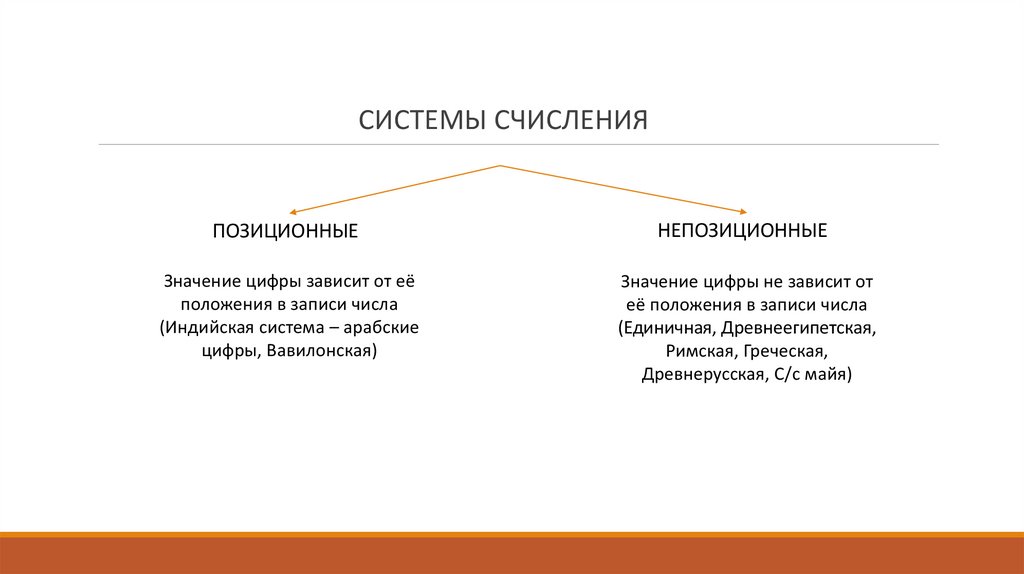
СИСТЕМЫ СЧИСЛЕНИЯ
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
Значение цифры зависит от её
положения в записи числа
(Индийская система – арабские
цифры, Вавилонская)
Значение цифры не зависит от
её положения в записи числа
(Единичная, Древнеегипетская,
Римская, Греческая,
Древнерусская, С/с майя)

5.

Позиционные системы счисления
В таблице показана связь между основанием системы счисления, ее названием и
алфавитом.
Основание
(количество цифр)
При q > 10 к
десяти арабским
цифрам
добавляют
латинские буквы.
Система счисления
Алфавит (все цифры)
q=10
десятичная
0,1,2,3,4,5,6,7,8,9
q=2
двоичная
0,1
q=3
троичная
0,1,2
q=5
пятеричная
0,1,2,3,4
q=8
восьмеричная
0,1,2,3,4,5,6,7
q=11
одиннадцатеричная
0,1,2,3,4,5,6,7,8,9,A
q=13
тринадцатеричная
0,1,2,3,4,5,6,7,8,9,A,B,C
q=16
шестнадцатеричная
0,1,2,3,4,5,6,7,8,9,A,B,C,D
,E,F

6.

Основная формула
В позиционной системе счисления с основанием q любое число может быть
представлено в виде:
Aq =±(an–1 qn–1+ an–2 qn–2+…+ a0 q0+ a–1 q–1+…+ a–m q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.

7.

Десятичная система счисления
Десятичная система счисления — позиционная система счисления по
целочисленному основанию 10.
Предполагается, что основание 10 связано с количеством пальцев на руках
у человека.

8.

Двоичная система счисления
В архитектуре компьютера все биты должны быть заполнены либо нолями
либо единицами.
Двоичной системой счисления называется позиционная система счисления
с основанием 2.
Двоичный алфавит: 0 и 1.

9.

Перевод из 10сс в 2сс
1. Разделить целое десятичное число на 2. Остаток записать.
2. Если полученное частное не меньше 2, то продолжать деление.
3. Двоичный код десятичного числа получается при последовательной
записи последнего частного и всех остатков, начиная с последнего.
Получилось:3510 = 1000112

10.

Задание
Перевести из 10сс в 2сс:
• 127
• 103
• 46

11.

Перевод из 2сс в 10сс
Для целых двоичных чисел можно записать:
an–1an–2…a1a0 = an–1 2n–1 + an–2 2n–2 +…+ a0 20
Пример:
10010112 = 1∙26+0∙25+0∙24+1∙23+0∙22+1∙21+1∙20 = 64+0+0+8+0+2+1 = 7510

12.

Задание
Перевести из 10сс в 2сс:
•10010
•111
•10100001

13.

Домашнее задание
Перевести из 10 сс в 2 сс: 89, 64, 37
Перевести из 2 сс в 10 сс: 1001, 1101101, 1111

14.

Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система
счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80

15.

Перевод из 10сс в 8сс
Для перевода целого десятичного числа в восьмеричную систему счисления
следует последовательно выполнять деление данного числа и получаемых
целых частных на 8 до тех пор, пока не получим частное, равное нулю.
19210 = 3008

16.

Задание
Перевести из 8сс в 10сс:
• 23
•467
•88

17.

Перевод из 8сс в 10сс
Для перевода целого восьмеричного числа в десятичную систему счисления
следует перейти к его развёрнутой записи и вычислить значение
получившегося выражения.
10638 =1 83 +0 82+6 81+3 80=56310

18.

Задание
Перевести из 10сс в 8сс:
• 92
• 145
•13

19.

Шестнадцатеричная система
счисления
Шестнадцатеричная система счисления — позиционная система
счисления по основанию 16.
В качестве цифр этой системы счисления обычно используются цифры от 0
до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 1010,
1110, 1210, 1310, 1410, 1510 соответственно.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

20.

Перевод из 10сс в 16сс
Для перевода числа из позиционной системы счисления по
целосчислительному основанию 10 в позиционную целочисленную систему
счисления с основанием 16, потребуется поделить его на 16, до того
момента, когда окончательный результат не будет меньше или равен 16.
13810 = 8A16

21.

Задание
Перевести из 10сс в 16сс:
• 397
•467
•88

22.

Перевод из 16сс в 10сс
Число в позиционной целочисленной системе счисления с основанием 16
представляется, как последовательность цифр финального деления и
остатков от деления в обратном порядке.
3АF16 =3 162+10 161+15 160 =768+160+15=94310

23.

Задание
Перевести из 16сс в 10сс:
• 12C
•125
•88

24.

Домашнее задание
Переведите числа из десятичной системы счисления в двоичную,
восьмеричную и шестнадцатеричную системы счисления.
•563
•264
• 234
•53
•2861