ЛЕКЦИЯ_5 (2)

1.

СТАТИКА
1. Предмет статики
Статика – это раздел теоретической механики, который изучает методы преобразования
систем сил в эквивалентные системы и устанавливает необходимые и достаточные условия
равновесия тел под действием сил.
В статике рассматриваются постоянные силы, но законы сложения сил и приведения их к
простейшему виду, полученные в статике, справедливы и для переменных сил.
Под равновесием понимается состояние покоя тела или его равномерное прямолинейное
движение по отношению к другим телам.
В первом случае a=0 и V=0, во втором случае a=0, V=const. И в первом и во втором случае
ΣFk=0.
Если движением тела по отношению к которому рассматривается равновесие данного тела
можно пренебречь, то равновесие называют абсолютным, в противном случае – относительным.
Задачи статики:
1.
Преобразование систем сил в эквивалентные системы;
2.
Установление необходимых и достаточных условий равновесия тел под действием сил.
2. Сила
Сила – это векторная величина, являющаяся количественной мерой механического
взаимодействия материальных тел.
Основной единицей измерения силы является ньютон (1 кГ= 9,81Н).
Cила – как любая векторная величина определяется: 1) модулем силы; 2) точкой приложения
силы; 3) направлением.
Под действием сил тело может совершать поступательное, вращательное или сложное движение,
которое можно представить как сумму поступательного и вращательного движений.
В общем случае классификацию сил можно представить в виде

2.

Внешними называются силы Fe, действующие на
частицы данного тела со стороны других материальных
тел, не принадлежащих системе.
СИЛЫ
СОСРЕДОТОЧЕННЫЕ
В
Н
Е
Ш
Н
И
Е
Fe
РАСПРЕДЕЛЕННЫЕ
АКТИВНЫЕ
РЕАКТИВНЫЕ
В
Н
У
Т
Р
Е
Н
Н
И
Е
Fi
Внутренними называются силы Fi, с которыми
частицы данного тела действуют друг на друга.
Активные силы Fa – это силы значение и
направление, которых не зависит от других сил,
действующих на тело.
Реактивные силы Fr – это силы значение и
направление, которых зависит от активных сил,
действующих на тело.
Если активные силы, действующие на твердое
тело равны нулю, то и реактивные силы равны
нулю.
Сосредоточенными называются силы, приложенные к точке.
Распределенными называются силы, которые распределены, вдоль какой либо линии, либо
поверхности и характеризуются интенсивностью распределенной нагрузки q, т.е. величиной,
приходящейся на единицу длинны (площади) нагруженного элемента.
Единицей измерения является ньютон, деленный на метр [Н/м] (ньютон, деленный на метр в
квадрате [Н/м2]).
При решении задач распределенные силы заменяют сосредоточенной равнодействующей силой
Q, которая приложена в центре тяжести эпюры нагружения.
Некоторые примеры распределенных нагрузок.

3.

1. Силы равномерно распределены вдоль
балки длины l
2. Силы распределены по линейному закону
вдоль балки длины l
l
l
Q lq
С
q
1
Q lq
2
q
С
1
3l
Q
0.5l
Q
3. Система сил
Состояние равновесия или движения тела зависит от характера его взаимодействия с другими
телами, мерой этого взаимодействия является сила.
Направление и точка приложения силы зависит от характера взаимодействия и от взаимного
расположения объектов.
Совокупность сил, действующих на тело, называется системой
сил (F1, F2, F3, …, Fn).
Две системы называются эквивалентными одна другой, если
каждая из них, действуя отдельно, сообщает телу одно и тоже действие
(F1, F2, F3, …, Fn)≡(Φ1, Φ 2, Φ 3,…, Φ n).
F4
z
F5
F3
F6
F2
Система сил эквивалентна нулю или уравновешена, если она,
будучи приложенной к телу, не изменяет его состояние F1
x
(F1, F2, F3,…, Fn)≡0.
F7
y
O
Fn
Fk
F8

4.

Если система сил эквивалентна одной силе R, т. е. (F1, F2, F3, …, Fn)≡R, R – есть
равнодействующая данной системы сил, то данная система сил может быть заменена одной
равнодействующей силой.
Силу R называют уравновешивающей, если она, будучи приложенной, к данной системе,
составляет вместе с ней новую систему сил, эквивалентную нулю.
Данная система сил (F1, F2, F3, …, Fn) и сила R.
Новая система (F1, F2, F3, …, Fn,
R)≡0.
При изучении движения механических систем существенную роль играют не отдельные силы, а
главный вектор и главный момент.
Главным вектором R=f(t,r,V) называют геометрическую сумму всех сил, Fk действующих на
n
отдельные точки механической системы.
R Fk .
k 1
Главный вектор не зависит от выбора системы координат и не зависит от того, к каким
точкам приложены силы.
Главный вектор является причиной поступательного движения тела.
Свойства внутренних сил:
1) главный вектор (геометрическая сумма) всех внутренних сил системы равен нулю
n
R i Fki 0.
k 1
Классификация систем сил:
1. Система сходящихся сил – это совокупность сил линии действия которых пересекаются в
одной точке

5.

Fk z
y
F5
x
Система сходящихся сил всегда имеет равнодействующую, равную
геометрической сумме всех сил системы и приложенную в точке их
пересечения.
F1
F2
Fn
F4
F3
На материальную точку всегда действует система сходящихся сил.
2. Система параллельных сил – это совокупность сил, действующих на твердое тело
линии, действия которых параллельны друг другу.
А) Пространственная система параллельных сил
z
F1
F4
F5
k
Fn i
F3
F2
O
j
x
y
F1
y
F7
F6
Fk
Б) Плоская система параллельных сил
F8
F3
F2
F7
Fn
Fk
j
i
F4
F5
F6
F8
x
O
3. Произвольная система сил – это совокупность сил, действующих на твердое тело линии,
действия которых как угодно расположены в пространстве или плоскости
А) Пространственная система произвольных сил
F4
z
F5
F3
F6
F2
F7
y
O
F1
x
Fn
Fk
Б) Плоская система произвольных сил
y
F5
F4
F3
F6
F2
F7
F8
F1
F8
Fn
O
Fk
x

6.

Сложение сил. Геометрическая сумма (главный вектор) любой системы сил определяется
или последовательным сложением сил по правилу параллелограмма или построением силового
многоугольника.
R F
k
В случае действия на тело двух сил, главный вектор системы находится следующим образом
R F1 F2
F1
Алгебраическая величина главного вектора
в данном случае определяется по теореме
косинусов
R F1 F2 2 F1 F2 cos
F1
R
α
1
1
2
2
F2
F2
В случае действия на теле системы, состоящей из n сил, главный вектор определяется
построением силового многоугольника и равен
F1
R F1 F2 F3 Fk ... Fn
1
F2
F2
F3
F1
2
F3
F4
R
1
F4
Наиболее общим способом сложения сил является аналитический способ, в котором проекции
равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам
проекций этих сил на соответствующие оси:
Rx Fkx , Ry Fky , Rz Fkz .
Модуль равнодействующей и направляющие косинусы равны:
Ry
R
R
R Rx2 Ry2 Rz2 , cos x, R x , cos y, R
, cos z, R z .
R
R
R

7.

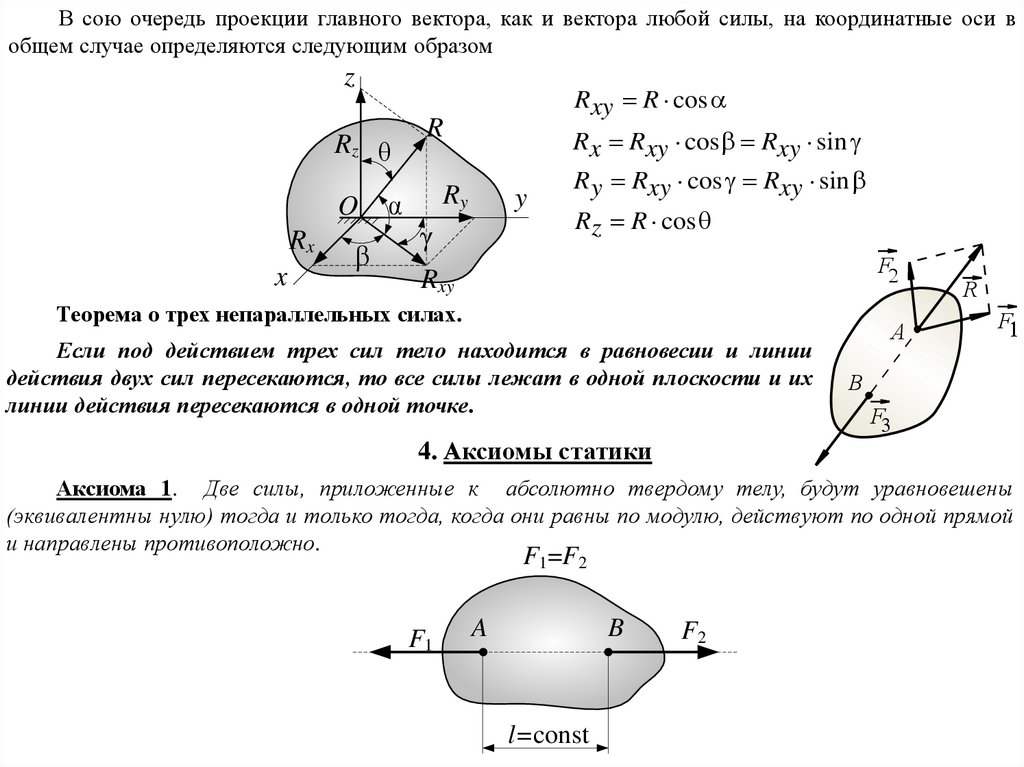
В сою очередь проекции главного вектора, как и вектора любой силы, на координатные оси в
общем случае определяются следующим образом
z
Rz θ
O
Rx
x
β
Rxy R cos
R
Rx Rxy cos Rxy sin
Ry
α
y
γ
R y Rxy cos Rxy sin
Rz R cos
F
Rxy
Теорема о трех непараллельных силах.
Если под действием трех сил тело находится в равновесии и линии
действия двух сил пересекаются, то все силы лежат в одной плоскости и их
линии действия пересекаются в одной точке.
4. Аксиомы статики
А
R
F
B
F
Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены
(эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой
и направлены противоположно.
F1=F2
F1
A
B
l=const
F2

8.

Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или
отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему.
A
F
F1 B F2
A
A F1=F B
Следствие. Не нарушая состояния абсолютно твердого тела, точку приложения силы можно
переносить вдоль линии ее действия, т.е. сила, приложенная к абсолютно твердого тела,
представляет собой скользящий вектор.
Аксиома 3. Не меняя состояния абсолютно твердого тела, две силы, приложенные к одной его
точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их
геометрической сумме (аксиома параллелограмма сил)R=F1+F2, модуль равнодействующей
F1
M
R
α
F2
Следует различать понятия главного вектора (геометрической
суммы всех сил системы) и равнодействующей силы. Например, две
силы F1 и F2, приложенные к телу в точках A и B имеют главный вектор
R, равный геометрической сумме F1 и F2. Но сила R не является
равнодействующей этих сил, так как из рисунка 18 видно, что эта сила R
не может заменить действие сил F1 и F2 на данное тело. Более того
данная система сил не имеет равнодействующей силы.
z
F1
A
B F2
x
R
y

9.

Следствие из аксиомы 3. Только система сил, которую можно привести к равнодействующей
силе R, может иметь уравновешивающую силу Rур
F1
Rур
M
R
α
F2
Аксиома 4. Силы взаимодействия двух тел равны по модулю и направлены по одной прямой
противоположно.
F21
F12 F21
1
F12
2
Силы F12 и F21 не образуют уравновешенной системы сил, так как приложены к разным телам.
Аксиома 5. Равновесие деформируемого (изменяемого) тела не нарушится, если жестко
связать его точки и считать тело абсолютно твердым.