Тема_4

1. Тема 4 Решение систем линейных уравнений

«Вычислительная математика»
Тема 4
Решение систем
линейных уравнений
4.1. Формулы Крамера.
4.2. Метод исключений Гаусса.
4.3. Метод простых итераций.
4.4 Метод прогонки

2.

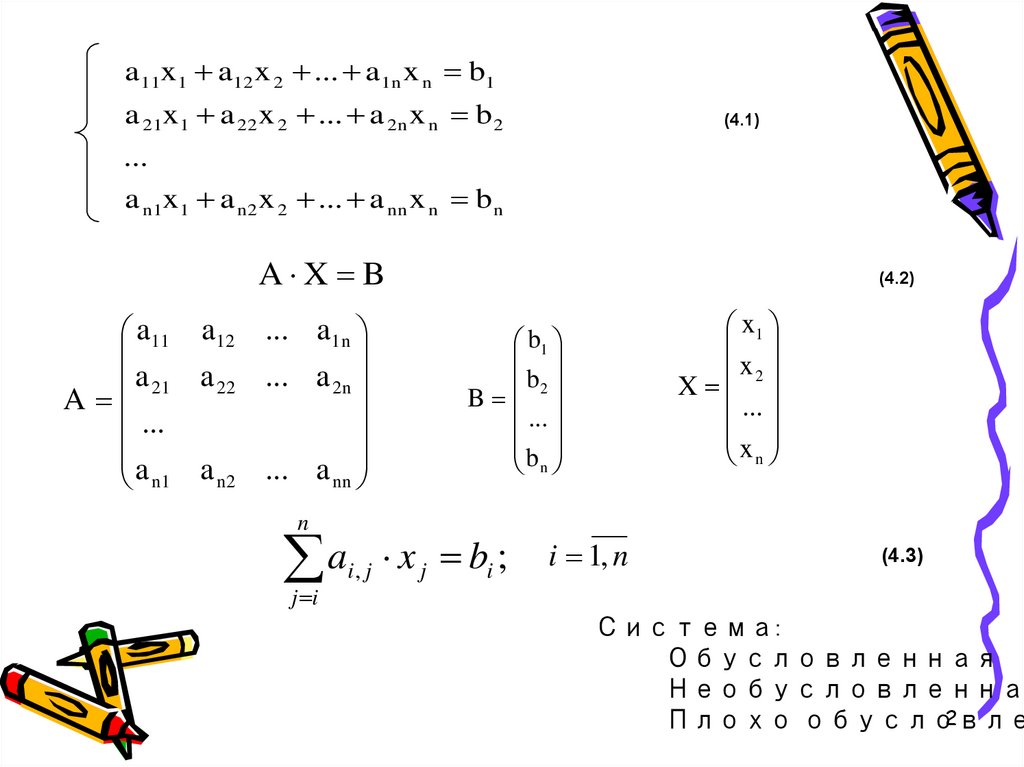
a 11x1 a 12 x 2 ... a 1n x n b1
a 21x1 a 22 x 2 ... a 2n x n b 2
(4.1)
...
a n1x1 a n2 x 2 ... a nn x n b n
A X B
(4.2)
a11 a12 ... a1n
a 21 a 22 ... a 2n
A
...
a
n1 a n2 ... a nn
n
a x b ;
j i
i, j
x1
x2
X
...
x
n
b1
b
B 2
...
b
n
j
i
i 1, n
(4.3)
Система:
Обусловленная
Необусловленная
2
Плохо обусловле

3.

Тип
Прямые
Итерационные
Название метода
Число арифметических действий
(при n = 20)
Область
примененения
Формулы
Крамера
2
n!
n
~
(9,7 1020 )
n<5
(5733)
n<200
2 3
n n2
3
Исключения
Гаусса
~
Простых
итераций
~ n² на каждой итерации (400n)
до 105
Гаусса-Зейделя
t
9,7 10 20
12
30 10
365 24 60 60
1,03
3

4.

4.1. Формулы Крамера.
xi* = i / , i = 1, n, 1
(4.4)
x1 + 5 x2 x3 = 2
x1
2 x3 = -1
2 x1 x2 – 3 x3 = 5
1 5 1
= 1 0
2
2 1 3
1 =
2 5 1
1 0
2
5 1 3
= 0 + 1 + 20 + 0 + 15 + 2 = 38
x1* = 1 / = 38/38 = 1;
x2* = 2 / = 0/38 = 0;
x3* = 3 / =-38/38 = -1.
= 0 + 50 - 1 - 0 + 4 - 15 = 38
2 =
1 2 1
1 1 2
2 5 3
3 =
1 5 2
1 0 1
2 1 5
= 3 + 8 – 5 – 2 + 6 - 10 = 0
= 0 - 10 – 2 – 0 -25 - 1 = -38
4

5.

4.2. Метод исключений Гаусса
x1 + 5 x2 x3 = 2
x1
2 x3 = -1
2 x1 x2 – 3 x3 = 5
1 этап Прямой ход
x1 + 5 x2 x3 = 2
- 5 x2 + 3 x3 = -3
– 38/5 x3 = 38/5
2 этап Обратный ход
x3* = -1
-5 x2 + 3 x3*=-3 x2*=(3 + 3 x3*)=(3 + 3 (-1))=0
x1 +5 x2* - x3*=2 x1*=2 + 5 x2* + x3*=2 + 5 0 + (-1)=1
Контроль правильности решения - рассчет невязок δi
n
i bi a ijx*j i 1, n
j 1
5

6.

Алгоритм прямого хода:
Шаг 1. Примем k=1
Шаг 2. Выбираем рабочую строку.
Если akk ≠ 0, то k-ая строка – рабочая.
Если нет, меняем k-ю строку на m-ю (n≥m>k), в которой amk ≠ 0, .
Если такой строки нет, система вырожденная, решение прекратить.
Шаг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения
коэффициентов.
a ik
qi
a kk
и новые правые части
a ij a ij q i a kj
j k, n
bi bi qi bk
6

7.

Шаг 4. Увеличиваем k = k + 1. Если k = n, прямой ход завершен,
иначе алгоритм повторяется со второго шага.
Получаем верхнюю треугольную матрицу А:
a11 a12 a13 ... a1n
0 a 22 a 23 ... a 2n
A
...
0
0
0 ... a nn
Алгоритм обратного хода:
Шаг 1. Вычислим
b1
b
B 2
...
b
n
bn
x
a nn
*
n
Шаг 2. Вычислим:
n
1
*
xi
(b i
a ij x *j )
a *ii
j i 1
i n 1, n 2,...,1
7

8.

Разновидности метода исключения:
а) Метод исключения Гаусса с выбором главного элемента в столбце
am,k max | a j ,k |
j k ,n
б) Метод Гаусса-Жордана.
i 1, k - 1, k 1, n
прямой ход завершится при достижении условия k>n
a 11 0
0 a 22
A 0
0
...
0
0
0
0
a 33
0
0
... 0
... 0
... a nn
...
xi =bi / aii , i =1,2,…,n
8

9.

4.3. Метод простых итераций.
x1 + 5 x2 x3 = 2
x1
+2 x3 = -1
2 x1 x2 – 3 x3 = 5
4x 1
x2
x3
3
x1
5x 2
x3
2
x1
x2
5x 3
6
1
(3 x 2 x 3 )
4
1
x2
(2 x 1 x 3 )
5
1
x 3 (6 x 1 x 2 )
5
x1
(0)
x 1(0) 0, x (0)
2 0, x 3 0
x 1(1)
1
3
(0)
(3 x (0)
x
)
0,75
2
3
4
4
1
2
(2 x 1(0) x 3(0) )
0,4
5
5
1
6
x 3(1) (6 x 1(0) x (0)
1,2
2 )
5
5
x (1)
2
(0)
(1)
(0)
δ max x i(1) x i(0) max x1(1) x1(0) , x (1)
max 0,75;0,4;1 ,2 1,2
2 x2 , x3 x3
i 1,3
δ>ε
9

10.

1
1
4,6
(1)
(3 x (1)
x
)
(
3
0
,
4
1
,
2
)
1,15
2
3
4
4
4
1
1
0,05
(1)
(1)
x (2)
(2
x
x
)
(
2
0
,
75
1
,
2
)
0,01
2
1
3
5
5
5
1
1
5,65
x 3(2) (6 x1(1) x (1)
)
(6
0,75
0,4)
1,13
2
5
5
5
x1(2)
δ max x i(2) x i(1) max | 1,15 - 0,75 |; | 0,01 - 0,4 |; | -1,13 1,2 | 0,4
i 1,3
1
4,14
(3 0,01 1,13)
1,0350
4
4
1
0,28
x (3)
(2
1
,
15
1
,
13
)
0,056
2
5
5
1
4,86
x 3(3) (6 1,15 0,01)
0,972
5
5
x 1(3)
(4)
x 1(4) 1,007, x (4)
2 0,0014, x 3 0,9818,
δ 0,158
δ 0,0546
10

11.

Основные расчетные зависимости метода простых итераций:
Формула итерационного процесса:
x
(k)
i
n
1
(b i a ij x (kj 1) )
a ii
j 1
i 1, n
i j
Условия завершения итерационного процесса
max x i(k) x i(k 1)
i 1,n
1 n (k)
x i x i(k 1)
n i 1
Условие сходимости итерационного процесса
n
a ii a ij
i 1, n
j 1
i j
11

12.

4.4 Метод Гаусса-Зейделя
i 1
n
1
X i( k )
(bi ai , j x kj ai , j x kj 1 ),
ai ,i
j 1
j 1 1
n
1
xi
(bi ai , j x j ),
ai ,i
j 1
i 1, n
i 1, n
i j
12