Элементы статики

1. Лекция 8 Элементы статики

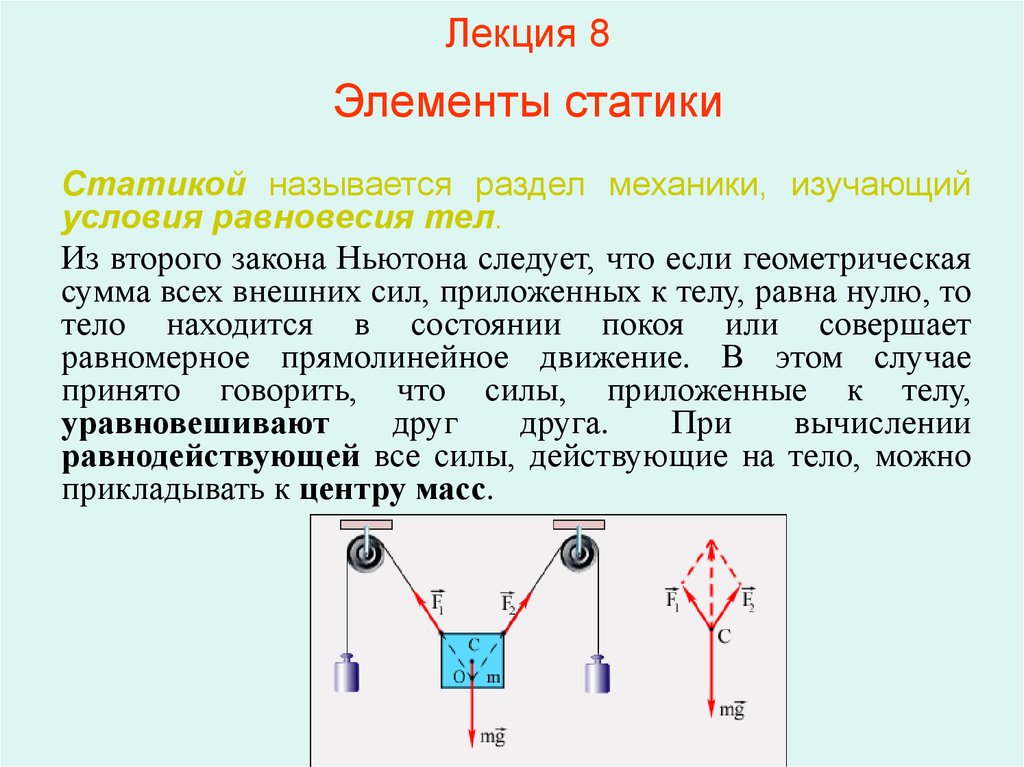
Статикой называется раздел механики, изучающий
условия равновесия тел.
Из второго закона Ньютона следует, что если геометрическая
сумма всех внешних сил, приложенных к телу, равна нулю, то
тело находится в состоянии покоя или совершает
равномерное прямолинейное движение. В этом случае
принято говорить, что силы, приложенные к телу,
уравновешивают
друг
друга.
При
вычислении
равнодействующей все силы, действующие на тело, можно
прикладывать к центру масс.

2. В общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение двух условий: равенство нулю ра

В общем случае, когда тело может двигаться поступательно и вращаться,
для равновесия необходимо выполнение двух условий: равенство нулю
равнодействующей силы и равенство нулю суммы всех моментов.
Оба эти условия не являются достаточными для покоя.
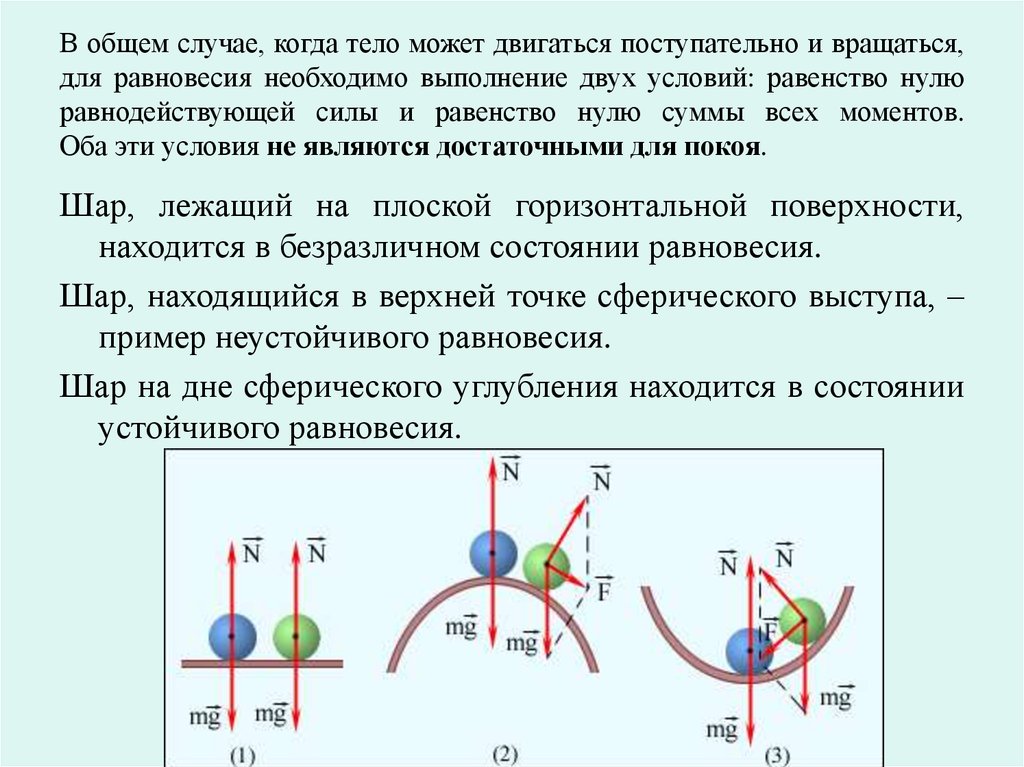
Шар, лежащий на плоской горизонтальной поверхности,
находится в безразличном состоянии равновесия.
Шар, находящийся в верхней точке сферического выступа, –
пример неустойчивого равновесия.
Шар на дне сферического углубления находится в состоянии
устойчивого равновесия.

3. Особым случаем равновесия является равновесие тела на опоре.

Особым случаем равновесия
равновесие тела на опоре.
является
Тело находится в равновесии, если вертикальная линия,
проведенная через центр масс тела, проходит через
площадь опоры

4. Механические колебания

1. Свободные механические колебания.
1.1. Пружинный маятник
1.2. Физический маятник
1.3.Математический маятник
1.4. Графическое представление колебаний
2.Затухающие колебания
3. Вынужденные колебания

5. 1. Свободные механические колебания

Линейный гармонический осциллятор – колебательная система,
совершающая собственные колебания по гармоническому закону
Примеры линейных гармонических осцилляторов
Пружинный маятник – материальная точка массой m, подвешенная на
пружине жесткостью k.
Физический маятник – абсолютно твердое тело, способное совершать
колебания вокруг неподвижной точки, не совпадающей с его центром
инерции.
Математический маятник – материальная точка, подвешенная на
невесомой и нерастяжимой нити длиной l.
Гармонические колебания линейного гармонического осциллятора
можно представить так: вторая производная от смещения по времени
должна быть прямо пропорциональна величине смещения из
положения равновесия
r r 0

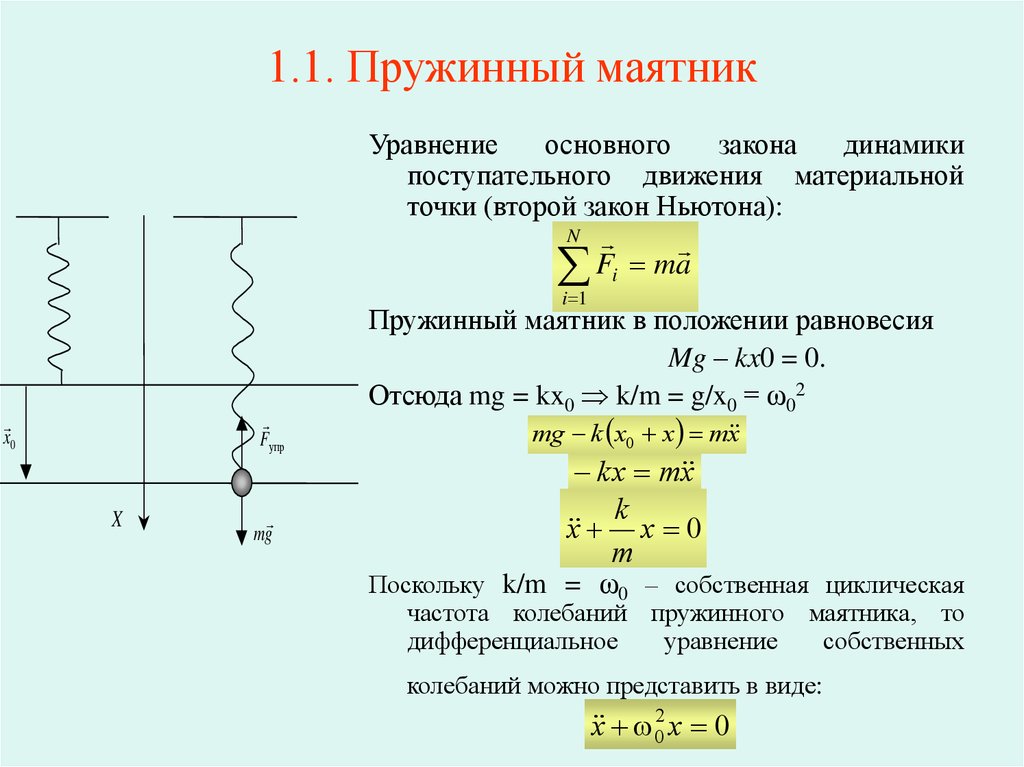
6. 1.1. Пружинный маятник

Уравнение
основного
закона
динамики
поступательного движения материальной
точки (второй закон Ньютона):
Fi ma
N
i 1
Fупр
x0
X
mg
Пружинный маятник в положении равновесия
Mg – kx0 = 0.
Отсюда mg = kx0 k/m = g/x0 = ω02
mg k x0 x m x
kx m x
k
x x 0
m
Поскольку k/m = ω0 – собственная циклическая
частота колебаний пружинного маятника, то
дифференциальное
уравнение
собственных
колебаний можно представить в виде:
x 02 x 0

7.

Собственная циклическая (круговая) частота
0 2 0
2
T0
зависит от параметров колебательной системы:
k
0
m
Если в начальный момент времени t = 0 смещение x0 = xm, то
φ = π/2 и решение интегрального уравнения имеет вид:
x t xm sin 0t
2
Период собственных колебаний: T0.
Линейная частота: 0.
Фаза колебания: Ф = 0t + φ определяет значение смещения х
в данный момент времени, где – начальная фаза
колебания.
Уравнение гармонических колебаний пружинного маятника:
k
x t хm cos
t
m

8. 1.2. Физический маятник

Динамика физического маятника: M – вектор момента силы тяжести относительно точки
О; О – точка подвеса, θ – вектор угла поворота; С – центр инерции dθ/dt – угловая
скорость.
Уравнение основного закона динамики вращательного
N
абсолютно твердого тела:
M i ф , mg
движения
i 1
d 2
ф mg sin 2
dt
При малых углах sin (в радианах). Тогда:
d 2
ф mg 2
dt

9.

Дифференциальное
уравнение
колебаний физического маятника:
ф mg
собственных
ф mg
0
0
Поскольку
– собственная циклическая
частота колебаний, то дифференциальное уравнение
собственных колебаний физического маятника:
2 0
0
– момент инерции маятника относительно точки О,
h – высота, на которую поднимается центр инерции
(точка С), определяется по формуле:
h ф 1 cos
здесь lф = ОС – длина физического
маятника, а - hm
максимальная высота подъема центра инерции.
При малых θ sin (в радианах) и тогда
2
cos 1 sin 1 1
2
2
2

10.

Поэтому
hm
ф
2
m
2
и
h
ф
2
,
2
где
θ - мгновенное значение угла отклонения маятника от
положения равновесия, а θm - максимальное значение этого
угла.
Уравнение гармонических колебаний физического маятника:
t m sin 0t
2
Амплитуда θm определяется начальным запасом энергии и не
зависит от параметров колебательной системы.
2
0 2 0
Собственная циклическая (круговая) частота
T0
зависит от параметров колебательной системы:
mg ф
0
Период собственных колебаний: T0.
Линейная частота: 0.
Фаза колебания: Ф = 0t + φ определяет значение смещения в
данный момент времени.
Уравнение гармонических колебаний физического маятника:
mg ф
t m cos
t

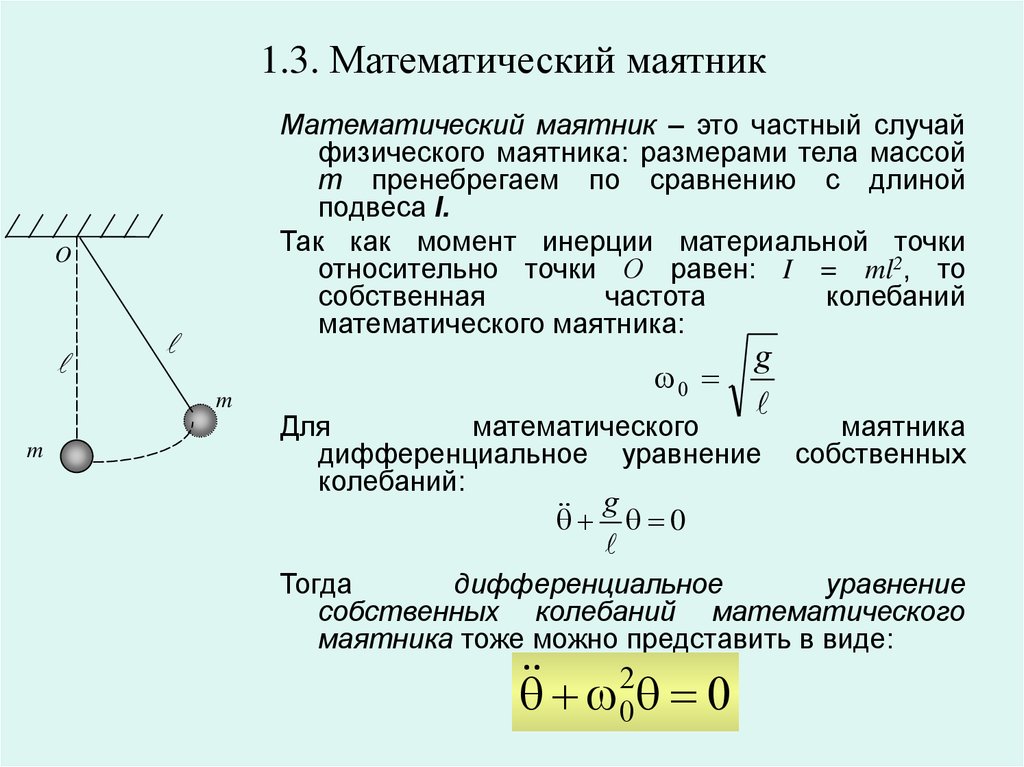
11. 1.3. Математический маятник

Математический маятник – это частный случай
физического маятника: размерами тела массой
m пренебрегаем по сравнению с длиной
подвеса l.
Так как момент инерции материальной точки
относительно точки О равен: I = ml2, то
собственная
частота
колебаний
математического маятника:
O
m
m
0
g
Для
математического
дифференциальное уравнение
колебаний:
маятника
собственных
g 0
Тогда
дифференциальное
уравнение
собственных колебаний математического
маятника тоже можно представить в виде:
2 0
0

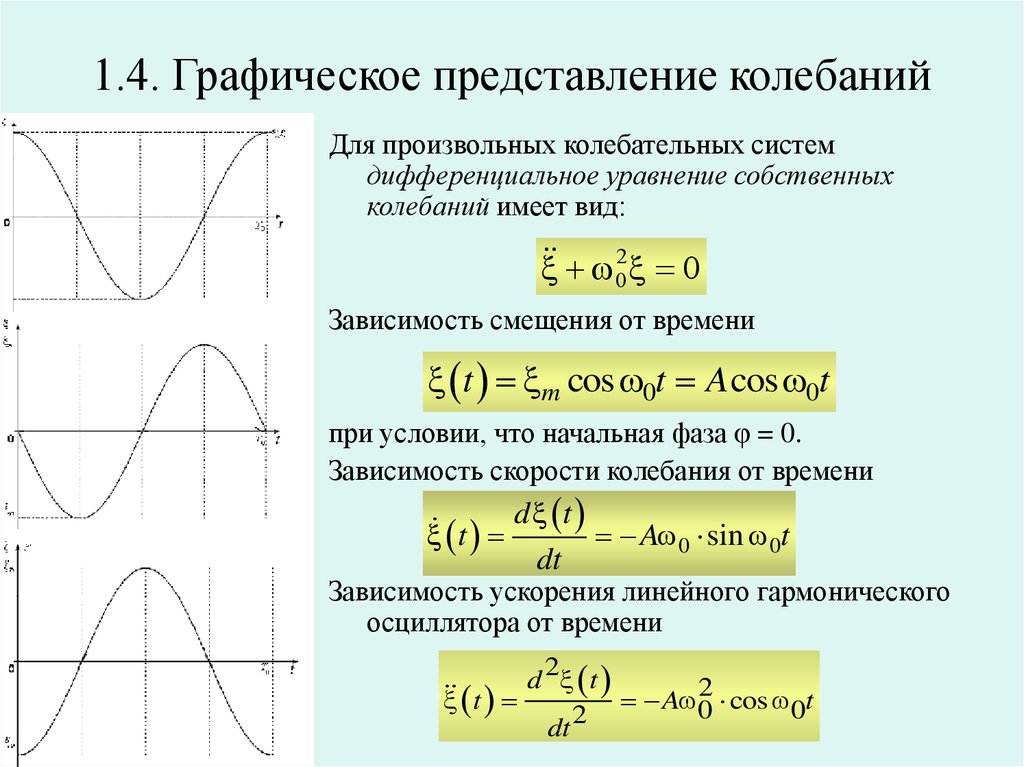
12. 1.4. Графическое представление колебаний

Для произвольных колебательных систем
дифференциальное уравнение собственных
колебаний имеет вид:
2 0
0
Зависимость смещения от времени
t m cos 0t A cos 0t
при условии, что начальная фаза φ = 0.
Зависимость скорости колебания от времени
t
d t
dt
A 0 sin 0t
Зависимость ускорения линейного гармонического
осциллятора от времени
d 2 t
2 cos t
t
A 0
0
dt 2

13. 2. Затухающие колебания

Второй закон Ньютона для пружинного маятника в вязкой среде:
kx rx m x
где rx – сила вязкого трения; r – коэффициент трения.
Тогда дифференциальное уравнение затухающих колебаний пружинного
маятника:
m x rx kx 0
или
x 2 x 02 x 0
Здесь β = r/2m – коэффициент затухания.
Для произвольных колебательных систем дифференциальное уравнение
затухающих колебаний имеет вид:
2 2 0 ,
0
а его решение
A t cos t ,
где
2
02 2
T
– частота затухающих колебаний;
T – период затухающих колебаний.
A t A0e
t

14.

A0
0
t
T'
-A 0
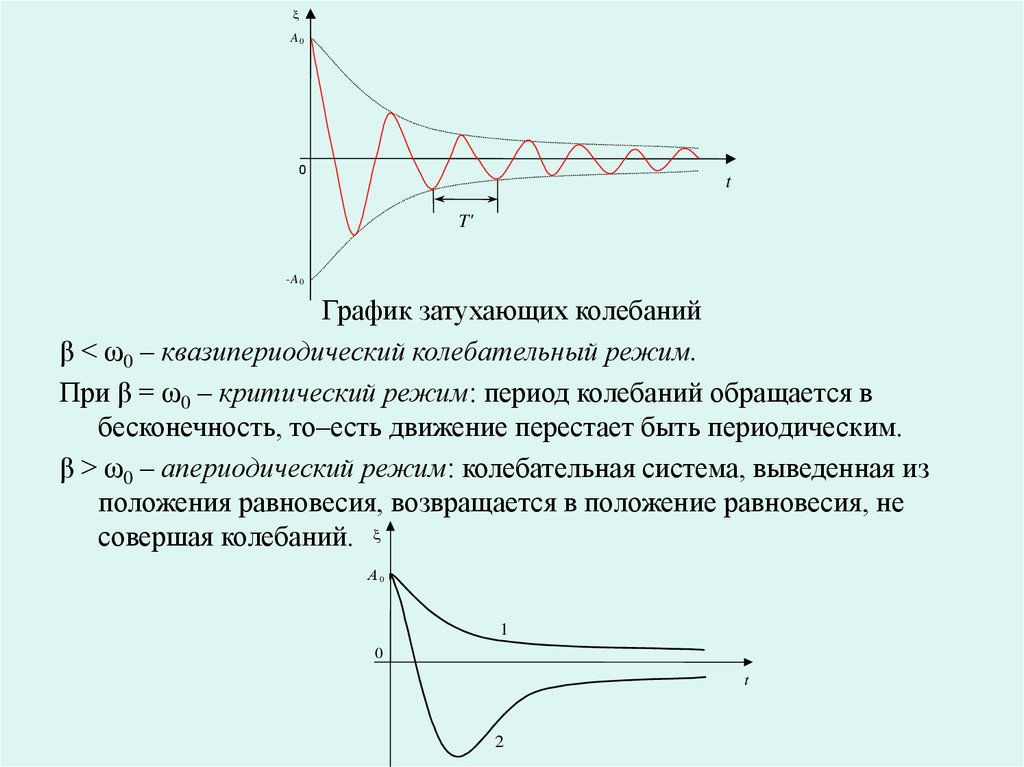
График затухающих колебаний
β < ω0 – квазипериодический колебательный режим.
При β = ω0 – критический режим: период колебаний обращается в
бесконечность, то–есть движение перестает быть периодическим.
β > ω0 – апериодический режим: колебательная система, выведенная из
положения равновесия, возвращается в положение равновесия, не
совершая колебаний.
А0
1
0
t
2

15. Параметры затухающих колебаний

Коэффициент затухания β
Если за некоторое время e амплитуда колебаний уменьшается в e раз
A 0
,
то
Тогда
A 0
A 0 e
e e
e
e
e
e
A e
.
, а, следовательно,
1
e
,
где e – время релаксации.
Логарифмический декремент затухания λ
Логарифмический декремент равен натуральному логарифму отношения
амплитуд соседних колебаний, то есть отличающихся на один период
t
T :
1
1
A t
A 0 e
T
T
ln
ln
T
e
Ne
t T
A t T
A 0 e
Физический смысл логарифмического декремента – величина, обратная
числу колебаний, в течение которых амплитуда убывает в e раз:
e
Ne
T

16. 3. Вынужденные колебания

Вынужденными колебаниями называются колебания, происходящие под
действием внешней переменной (периодической) силы, работа
которой компенсирует потери энергии на преодоление трения (в
механических колебательных системах) и на преодоление
электрического сопротивления (в электрических колебательных
N
системах).
F
m
a
В соответствии со вторым законом Ньютона:
,
i
i 1
Fупр Fтр F ma
,
где
F F0 cos t – внешняя периодическая сила, действующая на
пружинный маятник.
В скалярном виде:
kx rx F0 cos t m x.
Дифференциальное уравнение вынужденных колебаний пружинного
маятника:
F
r
k
x x x 0 cos t
можно представить в виде
m
m
m
,
2
x 2 x 0 x f 0 cos t
где
f0
F0
m
– приведенная сила.

17.

В колебательной системе одновременно происходят два процесса:
1. Затухающие колебания x1(t);
2. Незатухающие вынужденные колебания x2(t) с частотой вынуждающей
силы.
Решение дифференциального уравнения вынужденных колебаний
представим в виде суммы двух решений x = x1 + x2:
Общее решение однородного уравнения затухающих колебаний:
x1 t A0 e t cos t ,
где 02 2 – циклическая частота затухающих колебаний.
Уравнение справедливо, если
2
f0
tg
2 2 при < и
и
A
0
A
2
0
2
2
0
4 2 2
f0
tg
2
2 02
при > 0.
Резонансом называют явление резкого увеличения амплитуды
вынужденных колебаний при приближении частоты вынуждающей
силы к частоте собственных колебаний ( 0).
Функция A( ) достигает экстремума при частоте вынуждающей силы ,
равной
рез 02 2 2
,
здесь
рез
–
резонансная частота.
2
2 02
4 2 2
и

18.

f0
F0
A 2
2
0 m 0 m k
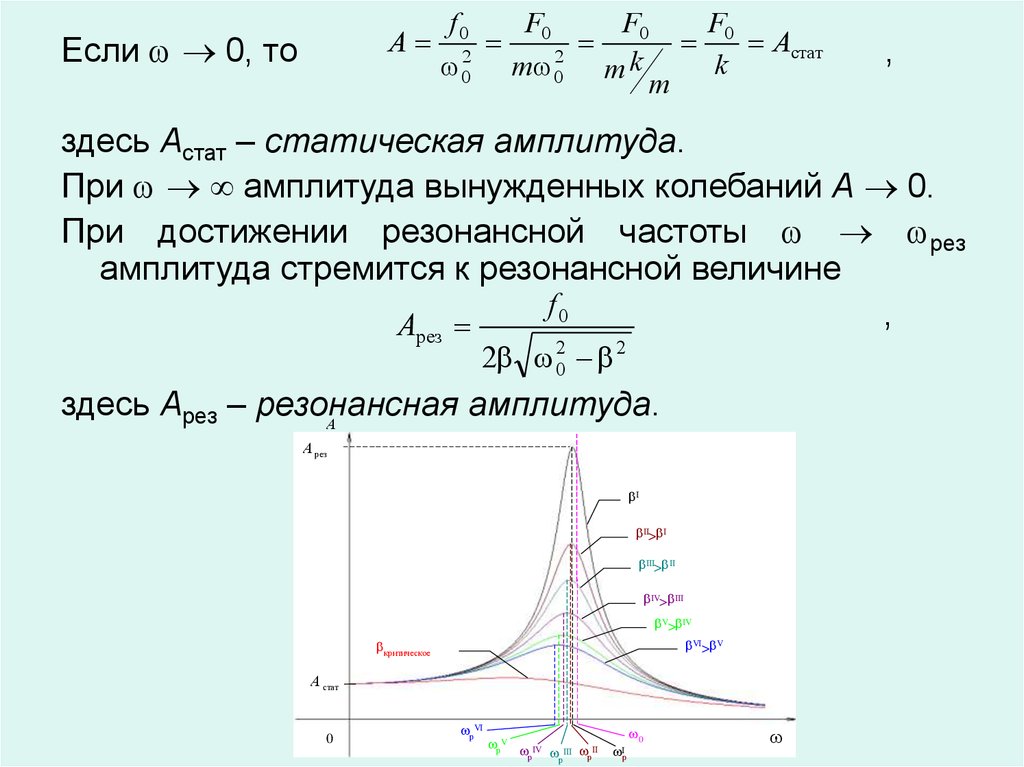
Если 0, то
F0
m
F0
Aстат
k
,
здесь Aстат – статическая амплитуда.
При амплитуда вынужденных колебаний A 0.
При достижении резонансной частоты рез
амплитуда стремится к резонансной величине
f0
,
A
рез
2 02 2
здесь Aрез – резонансная
амплитуда.
А
А рез
I
II> I
III> II
IV> III
V> IV
VI > V
критическое
А стат
0
рVI
рV
рIV III рII
р
Iр
0

19. Добротность колебательной системы, находящейся в режиме вынужденных колебаний, можно найти как , где 0,7 – ширина резонансной кривой на

Добротность колебательной системы, находящейся в
режиме вынужденных колебаний, можно найти как
рез
Q
, где 0,7 – ширина резонансной кривой
0,7
на уровне половинной мощности внешнего источника
Aрез
вынуждающей силы
0,7 Aрез
.
2
Добротность Q определяется как величина,
логарифмическому декременту затухания:
обратно
0,7
A
A рез
0,7 Арез
A стат
0
рез
пропорциональная
Q Ne
2
.
При слабом затухании добротность можно представить как
Q 2
E0
E
,
где Е0 – запасенная энергия; E – потери энергии за один период.
Добротность можно представить и как отношение резонансной амплитуды к
статической, т.е. как коэффициент усиления:
Aрез
Q
Aстат .
При слабом затухании добротность равна
.
Q 0
2