лекция -ориентирование линии (1)

1.

ОРИЕНТИРОВАНИЕ НА МЕСТНОСТИ
Ориентирование линии –
Это определение ее направления на местности
или плане относительно другого направления,
принятого за исходное.
Ориентирование производится относительно северных направлений
магнитного, географического или осевого меридианов.

2.

В каждой зоне осевой меридиан - это прямая линия в натуральную
величину.
Остальные меридианы зоны изображаются кривыми линиями.
Кривизна их увеличивается по мере удаления
от осевого меридиана.
Экватор изображается прямой линией.

3.

Ориентирование по географическому меридиану
Географический азимут (истинный) –
это горизонтальный угол, отсчитываемый по часовой стрелке
от северного направления географического меридиана
до направления линии.

4.

Азимуты А1, А2, А3 не равны между собой.
Так, А2 и А3 отличаются от А1 на величину
сближения меридианов γ :
А2 = А1 – γзап,
А3 = А1 + γвост .
На картах указывается сближение меридианов

5.

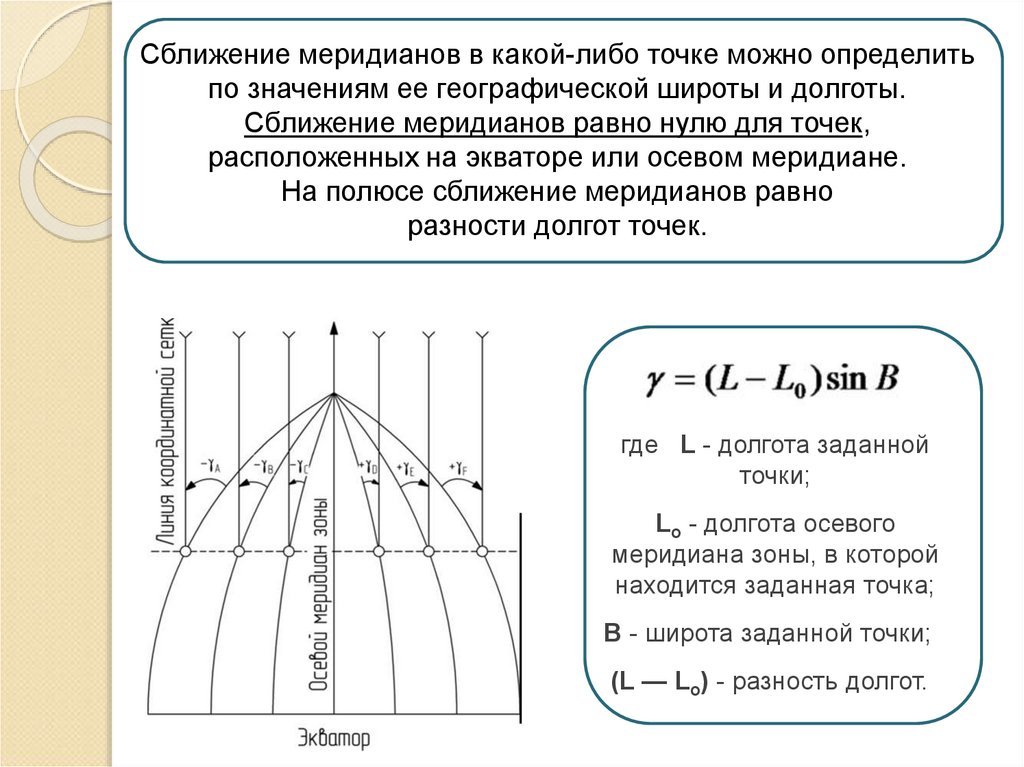
Сближение меридианов в какой-либо точке можно определить
по значениям ее географической широты и долготы.
Сближение меридианов равно нулю для точек,
расположенных на экваторе или осевом меридиане.
На полюсе сближение меридианов равно
разности долгот точек.
где L - долгота заданной
точки;
Lo - долгота осевого
меридиана зоны, в которой
находится заданная точка;
В - широта заданной точки;
(L — Lo) - разность долгот.

6.

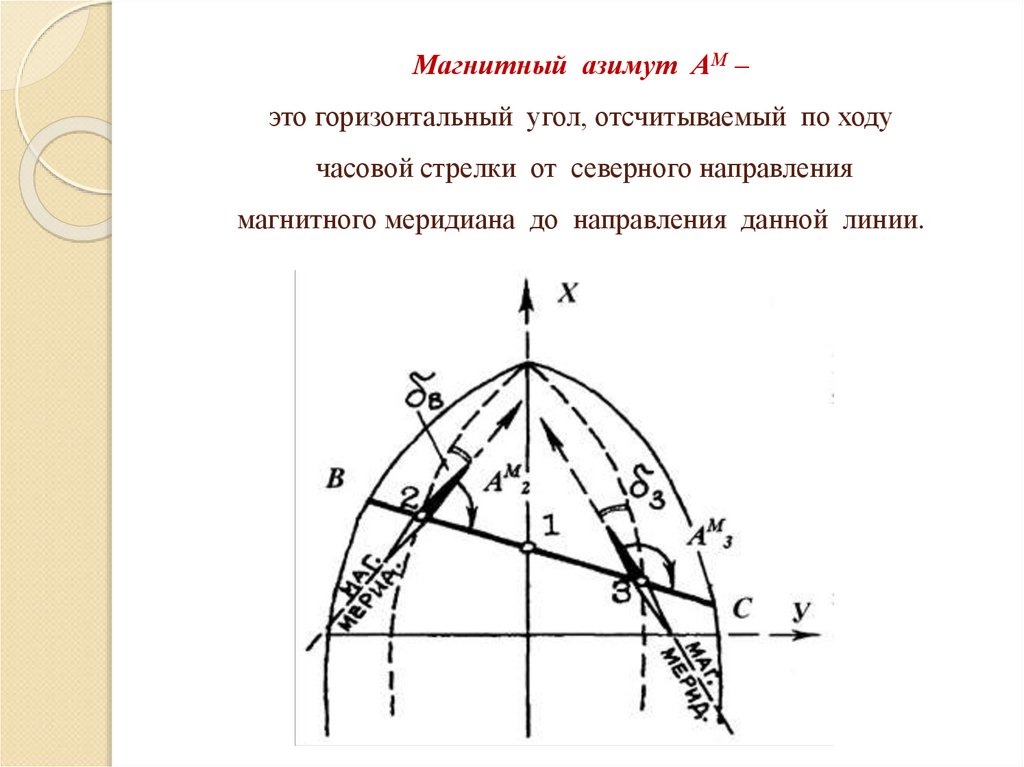
Магнитный азимут АМ –
это горизонтальный угол, отсчитываемый по ходу
часовой стрелки от северного направления
магнитного меридиана до направления данной линии.

7.

Угол между истинным и магнитным меридианами называется
склонением магнитной стрелки δ , отсюда:
А2 = АМ2 + δвост ,
А3 = АМ3 – δзап .
На территории страны δ колеблется от 0о до ±15о .

8.

Дирекционный угол - горизонтальный угол α ,
отсчитываемый по ходу часовой стрелки от
северного направления осевого меридиана зоны (оси абсцисс Х)
или параллельной ему линии до направления данной линии.

9.

Дирекционные углы, определенные в одном направлении линии
называют прямыми αАВ – прямой дирекционный угол направления АВ,
αВА - обратный дирекционный угол направления ВА
Прямой и обратный дирекционные углы
отличаются друг от друга на 180°.
αВА = αАВ +180о
αАВ
αВА

10.

В отличие от азимутов дирекционный угол линии
в любой её точке сохраняет свою величину.
Дирекционные углы и азимуты изменяются от 0о до 360о .

11.

Румбом называется острый горизонтальный угол r,
отсчитываемый от ближайшего (северного или южного)
направления оси Х (или параллельной ей линии)
до направления данной линии.
Румбы могут изменяться только в пределах от 0о до 90о.
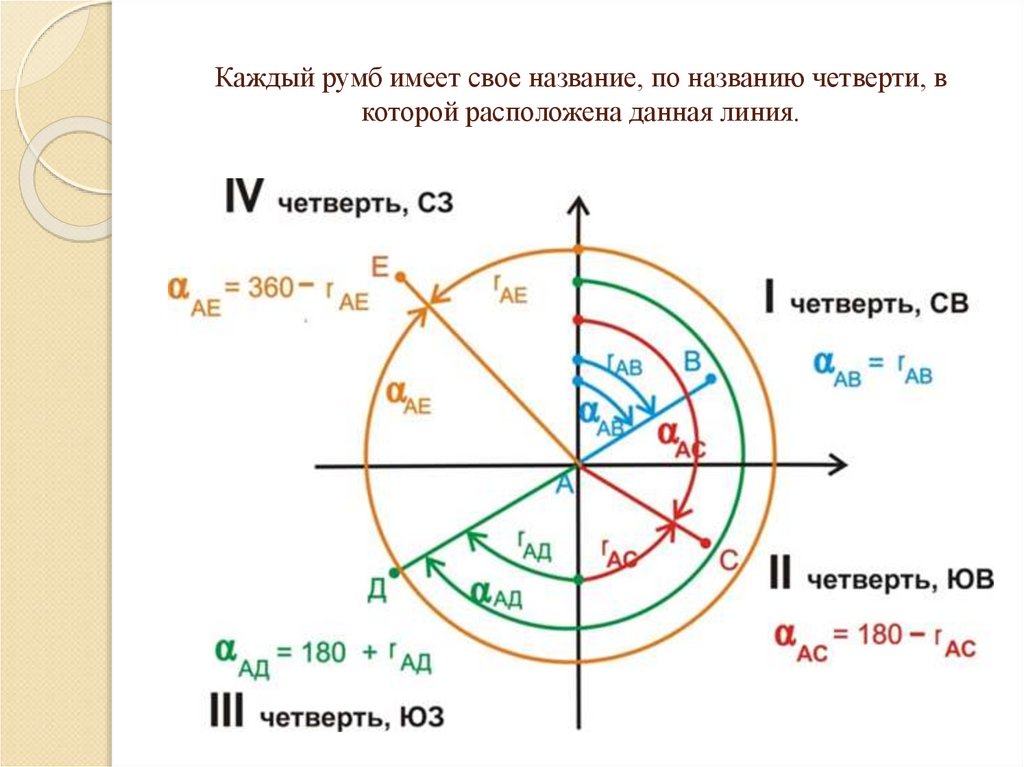
Каждый румб имеет свое название, по названию четверти, в которой
расположена данная линия.

12.

Связь между дирекционными углами α и румбами r
00 < α <900
r1 = α
α

13.

Связь между дирекционными углами α и румбами r
900 < α <1800
r2 = 1800 – α
α

14.

Связь между дирекционными углами α и румбами r
1800 < α < 2700
r3 = α – 1800
α

15.

Связь между дирекционными углами α и румбами r
2700 < α < 3600
r4 = 3600 – α
α

16.

Каждый румб имеет свое название, по названию четверти, в
которой расположена данная линия.

17.

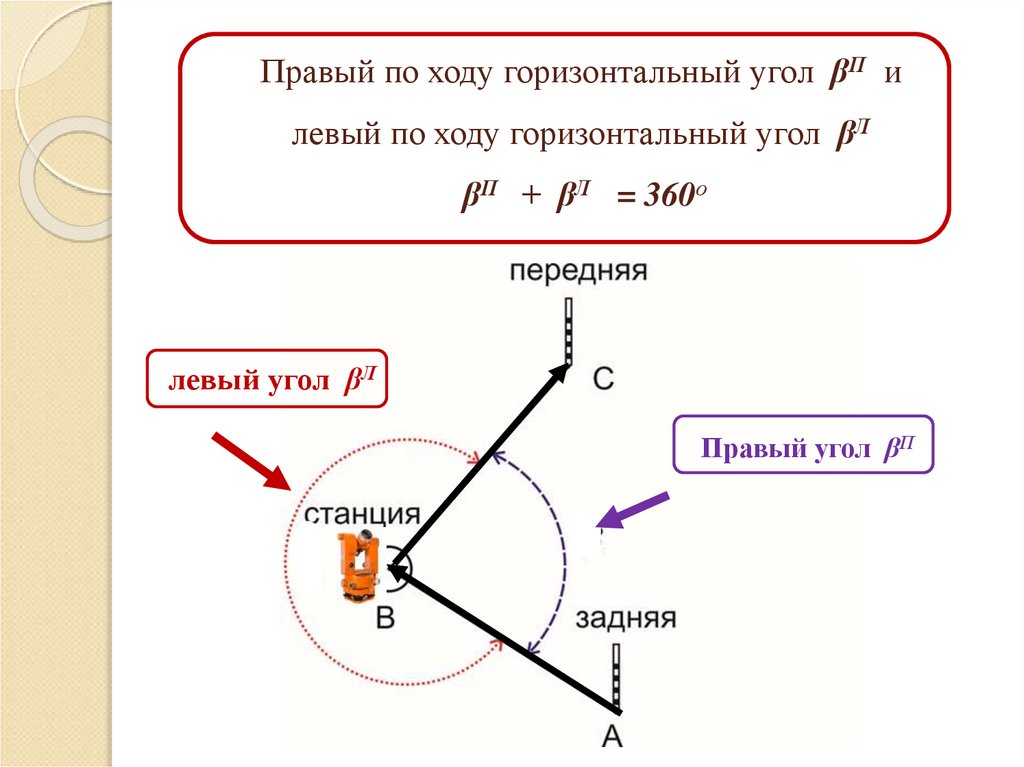
Правый по ходу горизонтальный угол βП и
левый по ходу горизонтальный угол βЛ
βП + βЛ = 360о
левый угол βЛ
Правый угол βП

18.

Связь между дирекционными углами
предыдущей и последующей сторон.
Задача - по известному дирекционному углу α1-2 стороны 1–2
вычислить дирекционный угол α2-3 стороны 2–3 , если известен
βП2 или βЛ2 (правый или левый) угол между этими сторонами.

19.

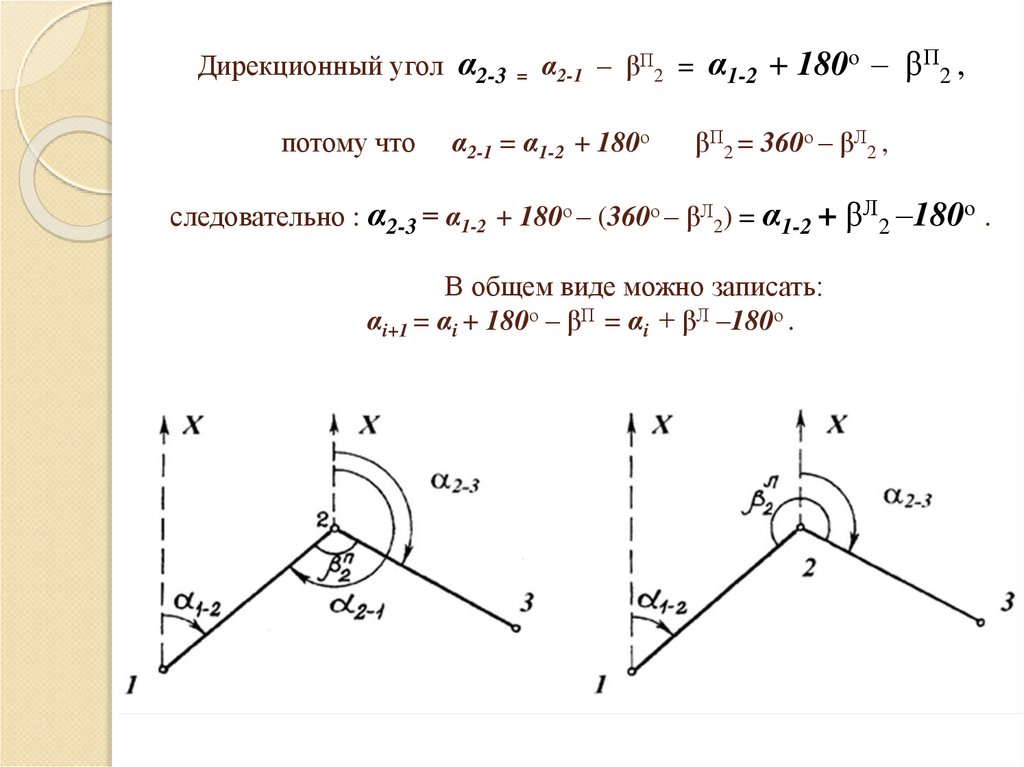
Дирекционный угол α2-3 = α2-1 – βП2 = α1-2 + 180о – βП2 ,
потому что
α2-1 = α1-2 + 180о
βП2 = 360о – βЛ2 ,
следовательно : α2-3 = α1-2 + 180о – (360о – βЛ2) = α1-2 + βЛ2 –180о .
В общем виде можно записать:
αi+1 = αi + 180о – βП = αi + βЛ –180о .

20.

Знаки координат абсциссы Х и ордината У
имеют такие же знаки как и в прямоугольной системе:
абсциссы к северу от экватора положительные, к югу –
отрицательные; ординаты на восток от осевого меридиана
положительные, на запад – отрицательные.

21.

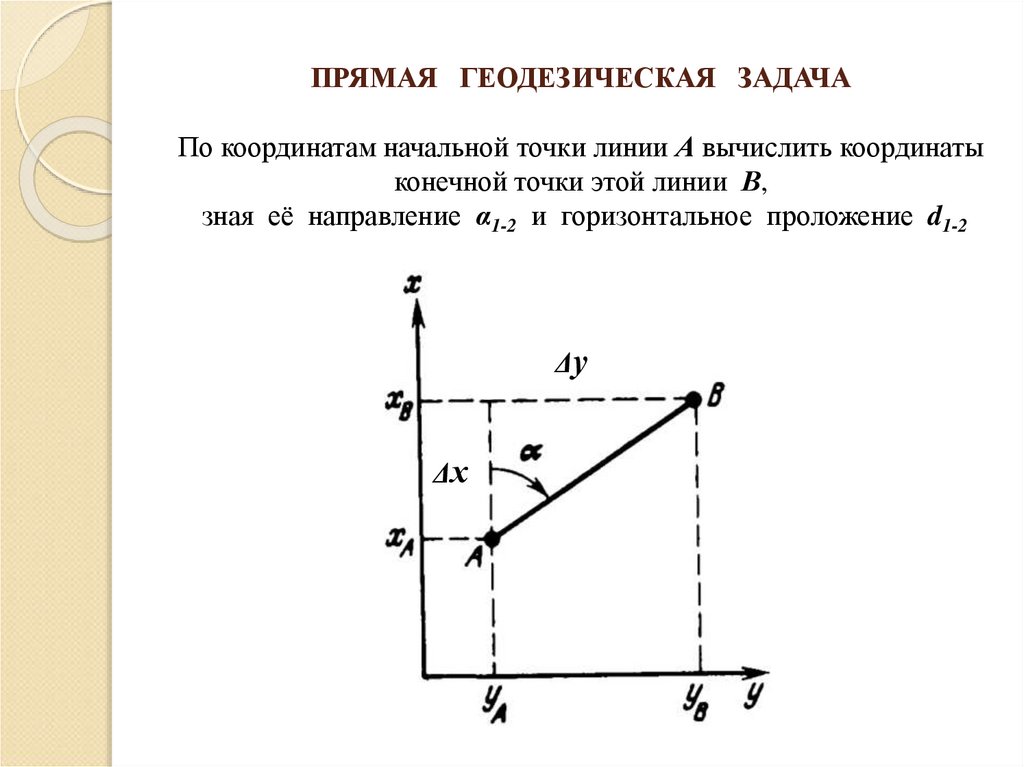
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
По координатам начальной точки линии А вычислить координаты
конечной точки этой линии В,
зная её направление α1-2 и горизонтальное проложение d1-2
Δу
Δх

22.

ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
По координатам начальной точки линии 1 вычислить координаты
конечной точки этой линии 2 ,
зная её направление α1-2 и горизонтальное проложение d1-2 .

23.

Дано: Х1 , У1 , α1-2 , d1-2 .
Найти: Х2 , У2 .
Из решения прямоугольного треугольника (заштрихован)
вычисляем приращения координат Δх1-2 и Δу1-2 :

24.

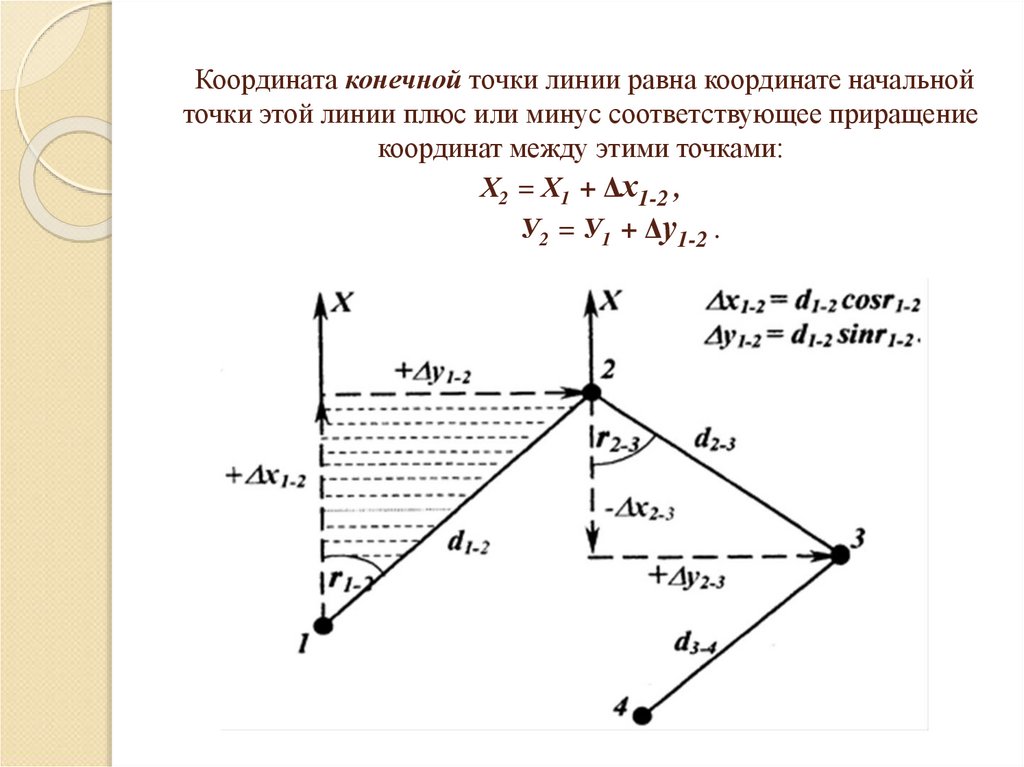
Координата конечной точки линии равна координате начальной
точки этой линии плюс или минус соответствующее приращение
координат между этими точками:
Х2 = Х1 + Δх1-2 ,
У2 = У1 + Δу1-2 .

25.

Зная координаты точки 2 , можно вычислить координаты
точки 3, если известен дирекционный угол α2-3 , горизонтальный
угол βП2 горизонтальное проложение d2-3.

26.

Знаки приращений координат зависят от названия румба.
Так, если румб стороны 1–2 имеет название СВ,
то и Δх1-2 и Δу1-2 будут со знаком «плюс».
Для стороны 2–3 (ЮВ) знаки приращений –Δх2-3 и +Δу2-3.
Для стороны 3–4 (ЮЗ) оба приращения со знаком «минус».
Для стороны 4–1 (СЗ) имеем +Δх4-1 и –Δу4-1 .

27.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
По известным координатам начальной 1 и конечной 2 точек линии
вычислить её направление α1-2 и горизонтальное проложение d1-2
1. Вычисляют приращения координат стороны 1–2, вычитая из
координат конечной точки 2 координаты начальной точки 1:
Δх1-2 = Х2 – Х1 ,
Δу1-2= У2 – У1 .
2. По знакам приращений координат определяют название румба,
а по отношению Δу/Δх = tgr1-2 находят значение румба.
3. По величине и названию (знаку) румба находят
дирекционный угол α1-2 данной линии.
4. Вычисляют величину горизонтального проложения :
d1-2 = Δх/cos r
или
d1-2 = Δу/sin r
По обеим формулам должны получить два абсолютно одинаковых
значения , что является контролем решения
обратной геодезической задачи.